铁电薄膜平均极化性质的理论研究

董亚男，张 芹

近些年来，薄膜制备技术有了突飞猛进的发展，这也吸引着许多物理学者的目光，进而对人工复合铁电双层膜、多层膜以及超晶格进行了更加深入的研究，因此铁电薄膜渐渐深入到微电子等诸多领域中。至今，理论与实验研究者已经对铁电双层膜以及多层膜的居里温度、介电常数以及自发极化等诸多的物理性质都进行了的研究。

一、模型与理论

迄今为止，铁电薄膜的结构变得更加多样化，我们要研究的铁电双层膜具有这样的特点：（1）具有表面过渡层；（2）夹持在两个标准的金属平行板电极之间；（3）构成薄膜的两层铁电材料是完全不同的，第一层的厚度为L1，第二层的厚度为L2，所以我们得到双层膜的总厚度是L=L1+L2，如图1。

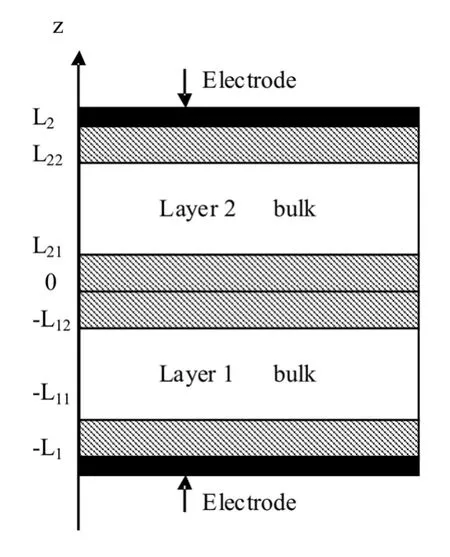
图1 含有界面耦合过渡层的铁电双层膜的几何结构

现在我们假设铁电层1和2均是具有二级相变的铁电材料且均处于单畴的状态，铁电材料层1和2的极化强度分别为P1和P2而且它们的极化方向都垂直于薄膜表面并且都沿着图1中z轴的正方向。在与薄膜表面平行的平面内1层和2层薄膜的极化性质都是均匀的，但自发极化和薄膜表面垂直的方向，即z轴方向上不是均匀的，是发生变化的。

由于铁电材料层1和2之间过渡层的存在引起了在垂直于薄膜的z方向上体系的极化分布具有不均匀性。当体系的状态处于非均匀时，它的自由能密度以及自发极化必定是位置的函数。由于构成铁电双层膜的两种铁电材料都具有二级相变，所以铁电双层膜单位面积的总的自由能密度能表示成：

其中，F1是铁电层1的自由能密度；F2是铁电层2自由能的密度；Fint是间界层的自由能密度。

铁电层1的自由能密度F1可以表示成：

式中A1，B1，C1和K1都是正值，均是自由能展开式的系数，而且和坐标轴z以及温度T均无关；T01是铁电层1体材料的相变温度；E1是铁电层1的外电场，方向沿着z轴正方向；ψ1（z）是描述铁电层1表面过渡层的影响。

为了使P1（z）和它的微商能够具有连续性，必须满足以下边界条件：

其中，-L11是铁电层1下表面过渡层的边界位置；-L12是铁电层上表面过渡层的边界位置。

与此相同，F2作为铁电层2的自由能密度能够表示成：

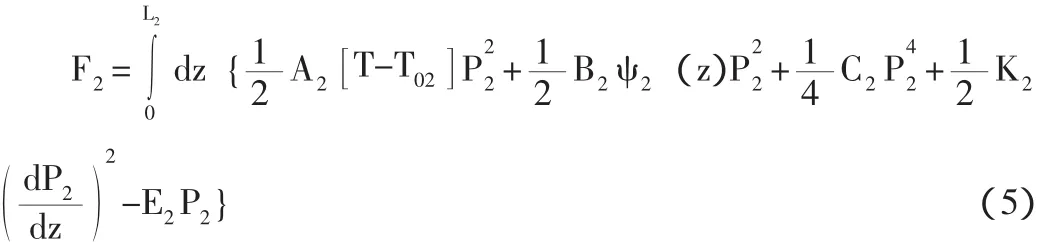
其中，A2，B2，C2和K2都是正值，为自由能展开式的系数，而且和坐标轴z以及温度T均无关；T02是铁电层2的体材料的相变温度；E2是铁电层2的外电场，它的方向沿着z轴正方向；ψ2（z）是铁电层2表面过渡层的作用。同理，为了使P2（z）和其微商具有连续性，应该满足以下边界条件：

其中，L21是铁电层2的下表面过渡层边界位置；L22是铁电层2的上表面过度层边界位置。

界面能的自由能可以表示成：

其中，P1（0）表示当z=0时，铁电层1的极化强度；P2（0）表示当z=0时，铁电层2的极化强度；J是假定的界面耦合常数。当耦合支持铁电相时J＞0；当耦合支持反铁电相时J＜0。在这里我们只研究J＞0的情况，即铁电相。按照热力学假设，当体系处于热平衡的状态时，当P1、P2变化时，它的总自由能将会取到最小值δF=0。

此时的Euler-Lagrange方程是：

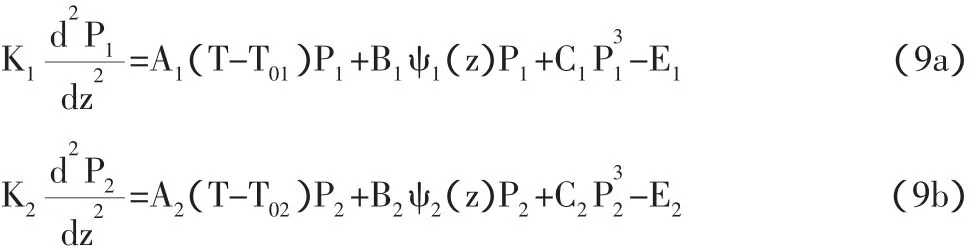
与其对应的边界条件是：

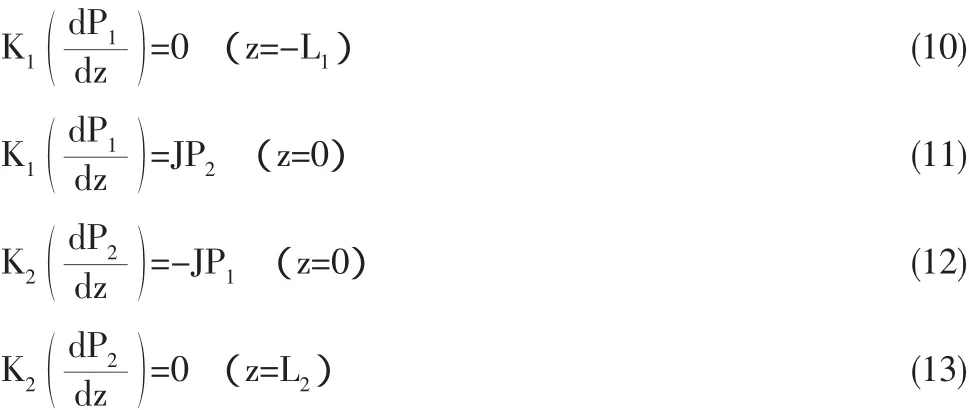
为了方便起见，我们将这里的物理量约化成无量纲的形式。即令为真空介电常数），i=1，2。我们可以充分地利用这些参数将方程（9a）与（9b）变成如下形式：

参数σi（i=1，2）是与其对应的铁电体材料的居里常数C与居里温度T0的比值，即。当为二级铁电相变时，居里常数的数量级是103K，居里温度的数量级是102K，所以在计算时我们取σi=6，并且假定铁电层1的相变温度比铁电层2的相变温度要大，此时γ＞1。

ψ1（ζ）代表在连续的铁电层1内部自发极化的分布函数；ψ2（ζ）代表在连续的铁电层2内部自发极化的分布函数。将它们的形式选取为：

此时选取的分布函数ψ1（ζ）与ψ2（ζ）的形式仍然具有普遍性。

其中，l1i=L1i/ξ0，l2i=L2i/ξ0（i=1，2）；参数λ11（λ12）是铁电层1的上表面或下表面附近自由能密度随着位置的变化情况；参数λ21（λ22）——铁电层2的上表面或下表面附近自由能密度随着位置的变化情况。

方便起见，我们将两个铁电层中的过渡层均假定是对称的，则满足下列情况：

ls=2（l1-l11）=2l12=2l21=2（l2-l22），ls是每一个铁电层中过渡层的厚度。

将体系的平均自发极化f以及体系的平均极化率χf定义成：

其中，l=l1+l2是铁电双层膜总的厚度。

二、数值计算与讨论

1.一定温度下平均极化随参量α的变化。图2给出了一定温度时，平均极化随参量α的变化曲线。从图中我们可以看到，当参量α增大时，体系的平均极化明显增加。产生这一现象的原因是由于当参量α增大时，两个铁电层之间的界面耦合也将增加，因此导致铁电双层膜中平均极化的增大。

2.一定温度下平均极化与参量γ的变化。图3计算了一定温度下，体系的平均极化随参量γ的变化。由图中曲线可以清楚地看到，随着参量γ的增加，铁电双层膜的平均极化减小。当γ取较小值时，铁电双层膜的平均极化减小的幅度非常显著，而在γ取较大值时，平均极化随参量γ的变化并不明显。由此我们可以得知，当γ较大时，即两种不同材料铁电层的相变温度的差异较大时，参量γ对铁电双层膜的平均极化影响较小。

3.一定温度下平均极化随界面耦合系数的变化。图4描述了一定温度下，体系的平均极化与参量的变化关系。由图3、4中曲线可以得知，当增加界面耦合系数的值时，体系的平均极化有明显的增加，而且平均极化随界面耦合系数的变化接近于线性变化。由此我们可以推断出，界面耦合增强时，有利于铁电体处于铁电相。

图2 一定温度下平均极化随的变化

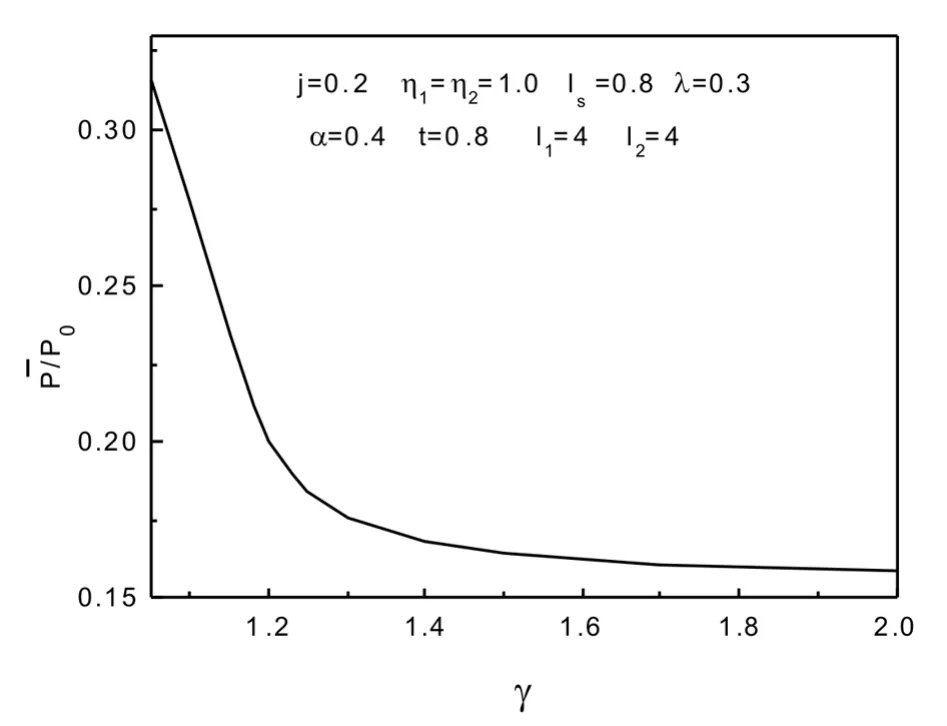
图3 一定温度下平均极化随的变化

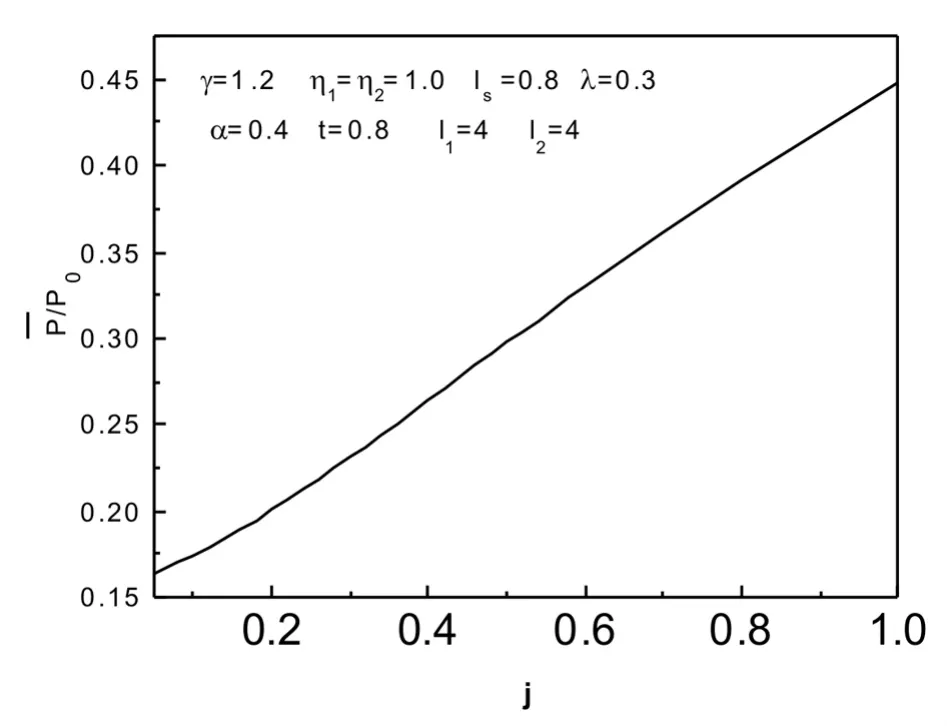
图4 一定温度下平均极化随界面耦合系数的变化

4.一定温度下平均极化随双层膜厚度的变化。固定温度，计算了平均极化随铁电双层膜厚度的变化曲线。从图5中曲线我们可以看到，随着铁电双层膜厚度的增加，平均极化明显的增加。这一现象可以解释为，当铁电双层膜厚度增加时，由于表面过渡层的厚度是固定的，所以表面过渡层相对于薄膜的相对厚度减小，这样就使得体系的平均极化有所提升。

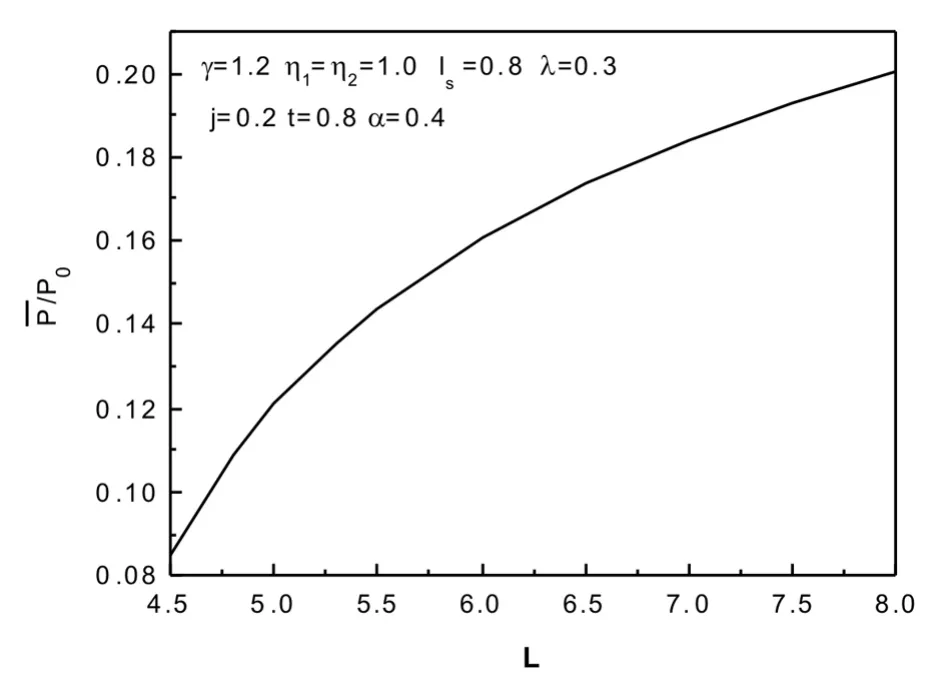
图5 一定温度下平均极化随双层膜厚度的变化

三、结论

1.描述两种铁电薄膜物性差异的参量对铁电双层膜的平均极化性质的影响很大。

2.当温度一定时，铁电双层膜的平均极化随着参量、界面耦合系数以及双层膜的厚度L的增大而增大，两个铁电层之间的界面耦合也将增加，有利于铁电体处于铁电相。

3.当温度一定时，铁电双层膜的平均极化随着参量的增大而减小，当较大时，参量对铁电双层膜的平均极化影响较小。

[1]TILLEY D R.Landau theory for coupled ferromagnetic and ferroelectric films and supper lattices[J].Solid State Communications，1988，（65）：657-660

[2]SARKAR A，RANJITH R，KRUPANIDHI S B.Nonlinear dielectric behavior in three-component ferroelectric supper lattices[J].Journal of Applied Physics，2007，（102）

[3]STARKOV A S，PPAKHOMOV O V.Influence of the dynamic polarization of a ferroelectric material on the magnitude of its electro caloric response[J].Technical Physics letters，2010，36（1）：3-9

[4]Guo Yiping，Daisuke Akai，Kzauaki Sawada.Structure and electrical properties of trilayered/thin films deposited on Si substrate[J].Solid State Communications，2009，（149）：14-17

[5]Zhong S，Alpay S P，Cole M W.Highly tunable and temperature insensitive multilayer barium strontium titanate films[J].Applied Physics Letters，2007，（90）