基于压缩感知的道路交通参数修复方法研究

徐东伟,董宏辉,李海舰,贾利民*

(北京交通大学a.轨道交通控制与安全国家重点实验室；b.交通运输学院,北京100044)

基于压缩感知的道路交通参数修复方法研究

徐东伟a,b,董宏辉a,b,李海舰a,b,贾利民*a,b

(北京交通大学a.轨道交通控制与安全国家重点实验室；b.交通运输学院,北京100044)

为了解决交通路网中的道路交通检测器大面积发生故障时道路交通参数数据的缺失或异常问题,本文提出了一种基于压缩感知的道路交通参数修复方法.首先对道路交通参数矩阵进行分解和逼近;然后在道路交通参数矩阵进行分解和逼近的基础上,利用压缩感知的理论及方法进行道路交通参数修复,并对基于压缩感知进行道路交通参数修复的过程中所涉及的主要参数进行分析和设定;最后依据实例对基于压缩感知的道路交通参数数据修复算法进行验证.选取北京市典型快速路对该算法进行验证,结果证明,基于压缩感知的道路交通参数数据的修复方法具有高精度,在实际应用中是可行的.

智能交通;交通参数修复;压缩感知;道路交通;数据修复

1 引 言

交通运输作为现代经济的重要部分,承担着客货物运输、公共基础设施服务,是人们出行的必要内容.但是伴随着社会经济的发展,道路交通需求与交通能力供给的矛盾日益凸显,交通拥堵、交通事故等交通问题日益突出.为了解决这些交通问题,提高城市交通系统的运行效率、改善城市的交通运行状况,智能交通系统(Intelligent Transportation System,ITS)是最为有效的途径之一.而道路交通路网上的交通状态信息的实时准确获取是建设智能交通系统和进行道路交通管理的基础,在交通系统运行管理控制中起着基础性和关键性的作用.道路交通参数的获取方法是改善城市交通安全、提升交通运行效率和产业发展的核心问题.

但是由于交通检测器硬件故障、噪声干扰、通讯故障以及外界环境带来的影响等因素,往往导致异常数据和丢失数据的发生.针对这些情况,既有的道路交通参数数据修复方法主要可以分为以下两种情形:

(1)空间序列数据缺失处理.若一个或某几个不连续地点的检测数据缺失,则可以采用相邻地点的检测数据进行估计[1]；若连续几个地点的检测数据缺失,则必须根据历史数据进行估计.

(2)时间序列数据缺失处理.当大批量的数据缺失时,可采用上一周同一天的历史数据或多个周的同一天历史数据的加权估计值进行修补；当仅有几组数据出现故障时,可采用相邻时段数据的平均值进行修复,也可采用交通参数预测方法对缺失数据进行补充[2].

但是当交通路网中的道路交通检测器大面积发生故障时,仍然缺乏有效的道路交通参数的修复方法.由于道路交通在时间和空间上具有流动的特性,空间序列下游的道路交通参数是上游的道路交通参数在时间轴上的延续流动[3],因此道路交通参数数据在时间和空间上具有强烈的相关特性,因此道路交通参数数据具有一定的结构特性.而道路交通参数数据的结构特性导致了其具有可压缩性和冗余性.因此,在道路交通网络中大面积的道路交通参数数据不可用时,可以利用道路交通参数数据的潜在结构特征,通过压缩感知的方法、利用可用的道路交通参数数据来恢复故障道路交通参数数据.

2 压缩感知理论简介

近年来,由D.Donoho、E.Candes及T.Tao等人提出了压缩感知(Compressive Sensing)理论:对可压缩的信息可通过远低于采样定理的方式采集信息,仍能够以高精度恢复出原始信息,实现恢复重建[4].压缩感知的过程如图1所示.压缩感知理论在采集信息的过程中进行数据压缩,其采样频率远低于采样定理的频率,可实现高分辨率信号的采集.其突出优点是集合了传统采样过程中的数据采集和数据压缩,从而极大地提高了数据传输效率,降低了数据存储空间.

图1 压缩感知过程Fig.1 The process of compressive sensing

在图1中 X∈RN,为原始信号集；y∈RM,为观测值信号集；∈RN,为重构值信号集；M≪N.y和X具有如下关系:

式中 Φ为大小为M×N的感知矩阵,该矩阵与信号集互不相关.

由图1中,我们可以看出,压缩感知主要包括压缩感知和稀疏重建两个关键过程:

(1)压缩感知.

压缩感知理论的前提是原始信号集X具有可压缩性.当原始信号集X具有可压缩性时,其通过正交稀疏变换

式中 Ψ为稀疏矩阵；S为稀疏信号(S只有K个非零元素).

故压缩感知的测量过程为

式中 Θ=ΦΨ,为观测过程矩阵,该矩阵需要满足有限等距性条件(Restricted Isometry Property).

E.Candes等给出了有限等距性条件的具体内容和证明[5].对于任意K阶稀疏信号C和常数δk∈(0,1),如果矩阵Θ满足:式中 ‖C‖l2为矩阵C的l2范数.则称矩阵Θ满足有限等距性.

(2)稀疏重建.

由于测量信号y的维数M远远小于原始信号X的维数N(即所谓的欠采样情况),故利用极不完整的测量信号y恢复出完整的原始信号X为一欠定问题.根据压缩感知理论,利用极少的测量信号y也有可能实现对原始信号X的较好恢复.该恢复过程可用下式表达:

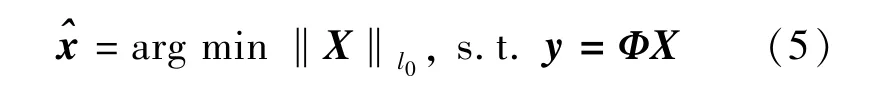
式中 ‖X‖l0为原始信号集X的l0范数.但上式是一个典型的N-P难问题,数值计算极不稳定.文献[4]中,Donoho将l0范数由l1范数替代,并证明该方法在信号X具有稀疏性以及X和Φ互不相关的前提下能获得同等的解.故将上式进行如下变化:

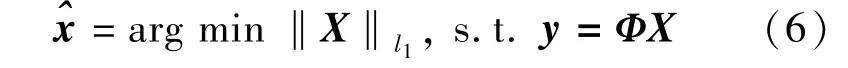
该问题为一凸优化问题,解决该问题的过程即是利用凸优化理论解决稀疏信号的重构.这个过程需要通过一定的稀疏重建策略,寻求最稀疏解.

3 基于压缩感知的道路交通参数修复算法

根据文献[6]中对道路交通参数矩阵的分析可知,道路交通参数矩阵存在潜在的结构特性,故道路交通参数矩阵具有很强的可压缩性,因此利用压缩感知获取道路交通参数是可行的.

3.1 道路交通参数数据矩阵的分解和逼近

设定交通状态数据的采集周期是Δt,选取的时间长度为(m·Δt),选取的交通路网的路段共有n条.定义路段i(1＜i＜n,i∈N*)在时刻(t,t+ Δt)的统计交通状态值为xr,t,则我们可以得到一个交通状态矩阵(xr,t)m×n,记为X.其中,路段i与路段i+1为相邻路段.

矩阵的SVD分解是进行矩阵可压缩性分析的基础性工作.对于任意一个m×n阶矩阵X,都可以分解为三个矩阵,形如:

式中 VT为矩阵V的转置；U为m×m的酉矩阵；V为n×n的酉矩阵,Σ是半正定m×n阶对角矩阵, Σ对角线上的元素σi即为矩阵X的奇异值(i=1, 2,…,r),r为矩阵X的秩.通常将值σi由大及小进行排列,即σi＞σi+1.

通过对道路交通参数矩阵的奇异值分解,我们可以得到:

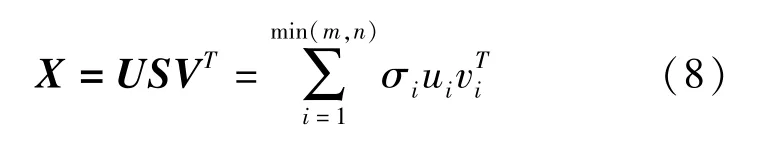
式中 ui和vi分别是矩阵U和V的第i列.矩阵X的特征值由σi表征.

选取前r个奇异值,从而可以得到对原始交通状态矩阵X的一个近似逼近矩阵:

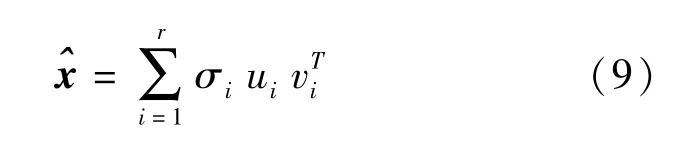
式中 r≪min(m,n).

3.2 基于压缩感知的道路交通参数修复方法

根据道路交通参数矩阵的分解和逼近,假设选取的确定特征流对应的奇异值的个数为r,则对原始交通状态矩阵X的近似逼近矩阵为

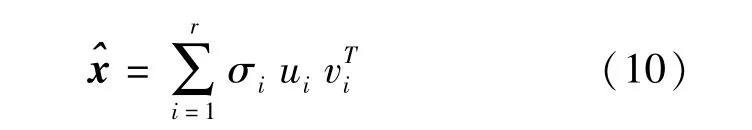
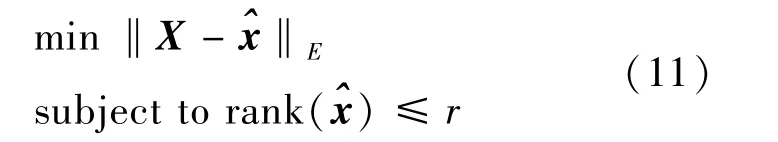
但在实际逼近原始道路交通参数矩阵的过程中,我们无法得到原始交通状态矩阵,我们只能得到相关的道路交通参数测量矩阵M.对M有如下定义:

式中 M和B均为大小为m×n的矩阵.B为观测矩阵,其定义如下:

道路交通参数矩阵具有潜在的结构特性和可压缩特性,故近似逼近矩阵映射到原始交通矩阵的低维子空间,近似道路交通参数矩阵应该存在一个较小的秩.因此可以通过下面的模型进行求解:

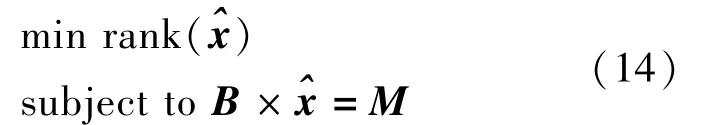
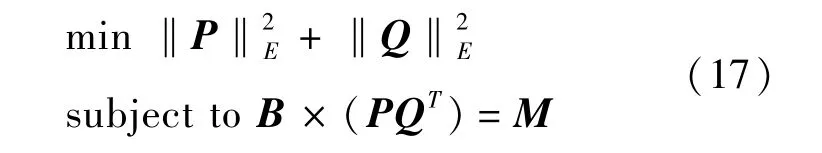
但是,由于道路交通参数矩阵的秩在近似逼近的条件下才较小,而且道路交通参数矩阵往往含有测量误差,所以难以完全满足测量等式B×(PQT) =M.因此借鉴文献[8]中对该种问题的处理,我们引入参数λ,得到如下模型:

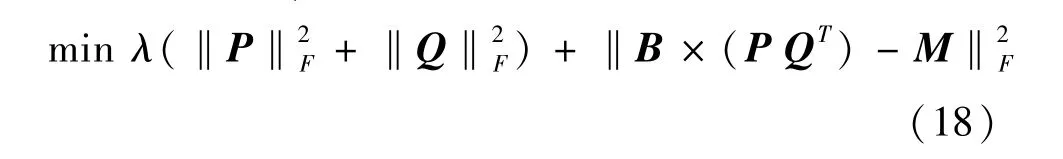
式中 P和Q分别为m×r和n×r的矩阵.

因此有如下模型:

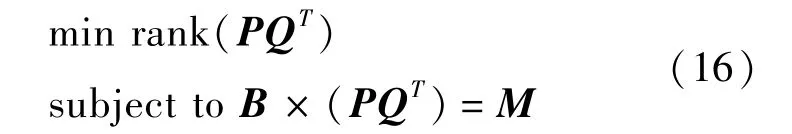
但是上述模型是非凸的目标优化问题,难以进行求解.在满足有限等距性条件(Restricted Isometry Property)且矩阵具有较小的秩时,文献[7]提出了通过对矩阵的范数最小化可以得到与对矩阵秩的最小化同等的解.因此,我们可以利用更为简单的模型对上述模型进行求解:

该模型在考虑满足测量等式的同时,也考虑了交通状态矩阵的向低维空间逼近的特性.通过参数λ的调节,还可以实现两者对逼近精度的调节.

对于矩阵P和Q的求解可通过最小二乘法实现.首先,获取一个随机矩阵作为P的初始值,固定P,然后通过最小二乘法求解当下P对应的最优的Q；然后固定Q,通过最小二乘法求解当下Q对应的最优的P；然后一直循环寻找P和Q的最优解.当算法收敛时,即可获得最优的P和Q.

但是由于大量的循环计算使得算法的计算负荷度较高.故设定每获得一组局部最优的P和Q时,计为一次循环,设定第h次循环时的目标值为:

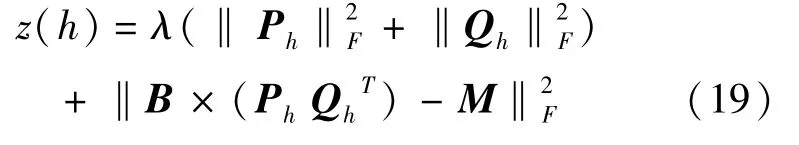
式中 Ph和Qh分别对应第h次循环时P和Q的最优值.根据实际的道路交通状态获取精度的需求,设定一个阈值yset,当|z(h)-z(h-1)|≤yset时, Ph和Qh即为全局最优的P和Q,从而最终获得对原始矩阵的近似逼近矩阵.

但是近似逼近矩阵在逼近实际的道路交通参数矩阵时,还存在一定的残差,故获取的最优逼近矩阵应为

式中 E为大小为m×r的残差矩阵.

3.3 相关参数设定方法

在基于压缩感知的道路交通参数获取的过程中,涉及到的参数主要包括近似逼近矩阵的秩r和引入的参数λ.针对不同时间和空间上的道路交通参数矩阵,获取最优的相似逼近矩阵时对应的r和λ各不相同.这里所做的参数设定只是对参数对基于压缩感知的道路交通参数获取算法的大概影响分析.

由于两个参数对算法的精度各有影响,单独分析每个参数对算法精度的影响并不能确保算法的最优,因此在进行算法分析时应该同时考虑r和λ对该道路交通参数获取算法的影响.

引入归一化平均绝对误差(Normalized Mean Absolute Error,NMAE)[8]对参数对算法精度的影响进行分析.

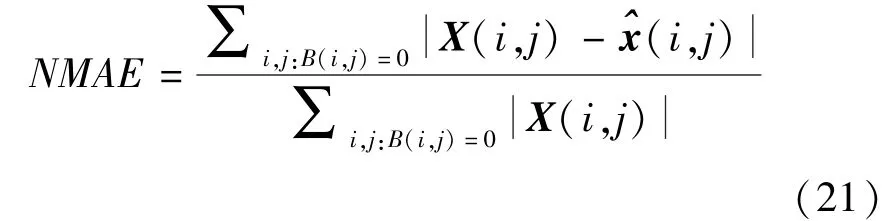
即对于不同的(r,λ),存在与之对应的NMAE.故存在如下等式:

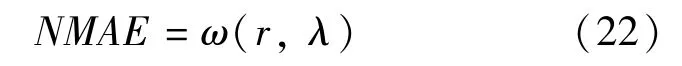
即(r,λ)与NMAE存在某种分布关系ω,寻找NMAE最小时对应的(r,λ),即为最优参数设定过程.最终(r,λ)的取值可以通过历史道路交通参数数据的统计分析确定.

3.4 残差矩阵确定方法

在同一道路交通运行模态下,残差矩阵的取值基本一致.故残差矩阵可以通过历史道路交通参数数据的统计分析获得.残差矩阵的确定过程主要包含以下步骤:

(1)提取历史道路交通参数数据,获得一个历史道路交通参数矩阵,记为Xh(mh×nh),并利用SVD分解进行处理:

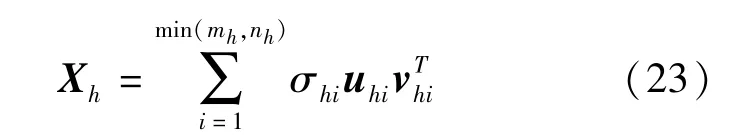
(2)在不同的道路交通参数数据缺失率下,r的取值各不相同.故初始残差矩阵Eh通过下式获得:

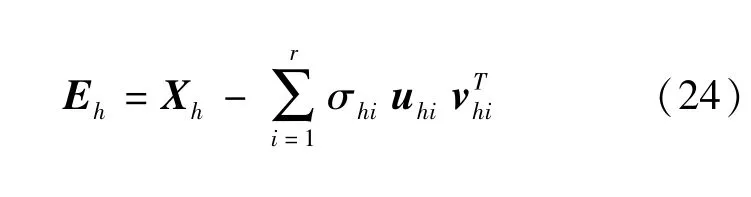
(3)基于历史交通状态数据获取的残差矩阵中,包含历史道路交通运行状态的部分突变信息,因此需要对初始残差矩阵进行平滑滤波处理,从而获得最终的残差矩阵E.

4 实例验证与分析

4.1 实验数据获取

选取北京市典型二环路作为实验交通路网,提取该交通路网(2011.06.09-2011.06.15)共7天的道路交通参数数据(统计流量、平均速度)进行实例验证.

选取道路交通参数数据的获取间隔Δt为 10 min,选取的路段一共有117条,故提取的原始道路交通参数矩阵X为大小为1 008×117的矩阵.

随机生成观测矩阵B,道路交通参数测量矩阵通过M=B.×X获得.

4.2 参数确定

提取7天的微波检测器的历史道路交通参数数据(2011.06.01-2011.06.07)来确定最优参数.在不同的道路交通参数数据缺失率下,随机生成不同的观测矩阵B.对不同的道路交通参数数据缺失率下,不同的参数r和λ对该算法的影响进行统计分析.

通过得到不同道路交通参数数据缺失率下的最优解所对应的(r,λ),可知:同一道路交通参数数据缺失率下,不同的道路交通参数(流量、速度)所对应的最优(r,λ)基本一致.r的取值随着道路交通参数数据缺失率的增大而减小；在取最优解所对应的r时,λ对算法的影响不大,最优解所对应的λ为0.1.根据统计的不同道路交通参数数据缺失率(prb)下最优解所对应的r,可知r的取值与交通状态数据缺失率有很强的线性关系,随着交通状态数据缺失率的增大而减小.r的取值有以下定义:

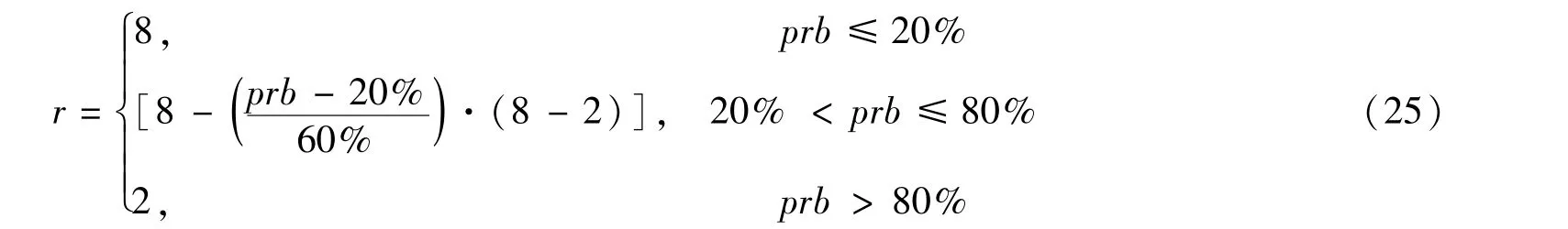
式中 prb为道路交通参数数据的缺失率.

4.3 残差矩阵确定

同样提取7天的微波检测器的历史道路交通参数数据(2011.06.01-2011.06.07)来确定残差矩阵.

4.4 实验结果

为使实验结果具有对比性,将实验结果与使用历史数据进行交通状态数据修复的结果进行对比.

利用归一化平均绝对误差及其对应的标准方差σ来检验测量精度,归一化平均绝对误差的标准方差σ定义如下:交通参数的归一化平均绝对误差,σsim是其对应的标准方差.

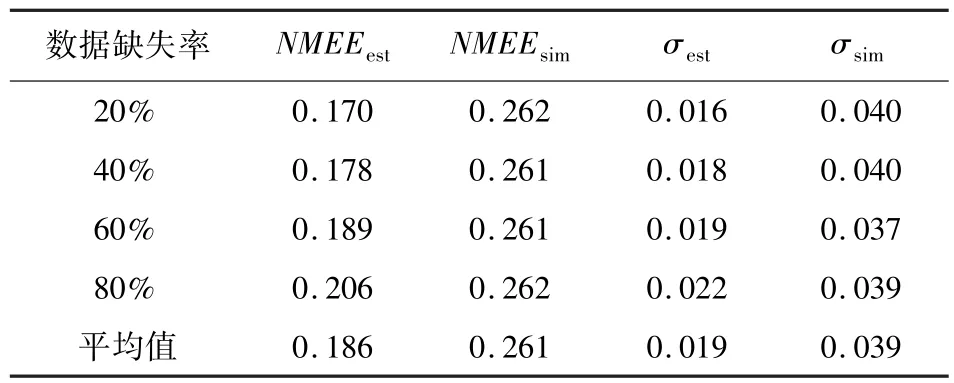
表1 道路交通参数(流量)获取对比结果Table 1 The comparison of the estimated results of road traffic parameters(traffic flow)

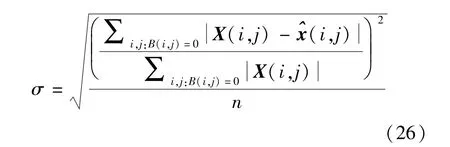
式中 n为实验编号.

获得的实验统计结果如表1和表2所示.其中,NMEEest是基于压缩感知获取的道路交通参数的归一化平均绝对误差,σest是其对应的标准方差；NMEEsim是基于历史交通状态数据修复的道路

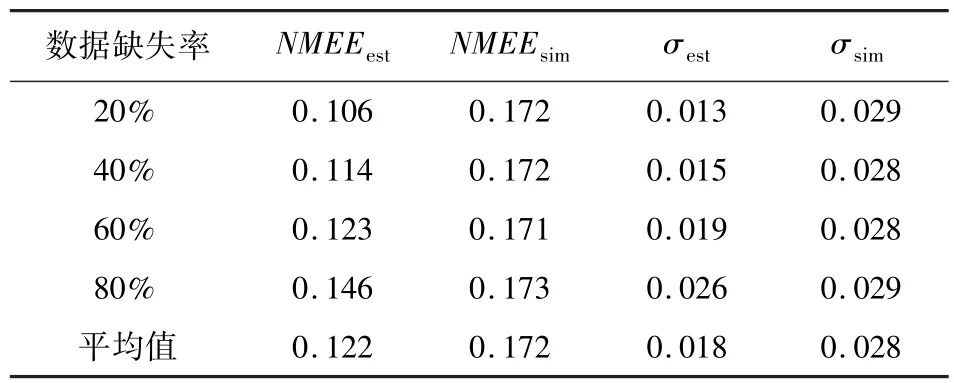
表2 道路交通参数(速度)获取对比结果Table 2 The comparison of the estimated results of road traffic parameters(statistical speed)

从表1和表2的统计结果,我们可以看出,基于压缩感知获取的交通状态数据(统计流量、平均速度)均优于基于历史交通状态数据修复得到的结果,具有较高的精度.即使在交通路网的交通状态数据缺失率高达80%时,基于压缩感知获取的道路交通参数的精度仍可达到80%左右.但交通路网的交通状态数据缺失率较小时,该算法获取的道路交通参数的精度还有待提高.故该算法较适用于交通路网的交通状态数据缺失率较高时.

误差的来源主要由两部分引起:

(1)微波检测器检测的速度存在误差.

(2)在基于压缩感知获取的道路交通参数的算法中,不同的交通状态数据集对应的最优参数和残差矩阵虽然相差不大,但毕竟各不相同.在参数设定的过程中,选取的最优的参数和残差矩阵均是历史交通状态数据的最优结果,与当前的最优参数和残差矩阵存在一定的差异.

5 研究结论

道路交通运行状态信息的获取是进行交通管理和控制的最重要的基础性工作.当交通路网的大面积交通状态数据缺失时,通过简单的历史数据补偿不能够实时有效地反映当前的交通运行状态.本文利用压缩感知的理论与方法,实现交通路网的交通运行状态数据的有效估计修复.基于压缩感知修复的道路交通运行状态数据具有较高的精度,其结果可以应用到区域交通状态分析、交通诱导及控制系统中.在交通路网的交通状态数据缺失率较高的情形下,该算法的适用性较好.在接下来的研究中,我们将对参数设定和残差矩阵的确定方法进行改进,以进一步提高算法的精度.

[1] MIN W,WYNTER L.Real-time road traffic prediction with spatio-temporal correlations[J].Transportation Research Part C:Emerging Technologies,2011,19 (4):606-616.

[2] 徐健锐,李星毅,施化吉.处理缺失数据的短时交通流预测模型[J].计算机应用,2010,30(4):1117-1120.[XU J R,LI X Y,SHI H J.Short-term traffic flow forecasting model under missing data[J].Journal of Computer Applications,2010,30(4):1117-1120.]

[3] XU Dong-wei,DONG Hong-hui,JIA Li-min,et al. Virtual speed sensors based algorithm for expressway traffic state estimation[J].Science China Technological Sciences,2012,55(5):1381-1390.

[4] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[5] Candes E J.The restricted isometry property and its implications for compressed sensing[J].Comptes Rendus Mathematique,2008,346(9):589-592.

[6] Lakhina A,Papagiannaki K,Crovella M,et al.Structural analysis of network traffic flows[J].ACM SIGMETRICS Performance Evaluation Review,2004,32(1):61-72.

[7] Candes E J,Recht B.Exact matrix completion via convex optimization[J].Foundations of Computational Mathematics,2009,9(6):717-772.

[8] Zhang Y,Roughan M,Willinger W,et al.Spatio-temporal compressive sensing and internet traffic matrices[J]. ACM SIGCOMM Computer Communication Review. ACM,2009,39(4):267-278.

The Recovery Algorithm for Road Traffic Parameters Based on Compressive Sensing

XU Dong-weia,b,DONG Hong-huia,b,LI Hai-jiana,b,JIA Li-mina,b
(a.State Key Laboratory of Rail Traffic Control and Safety；b.School of Traffic and Transportation, Beijing Jiaotong University,Beijing 100044,China)

To solve the road traffic parameters data problems(data invalid or data deletion)when a part of traffic states detectors in the road network break down,an algorithm based on compressive sensing is presented to repair traffic parameters of the road traffic network in this paper.Firstly,the road traffic parameters data are decomposed and approximated.Then the road traffic parameters recovery approach is presented based on compressive sensing,and the parameters setting referred in this road traffic parameters estimation approach based on compressive sensing is discussed.Finally,one typical road network in Beijing is adopted for the experiments analysis.The results show that this traffic states data recovery approach based on compressive sensing is feasible and can achieve a high accuracy.

intelligent transportation；traffic parameters recovery；compressive sensing；road traffic；data recovery

U491

A

U491

A

1009-6744(2013)06-0067-06

2013-06-25

2013-07-30录用日期:2013-08-16

国家“八六三”项目(2012AA112401,2011AA110505)；国家自然科学基金(61104164)；轨道交通控制与安全国家重点实验室自主课题(RCS2010ZT004).

徐东伟(1985-),男,山东威海人,博士生.

*通讯作者:jialm@vip.sina.com