不同气速下喷动床喷泉区颗粒特性的模拟分析
张彩虹,黄立新,谢普军,游 凤,张耀雷
(中国林业科学研究院林产化学工业研究所,生物质化学利用国家工程实验室,国家林业局林产化学工程重点开放性实验室,江苏省生物质能源与材料重点实验室,江苏 南京210042)
喷动床自20 世纪50年代问世以来,已被广泛应用于燃料燃烧、气化、物料颗粒干燥及催化聚合等工业过程中。由于在喷动过程中颗粒易于形成规律的循环流动,较随机而复杂的流化床有更多的优点,在工业过程中应用日益广泛。喷动床内气相与反应物的反应时间和停留时间依赖于床体几何结构和运行数,喷动床设计应满足不同应用要求。尽管喷射区、环形区和喷泉区内的气固两相流流体动力特性已有许多的实验研究,然而由于喷动床内气固两相流动的复杂性及测量条件的限制,人们对床体内运行参数对喷动床动力学的影响至今并不清楚。
为推广使用具有良好传热和传质效果的喷动床,国内外都做了大量的研究工作。刘伟民等[1]自行设计制造了喷动床粮食干燥机,以探索喷动床用于粮食干燥的实际效果和所存在问题的解决方法。He 等[2-3]设计了喷动床,对喷动床内固体颗粒在喷动区、喷泉区及环隙内空隙率及速率变化等进行了实验研究,为喷动床的流体力学研究提供了大量的实验数据。随着计算机技术的迅速发展,大量科研工作者热衷于喷动床的模拟研究[4-6]。Hosseini 等[7]采用欧拉-欧拉模型对喷动床内气固流速度矢量及气流速率进行模拟,考察了恢复系数及曳力系数的显著性,经过参数的优化研究,得出Wen-Yu 的曳力模型在无导喷管的模拟中为最佳模型。何玉荣等[8]采用颗粒弹性模量考虑颗粒与颗粒非弹性碰撞产生的颗粒作用力,考虑颗粒-颗粒滑动接触作用力,采用半理论-半经验颗粒相黏度模型,建立喷动床内气固两相双流体模型。模拟计算揭示同一气速下喷射区、环形区和喷泉区内颗粒体积分数、速度场等的分布,并与实验结果进行比较,在一定范围内有很好的吻合性,但是没有对不同气速对喷动床的影响进行分析。
尽管科研工作者对喷动床进行了大量研究,由于气固两项间的复杂变化,至今都没有对其相互影响完全知晓,模拟值与实验值间仍然存在较大差距。所以,无论是对喷动床模型的数值模拟还是实验研究数据都仍然相当缺乏。经过查阅相关文献发现,喷泉区作为喷动床最大气固表面接触区,对其模拟研究较少,一般是对同一气速下喷泉作简单的模拟,没有对这一区域变化进行详细分析研究。本文作者以自行设计的喷动床为模型,进行了气固两相模拟研究,即以喷泉区为研究对象,对其在不同气速下喷泉高度、喷动形态、颗粒体积分数、颗粒速度的变化及影响进行细微分析,获得模拟结果,为喷动床设计提供理论依据。
1 边界条件
本研究将欧拉多相流模型应用喷动床模拟,在下列条件基础上进行:①离散相与连续相共同存在,相互渗透,各相具有不同的速度、温度和体积分数;②认为离散相也有连续的速度、温度和体积分数分布;③两相流体间存在符合一定规律的能量、动量及质量传递。气固两相均满足质量守恒方程。根据Du 等[6]对不同曳力模型在喷动床模拟过程中的研究结果显示,Gidaspow 模型与实验结果有很好的一致性,所以选Gidaspow 模型来模拟气固相间的作用力。采用软件Fluent 6.3 进行模拟计算。
喷动床模型采用有限体积法对控制方程进行离散,Simple 算法对速度与压力进行耦合求解,模拟采用两维轴对称。网格采用结构式划分方法,并对其进行网格独立性验证,网格增加对模拟结果影响不大。空气为基本相,给定入口边界为速度入口,入口处湍流定义方法使用湍流强度与水力直径,湍流强度5%。气体不可压缩。以颗粒(绿豆)作为第二相,进口速度为零。出口采用压力出口,压力梯度取为零。对气相,壁面采用无滑移边界条件。壁面处颗粒相采用自由滑移边界条件。假设颗粒间碰撞为弹性碰撞,认为碰撞后恢复系数为0.9 时就达到弹性碰撞,最大体积分数采用Du 等[5]的研究结果,即0.59。
对于最小喷动气速可由Mathur(1994)的经验公式获得,见式(1)。
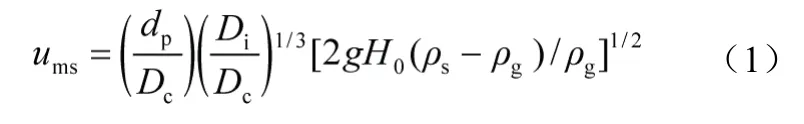
根据式(1)计算得出ums为0.317 m/s,但在此气速下喷动床无法形成喷动形态。当气速增加到0.42 m/s 时,虽然没有形成喷动态,但颗粒表面颗粒开始松动,床层略有升高,轴线处有微凸状。故将此气速定位本模拟实验的最小喷动气速,其与计算得出的最小喷动气速(0.32 m/s)约1.3 倍的关系。模拟基本数据如表1 所示。
2 结果与分析讨论
2.1 网格独立性验证
由于网格的划分方法对喷动床的模拟结果有重要的影响,故需对网格的划分方法进行研究。为了验证网格划分方法的可行性,以经典模型He 模型进行验证[2]。He 模型模拟数据见表2。
采用网格轴向间距为2.5 mm,共550 格;径向是38 格,从轴中心以等比例1.01 沿径向增加的方法,其模拟结果如图1 所示,在0.268 m 床层高度轴心处模拟值与实验值误差最大,为18.2%,其它误差均小于此值。可见,此网格划分方法在一定范围内具有一定的可行性[9]。故本文采用此结构化方法对本喷动床进行研究。由于网格的多少会影响模拟结果,需要进行网格独立性研究,轴向网格间距分别为5 mm、4 mm、2 mm;径向分别是44 格、55 格、110 格,从轴中心以等比例1.01 沿径向增加,网格总数如表3 所示。3 种网格下模拟空隙率结果如图2 中所示。由图2 可以看出,随着网格数的增加,在喷动区空隙率趋于均匀,不考虑在环隙区颗粒的变化,55000 格与13750 格空隙率的相对差值在5%内。可见变化值较小,为减小计算工作量,选择13750 格为本模拟实验网格数。

表1 模拟数据

表2 He 模型模拟数据
2.2 不同气速喷动现象模拟

图1 He 模型喷动区空隙率(h=0.218m)
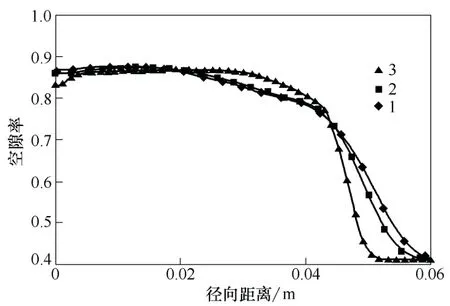
图2 喷动区空隙率(h=0.2m)

表3 网格数量
考察了固体颗粒在不同气速下的喷动情况,采用粒径为0.003 m 的颗粒,在不同气速下模拟喷动。由于喷泉区为主相与第二相的主要接触区,无论是传质还是传热过程大部分都会在这个区域内完成,喷泉区内各种状态的变化都会对结果产生影响,故本文作者主要对喷泉区内颗粒的变化特性进行了研究。图3 为喷动气速在(1.0~1.8)ums下颗粒的喷动形态。从图3 中可以看出,喷动床中心为低颗粒体积分数的喷射区,在喷射区和床壁面间形成高颗粒体积分数的环形区,在喷动床顶部形成相对较低颗粒体积分数的喷泉区。在气速为1.0ums时,0.003 m的颗粒均不能起喷,这是由于气速不能克服床层物料所形成得压力降;随着进口气速的增加,喷泉高度逐渐升高。这与Wu 等[10]观点一致,气体速率越大产生的喷泉高度就会越高。图4 为u/ums气速在1.0~1.8 条件下喷泉高度曲线,认为当颗粒体积分数小于5×10-7时为喷泉最高点。由图4 可知,除去1.0~1.2 段,喷泉高度与气速成很好的线性关系,线性方程为Hf=0.4279(u/ums)-0.23,R2=0.9997。对u/ums=1.25 时进行模拟对方程进行了验证,模拟稳定后Hf=0.304。由方程计算所得Hf=0.3049,误差小于1%,可见方程与模拟结果具有很好的吻合性,在u/ums为1.2~1.8 范围内,气速与喷泉高度成很好的线性关系,但确切结果还有待于实验验证。
2.3 喷泉区颗粒体积分数的变化
由于是对喷泉区颗粒体积分数的分析,故所指床层高度均为除去静止床层0.3 m 以上的喷泉区高度(ZF)。图5 为喷动气速为1.1ums时不同高度颗粒体积分数变化。由图5 可以看出,固体颗粒体积分数在轴心区域较高,随着径向距离的增加颗粒体积分数逐渐下降;这是由于在曳力作用下,高体积分数颗粒与高速气流一起由喷动区进入喷泉区,沿轴心区域向上运动,在喷泉区内空间区域变大,气体在径向的扩散作用变大,曳力逐渐变小,颗粒由加速逐渐变为减速运动,当速度为零时,到达最高位置,颗粒在重力作用下开始向下回落,同时又受到径向扩散气流的曳力,在径向缓慢运动。形成围绕轴心区的环形回落区,由于沿径向空间区域逐渐变大,空隙率变大,所以出现体积分数下降的趋势。由图5 中还可以看出,在轴心区域,颗粒体积分数随高度的增加呈现先减小后增大的趋势,而且喷泉宽度随着高度的增加逐渐减小。这是由于颗粒在低床层位置时,高浓颗粒被高速气流由喷动区带入喷泉区,随着高度增加,受曳力作用较小的外围颗粒不断回落,所以颗粒体积分数逐渐下降;当接近最高点时,上升及下降颗粒都急剧在轴心范围,所以颗粒体积分数逐渐增大。当喷动气速为1.2~1.8ums时,颗粒体积分数变化与此相同。这种变化趋势与He 等[3]的实验结果一致。

图3 不同气速下颗粒的喷动形态(u/ums)
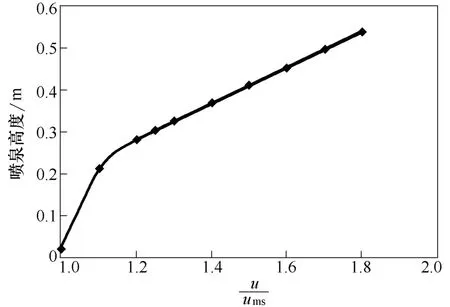
图4 在不同气速下喷泉高度曲线

图5 喷泉区颗粒体积分数分布(u/ums=1.1)
图6 为喷泉区床高为0.025 m 时,不同气速下颗粒体积分数的变化。由图6 可以看出,颗粒体积分数随着喷动气速的增加而减小,但是减小幅度不同。喷动气速由1.1ums增大到1.2ums时,轴线处颗粒体积分数约减少0.057;由1.2ums增大到1.3ums时,轴线处颗粒体积分数约减少0.033;由1.3ums增大到1.5ums时,颗粒体积分数基本不变。由1.5ums增大到1.6ums时,轴线处颗粒体积分数约减少0.029;由1.5ums增大到1.6ums时,轴线处颗粒体积分数又变化很小。在随喷动气速增加时,总体趋势是随着喷动气速的增大轴心区颗粒体积分数明显减小,减小幅度逐渐下降,这与Szafran 等[11]的研究结果相吻合。但是出现两段区间,颗粒体积分数随(ZF=0.025 m)喷动气速变化不明显。由于没有发现相关文献,具体结果还需要实验验证及探究起因。由图6 中还可以看出,随着喷动气速的增加,在喷泉区0.025 m 床层高度处,颗粒在径向的分布宽度逐渐增加。这是由于喷动速度较大时,喷泉高度增加,颗粒回落时相对低喷泉高度运行时间就会增大,扩散气体作用的径向运行时间也会增加,所以会逐渐变宽。这也解释了图5 中所示的,在喷泉外围区随喷泉区床层高度增加喷泉宽度逐渐减小的原因。

图6 不同气速相同床层高度颗粒体积分数(ZF=0.025 m)
2.4 喷泉区速度的变化
图7 为喷动气速为1.1ums时,喷泉区不同床层高度颗粒速度径向分布。图7 中显示颗粒速度随床层高度的增加逐渐减小,这是由于颗粒受到重力作用的结果。喷泉核心区和喷泉外围区运动方向不同,在喷泉核心区颗粒向上运动,速度为正值;而在喷泉外围区颗粒向下流动,速度为负值。沿半径方向可以看到,在喷泉区轴心处为最大值,且沿径向逐渐减小,颗粒速度出现零时为颗粒上升区与下降区的分界点。在喷泉外围区颗粒向下流动,由分界点开始,在重力作用下做加速运动,速度逐渐增加,且随床层高度增加而减小。这些变化趋势与He 喷动床实验喷泉区径向速度分布结果基本相符。当喷动气速为1.2~1.8ums时,颗粒速度变化与此相同。
由图8中相同床层高度颗粒速度变化(ZF=0.025 m)可知,同一床层高度上的颗粒随气速的增加速度增大。这是显而易见的,由于随着喷动气速增加,气固间曳力也会逐渐增大。但随着喷动气速的增加,颗粒速率上升的幅度是不同,而且基本无规律可循。由图中可见,在轴心处,喷动气速由1.1ums增大到1.8ums过程中,颗粒速度在两端变化幅度较大,中间变化较小,最大幅度发生在1.1~1.2ums间,约为0.39;最小幅度在1.6ums增大到1.7ums时,速度变化甚微。这可能与模拟过程中的升力、虚体质量力等其它作用力有关。

图7 喷泉区颗粒速率径向分布(u/ums=1.1)
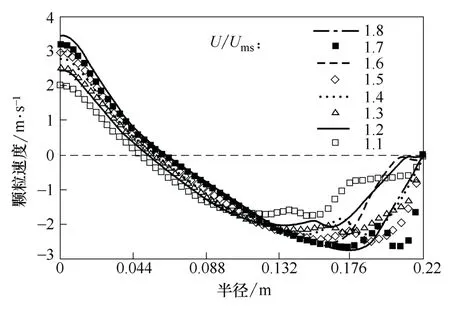
图8 喷泉区相同高度不同速率下径向分布(ZF=0.025 m)
3 结 论
(1)喷泉高度随气速的增加而增大,且在u/ums=1.2~1.8 范围为线性关系,线性方程为Hf=0.4279(u/ums)-0.23,R2=0.9997。
(2)固体颗粒体积分数在轴心区域较高,随着径向距离的增加逐渐下降,且随高度的增加呈现先减小后增大的趋势,而且喷泉宽度随着高度的增加逐渐减小;颗粒体积分数受速率的影响较大,随着喷动速率的增大颗粒体积分数趋于减小,但减小幅度不同。
(3)在喷泉核心区颗粒速度随床层高度增大而减小。喷泉核心区和喷泉外围区运动方向不同,在喷泉核心区颗粒向上运动,速度为正值;而在喷泉外围区颗粒向下流动,速度为负值。同一床层高度上的颗粒速度随气速的增加而增大,但增大值不同。
符 号 说 明
Dc—— 床体直径,m
Di—— 入口直径,m
dp—— 颗粒直径,m
e—— 恢复系数
H—— 床体高,m
H0—— 静止床层高,m
ums—— 最小流化速度,m/s
ρg—— 气相密度,kg/m3
ρs——固相密度,kg/m
θ——底角锥度,(°)
ωs.max—— 最大体积分数
[1] 刘伟民,陈健,徐圣言,等. 导向管喷动床小麦干燥工艺优化研究[J]. 农业工程学报,2003,19(6):197-200.
[2] He Y L,Qin S Z,Lim C J,et al.Particle velocity profile and solid flow patterns in spouted beds [J]. The Canadian Journal of Chemical Engineering,1994,72(8):561-568.
[3] He Y L,Lim C J,Grace J R,et al.Measurements of voidage profiles in spouted beds[J].The Canadian Journal of Chemical Engineering,1994,72(4):229-234.
[4] Wu Z,Arun S A.CFD modeling of the gas-particle flow behavior in spouted beds[J].Powder Technology,2008,183:260-272.
[5] Du W,Bao X,Xu J,et al.Computational fluid dynamics (CFD)modeling of spouted bed:Influence of frictional stress,maximum packing limit and coefficient of restitution of particles [J]. Chemical Engineering Science,2006,61:4558-4570.
[6] Du W,Bao X,Xu J,et al. Computational fluid dynamics (CFD)modeling of spouted bed:Assessment of drag coefficient correlations[J].Chemical Engineering Science,2006,61:1401-1420.
[7] Hosseini S H,Zivdar M,Rahimi R.CFD simulation of gas-solid flow in a spouted bed with a non-porous draft tube [J]. Chemical Engineering and Processing,2009,48:1539-1548.
[8] 何玉荣,陆慧林,刘文铁,等. 喷动床内气固两相流体动力行为的数值模拟[J]. 化工学报,2004,55(2):290-296.
[9] 黄明辉. 喷动床内气固两相流体流动数值模拟[D]. 西安:西北大学,2009.
[10] Wu S W M,Lim C J,Epstein N.Hydrodynamics of spouted beds at elevated temperatures[J].Chem.Eng.Comm.,1987,62:251-268.
[11] Szafran R G,Kmiec A. Periodic flucuations of flow and porosity in spouted beds[J].Trans.Porous.Med.,2007,66:187-200.

