我国财产保险公司承保业务线经济资本的度量
陈迪红,王清涛
(湖南大学 金融与统计学院,湖南 长沙 410079)*
一、引 言
目前,随着金融服务业竞争的加剧,金融保险集团对其资本管理的要求越来越高。对于保险公司而言,既要满足法律法规设定的最低偿付能力,又要满足股东对利润的诉求。资本管理的新趋势是经济资本。经济资本最初于2004年由巴塞尔委员会提出,但至今仍然没有一个统一的定义。本文使用巴塞尔委员会的定义,即:经济资本是指在一定时间长度下、一定置信度下,能够缓冲企业的非预期损失所需要的资本。经济资本方法可以在同一框架下考虑保险公司所有的风险,而且能够很好地满足保险公司同时对偿付能力与盈利能力的追求,故而在国际范围内逐渐被保险业认可。如何合理地计量经济资本是使用经济资本框架的关键。
经济资本的度量主要有两个方面的问题:一是损失分布的获取,二是风险的度量方法。保险公司的业务结构一般都比较复杂,若想获得损失分布,就要先考虑业务结构的相关性。Copula方法的出现在一定程度上解决了相关性的问题。Bagarry Marc(2007)使用了Gauss Copula和多元 T-Copula度量了财产保险公司的经济资本[1]。Andrew Tang et al(2009)检验了不同椭圆族Copula相依结构下的资本要求和资本分散效应[2]。国内的占梦雅(2010)考虑了椭圆族Copula相依结构下经济资本的测算[3]。这几篇文献仅仅考虑了椭圆族Copula,但是,高维椭圆族有很大的局限性。
风险度量方面,国内外文献中提及的方法主要是 VaR、TVaR 和 TCE 等风险 度量方 法[1-3]。但VaR不能体现超过分位点的损失,而且其只对椭圆族分布才满足次可加性。TVaR与TCE这两种风险度量方法对采取使结果小于分位点的行动没有激励,而且也没有对极低频率、极大损失进行调整。Dhaene,J et al(2004)总结了前人的工作,指出凹扭曲风险度量可以在一定程度上解决上述问题[4]。凹扭曲风险度量的核心是其对应的凹扭曲函数,通过灵活地构造凹扭曲函数,可以获得不同的凹扭曲风险度量方法。比较著名的一些凹扭曲风险度量方法有PH扭曲风险度量方法、Wang变换、Lookback扭曲风险度量方法等[5-7]。整合文献,发现国内学者暂时没有采用凹扭曲风险度量来测度经济资本。
承保风险是保险公司面临的主要风险之一。如何合理地度量业务线之间的相关结构对于保险公司十分关键。本文将通过运用高维Copula理论获得我国财险公司的赔付率分布,并比较高维椭圆族与高维阿基米德族Copula相关结构对结果的影响,然后,在一定置信度下通过凹扭曲风险度量获得风险调整后的赔付率,最后,结合公司的保费收入估计出财险公司承保业务线应持有的经济资本。
二、Copula理论与经济资本度量模型
(一)Copula理论
Sklar在1959年发表的Sklar定理在Copula理论研究中具有重要的地位。利用Sklar定理,风险管理者可以自由地把任意N个一元边际分布构成一个N元的联合概率分布函数。Copula函数刻画的是随机变量之间的相依结构。选择的Copula不同,联合分布就不同。具体的Copula的种类及其相关性质可以参考 Cherubini(2004)[8]。
(二)经济资本度量模型
经济资本度量模型主要包括两个方面的内容:其一是损失分布的获取,其二是风险的度量(非预期损失的度量)。
1.损失分布的获取。由于保险公司的赔付率分布往往比赔款分布更加稳定,这里先求出一定置信度下的赔付率,然后再乘以当年的保费收入,即可得出保险公司应持有的经济资本。
赔付率分布获取的具体步骤如下:
(1)参数估计。此步骤包括各业务线赔付率边缘分布的参数估计和待选族Copula的参数估计。边缘分布的参数估计使用极大似然估计方法。对于待选族Copula的参数估计,IFM方法和CML方法比精确极大似然估计方法要高效[8],而且参数分布比经验分布更加灵活,故本文采用IFM方法。
(2)Copula的选取方法。一般的拟合优度检验,如 Kolmogorov-Smirnov检验和 Anderson-Darling检验,对于普遍意义上的多维分布比较困难。本文采取Aas(2004)的方法,选取与经验Copula全空间下欧氏距离最小的Copula[9]。
(3)随机模拟及最终赔付率分布的获取。依据步骤(2)选出的Copula,模拟一定数量的样本,再对各业务线的模拟样本进行加权,权重为各业务线保费收入与总保费收入的比值(证明如下),然后可以得到最终的分布。

2.非预期损失的度量。本文采取凹扭曲风险度量方法度量非预期损失。扭曲风险度量[10]的具体定义如下:设Y是一表示损失的非负随机变量,g(·)是定义在区间[0,1]上,并且g(0)=0,g(1)=1的单调非减函数,ρg[Y]=g(S(y))dy被称为Y的扭曲风险度量,其中g(·)为扭曲函数。当g(·)为凹函数时,ρg[Y]为凹扭曲风险度量。比较著名的凹扭曲风险函数如下:
(1)TVaR扭曲函数:
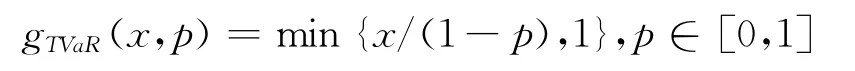
(2)Proportional Hazard(PH)扭曲函数:

(3)Lookback(LB)扭曲函数:

(4)Wang扭曲函数:


其中:

由扭曲函数g(·)非减且g(0)=0,g(1)=1可知:p*i≥0,i=1,…,n且=1。
扭曲风险度量方法下,非预期损失(经济资本)为:
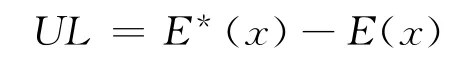
三、算例分析
(一)数据的来源及边缘分布的拟合
经济资本度量的周期一般都为1年。本文假设月度赔付率与年度赔付率的分布相同,这样就可以通过收集月度数据以解决样本数量不足的问题。
以某财险公司2007年1月~2012年6月全国范围的业务线月度数据为基础,测度该公司机动车辆保险、企业财产保险、责任保险三种险种所需要的总经济资本。剔除异常数值之后,共64个样本。其中三条业务线的赔付率基本统计特征见表1。
根据以上各险种赔付率分布的特点进行拟合优度检验,最后决定使用以下分布拟合各险种赔付率(见表2)。

表1 各业务线赔付率的基本统计特征

表2 各险种边缘分布的拟合结果
GEV分布为广义极值分布,Lognormal为对数正态分布。GEV分布的分布函数为:

(二)Copula函数参数的估计及选取
由于尾部相关性的大小在很大程度上影响着最终的损失,故只考虑能够较好反映上尾相关性的标准Gumbel阿基米德Copula和椭圆族Copula,并从中选取拟合效果最好的Copula来度量业务线之间的相关结构。
采用边际推断函数法(IFM方法)来估计各Copula的参数,结果见表3、表4。

表3 Gauss Copula的相关矩阵

表4 多元T-Copula相关矩阵及自由度
标准Gumbel Copula参数估计:

依据Aas(2004)文中Copula选取的方法,各Copula与经验Copula的距离见表5。
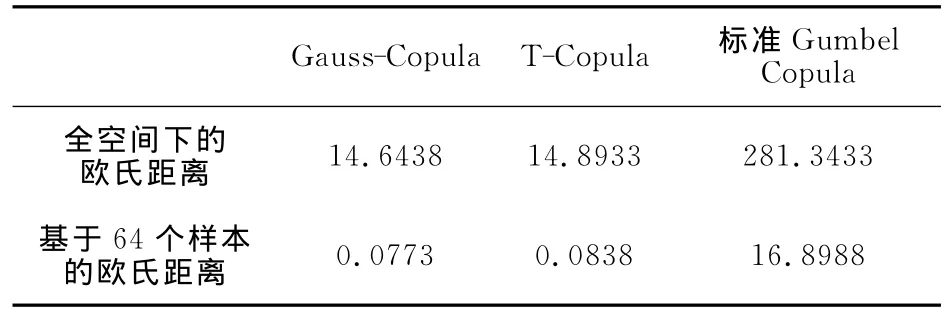
表5 各Copula与经验Copula的距离
距离最小的是 Gauss Copula函数,故采用Copula来模拟三条业务线之间的相关性。但是从表5中距离可以看出,T-Copula与Gauss Copula的差距很小,标准Gumbel Copula与这两个的距离差距较大,故下面将以T-Copula的相依结构作对比分析。
(三)Copula的随机模拟及赔付率分布的获得
这三种险种的各自保费收入与总保费收入的比例各自的赔款与该公司总赔款的比例如表6。

表6 保费收入与赔款支出的占比 (%)
对各业务线的赔付率进行加权平均,可以得到最终的赔付率,其中,权重为各业务线保费收入与总保费收入的比。
对于三条业务线而言,权重为各业务线标准化之后的比例,其值见表7。

表7 各业务线的权重 (%)
Gauss Copula模型下,使用 Cherubini(2004)P181中的方法模拟1万次。然后将模拟的数据进行加权,权重为各业务线的保费收入与总保费收入占比标准化之后的数值。在此给出T-Copula模拟结果做对比,赔付率的直方图分别见图1和图2。

图1 Gauss Copula下模拟的赔付率直方图

图2 T-Copula下模拟的赔付率直方图
(四)经济资本的计量
本文采用凹扭曲风险度量方法决定经济资本。当采用PH风险度量和LB风险度量决定资本时,风险的置信水平与其参数没有必然、直接的关系,所以,本文只给出TVaR与Wang变换风险度量下的经济资本。关于置信度,取一些具有代表性的置信度,并在各置信度下,计算赔付率的数值,得出非预期赔付率。再用非预期赔付率的数值,乘以该公司当年的保费收入,即可估算出为这三条业务线应持有的经济资本。
由于保费收入的变化比较大,而赔付率往往相对比较稳定,故在此只给出赔付率的具体数值。本文最终选取的Copula为Gauss Copula,在此相依结构下VaR与各凹扭曲风险度量的结果如表8所示。同时给出T-Copula相依结构下VaR与各凹扭曲风险度量的结果作对比,结果如表9所示。

表8 Gauss Copula下的VaR与凹扭曲风险度量的结果

表9 T-Copula下的VaR与凹扭曲风险度量的结果
(五)解释
从表8可以看出,Wang风险度量决定的经济资本在VaR方法与TVaR方法之间。Wang风险测度能够根据风险的水平,灵活地调整所需的经济资本。Wang风险度量可以对尾部的极低频率、极大损失进行调整。从图1可以看到,模拟分布的右端有一部分极低频率、相对极大的损失数值。对于保险公司来说,Wang风险度量在某种程度考虑了巨灾风险,并考虑了投保人的自我防损,相比VaR、TVaR而言更加合理。
在经济资本的测算中,可以注意到,表9中低置信度下的TVaRα数值要比表8的小,高置信度下的数值要比表8的大,由此,T-Copula比Gauss Copula厚尾的性质也得到了验证。
四、结 论
以上使用多元Copula相依结构模拟业务线之间的相依结构,并采用了凹扭曲风险度量方法测度了我国某公司承保业务线的经济资本。结论如下:
(1)多元正态Copula适合模拟该公司业务线的相关结构。
(2)凹扭曲风险度量中的 Wang风险度量能够灵活地依据风险的水平对所需的资本进行调整,Wang风险度量的数值始终介于VaR与TVaR之间,当风险逐渐变大时,Wang风险度量与VaR之间的距离在增大,与TVaR的距离呈现缩小的趋势。
Wang风险度量可以对尾部极低频率、极大损失进行调整,可以根据风险整体水平灵活地调整公司所需持有的经济资本。此方法下的经济资本可理解为经过风险调整后的平均损失与未经风险调整的平均损失的差额,比VaR与TVaR方法下的数值更加合理。下一步,我们将研究如何度量更多条业务线的经济资本。
[1]Bagary Marc.Economic capital:aplea for student copula[J].Meeting paper for the 28th International Congress of Actuaries.2007.
[2]Andrew Tang and Emiliano A.Valdez.Economic capital and the aggregation of risks using copulas[J].Meeting paper for the 28th International Congress of Actuaries.2009.
[3]占梦雅,吴述金.多元Copula相依结构下财险承保业务经济资本计量 [J].华东师范大学学报(哲学社会科学版),2010,(2):89-94.
[4]Dhaene,J.Vanduffel S.Goovaerts,M,J.et al.Risk measuves and comonotonicity:a review[J].Stochastic Models,2006,22(4):573-606.
[5]Shaun Wang.Premium calculation by transforming the layer premium density[J].Astin Bulletin,1996,(26):71-92.
[6]Shaun Wang.A class of distortion operators for pricing financial and insurance risks[J].The Journal of Risk and Insurance,2000,67(1):15-36.
[7]W.Hürlimann.Inequalities for lookback option strategies and exchange risk modelling[R].In Proceedings of the 1st Euro-Japanese Workshop on Stochastic Modelling for Finance,Insurance,Production and Reliability,Brussels,1998.
[8]Cherubini,U.Copula methods in finance[M].Wiley,2004:129-194.
[9]Aas,K.Modeling the dependence structure of financial assets:a survey of four copulas[J].Research Report SAMBA .2004/22/04,Norwegian Computing Center.
[10]Bellini,F.,Caperdoni,C.Coherent and Distortion Risk Measures and Higher-order Stochastic Dominances[J].North American Actuarial Journal,2007,11(2):35-42.
[11]陈迪红,桂芬.基于拓扑数据模型的车险操作风险度量[J].财经理论与实践,2012,(4):17-21.

