粗粒度并行遗传算法的MapReduce并行化实现

程兴国，肖南峰

(华南理工大学计算机科学与工程学院，广州 510006)

遗传算法(genetic algorithm，GA)是一类借鉴生物界自然选择和遗传机制的启发式随机搜索算法，它是将生物学中的遗传进化原理和优化理论相结合的产物。遗传算法的基本思想很简单，它通过模拟生物界“物竞天择，适者生存，优胜劣汰”的策略获取种群全局最优解。

遗传算法作为一种应用广泛的高效智能搜索算法，己经成功地应用于工程设计、工商管理、科学实验等领域中的复杂优化问题的求解。随着信息技术的进步以及信息化社会的发展，遗传算法的种群规模和迭代代数显著增加，导致串行计算方法的时间复杂度比较高，处理能力存在局限性。传统高性能计算中的并行编程模型(如PThread、MPI和OpenMP等)抽象度不高，开发人员需要熟悉底层的配置和并行实现细节［1］。MapReduce模型是Google实验室提出的分布式并行编程模型或框架，它能在普通的PC机上构建集群来处理大规模数据集，成为云计算平台主流的并行数据处理模型。Apache开源社区的Hadoop项目用Java语言实现了该模型，同时Hadoop项目还设计了开放源代码的云计算技术平台［2］。本文在基于Hadoop技术的云计算基础平台上研究了粗粒度并行遗传算法的MapReduce并行编程实现方法，并进行了相关实验。

1 MapReduce编程模型

MapReduce编程模型的基本思路是将大数据集分解为成百上千的小数据集splits，每个(或若干个)数据集分别由集群中的1个节点(一般是1台普通计算机)并行执行Map计算任务(指定了映射规则)，并生成中间结果，然后这些中间结果又由大量的节点并行执行Reduce计算任务(指定了归约规则)，形成最终结果。图1描述了MapReduce的运行机制:在数据输入阶段，JobTracker获得待计算数据片在NameNode上的存储元信息;在Map阶段，JobTracker指派多个TaskTracker完成Map运算任务并生成中间结果;在Partition阶段完成中间结果对Reducer的分派;在Shuffle阶段完成中间计算结果的混排交换;JobTracker指派TaskTracker完成Reduce任务;Reduce任务完成后通知JobTracker与NameNode以产生最后的输出结果。MapReduce详细执行过程如图1所示［3］。

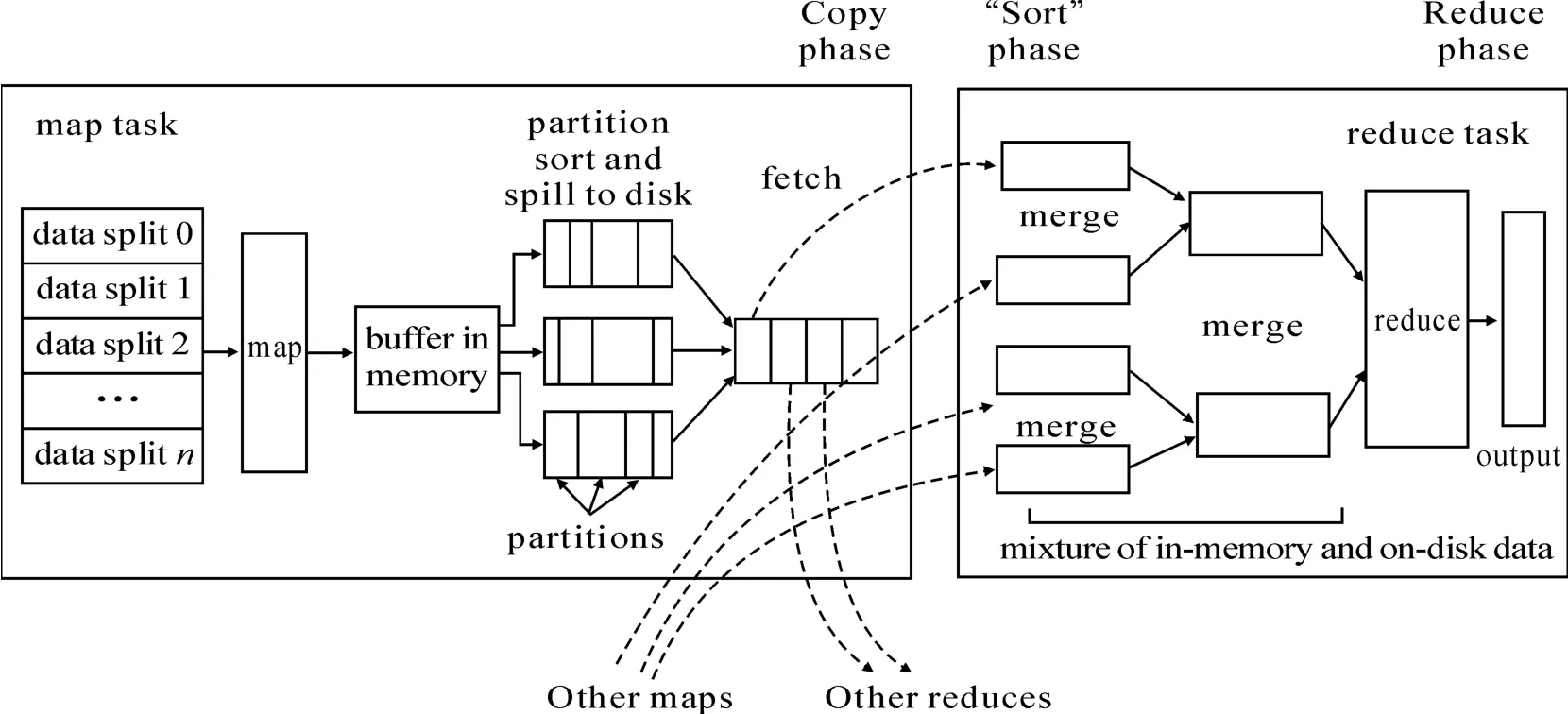
图1 MapReduce详细执行过程

2 粗粒度并行遗传算法

遗传算法(GA)是自然遗传学和计算机科学相互结合渗透而成的算法，是具有“生成+检测”的迭代过程的搜索算法，即产生、选择优良个体、基因组合(变异)、再产生、再选择、再组合…［4］，其基本流程如图2所示。

图2 遗传算法流程

传统的遗传算法有两个严重的不足:①容易过早收敛;②在进化后期搜索效率较低，使得最终搜索得到的结果往往不是全局最优解而是局部最优解，并且该算法不能有效克服过早收敛现象［5］。因此，现有的大量研究集中于如何改进传统的遗传进化思想。目前各种改进思想层出不穷，粗粒度模型就是其中的一种。

粗粒度模型又称分布式模型(distributed style)或孤岛模型(island-based model)，是适应性最强和应用最广的遗传算法并行化模型［6］。它将随机生成的初始种群依处理器个数分割成若干个较大的子种群，各个子种群在不同的处理器上相互独立地并发执行遗传操作，每经过一定的进化代数，各子种群间再相互交换若干数量的个体，以实现各个子种群的共同进化。

对经典遗传算法进行粗粒度并行改进的主要目的是:在不增加适应度计算量的基础上，通过提高种群多样性来提高计算结果。

粗粒度并行遗传算法(CPGA)可以形式化地定义为一个三元组:

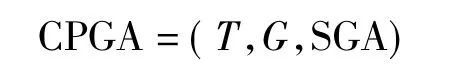
式中:T是进行迁移操作的时间间隔(频率);G是迁移操作所交换的个体和信息;SGA是经典遗传算法(单一种群)，它将根据子种群的数量多次重复地执行。

粗粒度并行遗传算法的子种群间常用的环行连接结构［7］如图3所示。

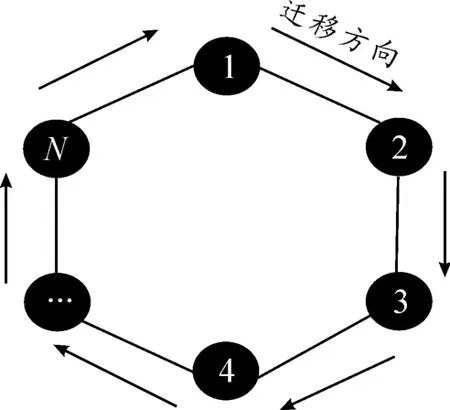
图3 子种群环形连接结构

3 粗粒度并行遗传算法的MapReduce并行化实现

粗粒度并行遗传算法进行MapReduce的基本思路是:把串行遗传算法的每一次迭代变为一次MapReduce操作。其中，在Map中完成计算个体适应值、杂交、变异的操作;Reduce则判断是否满足收敛条件，若为“是”则输出结果，否则进入下一次MapReduce操作。与普通的MapReduce操作不同，在Map阶段结束后，粗粒度并行遗传算法MapReduce通过Partition实现并行化，在子种群间用环行算法迁移最优个体，而其他大部分个体保持独立，如图4所示。

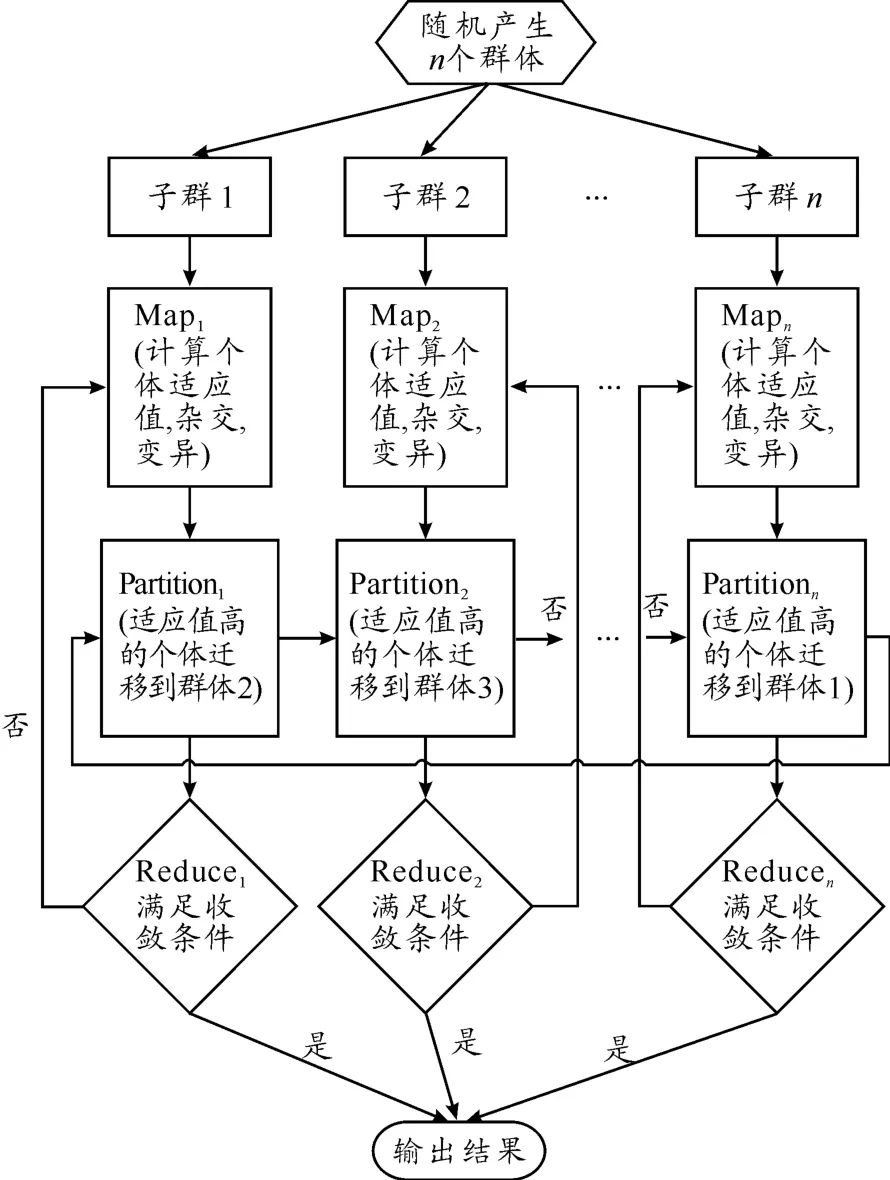
图4 粗粒度并行遗传算法MapReduce的并行化实现

为了保证各个子群独自繁衍，Mapper和Reducer的节点数量都为n，同时确保 Mapperi的数据在对应的Reduceri进行处理。待处理的每个个体给予一个子群key，在Map处理过程中，最优个体的key=(key+1)mod n，而Partition的操作是key mod n，从而实现最优个体的环形迁移。

3.1 Map函数的设计

Map函数先对子群中的个体进行杂交、变异操作，然后遍历子群，计算其适应值，根据适应值找出子群中的最优个体和最差个体，最优个体用于迁移到下一个子群(key+1)mod n，而淘汰最差个体。当然，也可以实现迁移若干最优个体，但数量不宜过大，否则会影响子群的差异性。

Map函数伪代码清单

3.2 Partition函数的设计

Partitioner的主要任务是对中间结果key-value对进行划分，以决定将其分配至哪个 reducer［8］。

Partition函数的伪代码清单如下:

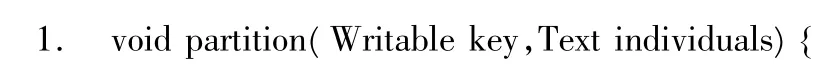
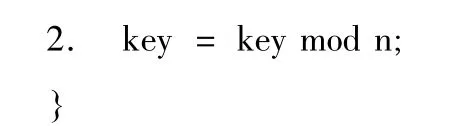
3.3 Reduce函数的设计

Reduce函数主要是判断遗传算法的终止条件，如果满足条件则终止，输出最终结果，否则进入下一轮的MapReduce循环。

Reduce函数的伪代码清单如下:

4 实验和结果分析

4.1 环境搭建

实验中云计算平台的结构:1台机器作为NameNode和JobTracker的服务节点，其他8台机器作为DateNode和TaskTracker的服务节点。每台节点的硬件配置如下:CPU型号为Intel(R)Core(TM)Duo T8300@2.40GHz;内存为 2GB;硬盘为2TB;基于 hadoop－0.20.2 版本构建集群。

4.2 单机处理比较实验

本文采用的算例是Shubert函数。它是一个典型的多峰问题，有760个局部最小，其中18个是全局最小，Shubert函数的仿真如图5所示，函数如下:

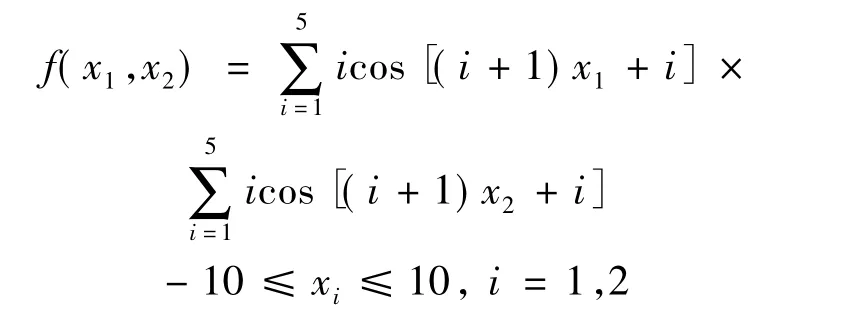
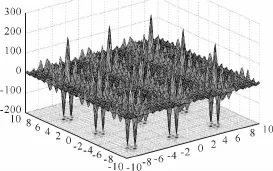
图5 Shubert函数的仿真

遗传算法的实验参数设置:

NIND=120;%个体数(number of individuals)

MAXGEN=50;%最大遗传代数(maximum number of generations)

NVAR=2;%变量数目

PRECI=25;%变量二进制位数(precision of varibles)

GGAP=0.9;%代沟(generation gap)

实验结果如表1所示。

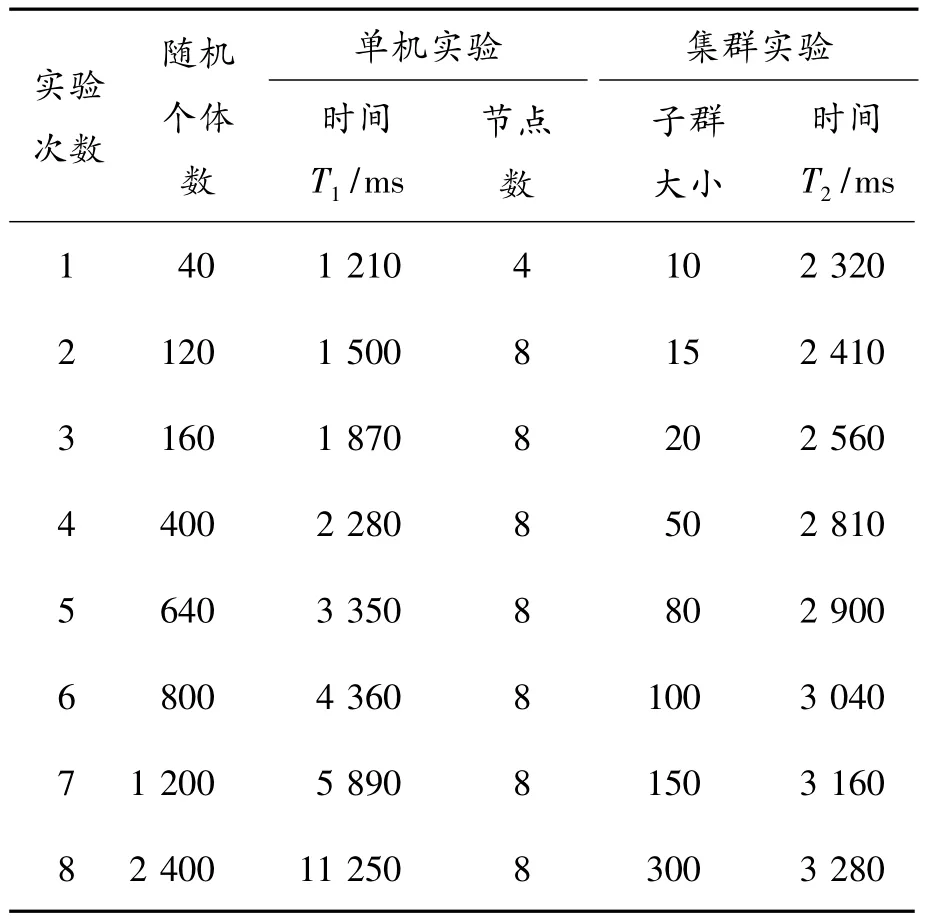
表1 Shubert函数实验结果比较

从表1不难得出，当随机个体数在640以下时，单机的性能比集群的要好。这是因为集群有节点间的通信开销，此时通信时间占主要地位。随着个体数的增加，集群的优势逐渐表现出来，尤其是海量数据的处理，其优势更加明显。

图6 Shubert函数实验结果对比

4.3 集群加速比实验

加速比是衡量一个系统在扩展性方面优劣的主要指标，主要考察计算硬件资源增加时，对于相同规模的作业，系统的处理能力。

实验分别选择1、3、6、8 个 TaskTracker节点参与随机个体数为1 200的计算，考察在逐渐增加节点的情况下系统完成任务的时间。实验结果如图7所示。从图7可以看出:每个作业运行的时间都随着节点的增加而降低，增加节点可以显著地提高系统对同规模数据的处理能力，这说明MapReduce在处理遗传算法方面具有较好的加速比。

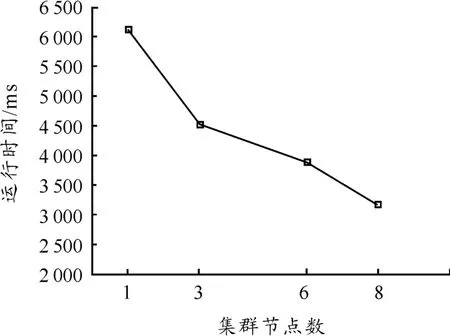
图7 遗传算法MapReduce实现方法的加速比实验结果

5 结束语

MapReduce算法模型实现粗粒度并行遗传算法是通过不同的子种群各自独立地进行，把每次进化找到的当前最优解分配到各个子种群中去，以促进其他子种群的进化。采用该方法可以选取和保留每个子群的优秀个体，在保持优秀个体进化稳定性的同时，加快进化速度，避免单种群进化过程中出现的过早收敛现象。

［1］胡晨骏，王晓蔚.基于多核集群系统的并行编程模型的研究［J］.计算机技术与发展，2008，18(4):70－74.

［2］Apache Hadoop.Hadoop［EB/OL］.［2011 － 02 － 15］.http://hadoop.apache.org.

［3］Tom White，Hadoop.The.Definitive.Guide，OReilly Yahoo Press，2ndedition，2009:175 －186.

［4］Goldberg D E.Genetic Algorithms in Search，Optimization＆ Machine Learning［J］.Addison Wesley，Reading，1989.

［5］周明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999:68－112.

［6］Corcoran A L，Wainwright R L.A Parallel Island Model Genetic Algorithm for the Multiprocessor Scheduling Problem［C］//Proceedings of the 1994 ACM/SIGAPP Symposium on Applied Computing.USA:ACM Press，1994:483－487.

［7］Erick Cantú-Paz.A Survey of Parallel Genetic Algorithms［J］.Calculateurs paralleles，reseaux et systems repartis，1998.

［8］Jimmy Lin，ChrisDyer.Data-Intensive Text Processing with MapReduce［J］.Morgan ＆ Claypool Publishers，2010:26－28.