正交多项式的图形及检索程序

张 楠，杨 彩

(1.重庆师范大学物理与电子工程学院，重庆 401331;2.南阳师范学院计算机科学与技术学院，河南南阳 473061)

正交多项式有着较长的研究历史，在理论上已经比较成熟。它与数学、物理以及其他科技领域都有着密切的联系，特别是在数学物理方程和逼近论以及工程技术的一些学科上有着重要的应用。

在通常的数学物理方法教材或工具书中已经给出了正交多项式的一般表达式、母函数、递推公式、正交归一性等，但大都是以级数形式给出的，这往往会导致计算量过大。本文利用数学物理方法的相关理论，根据最低阶几个正交多项式的值及其递推公式，编写计算机高级语言程序，计算出随宗量变化的正交多项式各点的值，用origin软件画图，给出这几种正交多项式的曲线和数据表，并以数据表为库文件，用Java EE框架中Struts2技术和Java SE中的随机读取文件类对库文件进行访问和检索，使正交多项式的使用更加方便。

1 正交多项式表达式及其递推公式

1.1 勒让德多项式

n 阶勒让德多项式［1－3］在区间［1，1］上的级数形式为

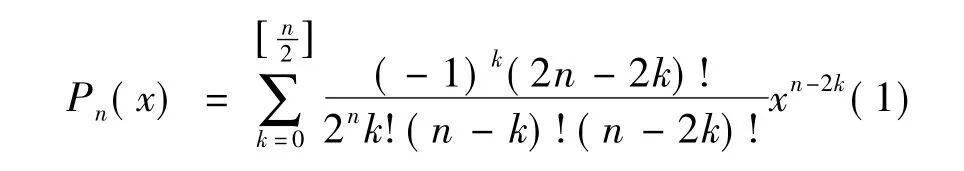
勒让德多项式的递推公式为

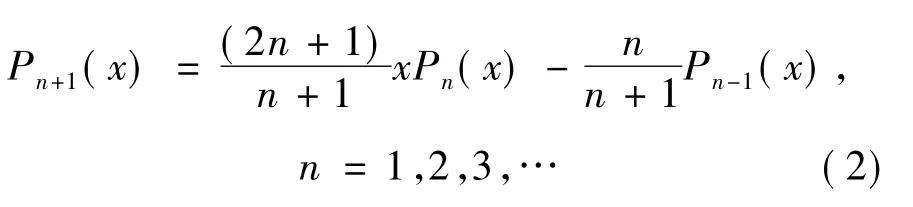
利用递推公式，由P0(x)和P1(x)可以求出P2(x)，由P1(x)和P2(x)可以求出P3(x)，以此类推，就可以求出各阶勒让德多项式的值。

1.2 拉盖尔多项式

n阶拉盖尔多项式［4］的表达式为

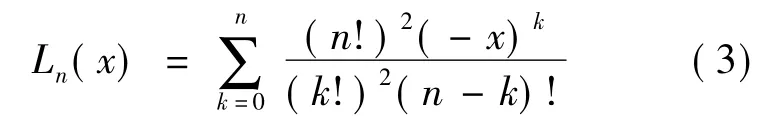
由此，最低阶的几个拉盖尔多项式的具体表达式是:

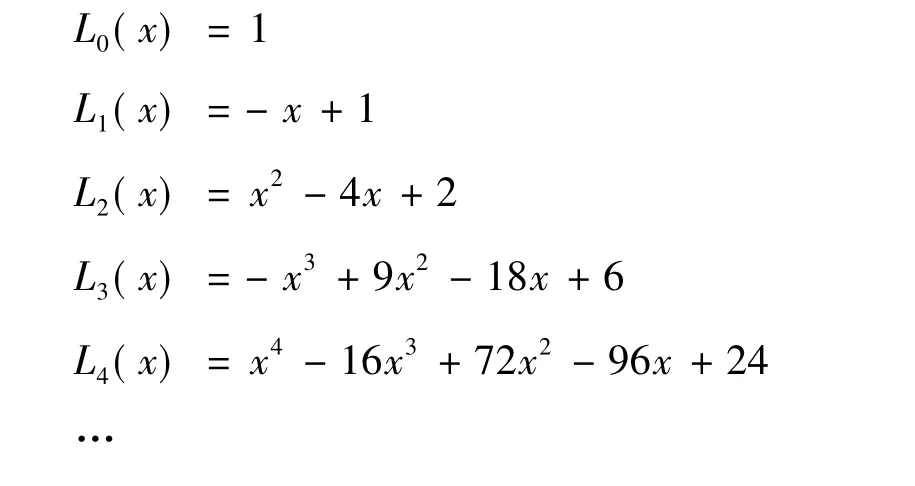
则拉盖尔多项式的递推公式为

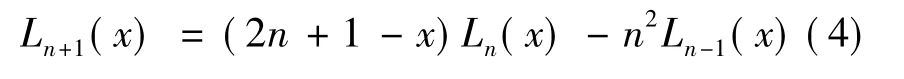
1.3 厄米多项式

厄米多项式［5，6］的表达式为

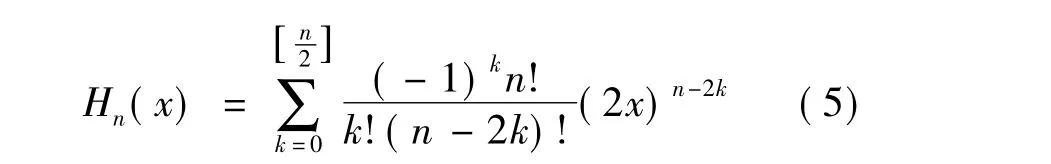
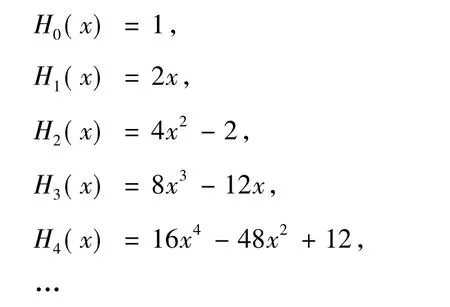
则厄米多项式的递推公式为

2 正交多项式曲线

由此根据正交多项式的表达式，从最低阶的2个正交多项式的值及其递推公式出发，编写Fortran语言［7－9］程序，计算出这些正交多项式在宗量范围内各个点的值，并用 origin［10，11］给出正交多项式曲线，如图1～4所示。

图1 P0(x)－P5(x)的图像

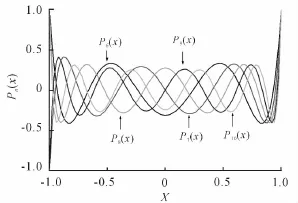
图2 P6(x)－P10(x)的图像

图3 L0(x)－L4(x)的图像

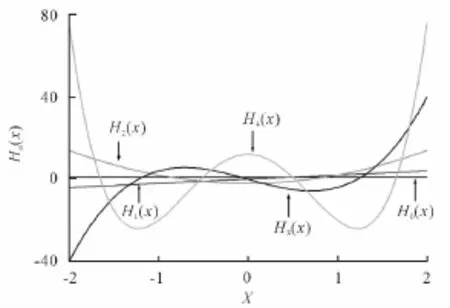
图4 H0(x)－H4(x)的图像

3 正交多项式检索程序

用Fortran语言程序计算出的多项式数据表的数据量非常大，查询起来不方便。因此，本文将数据表当作库文件，运用 Java EE框架［12］中的Struts2技术对库文件进行访问，并用Java SE［13］中的随机读取文件类进行检索，做成正交多项式检索程序，以方便查询各阶多项式的值。

检索程序的使用方法为:首先选择多项式类型，然后根据宗量x的取值范围及步长，输入宗量x的值，最后输入阶数n的值，点击“确定”即得到要求的n阶多项式的值。

具体检索示例如下:

1)求宗量x等于0.11时，5阶勒让德多项式的值。

先从多项式类型中选择勒让德多项式，根据宗量x的取值范围及步长，输入宗量x的值0.11，输入阶数n的值5，如图5所示。

图5 求解勒让德多项式值的输入界面

再点击“确定”即可得要求的5阶勒让德多项式的值，点击“返回”可继续求其它值，如图6所示。

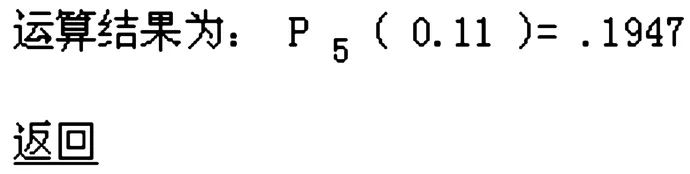
图6 勒让德多项式值的求解结果

2)求宗量x等于5.23时，12阶拉盖尔多项式的值。

先从多项式类型中选择拉盖尔多项式，根据宗量x的取值范围及步长，输入宗量x的值5.23，输入阶数n的值12，如图7所示。

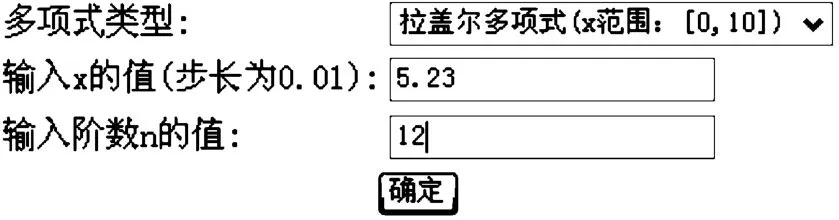
图7 求解拉盖尔多项式值的输入界面

再点击“确定”即可得到要求的12阶拉盖尔多项式的值，点击“返回”可继续求其它值，如图8所示。

图8 拉盖尔多项式值的求解结果

4 结束语

本文利用数学物理方法的基本理论，根据最低阶几个正交多项式(勒让德多项式、拉盖尔多项式和厄米多项式)的值及其递推公式，编写Fortran语言程序，计算出随宗量变化的正交多项式各个点的值，用origin给出曲线，并用Java EE框架中的Struts2技术对库文件进行访问和Java SE中的随机读取文件类进行检索，编成多项式检索程序，从而得出求各阶正交多项式值的简单方法。

［1］梁昆淼.数学物理方法［M］.3版.北京:高等教育出版社，1998:222 －412.

［2］孙慧娟.正交多项式的一些现代发展［J］.广西师范大学硕士学位论文，2010:10－58.

［3］四川大学.高等数学(第四册)［M］.2版.北京:高等教育出版社，1985:330－400.

［4］杨秀雯，梁立华.数学物理方程与特殊函数［M］.天津:天津大学出版社，1985:12－69.

［5］吴崇试.厄米多项式的定义及其他［J］.大学物理，2010，29(3):14 －15.

［6］王帮美，胡先全.简谐振子波函数的代数解及Hermite多项式的递推［J］.重庆师范大学学报:自然科学版，2009，26(3):119 －122.

［7］李立本.计算物理导论［M］.北京:中国农业大学出版社，2005:1－80.

［8］井孝功.计算物理［M］.长春:吉林大学出版社，2001:296－319.

［9］谭浩强，龙耀庭.Fortran77科学计算子程序汇编［M］.北京:清华大学出版社，1993:133－143.

［10］郝宏伟，施光凯.Origin 6.0 实例教程［M］.北京:中国电力出版社，2000.

［11］杨冰，闫循领.特殊函数教学中Matlab绘图功能的应用［J］.科技信息，2009:419－42.

［12］杨武，刘贞.Java编程及应用［M］.北京:高等教育出版社，2004:11－151.

［13］埃史尔，陈昊鹏.Java编程思想［M］.4版.北京:机械工业出版社，2007:60－94.