采用联合多因子分析法的经济发展研究
罗国旺,付馨雨
(重庆师范大学数学学院,重庆 401331)
通过研究可以发现:目前对经济发展做评价分析的方法主要有聚类分析法、主成分分析法、因子分析法[1-2]以及结合聚类分析和因子分析的方法等。比如,周介铭等的《四川省城市化发展的综合分析》[3]、王韵的《重庆市各区县经济发展的评价》[4]等采用主成分分析法;李国荣等的《我国各地区经济发展的综合评价分析》[5]、杨吉斌等的《基于因子分析的新疆主要城市发展状况评价》[6]等采用因子分析法;也有联合多种方法做评价分析的,例如臧忠卿的《贵州省县域经济发展水平的多元分析模型及应用》[7]等采用聚类分析和因子分析方法。这些已有的评价分析方法较为单一、绝对,且研究结果大都仅限于评价和排名,绝大多数研究的范围偏重于横向分析(即截面数据分析)而缺乏纵向分析(即时间序列数据分析),因此评价较为片面。也有学者开展了纵向评价分析研究,比如兰代萍等的《四川省城市化进程因子分析》[8]就是用因子分析法对四川省10年里的城市化进程进行评价分析。但该方法也存在一定的不足:没有结合横向的角度进行评价分析;采用的方法单一,且分析角度也较为狭窄。
本文在因子分析法的基础上建立了一套综合研究方法,即联合因子分析法。以西部10个地区(省、自治区、直辖市)作为研究对象,选取比较有代表性的7个经济指标,并以《中国统计年鉴》的有关数据作为基础。采用多联合因子分析法对这10个地区(省、自治区、直辖市)做实证研究,分析西部经济发展产生内在差距的原因以及经济发展在一段时间内的基本情况,从而进一步对经济发展做出合理评价,为今后制定经济发展的决策提供量化的依据。本文所建立的基于联合因子分析法的经济发展状况模型不仅能弥补前人在经济评价方法上的不足,而且能研究各地区经济在某一时间段内的横向和纵向发展状况。以2004—2011年西部10个地区(省、自治区、直辖市)8年的经济发展状况为研究对象,得出横向经济产生差距的因子、各自纵向经济发展的拉动力因子以及8年的纵向经济发展走势图。最后,结合横向和纵向做联合对比分析,对2011年西部各地区经济发展状况做出合理的评价分析。
1 地区经济发展的联合多因子分析理论模型
1.1 因子分析理论
因子分析(factor analysis)在1904年由CharlesSpearman首先提出[9],是主成分分析法的推广和深化。该方法将具有错综复杂关系的变量(或样品)综合为数量较少的几个因子,其基本思想是:根据相关性大小对变量分组,使同组内变量之间的相关性较高,而不同组间变量的相关性较低;试图用较少个数的公共因子的线性函数和特定因子之和来表达原来观测的每个变量,以达到合理地解释原始变量间的相关性和简化变量维数的目的[10]。具体步骤为:设有n个样品,每个样品有m个观测值,原始数据形式为矩阵 v=(v1,v2,…,vm)。①将原始数据进行标准化。②计算系数相关矩阵R,并对R进行主成份分析。③ 求R的特征根 λ1,λ2,…,λp(λ1≥λ2≥…≥λp≥0),以及相应的特征向量 a1,a2,…,ap。确定 p的方法有2种,可以根据特征值的大小来确定(一般取大于1的特征值),也可以用累计方差贡献率来确定(一般累计方差贡献率应在80%以上)。④求m个公共因子的载荷矩阵 A(A=[aij]m×p=[uij]m×p)。在实际分析时,为了对公共因子变量的含义有比较清楚的认识,往往对A进行极大化旋转,使得每个公共因子上的最高载荷变量的数目最少。⑤计算各公共因子的得分fi。因子变量确定后,就可以计算每一个样本的p个公共因子得分。由于误差的存在,各因子得分计算须用各种不同的方法进行估计,比如回归法、Bartlett法等。⑥ 计算综合评价指标值因子,得分依据如下:

1.2 联合多因子分析模型
本文所研究的联合多因子分析法模型是建立在因子分析的基础上,结合纵向和横向(即横截面数据和时间序列数据)分析的联合方法对所研究的对象进行因子分析,该方法能进一步对研究对象进行更深层次的了解和分析,找出所研究对象的内部变量之间的关系。
联合多因子分析的步骤如下:①建立指标体系,设研究对象集为 S={St1,St2,…,Stn},指标集为V={V1,V2,…,Vm}。② 对研究对象进行横向(即横截面数据)因子分析。S通过横向(即横截面数据)因子分析,得出对象集 S的 kt个因子(kt≤m)以及每个对象集的因子得分分别为yt1,yt2,…,ytn。其中,t表示时间点,可以通过对象集的因子得分情况对 S={St1,St2,…,Stn}进行排序和评价。③ 对研究对象进行纵向(时间序列数据)因子分析。对象集S经过纵向(时间序列数据)因子分析,得出每个对象集因子,即ki(ki≤m)个因子,其中i=1,2,…,n。④ 结合步骤②、③因子分析的结果进行联合因子分析,得出 St1,St2,…,Stn发展的主要拉动力因子(纵向因子)和产生Sti之间差距的因子(横向因子)。比较不同研究对象纵向(时间序列数据)因子分析的t时点相对于t-1时点的综合因子得分率,根据综合因子得分率的大小可以对不同研究对象St1,St2,…,Stn进行评价排序(这样的评价排序比直接采用t时点横向因子分析的因子综合得分的排序要公平和科学)。根据 St1,St2,…,Stn的综合因子得分率Z(t-1)→t= {12n}的大小 对横向因子和纵向因子进行综合分析,流程如图1所示。

图1 联合因子分析流程
2 联合多因子分析法的实证研究
2.1 经济发展指标体系的建立
本文选取7个指标来研究各地区的经济发展状况以及经济发展的内在因素。GDP是衡量一个国家和地区经济发展水平的重要指标,故选取GDP作为研究经济发展的一项指标v1;居民消费水平既反映了居民的购买力水平,也反映了经济增长和发展走势,为国家制定消费、价格、工资、货币政策及进行国民经济核算提供依据,可作为一项指标v2;资产投资是一个国家(地区)经济能持续增长的力量源泉,没有资产投资,存量资产得不到更新,经济发展就会受到很严重的阻碍,故选取固定资产投资v3和新增固定资产投资v6作为经济发展指标;城镇居民人均可支配收入v4也能间接地反映一个地区的发展状况;通过居民消费价格指数(CPI)v5可用于观察和分析消费品的零售价格和服务价格的变动对城乡居民实际生活费支出的影响程度;工业总产值是一个国家(地区)经济发展的重要拉动力,也应作为一项经济发展指标v7。
2.2 经济发展的横向因子分析和纵向因子分析
以西部地区10个省(自治区、直辖市)重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆的经济发展状况作为研究对象集,即:S={St1,St2,…,Stn}={重庆(1),四川(2),贵州(3),云南(4),西藏(5),陕西(6),甘肃(7),青海(8),宁夏(9),新疆(10)},以《中国统计年鉴2005~2012》数据为依据,以2004年为基年,采用联合多因子分析法对这10个省(自治区、直辖市)的经济发展状况进行分析。利用SPSS软件分别对横向和纵向进行KMO和Bartlett检验[10]。计算发现:KMO值都小于0.5,Bartlett检验值都小于 0.001。因此2项检验均通过,表明因子分析方法适用,并得出表1~3所示的结果。通过式(1)可得到表4的结果;通过式(2)~(11)可算出各地区纵向综合因子得分以及综合因子得分率,如表5、图2所示。

表1 2012年横向因子分析解释的总方差和因子得分(ks=0.647)

表2 重庆(1)2004—2011年纵向因子分析解释的总方差和因子得分
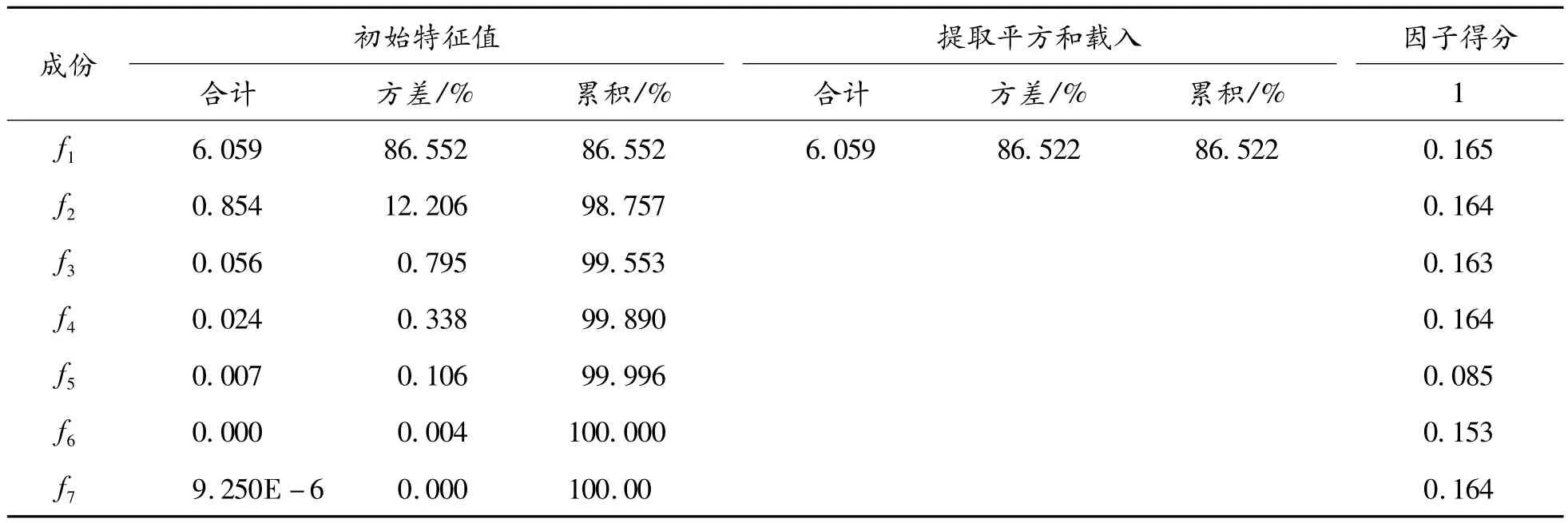
表3 新疆(10)2004—2011年纵向因子分析解释的总方差和因子得分
通过对2011年横向因子的分析,采用回归方法得到因子得分系数矩阵(略),建立因子得分函数式:
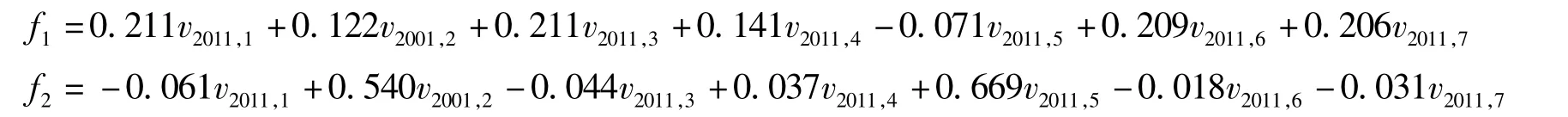
横向分析综合得分[11]的计算公式为:

通过对西部各地区进行2004~2011年纵向因子分析后得到纵向因子得分函数:
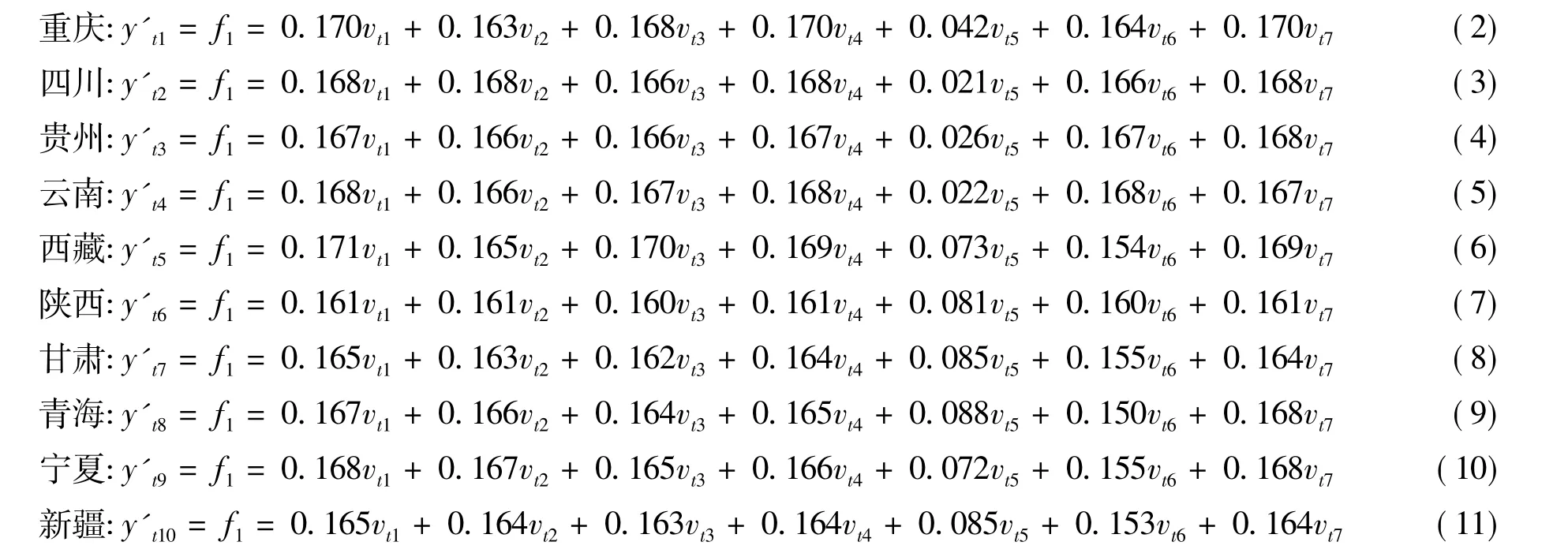
其中:式(1)~(11)中 f1的方差贡献率依次为:84.728%、84.728%、85.115%、84.731%、84.731%、83.075%、88.387%、86.590%、84.590%、84.705%、84.705%。
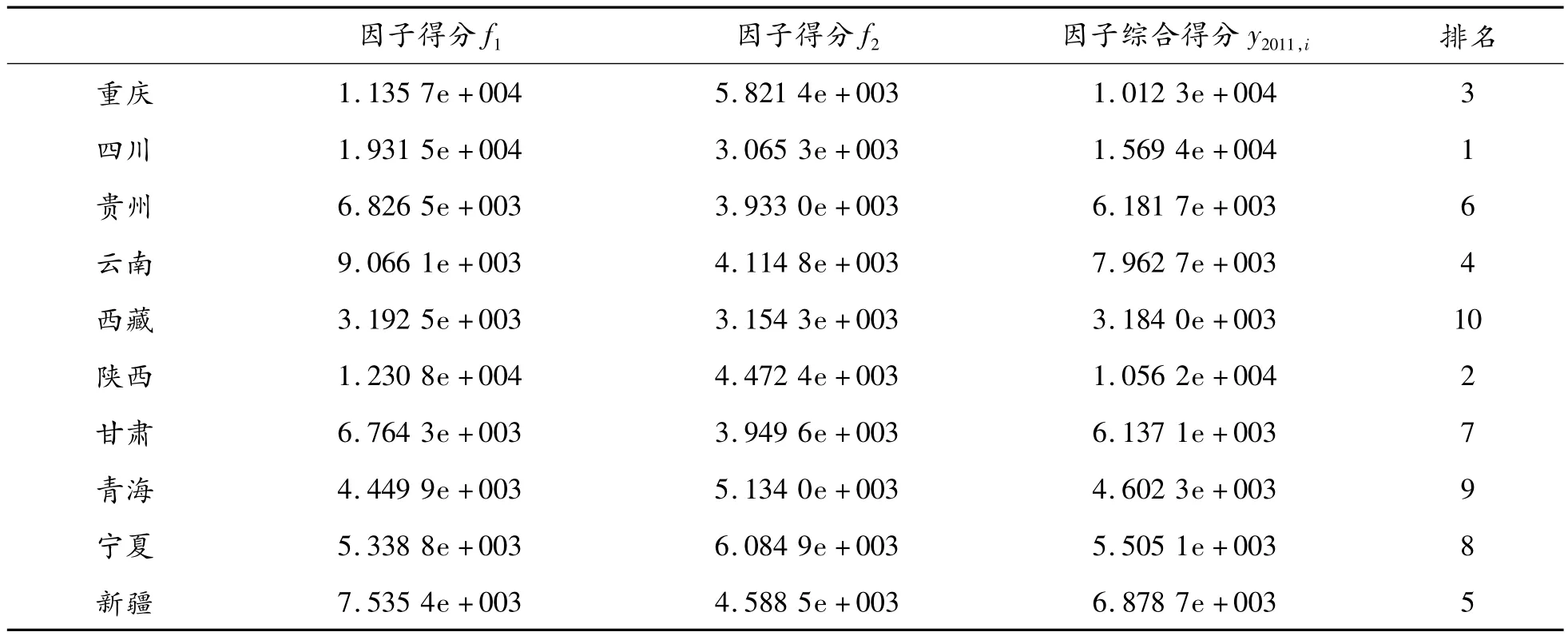
表4 西部地区2011年横向因子分析的综合因子得分及排名
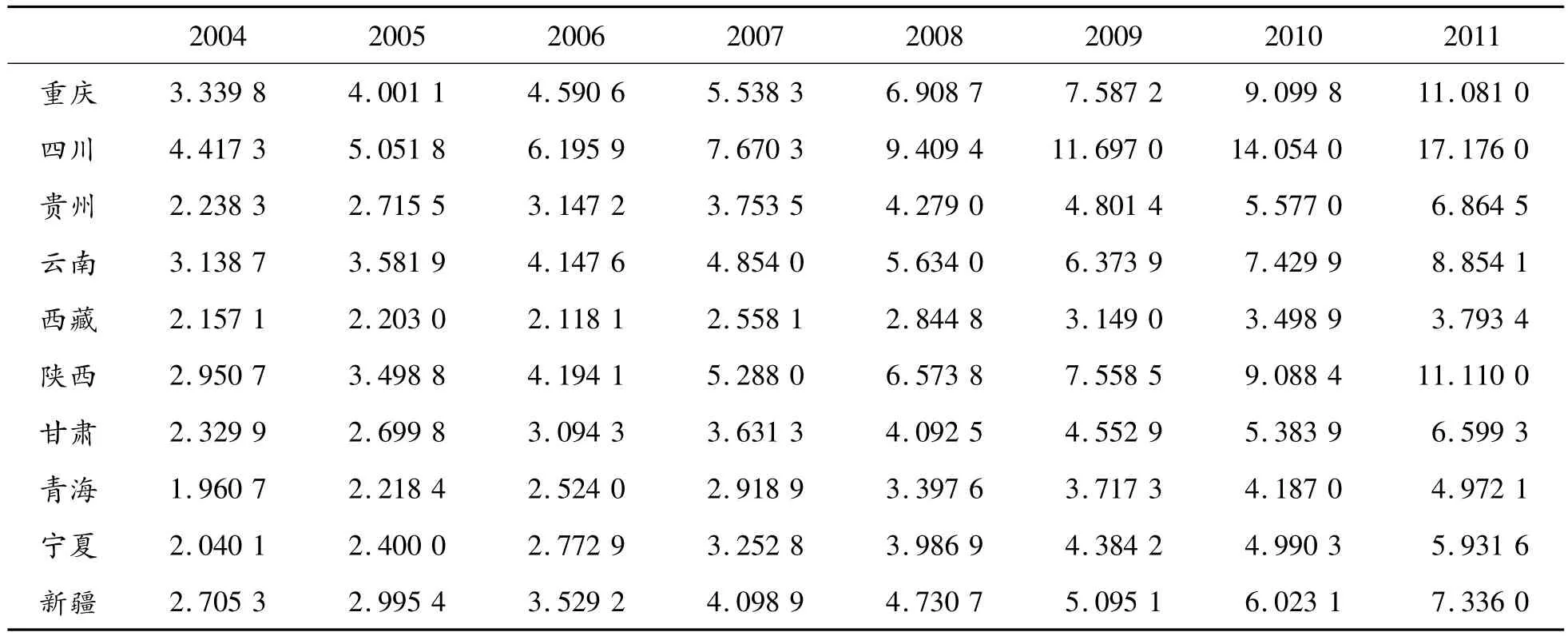
表5 各地区2004—2011年经济发展纵向因子分析的综合因子得分
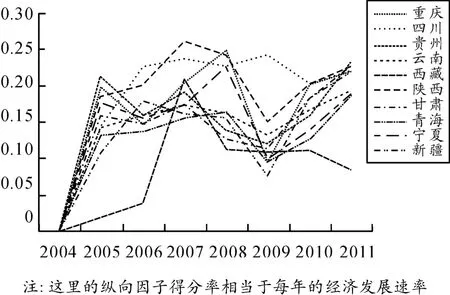
图2 纵向因子得分率
2.3 各地区经济发展状况综合评价和分析
本文结合2011年经济发展的横向因子分析和后7年的纵向因子分析对2011年西部10个地区经济发展状况进行综合评价。通过式(12)计算出各地区的横向和纵向综合总得分如表6所示。发现:原来按2011年横向因子分析得到总分排名第6的贵州,现在排名为第5,因此有必要对经济发展进行横向和纵向综合分析。

式中,w1,w2为权重,且 w1+w2=1(w1,w2通过AHP 方法得到,即 w1=0.33;w2=0.67),y″ti和分别为标准化后的值。
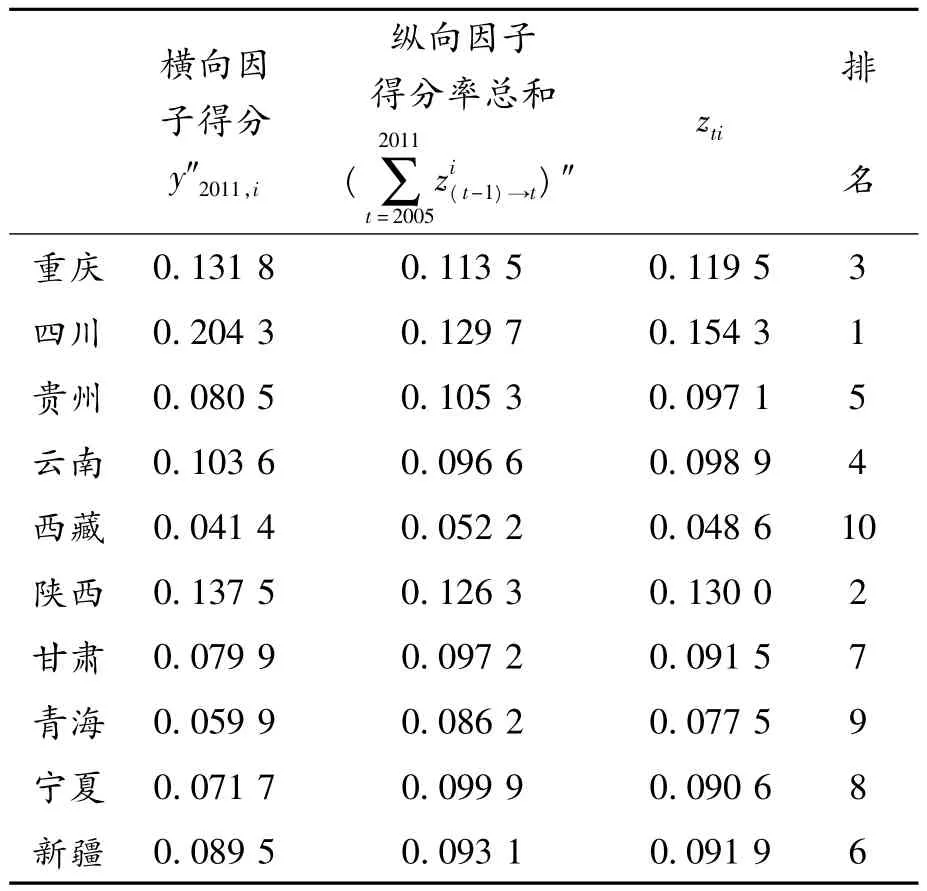
表6 基于横纵联合分析的2011年西部地区经济发展状况
3 结束语
本文建立的联合因子分析法的模型不仅能弥补前人在经济评价方法上的不足,而且能对各地区在某一时间段的横向和纵向发展状况进行分析。选取2004—2011年西部10个省(自治区、直辖市)8年的经济发展状况作为研究对象,得出各地区在该段时间的因子得分率,可直观地看出每个地区在这8年里的经济发展状况,从而能对各地区的经济发展状况做出确切的分析和评价。本文的研究为今后的经济发展状况评价提供了量化依据。然而,由于经济发展所涉及的指标不仅限于本文所选的7项,因此可在后续的工作中加入其他指标开展进一步研究。
[1]刘林军,吴黎军.基于因子分析的我国西部12城市经济发展状态实证分析[J].重庆理工大学学报:自然科学版,2010,24(11):118 -122.
[2]曾国平,王正攀,曹跃群.西部基本公共服务水平地区差异的实证分析[J].重庆理工大学学报:社会科学版,2011,25(11):36 -44.
[3]周介铭,彭文甫.四川省城市化发展的综合分析[J].四川师范大学学报:自然科学版,2004,27(5):527-528.
[4]王韵.重庆市各区县经济发展的评价[J].重庆师范大学学报:自然科学版,2012,29(2):105.
[5]李国荣,马敏娜.我国各地区经济发展的综合评价分析[J].统计观察,2009(27):92.
[6]杨吉斌,韩萍.基于因子分析的新疆主要城市发展状况评价[J].新疆师范大学学报:自然科学版,2009,28(3):65.
[7]臧忠卿.贵州省县域经济发展水平的多元分析模型及应用[J].数学的实践与认识,2007,37(5):26 -28.
[8]兰代萍,谢贤健,胡学华.四川省城市化进程因子分析[J].内江师范学院学报,2010,25(4):72.
[9]于秀林,任雪松.多元统计分析[M].北京:中国统计出版社,1999.
[10]卢纹岱.SPSS for Windows统计分析[M].北京:电子科技出版社,2003.
[11]林海明,张文霖.主成分分析与因子分析的异同和SPSS软件[J].统计研究,2005(3):66-69.

