高速铁路平纵断面关键点处的轮轨振动特性

杨久川，王开云

(西南交通大学牵引动力国家重点实验室，成都 610031)

随着高速铁路运营速度的不断提高，车辆与线路之间的动力相互作用显著增强，尤其是当车辆高速通过缓和曲线起(止)点、竖曲线起(止)点等线路平纵断面关键点时，其动力作用更加明显，严重影响了车辆运行安全性和旅客乘坐舒适度。因此，分析高速行车条件下平纵断面关键点处的轮轨振动特性，可为高速铁路设计参数的选取和线形优化提供理论依据。然而传统的线形参数分析方法大多为静态或准静态［1－3］，极少考虑车辆和线路的动态相互作用。因此，国内外陆续展开了基于动力学理论的线形参数研究［4－7］。在此背景下，本文运用多刚体系统动力学的分析方法进一步研究线路平纵断面关键点处的轮轨振动特性。

1 仿真计算模型

1.1 高速车辆模型

高速列车分为动力集中式和动力分散式2种，其中以动力分散式作为主要的发展方向。动力分散式高速列车可区别为动车和拖车2种，通常可简化为由车体、前后转架和4个轮对组成的多刚体系统。本文以国产某型动车组为原型，基于多刚体系统动力学理论，建立参数化的车辆模型。模型的自由度和拓扑关系如图1所示。

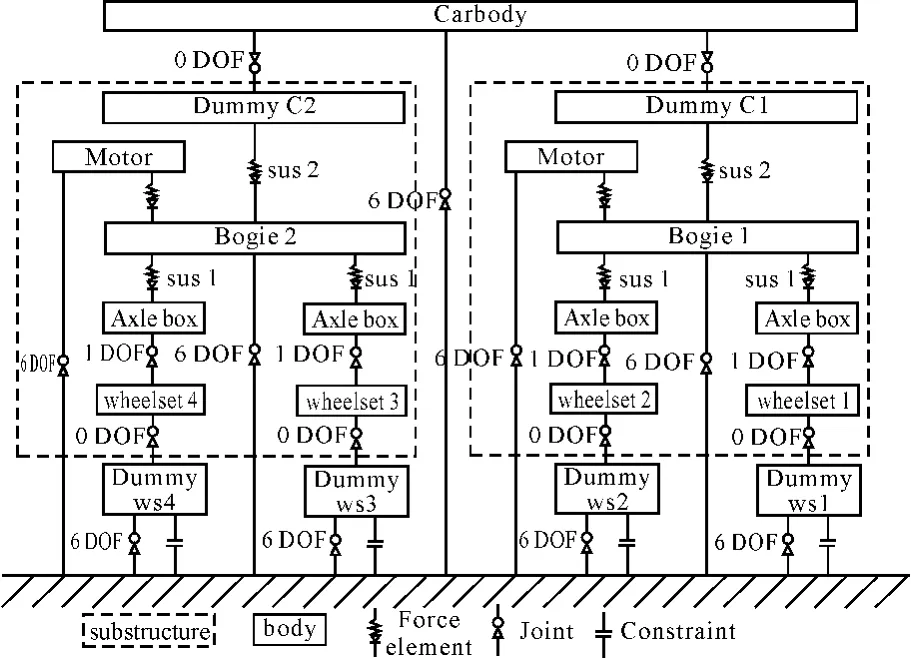
图1 高速车辆模型拓扑关系

1.2 高速铁路线形

本文以设计最高行车速度为350 km/h的高速铁路为研究对象。依据现行高速铁路设计规范［8］，不同速度等级的线路允许的最小曲线半径不同。因此，表1给出了设计最高行车速度为350 km/h线路的曲线半径、设计超高、缓和曲线长度。针对不同的曲线半径，设计超高依据线路的均衡超高折中选取，缓和曲线长度按照3种舒适度条件计算得出，依次为优秀、良好、一般。

为保证车辆在变坡点处的运行安全性和旅客乘坐的舒适度要求，当相邻坡段坡度差大于等于1‰时，均需采用圆曲线型竖曲线连接。对于不同设计速度等级的线路，现行高速铁路设计规范规定的最小竖曲线半径如表2所示，其依据为人体感知的惯性离心加速度限值。试验结果及国内外运营经验显示，这一加速度限值一般为0.4 m/s2，困难条件下为0.5 m/s2。

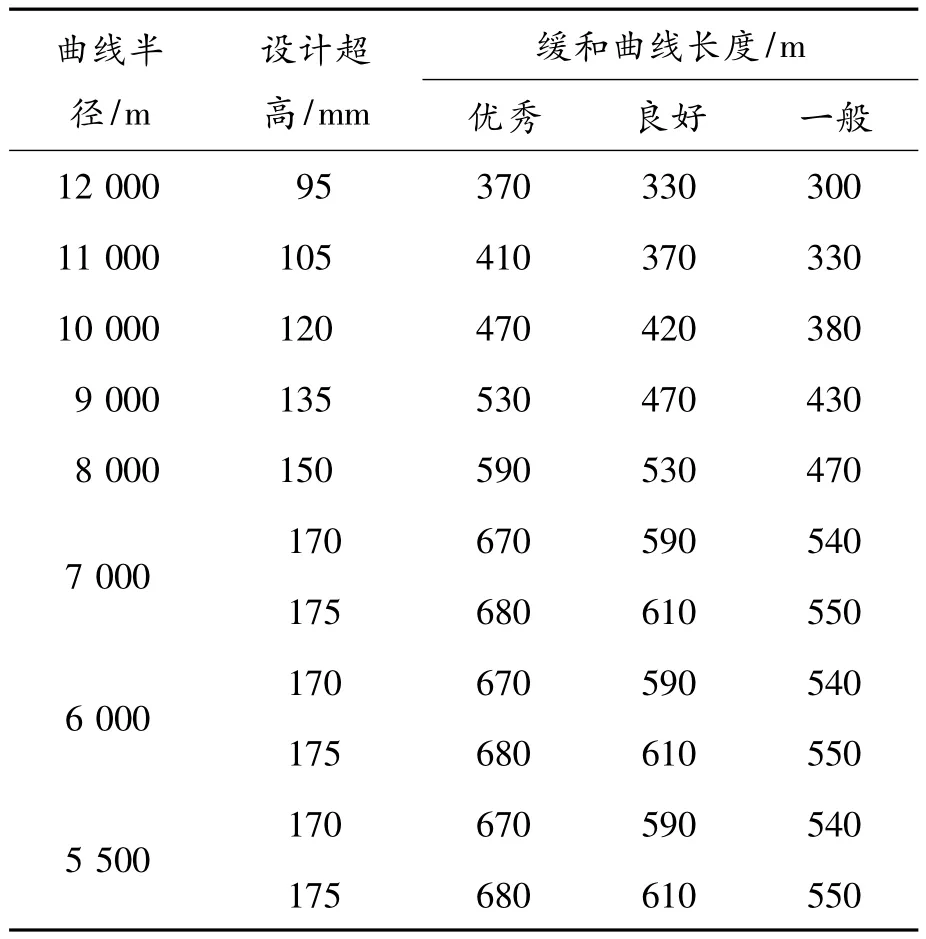
表1 速度等级为350 km/h线路的线形参数

表2 高速铁路设计规范规定的最小竖曲线半径

2 缓和曲线长度对轮轨振动的影响

现行高速铁路设计规范中给出的3种缓和曲线长度，其计算依据是缓和曲线超高时变率限值允许的舒适度条件仅满足静态舒适度要求。本节从动力学的角度出发，采用数值仿真计算方法进一步检算缓和曲线长度对轮轨振动的影响，尤其注意缓和曲线起(止)点处的轮轨振动情况。

通过统计国内某条高速铁路曲线半径的使用情况，发现其中以8 000～10 000 m为常用曲线半径。因此，本文以半径8 000 m、超高150 mm的线路为例，仿真计算缓和曲线长度分别为470、530、590 m的轮轨动力相互作用，得到如图2、3所示的轮轨力时程曲线。

通过分析图2、3可知:轮轨横向力和垂向力均在出缓和曲线的终点附近取得最大值，而且缓和曲线越短，轮轨横向力和垂向力均越大。例如:在图2中，当缓和曲线长度分别为590、530、470 m时，轮轨垂向力最大值为依次为 66.40、72.84、76.54 kN;在图3中，轮轨横向力最大值依次为0.54、1.62、2.82 kN。

由此可知，缓和曲线长度影响轮轨振动主要表现为:缓和曲线越短，缓和曲线起(止)点处的轮轨振动越剧烈，且在出缓和曲线终点处取得轮轨横向力和垂向力的最大值。

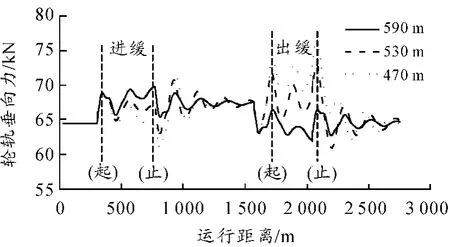
图2 不同缓和曲线长度时的轮轨垂向力时程曲线

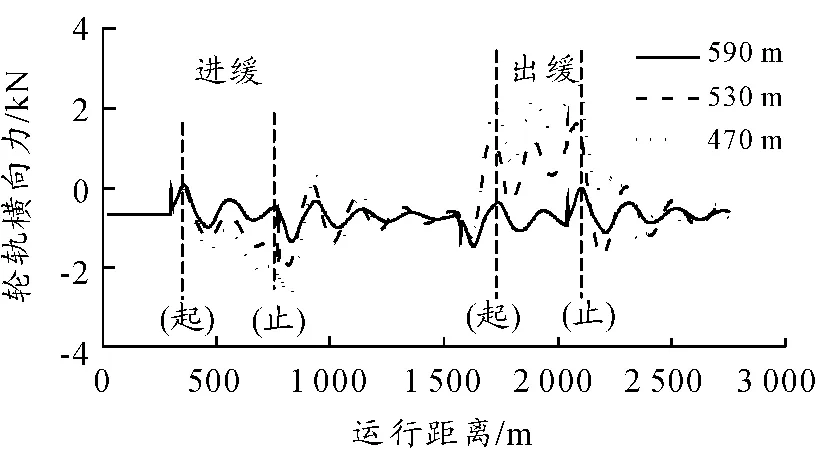
图3 不同缓和曲线长度时的轮轨横向力时程曲线

3 竖曲线半径对轮轨振动的影响

竖曲线用于连接相邻两坡段。当车辆运行通过圆曲线型竖曲线时，轮轨动态相互作用既包含有圆周产生的惯性离心力，又叠加有竖曲线起(止)点处的轮轨冲击力。其中，惯性离心力可由牛顿力学计算得到，而轮轨冲击力必须采用数值计算方法求出。因此，本文基于多刚体系统动力学，仿真分析不同竖曲线半径对轮轨动力作用的影响情况。

仍以设计最高行车速度为350 km/h的线路为例。考虑凹、凸形竖曲线的不同，利用数值仿真得到不同竖曲线半径时的轮轨垂向力及车体垂向加速度值。现以竖曲线半径为25 km的线路为例，给出轮轨垂向力和车体垂向加速度时程曲线，如图4、5所示。由仿真结果可知，轮轨垂向力和车体垂向加速度最大值均出现在竖曲线的起点处。

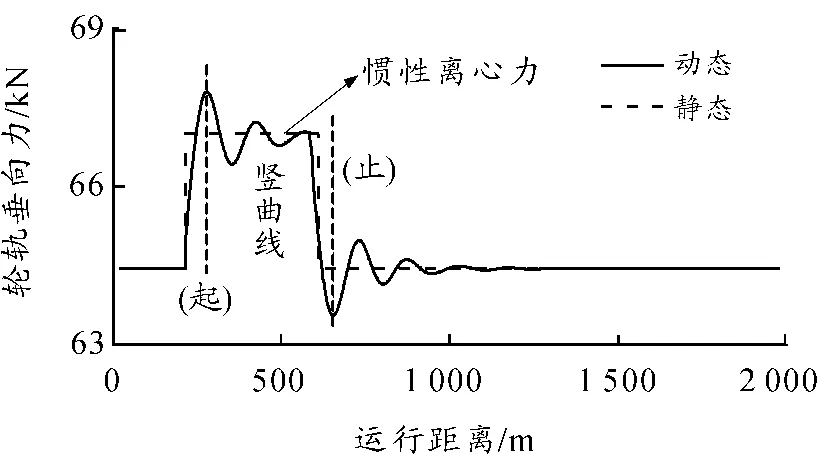
图4 竖曲线半径为25 km时的轮轨垂向力时程曲线

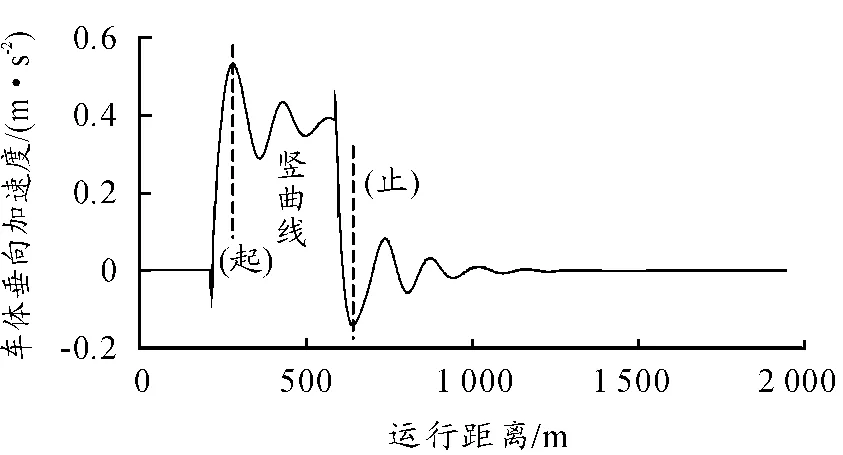
图5 竖曲线半径为25 km时的车体垂向加速度时程曲线

进一步统计不同竖曲线半径时的轮重变化量和车体垂向加速度最大值，所得结果见图6、7。

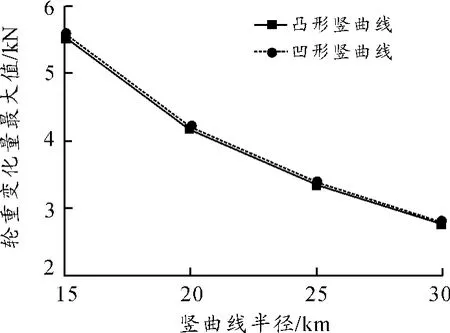
图6 不同竖曲线半径时的轮重变化量最大值

图7 不同竖曲线半径时的车体垂向加速度最大值

由图6、7可知:无论凹形或凸形竖曲线，轮重变化量和车体垂向加速度的最大值均随竖曲线半径的增大而减小，且减小的幅度近似线性。例如:当竖曲线半径为20 km时，凹、凸形线路的轮重变化量最大值均接近4.2 kN，车体垂向加速度最大值均为0.65 m/s2;当竖曲线半径增大到30 km时，轮重变化量最大值减小为2.7 kN，车体垂向加速度最大值减小为0.44 m/s2。由图7进一步可知:当竖曲线半径为25 km时，车体的垂向加速度超过了0.5 m/s2的人体感知加速度限值。由此可知，基于多刚体系统动力学的计算结果略大于表2所示的最小竖曲线半径。

4 结论

1)缓和曲线越短，缓和曲线起(止)点处的轮轨振动越剧烈，且在出缓和曲线终点上取得轮轨横向力和垂向力的最大值。

2)竖曲线起(止)点处的轮重变化量和车体垂向加速度随竖曲线半径的增大近似线性减小，且与竖曲线的线形凹、凸性无关;针对设计最高行车速度为350 km/h的线路，当竖曲线半径为25 km及以下时，车体垂向加速度已超过人体感知离心加速度限值，无法旅客乘坐的舒适度要求。

［1］易思蓉.铁路选线设计［M］.成都:西南交通大学出版社，2005.

［2］何华武，刘增杰.既有线提速200 km/h平纵断面技术标准研究与验证［J］.铁道学报，2007，29(2):64－70.

［3］龚增进，冯毅杰.客运专线无砟轨道线路平纵断面主要技术参数的研究［J］.铁道工程学报，2007:170－173.

［4］YANG J C，WANG K Y.Characteristic of Wheel-Rail vibration of Vertical Section in High-speed Railway ［J］.Journal of Modern Transportation，2012，20(1):10 －15.

［5］LONG Xu-you，WEI Qing-chao，SHI Jin，et al.Dynamic analysis and ride comfort evaluation of track alignment for high speed railway［C］.Beijing:Key Technologies of Railway Engineering，2010.

［6］LONG Xu-you，WEI Qing-chao，ZHENG Fang-yuan.Dynamic analysis of railway transition curves［J］.Proceeding of the Institution of Mechanical Engineers，Part F，Journal of Rail and Rapid Transit，2010，224(1):1 －14.

［7］周志华，向俊.广珠城际铁路平纵断面设计参数动力学评估［J］.铁道科学与工程学报，2009，6(5):21－25.

［8］TB 10020—2009高速铁路设计规范［S］.北京:中华人民共和国铁道部，2009.