基于插值和加窗傅里叶变换的曲率模态提取算法

杨 翀，FU Yu，朱长春，田光明

(1.中国工程物理研究院总体工程研究所，四川绵阳 621900;2.Temasek Labs and School of MAE，Nanyang Technological University，50 Nanyang Drive，Singapore 637553，Singapore)

裂纹的出现和扩展会造成结构的性能下降甚至破坏，因此对早期裂纹的位置进行检测是工程实践中的一个重要课题。裂纹的出现会影响结构的物理特性，例如质量、阻尼和刚度等，进一步会导致结构振动参数发生改变。通过测量这些振动参数的改变可以对裂纹进行检测［1］。常见的基于振动测量的裂纹检测方法主要有频率法和模态法。频率法通过测量结构固有频率的改变来检测裂纹，其优点是测量方法简单和精度高，但其缺点也比较明显。裂纹导致的固有频率改变量较小，因此更容易受到其他因素(如环境温度、加载精度等)的影响，而且，固有频率的变化受到裂纹位置和开裂程度的共同作用，不同的裂纹位置和开裂程度可能产生相同的变化量，特别是在对称结构中，对称位置上的同等裂纹就能引起相同的变化量。这都给裂纹的定位带来困难。模态法则避免了这些问题。不过模态的测量比较复杂，需要一系列的传感器，而且通常传感器的分布不可能非常密集，这就导致测量的空间分辨率和精度较低。另一方面，模态法中更常见的是通过对曲率模态，即对位移模态2阶导数的比较来检测裂纹，因为其效果更好［2］。曲率模态通常采用中心差分法计算，在模态测量的分辨率和精度不高时往往得到的曲率模态误差很大，无法用于裂纹检测。针对这一问题，本文引入了插值和加窗傅里叶变换算法来计算曲率模态。采用自同步的多点多普勒测振仪对完整梁和裂纹梁进行实验，准确地探测到了裂纹所在位置。实验结果表明该算法具有很高的精度。

1 曲率模态提取算法

插值法是一种通过计算在采样点之间建立一些新的点，从而提高分辨率的数值方法。常见的插值算法有线性插值、多项式插值和样条插值等。线性插值方法简单，但精度低。样条插值精度较高，但须引入边界条件，而且由于测量点通常不会落在边界上，因此在模态的样条插值重建时边界的精度较低。多项式插值法在采样点数量较多时，边界会出现龙格现象而导致误差较大。龙格现象可以采用分段插值如分段Hermite插值等方法解决。本文采用分段三次Hermite插值方法。

加窗傅里叶变换(windowed Fourier transform，WFT)在时间信号分析领域被称为短时傅里叶变换。WFT将信号乘以一个有限窗口再进行傅里叶变换，从而得到窗口内信号的频率信息。窗口逐渐移动，则可以得到信号在不同位置(时间)处的局部频率信息。最常用的窗口是高斯窗。信号f(x)的WFT可表示为

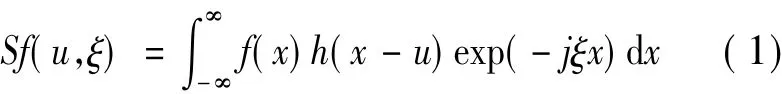
基于 WFT，Qian［3］提出了一种用于光学干涉条纹图位相提取的加窗傅里叶脊(windowed Fourier ridges，WFR)算法。加窗傅里叶脊是指针对某个u值振幅谱|Sf(u，ξ)|的最大值，此时对应的频率ξ被近似认为是信号的当地频率。对一个形如f(x)=B(x)exp{jφ(x)}的复信号，WFR 提取位相φ(x)和位相导数φ'(x)的算法可由式(2)表示。

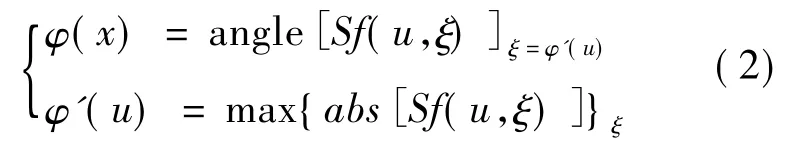
选择合适的窗口尺寸［4］，WFR可以精确提取信号的导数。结构的模态亦可看成形如f(x)=B(x)exp{jφ(x)}的复信号，如欧拉梁在自由、固支或简支的边界条件下，其模态的解析解为双曲函数和三角函数的表达式，均可以用指数函数来表示。因此，WFR算法也适用于提取位移模态的2阶导数，即曲率模态。

2 实验验证

通过对加工完整的和含裂纹的悬臂梁进行实验验证本算法。梁的长、宽、高分别为270、10和10 mm，材料为纯铝。裂纹采用线切割加工，为张开型裂纹，相对深度(裂纹深度/梁的厚度)为0.4，位于距离悬臂梁固支端135 mm处，其相对位置(裂纹与固支端距离/梁的长度)e为0.5。由于传感器的附加质量会影响测量精度，因此本文采用了一种新的激光多普勒测振装置(laser Doppler vibrometer，LDV)［5］来对梁的模态进行非接触式测量。该测振装置采用单光源和单个光探测器，能实现多点的同步测量。测量点为14个，位于梁的中心线上，距固支端的距离分别为70+(i－1)×10 mm，i=1，2，3，…，14。实验装置及光路设置如图1所示。

测量结果如图2所示。图2中横坐标为相对位置。对LDV测量得到的梁的2阶位移模态，通过分段三次Hermite插值算法进行插值，以提高其空间分辨率，然后分别采用WFR和中心差分法提取梁的曲率模态。插值点数据依赖于实测点，因此插值法可以提高分辨率，但不能提高中心差分法的计算精度。WFR算法由于具有局域滤波的能力，可以提取更加精确的曲率模态。图3为完整梁和裂纹梁曲率模态的绝对差值。采用WFR算法，曲率模态差在裂纹位置出现明显的尖峰;而采用中心差分法，由于曲率模态的计算误差太大，无法进行裂纹定位。并且，距离裂纹最近的采样点位于e=0.481和0.520处，但裂纹定位却能精确到e=0.498，可见将插值法和WFR算法结合能大幅提高空间分辨率和检测精度。

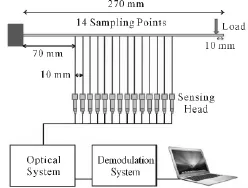
图1 实验装置及光路设置

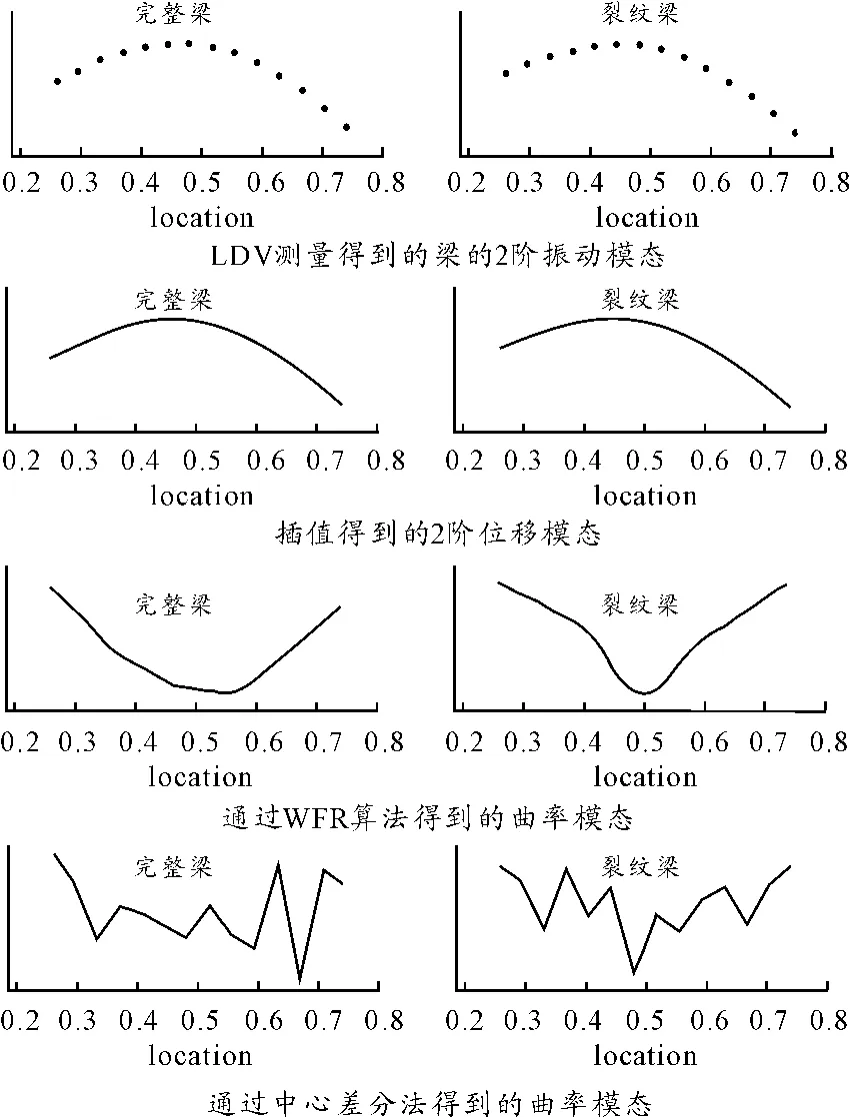
图2 完整梁和裂纹梁的模态和曲率模态对比

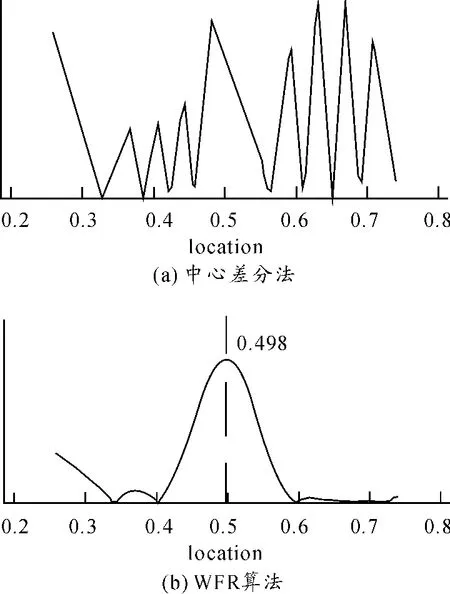
图3 采用中心差分法和WFR算法得到的完整梁和裂纹梁曲率模态差

3 结束语

本文提出了一种基于插值和加窗傅里叶变换的曲率模态提取算法。由于模态测量比较复杂，并且通常传感器的数量有限，导致测量的空间分辨率和精度较低。这种情况下，采用常见的中心差分法计算曲率模态的误差很大。本文通过插值来提高分辨率，采用加窗傅里叶变换算法提高曲率模态的计算精度。实验结果表明:该算法能精确地提取曲率模态，准确地定位悬臂梁上的裂纹位置。值得注意的是，由于插值法的精度依赖于实际采样点，因此采样本身的分辨率仍然是决定裂纹定位精度的主要因素。对于大尺度或者是高精度的测量，在测量点有限的情况下，可以采用分段检测或者多次测量逐渐缩小测量范围的方法，从而保证测量精度。

［1］Kim J T，Ryu Y S，Cho H M.Damage identification in beam-type structures:Frequency-based method vs modeshape-based method［J］.Eng Struct，2003，25(1):57 －67.

［2］Pandey A K，Biswas M，Samman M M.Damage detection from changes in curvature mode shapes［J］.J Sound Vib，1991，145:321 －332.

［3］Qian K.Two-dimensional windowed Fourier transform for fringe pattern analysis:principles，applications and implementations［J］.Opt Lasers Eng，2007，45(2):304 －317.

［4］Yang C，Lu Q，Zhao J.Window size selection in windowed Fourier transform for phase retrieval［J］.Opt Lasers Eng，2009，48(11):1096 －1103.

［5］Fu Y，Guo M，Phua P B.Multipoint laser Doppler vibrometry with single detector:principles，implementations，and signal analyses［J］.Appl Opt，2011，50(10):1280－1288.