多节点集装箱海铁联运箱位分配优化模型

刘 迪,杨华龙,张 燕

(1.大连海事大学交通运输管理学院,辽宁大连116026 2.大连交通大学交通运输工程学院,辽宁大连116028)

多节点集装箱海铁联运箱位分配优化模型

刘 迪1,2,杨华龙*1,张 燕1

(1.大连海事大学交通运输管理学院,辽宁大连116026 2.大连交通大学交通运输工程学院,辽宁大连116028)

不确定性需求下集装箱海铁联运的箱位分配优化,对联运经营人的经营效率和效益产生极为重要的影响.基于收益管理理论,结合集装箱海铁联运的经营和组织特点,充分考虑合同客户、普通客户和加急客户的不同需求,分两阶段建立了多节点集装箱海铁联运箱位分配优化模型.第一阶段为面向合同客户的协议销售箱位分配模型,第二阶段为面向普通客户和加急客户的自由销售箱位分配模型.针对第一阶段需求的相对确定性特征和第二阶段需求的随机特征,分别运用确定性线性规划(DLP)和随机线性规划(SLP)方法进行模型转化并求解.通过算例验证了上述模型与算法的适用性和有效性.

综合交通运输;箱位分配;收益管理;集装箱;海铁联运;优化模型

1 引 言

集装箱海铁联运作为综合运输体系建设中重点推进的多式联运模式,其市场需求日益增大,并呈现多样化特征,这对海铁联运经营人的运营管理提出更高的要求.集装箱海铁联运具有应用收益管理理论的典型特征[1],如何运用收益管理理论对不同的市场需求进行箱位分配,提高联运经营人的运作效率和收益水平,是关系到联运经营人未来发展的重要决策问题.

收益管理理论起源于20世纪70年代美国的航空业,40多年来已经在许多领域得到广泛应用.目前,基于收益管理的舱位分配问题仍是集装箱运输应用领域研究的热点.Ting和Tzeng[2]应用模糊多目标规划方法,以托运人满意度最大化和班轮公司收益最大化为目标,研究了班轮运输中集装箱舱位分配问题;Feng和Chang[3]研究了特定航线上考虑空箱调运成本的班轮最优舱位分配问题,建立了以班轮公司运营利润最大为目标,以船舶运力、集装箱需求和空箱供给为约束的数学规划模型; Sebastian[4]研究了考虑多航段、多航线间转运可能性的班轮舱位分配模型,并进行了班轮舱位预定的离散仿真研究,以确定班轮公司的最佳舱位预定战略;卜祥智等[5,6]研究了考虑多产品、多航段、空箱调运、长期运力合同、路径选择等因素不同组合的一系列集装箱班轮舱位分配随机规划模型,并基于需求的不确定性,应用稳健优化的方法对模型进行求解.

上述文献探讨的都是海运单一运输方式的集装箱运输收益管理,而关于集装箱海铁联运收益管理的研究较少涉及,只有作者在文献[1]中运用收益管理理论研究了集装箱海铁联运的动态定价与箱位分配综合模型,但该文献针对的仅仅是单起讫点间的集装箱海铁联运线路.另外,现有文献大多缺乏对客户分类的研究,只有文献[6]提到了合同需求和即时需求的分类.区别于上述文献,本文结合集装箱海铁联运的经营和组织特点,充分考虑合同客户、普通客户和加急客户的不同需求,针对复杂的多节点集装箱海铁联运线路,研究不确定需求下的箱位分配问题,建立基于收益管理的集装箱海铁联运两阶段客户细分的箱位分配模型,为联运经营人的运营管理提供科学的决策依据.

2 问题描述

假设某无船承运人型的联运经营人企业经营一条多节点的集装箱海铁联运线路,如图1所示.该联运线路由铁路段和海运段组成:铁路段为港口A1的内陆腹地集疏运线路,节点为集装箱办理站S1,S2,…,Sm;海运段为A端和B端之间的顺时针海运航线,A端和B端的节点为港口A1,A2,…,Aq和B1,B2,…,Bn;铁路段和海运段的衔接点为Sm和A1,假设可以在此完成铁路和海运的无缝换装.联运线路运行方向如图1中箭头方向所示.

根据集装箱海铁联运货流组织特点,铁路段任意节点(除了衔接点Sm)和海运段B端任意节点之间构成了联运重箱OD流.为了便于说明,本文定义:Ω1={S1,S2,…,Sm-1}为铁路段前m-1个节点的集合,Ω2={B1,B2,…,Bn}为海运段B端所有节点的集合,则海铁联运重箱OD流可表示为去程节点对(ij)和回程节点对(ji),∀i∈Ω1,∀j∈Ω2.整条联运线路被划分成(m+n)个区段,铁路段有(m-1)个区段,海运段有(n+1)个区段,其中从港口A1到B1可视为一个区段,为区段m.考虑到海运段各节点间的空箱调运一般由班轮公司负责,那么假设联运经营人仅负责铁路段各节点间的空箱调运,定义Ω3={S1,S2,…,Sm}为铁路段所有节点的集合,则空箱调运OD流表示为节点对(gh),∀g,h∈Ω3,当g＜h时,(gh)表示去程,当g＞h时,(gh)表示回程.

联运经营人通过与实际分承运人(某铁路公司和某班轮公司)签署长期承包协议,以较优惠的承包价获得箱位容量为Q的S1-Sm间铁路集装箱班列经营权和A端-B端间海运集装箱班轮上等量的箱位经营权.这既保证了稳定的运力资源,又降低了经营成本.假设箱位容量Q和经营成本在承包协议期内都是固定不变的.在协议期内,联运经营人以契约承运人的身份向货主销售箱位并收取全程运费,组织集装箱海铁联运.

集装箱海铁联运的箱位销售过程可以分为两个阶段:第一阶段联运经营人根据大客户的请求,以较低的协议运价将一部分箱位提前销售,表现为一系列的销售合同;第二阶段联运经营人对剩余的箱位进行自由销售,给出公开报价,并接受各种零散客户的预订.

在第一阶段中,由于合同客户的联运运价和空箱调运单位成本都是确定的,所以,联运经营人需要决策的就是按照协议运价和空箱调运运费率,各重箱OD节点对上应该预留多少箱位给合同客户及如何调运空箱,以满足合同客户和空箱调运需求,使收入最大化.

在第二阶段中,大多数零散客户会在发班前的1-2周按照公布的运价提前预订箱位,这类客户被称为普通客户;而少数零散客户仅在发班前的2-3天提出预订,并愿意支付较高的运价,这类客户被称为加急客户.为了增加收入,联运经营人可以对普通客户和加急客户进行差别定价,并给加急客户预留出一定数量的箱位.但是,如果预留的箱位数过多,未售出的箱位收入为零;如果预留的箱位数过少,将影响联运经营人的收入.因此,联运经营人需要决策的就是如何将第一阶段箱位分配后的剩余箱位进行再次分配,根据两类零散客户的需求确定各重箱OD节点对上分配给普通客户和加急客户的箱位数量,以使收入最大化.

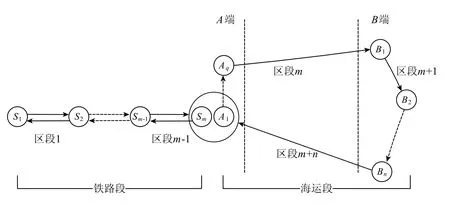
图1 多节点集装箱海铁联运线路描述Fig.1 Description of the multi-node container sea-rail intermodal transport line

3 模型构建

3.1 第一阶段模型

第一阶段的目标是确定各重箱OD节点对上的协议销售箱位数量和各空箱调运OD节点对上的空箱运输量,以使联运经营人期望收入最大化,即有模型(M1)如下:

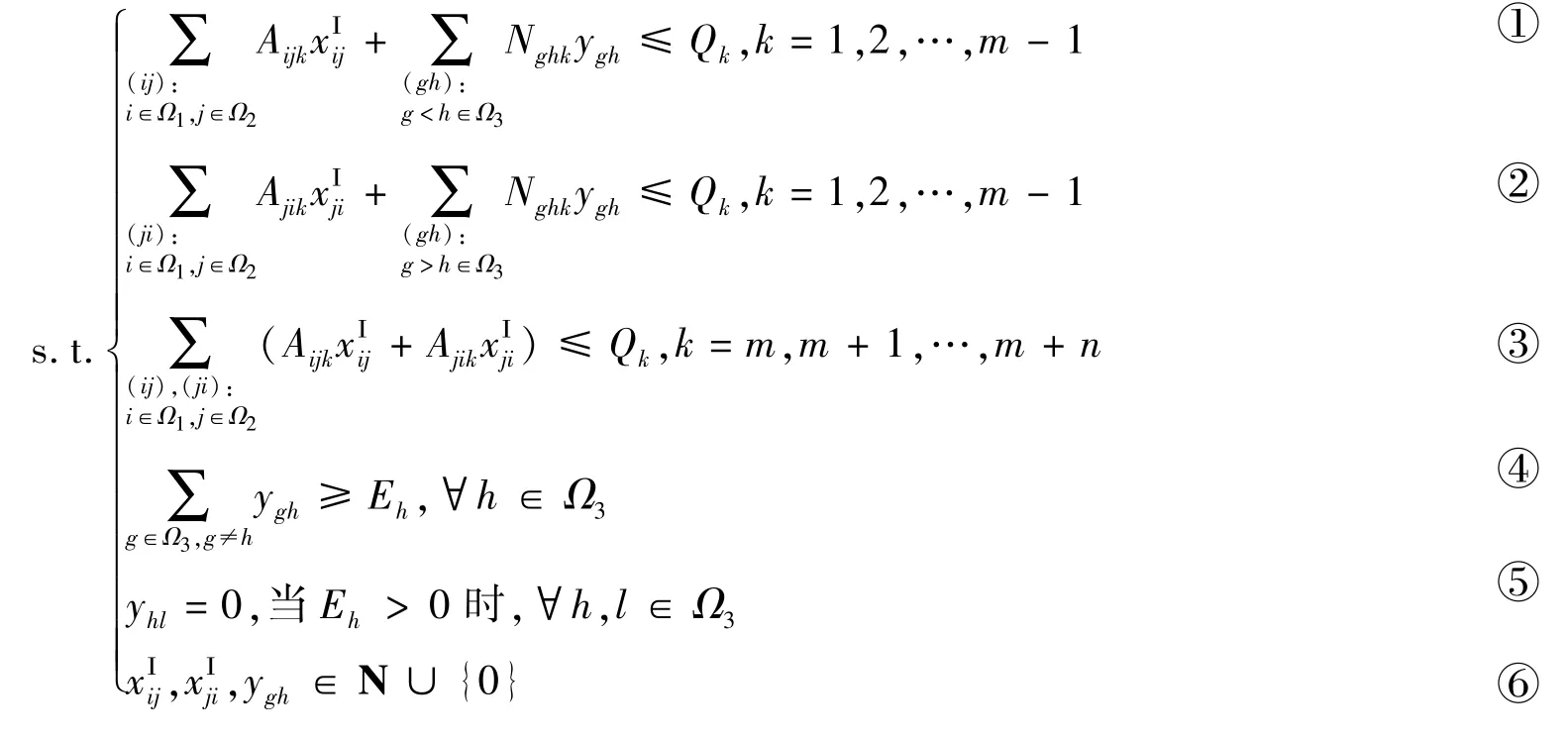
式中

xⅠ

ij、 xⅠji为决策变量,分别表示为去程节点对(ij)上和回程节点对(ji)上分配给合同客户的协议销售箱位数量;

ygh为决策变量,表示节点对(gh)上的空箱运输量;

pⅠ

ij、 pⅠji分别表示去程节点对(ij)上和回程节点对(ji)上合同客户的协议运价;

pgh表示节点对 (gh)上的空箱单位运费率;

DⅠ

ij、DⅠji分别表示去程节点对(ij)上和回程节点对(ji)上合同客户箱位随机需求量;

Eh表示节点h的空箱需求量;

Qk表示联运线路上区段k的总箱位容量, Qk=Q,k=1,2,…,m-1,m,…,m+n.

约束条件①和②分别表示去程和回程所经过铁路各区段的协议销售箱位数量和空箱运输量之和不能超过铁路各区段的最大箱位容量;约束条件③表示经过海运各区段的协议销售箱位数量不能超过海运各区段的最大箱位容量;约束条件④和⑤表示铁路段从各节点运到节点h的空箱数量不小于节点h对空箱的需求量,且需要空箱的节点h不能往其它节点调运空箱;约束条件⑥为决策变量的整数约束.

3.2 第二阶段模型

第二阶段的目标是根据两类零散客户的需求确定各重箱OD节点对上分配给普通客户和加急客户的箱位数量,以使期望收入最大,模型(M2)如下:

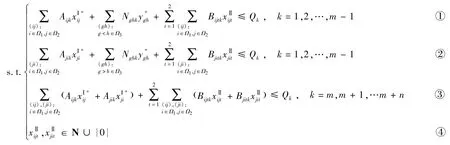
式中

xⅡijt、 xⅡ

jit为决策变量,分别表示为去程节点对(ij)上和回程节点对(ji)上分配给第t类客户的自由销售箱位数量;

t表示自由销售阶段客户分类,t=1代表提前预订的普通客户,t=2代表晚些预订的加急客户;

pⅡijt、 pⅡ

jit分别表示去程节点对(ij)上和回程节点对(ji)上第t类客户的运价;

DⅡijt、DⅡ

jit分别表示去程节点对(ij)上和回程节点对 (ji)上第 t类客户箱位需求的概率累积值;

xⅠij*

、xⅠji*、yg*

h为第一阶段箱位分配模型(M1)的最优解.

约束条件①和②分别表示去程和回程所经过铁路各区段的自由销售箱位数量、协议销售箱位数量和空箱运输量之和不能超过铁路各区段的最大箱位容量;约束条件③表示经过海运各区段的自由销售箱位数量和协议销售箱位数量之和不能超过海运各区段的最大箱位容量;约束条件④为决策变量的整数约束.

4 模型求解

4.1 第一阶段模型转化

模 型 (M1)是 一 个 PMP(Probabilistic Mathematical Programming)模型,对PMP的一种近似求解方法是将PMP中的需求D简单地用其期望值ED代替[7],这种方法被称为DMP(Deterministic Mathematical Programming),再利用LP松弛方法转化为确定性线性规划问题(DLP)进行求解.由于联运经营人需要与合同客户提前签订长期销售合同,则合同客户的箱位需求量基本确定,因此,适合用DLP方法将模型(M1)转化为等价的确定性线性规划模型(M3)如下:

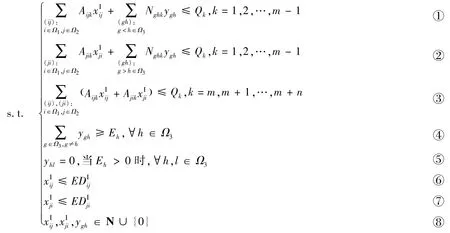
求解模型(M3),即可求得第一阶段的最优箱位分配结果xⅠ

ij*,xⅠ

ji*和yg

*h.

4.2 第二阶段模型转化

模型(M2)也是一个PMP模型,如果同样按照第一阶段的方法转化成DLP模型,则联运经营人不会提供多于期望需求的箱位给高价值的加急客户,而这与实际情况不符,基于需求的随机性,联运经营人往往会为高价值的加急客户预留多于期望需求的箱位.因此,第二阶段采用随机线性规划(SLP)方法求解,从而为运价更高的节点对和客户组合提供更多的箱位.

为了充分估计模型(M2)中需求的随机性,需要表达出需求的概率性.假设每个节点对和客户组合的需求DⅡijt和DⅡjit只能取有限个离散值:{dijt(1)＜ dijt(2)＜ … ＜ dijt(Fijt)}和{djit(1)＜ djit(2)＜ …＜ djit(Fjit)},其中Fijt和Fjit的大小可根据实际情况和希望达到的目的确定,事实上,需求也应该是一个离散性的随机变量.则 Pr(DⅡijt≥ djit(f)) 和Pr(DⅡjit≥djit(f))分别表示随机需求DⅡijt和DⅡjit大于等于某离散值 dijt(f)和 djit(f)的概率.同时,将决策变量xⅡijt和xⅡjit也细分为Fijt和Fjit个部分,即xⅡijt(f), f=1,2,…,Fijt和xⅡjit(f),f=1,2,…,Fjit,分别用于表示需求区间(dijt(f-1),dijt(f)]和(djit(f-1),djit(f)]内为需求DⅡijt和DⅡjit预留的箱位数[8].则模型(M2)可以转化成模型(M4)如下:

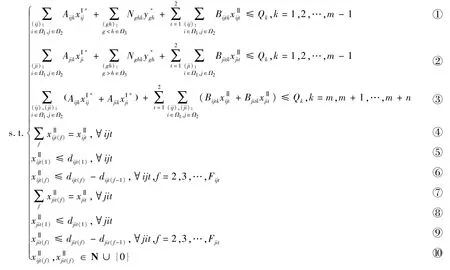
模型(M4)为随机线性规划模型(SLP),求解该模型,即可求得第二阶段的最优箱位分配策略.

5 算例分析

某联运经营人经营一条基于港口A1的多节点集装箱海铁联运线路,铁路段为集装箱办理站S1-S3之间的铁路班列,海运段为A、B两端港口A1-A2-B1-B2之间的顺时针班轮航线,整条线路共有2+3=5个区段,箱位总容量Q=100TEU.各节点对各类客户的重箱运价数据是已知的,假定各节点对各类客户的重箱箱位需求信息已经通过历史数据统计得出,且为服从正态分布的随机变量.表1为各节点对各类客户的运价信息和需求分布情况.若空箱需求仅发生在铁路段节点S1和S2,节点S1的空箱需求量为6 TEU,节点S2的空箱需求量为2 TEU,则可能的空箱调运节点对只有S3-S1和S3-S2,空箱调运成本分别为 600元/TEU和240元/TEU.表2为第二阶段各节点对各类客户的需求离散取值及其概率.

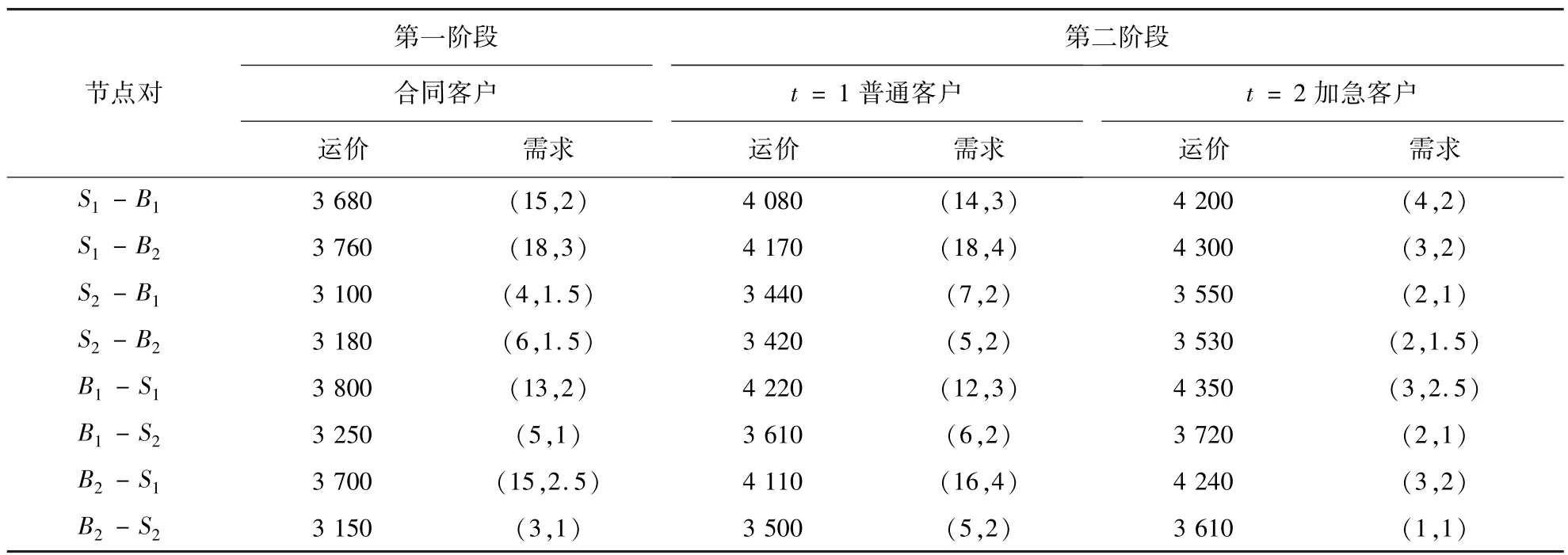
表1 运价信息和需求分布情况表Table 1 The information of price and demand distribution

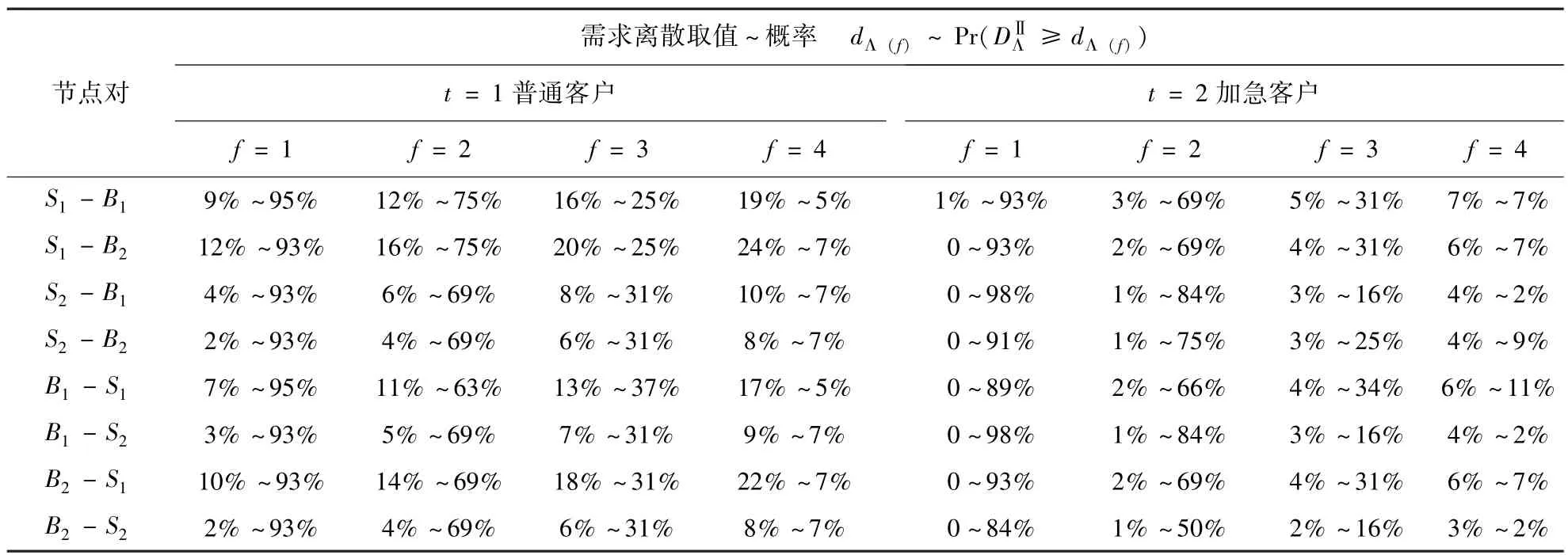
表2 第二阶段需求离散取值及概率表Table 2 Discrete values and probabilities of demand in the second stage

根据表1和表2中数据,利用Lingo软件包对模型(M3)和模型(M4)进行整数规划求解,可以得到两阶段客户细分策略的箱位分配方案,其中,空箱调运方案为S3-S1节点对调运6TEU,S3-S2节点对调运2TEU,空箱调运总成本为4 080元.同时,根据同样的数据,利用 Lingo软件包对模型(M3)进行同样的求解,而对模型(M4)仅取t= 1(不考虑t=2)进行求解,可以得到两阶段一般策略的箱位分配方案,其中,空箱调运方案与前者相同.两种策略的计算结果如表3所示.

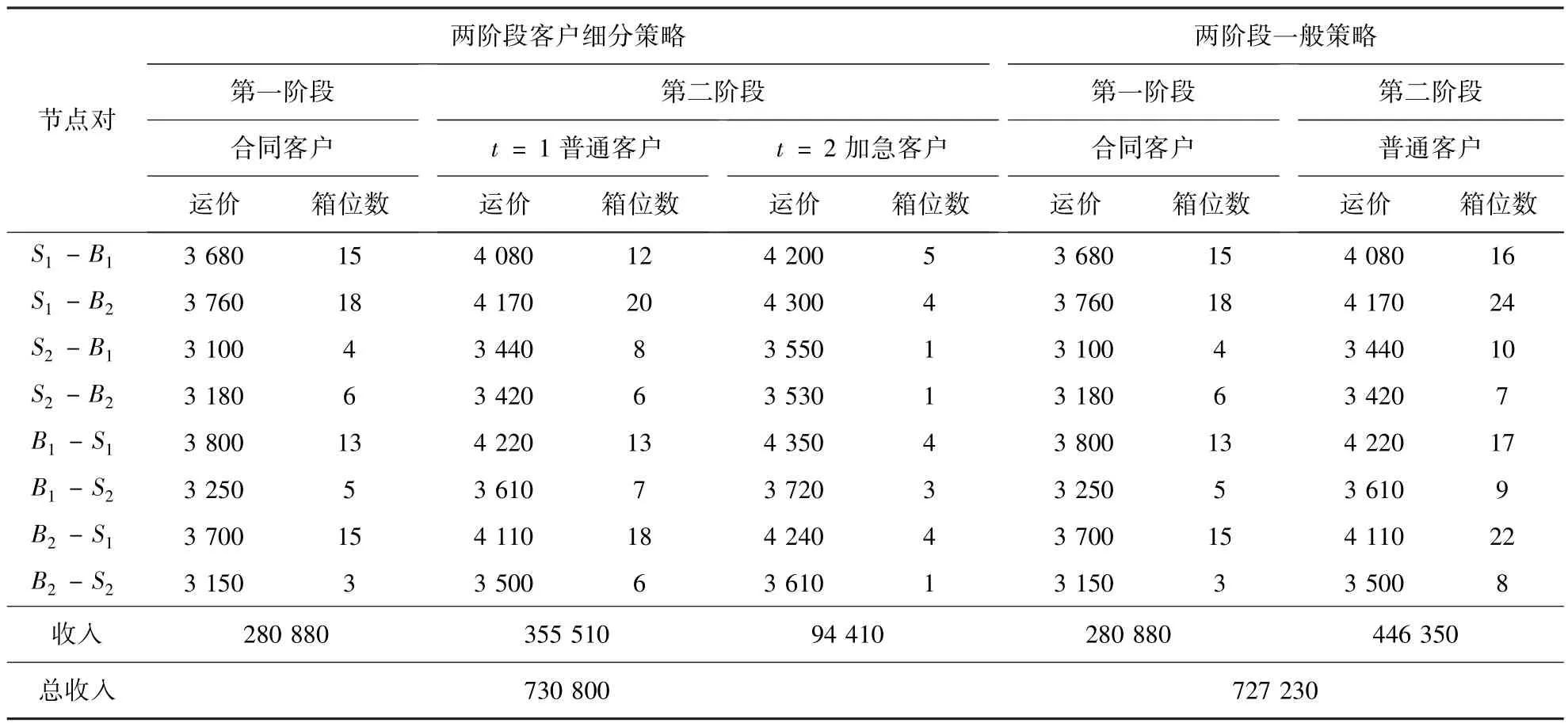
表3 算例计算结果汇总表Table 3 Summary of example results

由表3可以看出,第一阶段箱位分配数等于各节点对合同客户的需求期望,而第二阶段由于考虑了需求的随机性,采用SLP方法为运价更高的节点对和客户组合分配了更多的箱位.若联运经营人采用两阶段客户细分策略,即第一阶段为合同客户,并且将第二阶段零散客户进一步细分为普通客户和加急客户,其总收入为730 800元;若采用两阶段一般策略,即第一阶段为合同客户,而第二阶段不对零散客户进一步细分,仅考虑零散客户都为普通客户,其总收入为727 230元,低于前者3 570元.由此可见,联运经营人采用两阶段客户细分的箱位分配策略,可以在不确定环境下满足货主需求的同时提高收入,该模型和算法更为适用和有效.

6 研究结论

本文基于收益管理的思想,以集装箱海铁联运经营人对市场需求的细分和差异定价策略为切入点,分协议销售和自由销售两个阶段建立了多节点集装箱海铁联运箱位分配优化模型.第一阶段模型解决了在既定协议销售运价下各节点对上合同客户的箱位分配问题,并针对合同客户需求的相对确定性特征用DLP方法进行求解;第二阶段模型将零散客户进一步细分为普通客户和加急客户,解决了在差异化的自由销售运价下各节点对上普通客户和加急客户的箱位分配问题,并考虑需求的随机性特征用SLP方法进行求解.通过算例,验证了模型和算法的可操作性和有效性.

本文研究的仅仅是一条联运线路的箱位分配问题,今后将结合实际情况进一步扩展和完善,如考虑多条联运线路间的转运、集装箱种类的不同、退订和超订的处理等.

[1]刘迪,杨华龙.单起讫点间集装箱海铁联运动态定价模型[J].交通运输系统工程与信息,2012,12 (4):122-127.[LIU D,YANG H L.Dynamic pricing model of container sea-rail lntermodal transport on single OD line[J]. JournalofTransportation Systems Engineering and Information Technology,2012,12 (4):122-127.]

[2]Ting S C,Tzeng G H.Fuzzy multi-objective programming approach toallocating containership slotsforliner shipping revenue management[C]. The 16th International Conference on MCDM.Semmering:[s. n],2002:1-16.

[3]Feng C M,Chang C H.Optimal slot allocation with empty container reposition problem for Asia ocean carriers[J].International Journal of Shipping and Transport Logistics,2010,2(2):22-43.

[4]Sebastian Zurheide,Kathrin Fischer.A simulation study for evaluating a slot allocation model for a liner shipping network[C].Proceedings of the Second International Conference on Computational Logistics, Springer-Verlag,Berlin,Heidelberg,2011:354-369.

[5]卜祥智,赵泉午,黄庆,等.考虑空箱调运的集装箱海运收益管理能力分配优化模型[J].中国管理科学,2005,13(1):71-75.[BU X Z,ZHAO Q W, HUANG Q,et al.Optimal capacity allocation model of ocean shipping container revenue management considering empty container transportation[J].Chinese JournalofManagementScience,2005,13(1): 71-75.]

[6]卜祥智,陈荣秋,赵泉午.考虑长期合同运力的班轮收益管理运输路径优化模型[J].中国管理科学, 2007,15(6):39-45.[BU X Z,CHEN R Q,ZHAO Q W.An optimization model of routing problem with long-term contract for liner revenue management[J]. Chinese Journal of Management Science,2007,15(6): 39-45.]

[7]Sanne V de Boer,Richard Freling,Nanda Piersma. Mathematical programming for network revenue managementrevisited[J]. European Journal of Operational Research,2002,(137):72-92.

[8]周晶,杨慧.收益管理方法与应用[M].北京:科学出版社,2009.[ZHOU J,YANG H.Revenue management methods and applications[M].Beijing: Science Press,2009.]

Slot Allocation Optimization Model for Multi-node Container Sea-Rail Intermodal Transport

LIU Di1,2,YANG Hua-long1,ZHANG Yan1
(1.Transportation Management College,Dalian Maritime University,Dalian 116026,Liaoning,China; 2.School of Traffic and Transportation Engineering,Dalian Jiaotong University,Dalian 116028,Liaoning,China)

Slot allocation optimization under uncertain demands has significant impacts on the efficiency and benefit for a multimodal transport operator(MTO).Based on revenue management theory and features of container sea-rail intermodal transport,this paper establishes a two-stage slot allocation optimization model on the multi-node container sea-rail intermodal line,which takes into account the different demands of contract,general and urgent customers.The first stage is proposed by considering slot allocation for contract customers in contract market,and the second stage is proposed by considering slot allocation for general and urgent customers in free market.Because of the demand relative certainty in the first stage and the demand uncertainty characteristic in the second stage,the method of DLP and SLP are used to transform and solve the models respectively.The results show that the models and algorithms are feasible and effective.

U169.6 F50

A

U169.6 F50

A

1009-6744(2013)02-0164-08

2012-11-26

2013-01-03录用日期:2013-01-16

国家自然科学基金项目(70972008,71202108);大连市科技计划项目(20120275);中央高校基本科研业务费资助暨大连海事大学优秀科技创新团队培育计划资助项目(2011ZD027).

刘迪(1982-),女,沈阳市人,博士生,讲师.

*通讯作者:hlyang@dlmu.edu.cn

Key words:integrated transportation;slot allocation;revenue management;container;sea-rail intermodal transport;optimization model