基于免疫粒子群算法的PID参数整定与自适应
邓 丽 蒋 婧 费敏锐
(上海大学机电工程与自动化学院,上海 200072)
0 引言
在工业过程控制中,PID控制具有步骤简单、鲁棒性强等优点,被广泛应用于各个领域。据统计,PID控制策略在实际控制系统中所占的比例超过90%,而针对PID控制器的参数整定和自适应一直是最重要的问题所在。Ziegler和Nichols在1942年设计出了Z-N整定公式,这是最早的PID参数整定方法,至今它还普遍应用在各种工业控制场合。1953年,Cohen和Coon继承和发展了Z-N公式,设计了一种考虑被控过程时滞大小的 Cohen-Coon 整定公式[1]。
传统PID控制器的结构普遍存在积分饱和、超调量大,以及由于微分作用对高频干扰敏感而导致的系统失稳等缺点。此外,传统PID控制的另一个问题是不能使目标值跟踪特性和干扰抑制特性同时最优,而任何一个工业过程对扰动抑制品质和跟踪给定品质都是有要求的。如今,将自适应控制、最优控制、预测控制、鲁棒控制和智能控制策略引入传统PID控制,逐步发展成为一种新型PID控制[2]。
文献[3]尝试将粒子群(particle swarm optimization,PSO)算法引入PID控制。PSO算法是一种从仿生学进化而来的优化算法,计算过程简捷,优化效果好,但是PSO算法具有容易陷入早熟等缺点。为了解决这个问题,本文引入免疫算法。免疫算法具有免疫和遗传等特点,能够帮助防止粒子群陷入早熟;同时,将PSO算法和免疫算法相结合,也避免了免疫算法计算过程繁复冗长的缺点。
1 PID控制基本原理
PID控制是基于对变量“过去”、“现在”和“未来”信息估计的交叉控制算法。系统主要由被控对象和PID控制器两部分组成,如图1所示。

图1 PID控制系统图Fig.1 PID control system
常规的PID一般为线性控制器,实际输出值和给定值会存在一个偏差,将偏差按比例、积分和微分的线性组合来构成控制量,从而对被控对象进行控制。这个过程称为PID控制器。
PID控制器的参数整定与自适应是指根据系统模型和各种性能指标,将控制器确定为PID形式的情况下,采用各种方法调整PID控制器的参数,使由控制对象、控制器、执行元件、反馈元件等组成的控制回路的动态特性与静态特性能满足期望的要求,达到理想的控制目标。
2 ISPSO算法介绍
2.1 粒子群算法
近年来,粒子群算法(PSO)作为一种新生的随机进化计算方法,由于具有简捷通用、适合并行处理、对目标函数和约束条件要求低等特点而得到广泛应用。但由于PSO算法是根据全体粒子和自身的搜索经验向着最优解的方向“飞行”,在进化过程中粒子群多样性会下降,因此当算法收敛到一定精度时,无法继续优化,容易陷入局部最优,造成所能达到的精度较差[4]。粒子迭代更新公式如式(1)所示。
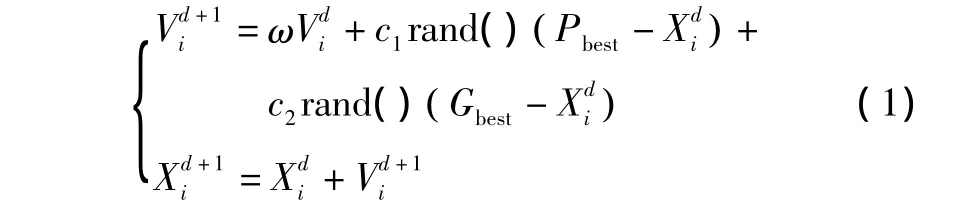
式中:d为迭代次数;ω为惯性权重;c1、c2为学习因子;rand()为均匀分布在(0,1)之间的随机数。
2.2 免疫算法
免疫算法也是科学家从人类仿生学上得到启发而设计的一种算法[5]。在生命科学领域,人们已经对遗传与免疫等自然现象进行了广泛而深入的研究。从遗传算法演变而来的免疫算法几乎与遗传算法一样,只是多使用了一个免疫函数,它是遗传算法的变体,不用杂交,而是采用注入疫苗的方法。
2.3 ISPSO算法的基本原理
基于免疫选择的粒子群算法(immunity selectionparticle swarm optimization,ISPSO)将免疫系统的免疫信息处理机制引入PSO算法中,将待求解问题视为抗原,每一个抗体代表问题的一个解,同时每个抗体也即是粒子群中的一个粒子。抗原与抗体的亲和力由PSO算法中的适应度来衡量,反映了对目标函数以及约束条件的满足程度;抗体之间的亲和力则反映了粒子之间的差异,即种群的多样性。
与标准PSO算法相比,免疫粒子群算法主要由以下3个部分组成。
①基本的PSO算法,可独立运行,用于控制整个算法的优化迭代过程;
②免疫记忆与自我调节功能的实现,用于保证种群的多样性;
③疫苗接种的实现,用于提高算法的收敛性能[6]。
2.4 ISPSO 算法流程
基于免疫选择的粒子群(ISPSO)算法流程如下。
①初始化粒子群:在允许范围内随机产生N个粒子的位置及其速度,计算适应值,得到初始化群体的个体极值和全局极值。
②产生免疫疫苗:即将全局最优粒子作为免疫“疫苗”。
③更新粒子的位置和速度:按照式(1)对每个粒子的速度和位置进行更新。
④群体的更新:将更新后粒子的适应值与更新前粒子的适应值进行比较,如果适应值增加,则粒子的位置才进行更新,否则保留原来粒子的位置。
⑤随机产生新的粒子:为了增加群体的多样性,在每次迭代过程中都随机产生M个新粒子,并计算适应值。
⑥概率选择N个粒子形成新的群体:从(N+M)个粒子形成的群体中,按照概率选择N个粒子形成新的群体[7]。
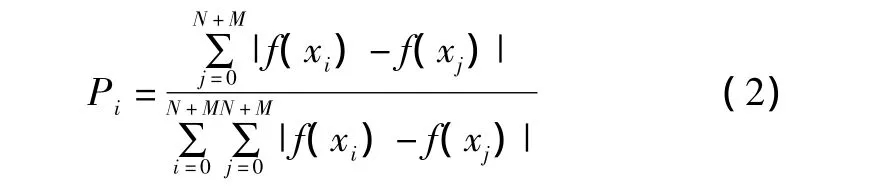
⑦免疫接种和免疫选择:用步骤②产生的免疫“疫苗”对群体中的R个粒子进行疫苗接种,计算接种疫苗后的粒子适应度值,并根据适应度值进行免疫选择。如果适应值减小,则保留该粒子,否则取消疫苗。这样就形成了新一代群体。
⑧更新群体的个体极值和全局极值:根据新一代群体的适应值,更新群体的个体极值和全局极值。
⑨判断是否满足约束条件:如果迭代次数大于最大迭代次数,则结束循环、输出结果;否则转到步骤②。
3 PID控制器参数设计
采用基于免疫选择的粒子群优化算法整定PID控制器参数,必须建立综合评价各项性能指标的适应度函数,用于评价粒子的优劣,并作为个体最优粒子和全局最优粒子更新的依据,使得初始解逐步向最优解进化。
通常一组好的PID控制参数Kp、Ki和Kd会产生良好的阶跃响应曲线和最小时域性能指标。时域性能指标主要包括:调节时间ts、上升时间tr、最大超调量Mp和稳态误差ess。本文定义适应度函数为ITAE[8],如式(3)所示。

4 仿真试验
选用a、b、c三个系统,其传递函数如式(4)~式(6)所示[9-12]。利用基于免疫选择的粒子群优化算法进行迭代计算,并与简单的PSO优化算法进行比较,运用Matlab软件进行仿真。程序中算法参数选取如下:粒子数N=40;学习因子c1=c2=2.0;ω在0.4~0.9之间取值,并且随着迭代次数的增加而线性减小;迭代次数最大为100。
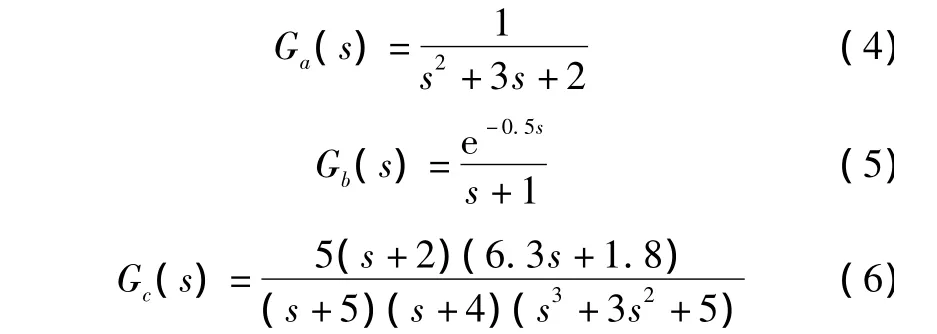
三个系统的Matlab仿真结果如图2所示。三个系统均经过PID控制器调整后,再经过反馈最终达到稳定状态。由图2可知,系统a在PID控制器作用下比较容易稳定,其次是b系统;阶数越高,越难用算法计算出较好的控制器参数;本文的算法效果较单纯的PSO算法好。
三个系统的计算结果和动态特性如表1所示[13-15]。
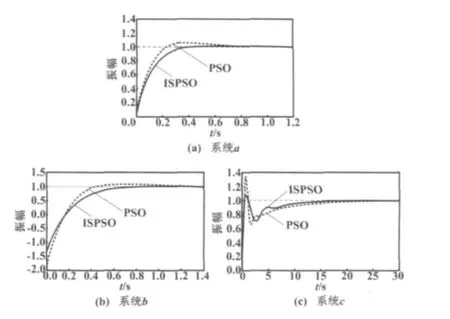
图2 Matlab仿真结果Fig.2 Results of Matlab simulation

表1 三个系统的计算结果和动态特性Tab.1 Calculated results and dynamic characteristics of 3 systems
由表1可以看出,在采用本文算法计算出的控制器的控制下,系统的超调量和调节时间明显减少。另外,由表1中系统c的PSO的Kp数据可以看出,经计算,粒子群已经飞向边界并且陷入早熟[16-19]。因此,综合上述分析可知本文提出的算法效果更佳。
5 结束语
针对常规PID控制方法的不足,本文提出采用基于免疫选择的粒子群优化算法来自整定PID控制器参数。基于免疫选择的粒子群优化算法不仅保持了PSO算法的快速跟踪效果和免疫算法的平稳性,同时可有效地避免PSO算法和免疫算法陷入局部解。在加入扰动因素之后,免疫粒子群优化算法的鲁棒性明显优于PSO算法和免疫算法。Matlab仿真结果表明,该算法能够减小系统调节时间和超调量,系统动态性能得到较大改善,对于大惯性、非线性、时变控制系统具有良好的控制性能。
[1]王蕾,宋文忠.PID 控制[J].自动化仪表,2004,25(4):1 -5.
[2]杨智,陈志堂,范正平,等.基于改进粒子群优化算法的PID控制器整定[J].控制理论与应用,2010,27(10):1345 -1352.
[3]张家骏.基于粒子群算法的PID控制器参数优化研究[J].计算机仿真,2010(10):191-193.
[4]冯骏,薛云灿,江金龙.一种新的改进粒子群算法研究[J].河海大学常州分校学报,2006,20(1):10 -13.
[5]王磊,潘进,焦李成.免疫算法[J].电子学报,2000(7):74 -78.
[6]吴静敏,左洪福,陈勇.基于免疫粒子群算法的组合预测方法[J].系统工程理论方法应用,2006,15(3):229 -233.
[7]陈曦,蒋加伏.免疫粒子群优化算法求解旅行商问题[J].计算机与数字工程,2006,34(6):10 -12.
[8]李自强,薛美盛.用于PID参数自整定的性能指标仿真研究[J].自动化与仪表,2009(2):30-33.
[9]张蛟,李银伢,盛安冬.一阶参数不确定滞后过程的鲁棒PID控制器设计[J].计算机仿真,2006(12):174-178.
[10]Kennedy J,Eberhart R.Particle swarm optimization[C]//Proceedings of International Conference on Neural Networks,Perth,Australia:IEEE,1995:1942-1948.
[11]Gaing Z L.A particle swarm optimization approach for optimum design of PID controller in AVR system[J].IEEE Transactions on Energy Conversion,2004,9(2):384 -391.
[12]Shi Y,Eberhart R.A modified particle swarm optimizer[C]//Proceedings of International Conference on Evolutionary Computation,Anchorage,Alaska:IEEE,1998:69 -73.
[13]Cohen G H,Coon G A.Theoretical consideration of retarded control[J].Transactions of ASME,1953,75(4):827 -834.
[14]邓伟林,胡桂武.粒子群算法研究与展望[J].现代计算机:专业版,2006(11):12-15.
[15]王芳.粒子群算法的研究[D].重庆:西南大学,2006.
[16]卢泽生.控制理论及其应用[M].哈尔滨:哈尔滨工业大学出版社,2005.
[17]欧阳黎明.MATLAB控制系统设计[M].北京:国防工业出版社,2001.
[18]薛定宇.控制系统仿真与计算机辅助设计[M].北京:机械工业出版社,2005.
[19]黄忠霖.控制系统MATLAB计算及仿真[M].北京:国防工业出版社,2001.

