基于Z-O编码的两层WSNs隐私保护最值查询处理协议
戴 华 秦小麟 刘 亮 季一木 付 雄 孙 研
①(南京邮电大学计算机学院 南京 210003)
②(南京航空航天大学计算机科学与技术学院 南京 210016)
1 引言
目前,无线传感器网络(Wireless Sensor Networks, WSNs)已被广泛用于诸如环境监测、医疗卫生、智能交通、国防军事等各种重要领域。而两层WSNs(Two-tiered Wireless Sensor Networks)[1]是一种以存储节点(storage nodes)为中间层的无线传感器网络,其中存储节点为计算、存储和能量资源充足的传感器节点,其上层为Sink节点,下层为资源受限的一般感知节点(sensor nodes),存储节点与查询区域内其负责管理的所有感知节点构成查询单元(query cells)。由于两层WSNs的拓扑结构的简单性和中间层存储节点的资源充裕性,使得两层WSNs具有链路质量稳定、路由结构简单、查询高效和负载均衡等优点[1,2]。然而,由于存储节点所处位置的重要性,不仅存储着大量感知数据,同时还负责执行上层的查询请求,这就使得存储节点往往成为各种攻击的主要目标。研究和解决两层WSNs中的安全和隐私保护问题,对于促进无线传感器网络技术的大规模应用具有重要的现实意义。
在面向两层 WSNs的隐私保护查询处理技术中,现有研究重点关注范围(range)查询中的隐私保护技术[3-6],对于最值(MAX/MIN)查询处理的研究相对较少,目前仅有文献[7]提出了初步的解决方法,该方法利用前缀编码验证(Prefix Membership Verification, PMV)机制[3],给出了一种无需感知数据明文参与的数值线性关系比较方法,进而实现满足隐私保护要求的最值查询处理方法(记为 PMVMQP)。然而,该方法采用的前缀编码机制产生的数据量较大,并且每一个感知节点都需要加密感知数据并传送密文数据,导致该查询处理过程需要较大的能耗开销。此外,文献[8]提出了工作于多跳WSN中基于k-隐藏的最值聚集查询方法,但该方法只能查询最值数据,无法查询产生最值数据的传感器节点位置信息。
本文以两层WSNs为研究背景,重点讨论面向两层WSNs的隐私保护最值查询处理技术,即在实现最值查询处理的过程中,确保感知数据和最值查询结果不泄露,以保证感知数据和最值查询结果的隐私安全性。基于此,本文提出了基于Z-O编码的两层WSNs隐私保护最值查询处理协议。通过引入安全多方计算中的Z-O编码技术[9],并结合Hash消息身份验证编码机制(Hashed Message Authentication Code, HMAC)[10],对感知数据进行HMAC数值化Z-O编码处理,然后利用Z-O编码集合的数值比较特性,实现在无需感知数据明文参与下的数值线性关系比较,并利用加密技术确保感知数据传输过程中的隐私安全性。在上述隐私保护措施的基础上,给出基于Z-O编码的隐私保护最值查询处理协议(Z-O Encoding based Privacy Preserving Max/Min query process protocol, ZOPPM),并对该协议进行能耗和隐私安全性分析。实验结果表明,ZOPPM协议的能耗优于现有的方法。
2 问题描述
在两层WSNs的查询处理过程中,如果不对感知数据进行处理,直接以明文形式参与查询,当存储节点被俘获,该节点将能够获取所有存储在该节点,以及利用该节点进行转发的感知数据,并且还能够获取由该节点计算出的部分查询结果。与此同时,由于传感器节点数据通信的广播特性,在感知节点发送数据的一跳(hop)范围内,其他任何节点(存储节点或感知节点)都可以收到数据。因此,需要在查询处理过程增加隐私保护措施,以确保感知数据和查询结果的隐私安全性。
最值查询即为获取查询区域内的感知节点采集到的数据最大值(MAX)或最小值(MIN)及其位置信息的计算过程。最值的计算必然需要比较数值的线性关系,所以解决最值查询问题,首先需要解决如何在不泄露隐私的情况下比较两个感知节点的数据大小问题,该问题类似于安全多方计算研究中一个经典问题——百万富翁问题[11]。
与文献[3,7,8]类似,本文也假设查询发起节点Sink可信,并假设两层WSNs中的存储节点和感知节点都有试图窥探其他节点数据的企图,但仍然能够遵循查询处理协议进行最值计算,即符合honestbut-curious威胁模型[12]。此外,假设两层WSNs的拓扑结构稳定,感知节点采集感知数据,存储节点只负责计算和存储;存储节点拥有其负责的感知节点的位置和ID信息,而感知节点也拥有对应存储节点的位置和ID信息,Sink则拥有所有感知节点和存储节点的位置和ID信息。
在上述假设条件下,实现具有隐私保护能力的最值查询,就必须确保查询处理过程满足:(1)对于网络中的任一感知节点的感知数据,只有该感知节点本身和Sink可以读取其明文数值;(2)对于最终的最值查询结果(包含数值和位置信息),只有Sink拥有,而其他任何节点都无法获得。此外,存储节点的能量资源充足,而感知节点的能耗有限,因此,降低感知节点的能耗开销也是两层WSNs查询处理技术研究的一个重要目标。
3 基于Z-O编码的数值比较方法
本节我们将在文献[9]的基础上,给出基于 Z-O编码数值比较方法。
定义1Z-O编码(Zero-One encoding):设包含w个二进制位的数值x=b1b2…bw-1bw(bi∈{0,1}且1≤i≤w),对x进行Z-O编码,得到的Z编码集合Z(x)和O编码集合O(x)为
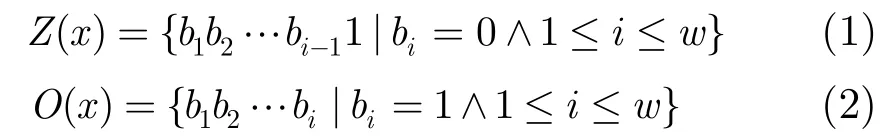
其中b1b2…bw-1bw是数值x的二进制编码表示,b1为最高位,bw为最低位。
性质1设数值x为包含w个二进制位,则Z(x)和O(x)满足如下性质:
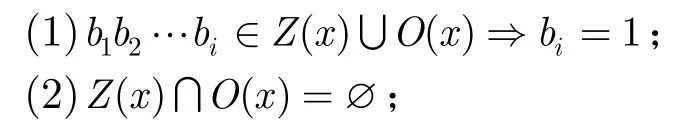
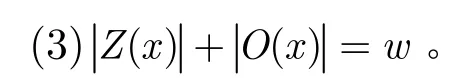
由定义1容易得到性质1成立(证略)。
性质2若已知数值x的Z编码集合或O编码集合,不难反向逆推出数值x。
由定义1中的Z-O编码方法及性质1的内容,易得性质2成立。例如,若已知包含4个二进制位的数值x的Z编码集合Z(x)={1},则x必定为0111。
定理1对于都包含w个二进制位的数值x和y,当且仅当O(x)与Z(y)不相交时,x>y成立;当且仅当O(x)与Z(y)存在非空交集时,x≤y成立,即有式(3)和式(4)成立。
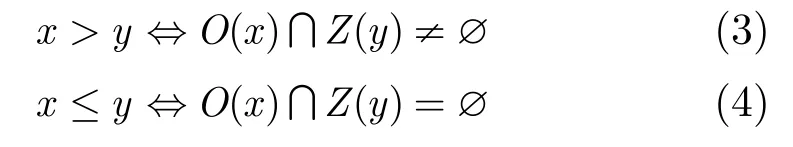
定理1的证明详见文献[9]。由定理1可知,数值x和y的大小比较问题,可以转化为判断Z编码集合与O编码集合是否存在交集的问题。显然,如果将Z编码集合和O编码集合中的元素都转换为具体数值,则可以简化集合相交的计算过程。为了保持Z-O编码的数值比较特性,对于Z-O编码的数值化方法必须满足定义2要求。
定义2若将任意Z-O编码二进制序列p的数值化方法记为N,得到的数值化Z-O编码记为N(p),则对于任意两个Z-O编码二进制序列p1和p2,该数值化方法应满足:
(1)p1=p2⇔N(p1)=N(p2);
(2)p1≠p2⇔N(p1)≠N(p2)。
显然,针对Z-O编码的数值化方法并不唯一。本文给出一种简单的数值化方法Ns:对于数值x的任一Z-O编码序列p=b1b2…bi,则p数值化后得到Ns(p)=1b1b2…bi,即在二进制序列b1b2…bi的最高位之前增加“1”。容易证明,该数值化方法Ns符合定义2要求。
4 基于 Z-O编码的隐私保护最值查询处理方法
4.1 基本思想
在介绍本文研究工作的基本思想之前,我们首先给出查询单元的形式化定义。
定义3查询单元(query cell):存储节点S与其在查询区域内的负责的所有感知节点ℕ={s1,s2,…,sn}(ℕ≠∅)构成一个查询单元,记为 qcS=(S,ℕ)。
根据定义3的要求,任一查询单元只包含一个存储节点,且至少包含一个感知节点。此外,由于存储节点拥有其负责的感知节点的位置信息,因此,该存储节点能够计算出其所在的查询单元或者不构成查询单元。为了方便讨论,我们假设任一感知节点最多只存在于一个查询单元中。
本文的面向隐私保护的最值查询处理方法的基本思想主要包含如下两个阶段:
(1)查询指令广播阶段首先 Sink将查询指令MQ={t,qa, MAX/MIN}(表示查询满足时刻t和区域qa要求的最大/最小的感知数据)广播到所有存储节点;存储节点S收到MQ后,判断是否构成查询单元qcS,若构成,则S再将MQ转发至qcS内的所有感知节点,否则不参与查询处理。
(2)最值查询处理阶段在每一个查询单元 qcS=(S,{s1,s2,…,sn})中,si发送其感知数据的 HMAC数值化Z-O编码数据给S;根据收到的qcS内所有感知节点发来的编码数据,S计算出qcS内产生最值的节点sj,并通知sj发送感知数据;当sj收到S的数据请求,sj立即加密其感知数据,并将密文发回给S;而S收到密文数据后,构造qcS的局部查询结果lqr(local query result)并发送给Sink;最后,Sink根据各个查询单元发送的lqr,计算出最终的全局查询结果gqr(global query result),并返回给用户。
在查询处理阶段,为了确保感知数据和查询结果的隐私安全性,我们采取如下隐私保护措施:
(1)当si需要发送其感知数据di给S时,首先利用对称加密方法(如RC4, RC5, IDEA等)对di进行加密处理,生成密钥为ki的加密数据(di)ki,si仅与Sink共享ki,然后将(di)ki发送给S;
(2)为了消除Z-O编码的可逆推性,在编码过程中增加HMAC处理。HMAC机制的单向性和抗冲突性,将使得感知数据di经过 HMAC数值化处理后,即可得到不可逆的 HMAC数据集合 HMACg(Ns(Z(di)))和HMACg(Ns(O(di))),其中g为所有感知节点共享的HMAC密钥。
4.2 具有隐私保护能力的最值查询处理协议ZOPPM
下面,我们以最大值查询处理为例,给出两层WSN中基于Z-O编码的隐私保护最值查询处理协议。我们分别从查询单元和Sink节点这两个方面,讨论ZOPPM协议的工作过程。
设lqrHMAC为存放HMAC数值化Z-O编码数据的变量,lqrnode为存储感知节点ID的变量,lqr(S)={id, cv}为存储节点S所在查询单元的局部查询结果变量,gqr={id, pv}为存储全局查询结果的变量,其中id为感知节点ID, cv为密文数据,pv为明文数据,MD为密文传送指令。则具体协议内容如表1所示。
由ZOPPM协议内容可知,两层WSN中的最值查询处理由Sink,存储节点和感知节点共同协作完成。在查询处理过程中,加密机制确保了感知数据在传输过程中的安全性,而HMAC机制的应用,使得恶意节点无法利用Z-O编码反向逆推原始感知数据,进而保证了两层 WSN中感知节点的隐私安全性。

表1 基于Z-O编码的隐私保护最值查询处理协议
4.3 协议分析
4.3.1隐私安全性分析我们主要从感知数据和查询结果角度,分析ZOPPM协议的隐私安全性。
(1)感知数据的隐私安全性 在本文基于可信Sink节点的前提下,对于任意感知节点si及其本地感知数据di而言,仅当查询处理方法能够确保其它感知节点和存储节点都无法获取di时,di才是隐私安全的。而我们提出的ZOPPM协议能够保证感知数据的隐私安全性:
首先,在最值查询处理过程中,si在传输di时,需首先利用对称加密方法对di进行加密处理(密钥仅与 Sink共享)。因此,在无密钥的情况下获取di的复杂度与破解加密算法相同,从而确保任意传输路径中的其它感知节点或存储节点都无法获取其明文数据。
其次,我们利用HMAC机制,对感知节点发送给存储节点的数值化Z-O编码集合进行HMAC处理,使得存储节点在无需感知数据明文参与的情况下,即可实现各感知数据的大小比较;同时也使得其它能够获得HMAC数据的节点,都无法反向逆推其对应的感知数据。
(2)最值查询结果的隐私安全性 最值查询结果由最值数据和最值位置这两方面组成。其中,最值数据同样也是由某个感知节点产生的感知数据,由本节(1)中的讨论可知,最值数据的隐私安全性同样能够保证。这里,我们重点分析ZOPPM协议对于最值位置的隐私保护能力。
对于最值查询处理而言,产生最值的感知节点的位置信息同样也需要保护。假设网络中共有k个构成查询单元的存储节点,则这些存储节点将产生k个局部查询结果(包含局部最值的位置信息),而最终的全局查询结果在其中产生,并由Sink负责计算。可见,全局查询结果的位置信息,隐藏在k个局部查询结果中,任一存储节点获得全局查询结果位置的概率仅为1/k。因此,ZOPPM协议对最值位置的隐私保护满足k-隐藏(k-indistinguishable)特性,其中k为网络中构成查询单元的存储节点的数量。
由上述隐私安全性分析可知,ZOPPM 协议具有较好的隐私安全保护能力,不仅能够确保感知数据的隐私安全,同样能够保护最值查询结果的隐私安全性。
4.3.2能耗分析在两层WSN中,由于存储节点具有充足的存储空间和能量储备,因此,整个网络的生命周期主要受感知节点的能耗影响。为了尽可能提高网络的生命周期,我们以降低感知节点的能耗为主要目标。
在本文的最值查询处理方法中,感知节点的总能耗Etotal的计算公式如式⑸所示,

其中Ecomm表示感知节点接收和发送数据所带来的通信能耗,Ecomp表示感知节点进行加密和 HMAC计算所带来的计算能耗。

由ZOPPM协议可知:每个感知节点收到存储节点发送的MQ和MD各一次;并且,每个包含w位的感知数据对应的 Z-O编码集合将包含w个HMAC数据;此外,每个查询单元中将有一个感知节点对本地感知数据进行加密,并发送密文数据给存储节点。因此,通信能耗Ecomm为
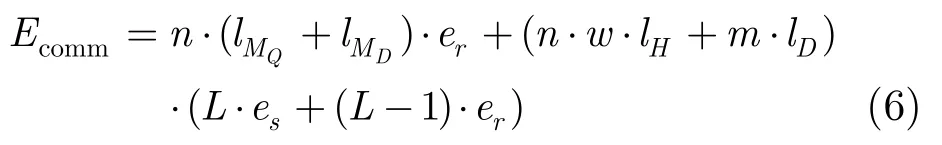
此外,计算能耗Ecomp为感知节点进行加密和HMAC计算的能耗之和,则有
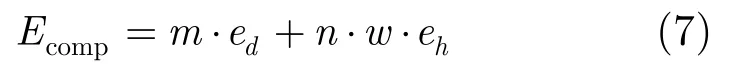
由式(6),式(7)进而可以得到感知节点的总能耗Etotal的最终计算公式为
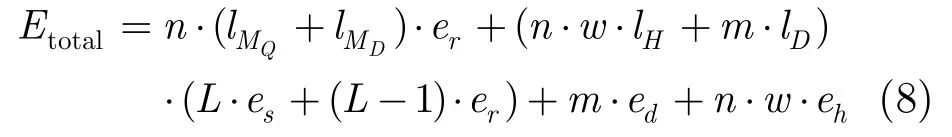
而文献[7]提出的基于前缀成员验证的两层WSN最值查询处理方法(PMV-MQP),其基本思想为:对于任一感知节点si的感知数据di∈[dbot,dtop](dbot和dtop分别为感知数据的已知下界和上界),si针对di和[di,dtop]分别计算相应的HMAC数值化前缀编码集合F和S,若di包含w个二进制位,则F和S满足|F|=w+1和 1≤|S|≤2w-2,si需要计算的HMAC数据总量为|F|+|S|∈[w+2, 3w-1];同时,si还对di进行加密处理,然后将 HMAC数据和加密数据都发送给存储节点,以进行后续的最值查询处理。可见,PMV-MQP总能耗在理论上存在上限和下限;并且,与本文提出的ZOPPM相比,在同等情况下PMV-MQP将消耗更多的通信和计算能耗。我们将在第5节对ZOPPM和PMV-MQP的能耗问题作进一步的实验对比分析。
5 实验分析
为了对协议的性能进行比较和分析,本文在文献[13]的仿真器上实现了ZOPPM与PMV-MQP。通过模拟仿真,我们对这两种方法的能耗进行对比试验,其中,PMV-MQP(top)和 PMV-MQP(bot)分别表示PMV-MQP的能耗上限和下限;同时,我们还对ZOPPM的通信和计算能耗进行对比实验,以评测通信和计算能耗对总能耗的影响情况。本文的实验环境为Pentium E5700(双核3.0 GHz)CPU,3 G内存;软件环境为 Windows XP操作系统,Eclipse和 Matlab;实验数据集为 Intel Lab Data[14]。
本文采用与文献[15]相同的能耗计算方法:无线通信电路发送和接收1 byte的能量消耗公式为es=α+γ×dk和er=β,其中,α为通信发送电路消耗的能量,γ为传输放大器消耗的能量,d为传输距离,k为路径损失因子,β为通信接收电路消耗的能量。我们采用文献[13]的参数:γ=10 pJ/bit/m2,α=45 nJ/bit,β=135 nJ/bit,k=2。此外,感知数据长度初始设置为10 bit,加密计算的初始能耗采用文献[8]给出的TelosB中利用RC4对10 bit数据进行加密的能耗数据8.92 μJ,并假设HMAC计算的能耗与加密计算相同。其它参数设置如表2所示。

表2 实验参数
在每一组实验中,我们通过在网络覆盖区域中随机分布感知节点,生成20组不同拓扑结构的网络(用不同的网络ID标识),进而通过计算20组网络的平均能耗值确定最值查询的总能耗。具体实验结果及分析如下:
(1)在实验设置的初始参数条件下,随机生成的20组网络的能耗实验结果如图1所示。
由图1(a)可知,在不同拓扑的网络中,ZOPPM和PMV-MQP的能耗均变化不大,且分布都较为均匀,但ZOPPM的能耗始终低于PMV-MQP。并且,与其能耗下限相比,ZOPPM平均节省约23.03%的能耗开销。由图1(b)可知,在ZOPPM的总能耗中,计算能耗Ecomp和通信能耗Ecomm的变化都不大,但通信能耗占总能耗的绝大部分(约99.96%)。可见,在随机生成的不同拓扑结构的网络中,ZOPPM和PMV-MQP的能耗均变化不大,但ZOPPM的能耗表现明显较优,其能量消耗绝大部分由数据通信产生。
(2)以感知节点数量n为自变量,其它参数保持初始设置不变,得到如图2所示的实验结果。
由图2(a)可知,随着感知节点数量n的增长,感知节点发送的数据消息也增多,导致ZOPPM和PMV-MQP的总能耗都显著增长,其中PMV-MQP的增长幅度较大,这是由于前者的任一查询单元中,仅有一个感知节点需要发送密文数据,而后者所有的感知节点却都需要发送。在本组实验设置下,ZOPPM的总能耗始终少于PMV-MQP,与后者的能耗下限相比,ZOPPM平均节省约23.05%的能耗开销。由图2(b)可知,在ZOPPM的能量消耗中,随着n的增长,Ecomm有显著增长,虽然Ecomp也同步增长,但由于其占总能耗的比重非常小(平均约占0.02%),其增长趋势不明显。
(3)以w为自变量,其它参数保持初始设置不变,得到如图3所示的实验结果。
由图3(a)可知,随着感知数据长度w的增大,ZOPPM和PMV-MQP的总能耗也随之增大,这是由于查询单元中的所有感知节点都需要传送HMAC数据,而w的长度与感知节点传送HMAC数据的数量成正比,因此,两者的总能耗都同步增长,但ZOPPM的总能耗始终少于PMV-MQP,与后者的能耗下限相比,ZOPPM平均节省约17.1%的能耗开销。由图3(b)可知,在ZOPPM消耗的总能量中,通信能耗占总能耗的绝大部分(平均约99.96%),计算能耗所占比重则非常小。
综合上述实验结果及分析可知:本文的ZOPPM的能耗优于文献[7]提出的PMV-MQP,在本文的实验设置条件下,ZOPPM比PMV-MQP的能耗下限平均节省近 20%的能量消耗;并且,在ZOPPM 协议中,收发数据的通信能耗占总能耗的绝大部分,而计算能耗所占的比重较小。
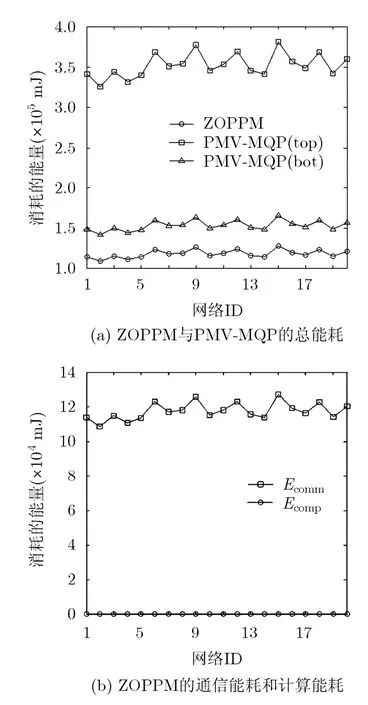
图1 不同网络拓扑下的能耗实验结果
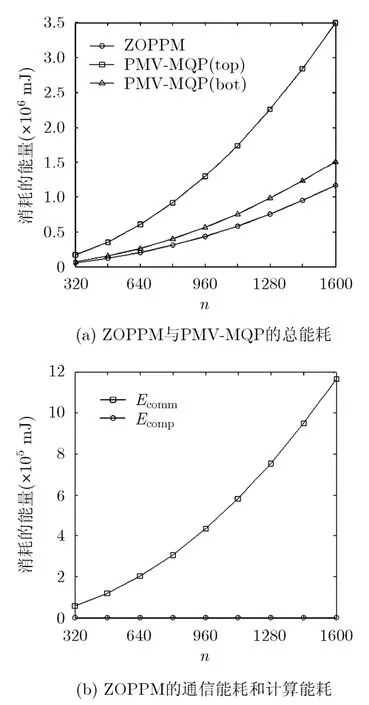
图2 以n为自变量时的能耗实验结果
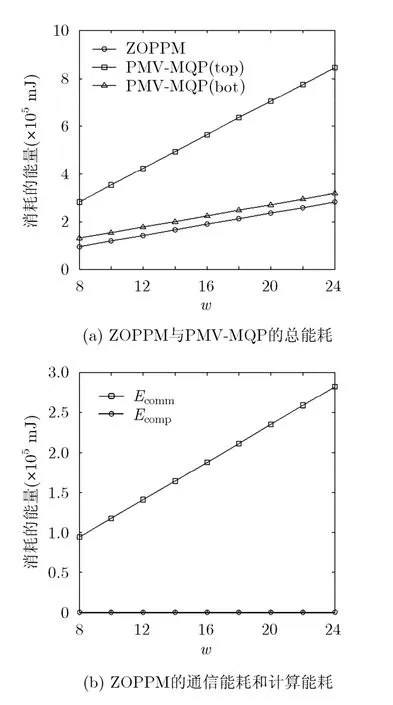
图3 以w为自变量时的能耗实验结果
6 总结
数据隐私保护问题是无线传感器网络中具有共性要求的问题,在诸如环境监测、医疗卫生、智能交通、国防军事等各种重要领域都有着迫切的需求,是无线传感器网络研究中的一个热点问题。然而,现有的两层WSNs重点关注范围等查询处理方法,对最值查询处理方法的研究相对较少。本文提出了一种基于Z-O编码的两层WSNs隐私保护最值查询处理协议。在该协议中,感知节点利用Z-O编码机制,并结合Hash消息身份验证编码方法,对本地感知数据进行HMAC数值化Z-O编码处理,并发送至存储节点;而存储节点则利用Z-O编码的数值比较特性,实现在无需感知数据明文参与下的数值线性关系比较,进而获得所在查询单元中产生局部最值的感知节点,并通知该感知节点计算并传送加密数据,然后构造局部查询结果并发送给Sink;最终由Sink完成最值查询结果的计算,并返回给用户。理论分析和实验结果表明,ZOPPM 协议能够确保感知数据和最值查询结果的隐私安全性,并且其能耗优于现有的方法。
[1]Gnawali O, Jang K Y, Paek J,et al.. The tenet architecture for tiered sensor networks[C]. Proceedings of the 4th ACM Conference on Embedded Networked Sensor Systems,Boulder, Colorado, USA, 2006: 153-166.
[2]Yang D, Misra S, Fang X,et al.. Two-tiered constrained relay node placement in wireless sensor networks: computational complexity and efficient approximations[J].IEEE Transactions on Mobile Computing, 2012, 11(8): 1399-1411.
[3]Chen F and Liu A X. SafeQ: secure and efficient query processing in sensor networks[C]. 29th IEEE International Conference on Computer Communications, San Diego, CA,USA, 2010: 1-9.
[4]Sheng B and Li Q. Verifiable privacy-preserving range query in two-tiered sensor networks[C]. 27th IEEE International Conference on Computer Communications, Phoenix, AZ,USA, 2008: 46-50.
[5]Shi J, Zhang R, and Zhang Y. Secure range queries in tiered sensor networks[C]. 28th IEEE International Conference on Computer Communications, Rio de Janeiro, Brazil, 2009:945-953.
[6]Shi J, Zhang R, and Zhang Y. A spatiotemporal approach for secure range queries in tiered sensor networks[J].IEEE Transactions on Wireless Communications, 2011, 10(1):264-273.
[7]Yao Y, Xiong N, Park J H,et al.. Privacy-preserving max/min query in two-tiered wireless sensor networks[OL].Computers & Mathematics with Applications. http://www.sciencedirect.com/science/article/pii/S08981221120011 74. 2012, 2.
[8]Groat M M, Hey W, and Forrest S. KIPDA:kindistinguishable privacy-preserving data aggregation in wireless sensor networks[C]. 30th IEEE International Conference on Computer Communications, Shanghai, China,2011: 2024-2032.
[9]Lin H Y and Tzeng W G. An efficient solution to the millionaires’ problem based on homomorphic encryption[C].Proceedings of the 3rd International Conference on Applied Cryptography and Network Security, New York, NY, USA,2005: 97-134.
[10]Krawczyk H, Canetti R, and Bellare M. HMAC:keyed-hashing for message authentication[R]. RFC 2104,1997.
[11]Yao A C. Protocols for secure computations[C]. 23rd Annual Symposium on Foundations of Computer Science, Chicago,Illinois, USA, 1982: 160-164.
[12]Bozovic V, Socek D, Steinwandt R,et al.. Multi-authority attribute-based encryption with honest-but-curious central authority[J].International Journal of Computer Mathematics,2012, 89(3): 268-283.
[13]Coman A, Sander J, and Nascimento M A. Adaptive processing of historical spatial range queries in peer-to-peer sensor networks[J].Distributed and Parallel Databases, 2007,22(2): 133-163.
[14]Samuel M. Intel lab data[OL]. http://db.csail.mit.edu/labdata/labdata.html. 2004.6.
[15]Coman A, Nascimento A M, and Sander J. A framework for spatio-temporal query processing over wireless sensor networks[C]. Proceeedings of the 1st International Workshop on Data Management for Sensor Networks, Toronto, Canada,2004: 104-110.

