基于分块自适应压缩感知的可逆水印算法
张秋余 孙 媛 晏 燕
(兰州理工大学计算机与通信学院 兰州 730050)
1 引言
近年来,在医学诊断、军事图像和遥感图像处理等数据准确性要求较高的应用领域中,国内外学者进行深入研究,提出了可逆水印技术。该算法除具备传统数字水印特点外,还可在水印系统接收端无失真地恢复原始载体图像信号。该技术通常需要满足一些技术要求[1],如不可见性、高容量、安全性等。
可逆水印最早出现在 1999年柯达公司的一项美国专利[2]中,利用求模的嵌入方法在图像中嵌入数据,使得提取算法在恢复嵌入数据的同时,还能够完全得到原始图像,但该方法嵌入容量较小。一般来说,可逆水印算法的性能评估主要体现在嵌入容量和不可见性。鉴于此,国内外学者提出一系列算法。如基于直方图平移算法[3-5],基于压缩技术的算法[6],基于整数变换的算法[7-10]。然而,对于单嵌入过程的算法,很少有嵌入率达到1.0 bpp。为提高可逆水印算法的嵌入容量,文献[11]在文献[12]的基础上提出一种高容量可逆水印算法,当采用“Lena”图像为载体时,其嵌入率达到了1.7 bpp。文献[13]提出多种可逆水印算法以提高水印嵌入容量。文献[14]在此基础上改进了文献[13]提出的利用奇偶特性、和值不变特性和差值调节的可逆水印方案。但是,这些算法大多数具有高嵌入容量而失真大的特点,不利于可逆水印算法的实际应用。
针对上述问题,本文提出一种基于分块的高容量自适应压缩感知可逆水印算法(BACS-RWA)。将载体图像分成互不重叠的小块,利用周围块与目标块统计特性判断目标块类型,将这些块分成3类:光滑块集合 、普通块集合、复杂块集合。复杂块不嵌入水印以增强不可见性,光滑块和普通块进行压缩感知后,自适应地压缩感知嵌入水印从而提高水印嵌入容量。
2 相关理论知识
2.1 采用分块思想的优势
现有可逆图像水印算法中,水印嵌入阶段大多是把整幅图作为处理对象,进行统一操作,该类算法主要存在两点不足:一方面,在自然图像中,局部区域的特征与整幅图表现出的特征常有不同,在利用整幅图的特征确定相关参数时局部特征常被忽略掉,而从整幅图的特征得到的可逆图像水印嵌入参数、灰度溢出控制参数等并不能保证适用于局部区域的最佳参数;另一方面,不同图像区域水印嵌入能力会有差别,全图统一处理的方式没有充分利用这种特性,通常是不加区分地统一对待不同特性的区域。
采用基于图像分块思想的可逆水印算法,通过操作对象区域化,各区域操作相互独立,可以改善以上采用全图统一操作不足,增加可逆图像水印算法的性能。
2.2 块类型的划分
首先将载体图像进行分块,并计算各图像块方差和均值。本文通过目标图像块与其周围图像块差值与预设阈值的关系,判断不同图像块纹理复杂程度,从而嵌入不同数据。预设两个阈值 TH1, TH2(TH1≥TH2),图像块分布如图 1所示,再通过周围块的方差对目标块进行判定其是平滑块、普通块、复杂块。整个过程见图2,其判定方法如下:

图1 目标块与相邻块分布
情况 1((V1≤TH2)&&(V2≤TH2)&&(V3≤TH2)&&(V4≤TH2)):块 0(目标块)判为平滑块。其中V1, V2, V3, V4分别表示块1,块2,块3,块4的方差值。
情况 2(V1, V2, V3, V4中至少有一个大于TH2,且小于TH1):块0 判为普通块。
情况 3((V1≥TH1)&&(V2≥TH1)&&(V3≥TH1)&&(V4≥TH1)):块0 判为复杂块。
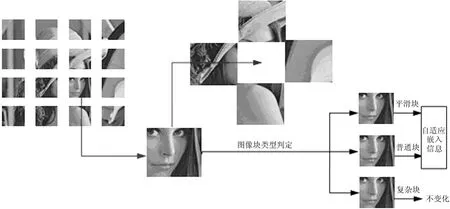
图2 块类型划分过程
2.3 基于分块的压缩感知
Candés和 Donoho于2006年正式提出了压缩感知(Compressed Sensing, CS)的概念,该理论突破了经典香农定理的瓶颈。其核心思想是将压缩与采样合并进行,首先采集信号的非自适应线性投影(测量值),然后根据相应重构算法由测量值重构原始信号。优点在于信号的投影测量数据量远远小于传统采样方法所获的数据量,使得高分辨率信号的采集成为可能。
大尺度整幅图像采样时,现有 CS方法存在计算复杂度高、存储压缩采样算子所需存储器规模大、重建时间长等问题,采用基于分块的压缩采样方法则能够实现较好的性能折中[15]。
首先将Ir×Ic维图像X分成大小为B×B的小块,xi为第i个块的向量信号,i=1,…,n,n=N/B2,n为块数,N为像素数且满足N=nr×nc;然后对每个块采用相同的压缩采样算子,得到每个图像块的测量值向量yi,即
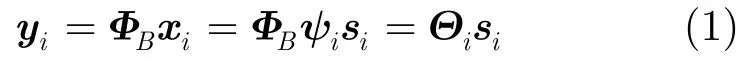

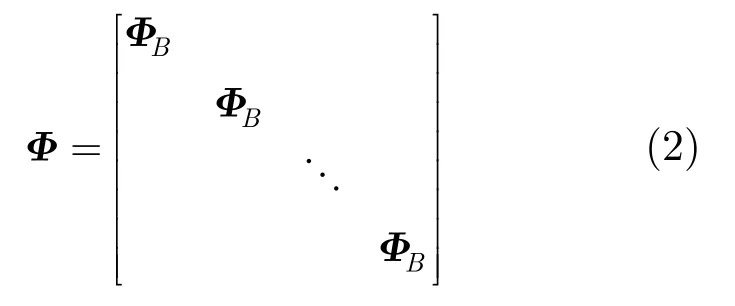
在分块CS算法中仅需存储ΦB,而不需存储整幅图像的测量矩阵Φ。采用l2范数意义下的优化问题求解,则每个块的重构过程可表示为如式(3):
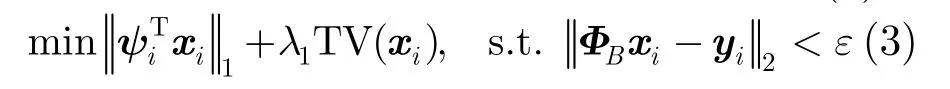


式(4)中λ2是权重系数,在数据一致性与稀疏性之间进行权衡。本文在正交小波基下进行稀疏化,高斯矩阵作为测量矩阵,采用非线性共轭梯度算法和带回溯线搜索进行优化目标的重构[16]。
2.4 整数变换

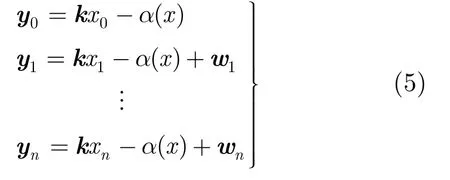
其中n,k是两个整数且n≥1,k>1,α(x)是个可逆整数函数,定义如下:

整数逆变换:
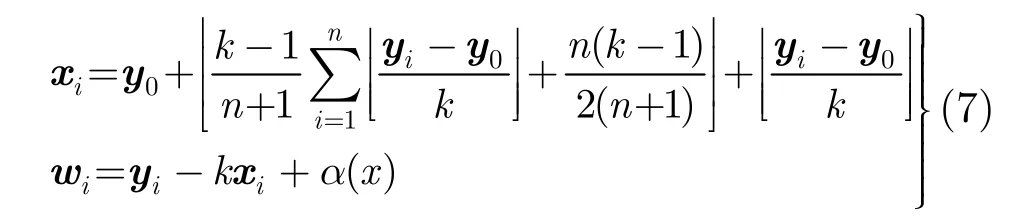
式(7)中x,y分别代表给定像素块的原始值和嵌入水印后的值,w代表嵌入的信息。
2.5 自适应整数变换
式(5)中基于整数变换的嵌入失真可以表示为式(8)的形式。


为避免数据溢出,设B={x=(x0,x1,…,xn)∈Zn:0≤xi≤255}是大小为n+1所有灰度图像的像素值数组,其子集为

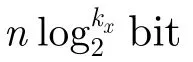
因此,自适应整数变换过程可由式(5)更改为如下:

综上可见,嵌入容量参数kx主要由分块类型及方差决定,方差越小,块越平滑,失真也小。故本文自适应地选择kx,在相应的块中嵌入大量水印信息,以提高水印嵌入容量,保证较好的图像质量。

表1 kx的自适应选择过程
3 BACS-RWA算法实现过程
3.1 嵌入算法步骤
步骤 1 将载体图像X分成N个非重叠小块x=(x0,x1,…,xn)∈Z n+1,xi是x中任一块;
步骤 2 按照2.2节方法将所得小块分为3类块的集合:滑块集合I1,普通块集合I2,复杂块集合I3;

步骤 4 根据上一步建立比特序列记录Location Map(LM),其中

同时采用行程编码(Run-Length Encoding,RLE)对LM进行无损压缩得到CLM。
嵌入算法的伪代码过程如表2所示。

表2 嵌入算法的伪代码过程
3.2 提取算法步骤
水印提取算法流程图如图3所示。
步骤 1 将水印图像Iw分成N个非重叠小块Iw=(iw0,iw1,…,iwn)∈Zn+1,iwi是Iw中任一小块;
步骤 2 用与嵌入过程中光栅扫描顺序相反的顺序即从左到右,从上到下进行扫描图像块,读取iwi的LSB,得到压缩的位置图CLM;

图3 水印提取算法流程图
步骤 3 解压 CLM 即得位置图 LM,从而得TH1, TH2,T,据此判断出块类型,分为光滑块I1,普通块I2、复杂块I3;
步骤 4 对得到的复杂块I3不做处理,利用2.3节基于块压缩感知的重构方法对平滑块I1,普通快I2利用重构算法进行块重构,得出压缩感知后的随机投影测量值;
步骤 5 根据步骤 3得到位置图相关信息确定各块的容量参数kx,对步骤4中I1,I2的重构结果进行自适应整数逆变换即可得到水印信息w和原始载体I。
4 实验结果及分析
所有实验均在 Dell Inspiron N4010笔记本电脑,i3 CPU, 2 G内存,Win7操作系统下以MATLAB7.8为实验平台得到。选择4幅标准的具有不同纹理特征的512×512的8 bit灰度载体图像如图 4(a)-4(d),包括 Lena, Baboon, Plane(F-16)和Sailboat,采用随机函数(rand)随机生成的随机比特序列作为水印信息,性能评价标准以数据嵌入比特率(BPP)和峰值信噪比(PSNR)来衡量。
4.1 阈值的选择
为提高水印嵌入容量,本文进行了2×2, 4×4, 8×8, 16×16分块实验。现以其一种情况为例说明阈值选择,其它分块情况原理相同。首先计算4类载体图像分块后对应的每个块中各像素的均值(mean)和方差(var),如表 3,对应块号的数字组成顺序就是其分块后行列号。当分块为16×16时,分别对4种情况的方差和均值进行了相应计算并用于实验中阈值,权衡水印容量、图像质量及算法综合性能,自适应容量参数选择中T取表3结果的4类载体块方差的均值1.3229e+003, TH1, TH2分别设为相应载体的方差的最大值和最小值,据文中判定方法可确定块类型。
4.2 不同分块数目对算法性能的影响
图5以Lena为例可以看出由分块2×2到4×4时,嵌入容量较高且图像不可见性能较好。然而当增加到 8×8时性能居两者之间,当分块为 16×16时 PSNR 值略高于 4×4,最大嵌入容量达到 1.8 bpp,而其它分块最大嵌入容量均低于此值。其主要原因一方面在于块越大嵌入率就越大,但分块太大的话不能嵌入的点比较多,从而位置图比较大;另一方面由于本算法中采用了分块压缩感知理论,不同分块尺寸会影响重建效果和时间。随着分块尺寸的减小,在重建图像中子空间(或块)的边界更容易形成明显的块边界,视觉效果逐渐降低,得出的峰值信噪比也逐渐降低,当分块为16×16时其重建效果较好且重建时间适中,故表现出最优性能。而 8×8分块重建时,块效应相对较突出,影响了其重建质量。
本文采用了4幅载体图像分别进行了2×2, 4×4, 8×8, 16×16分块嵌入,其对应的最大嵌入率如图6所示,经多次实验得最佳分块为16×16分块。采用本文嵌入算法后最大嵌入率也有差异,其中Lena为1.8 bpp, Baboon为0.8 bpp, Plane为1.87 bpp, Sailboat为1.6 bpp。
4.3 算法综合性能与其他文献方法比较
为验证 BACS-RWA算法的优越性,实验选择16×16分块,采用相同载体图像和水印,选取文献[17],文献[18]和文献[19]3种可逆水印算法进行对比实验。从图7(a)-7(d)综合性能对比实验结果可以看出,BACS-RWA具有较好的水印容量-失真性能。
图 7(a)是基于局部水印嵌入能力差别较小的Lena图像的综合性能对比曲线图。在高嵌入率下的质量较高,其PSNR值在嵌入率高达1 bpp时仍高于35 dB;当嵌入率小于0.4时,文献[19]的算法在分块处理表现出的效果不太明显,PSNR性能略低于文献[18]算法,而文献[17]算法性能在 1 bpp范围内都低于其他算法,这是因为其灰度溢出采用的是灰度直方图最小合并项合并压缩的方案。本文算法最高嵌入容量可达到1.8 bpp,文献[19]算法嵌入容量不足 1.4 bpp,文献[18]算法嵌入容量不足 1.2 bpp,而文献[17]最大嵌入容量仅1 bpp。

图4 实验采用的载体图像

表3 不同载体图像4×4块均值和方差

图5 Lena 进行不同分块性能曲线
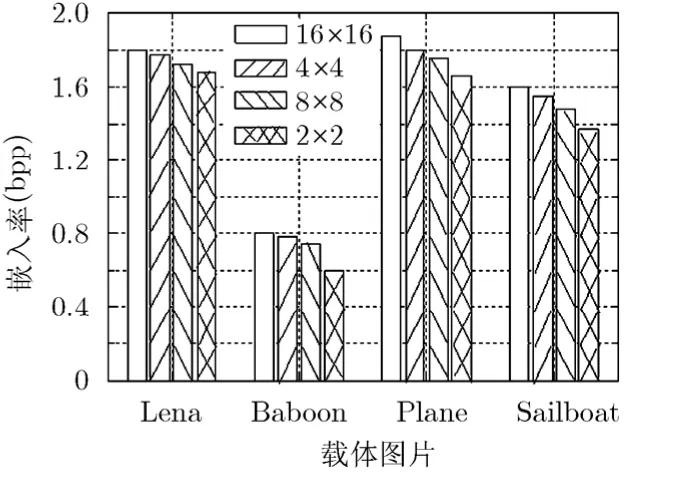
图6 不同载体进行4种分块的嵌入率
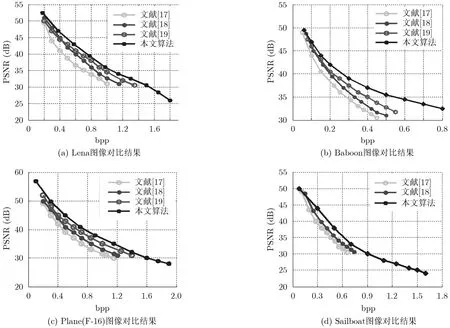
图7 算法综合性能对比
图7(b)是基于载体图像为Baboon的综合性能对比曲线。由于Baboon是4幅图像中纹理最复杂的图像,图像的质量随着嵌入数据量的增多下降较快,在嵌入率为0.1 bpp时4种方法PSNR值差异不明显,当嵌入率达到0.4 bpp时,利用BACS-RWA嵌入数据后的图像的 PSNR比文献[19],文献[18]和文献[17]算法分别高2 dB, 4 dB, 5 dB,表现出了良好的性能。随着嵌入信息量的增多,复杂的纹理对图像质量影响越来越严重,但其PSNR仍高于其他算法。
图7(c)采用了纹理较为简单的Plane(F-16)为载体图像,图像整体相对于其它3种载体最平滑,像素块的差值小,使用较小的阈值则可以将图像划分成不同的类型,平滑区域能产生较多的嵌入信息可用像素。因此,嵌入率比较高,图像质量较好,综合性能较稳定。而另外3种算法当嵌入率达1.2 bpp附近时图像的PSNR均达到了30 dB,在嵌入率为0.7 bpp附近时,文献[19]算法与本文算法性能相差较小,本文算法最大嵌入率达到最大值1.87 bpp。
图7(d)是对Sailboat进行实验对比结果,嵌入率在0.2 bpp附近时文献[18]算法PSNR值略微高于本文算法,但随着其嵌入率的增大,文献[18]和文献[17]算法的PSNR值明显下降,而文献[19]算法中未对该载体图进行实验,本文算法的综合性能曲线则较平稳,且当达到最大嵌入率时其PSNR值依然高于24 dB。
本文选取3个固定嵌入率0.5 bpp, 1.0 bpp和1.2 bpp进行相应的PSNR对比,结果如表4所示。
表4中的“-”表示由于图像本身特性无法进行相应实验测量。从表中可以看出,在所选嵌入率相同的情况下,当在嵌入率为0.5 bpp时,本文算法的平均PSNR高于文献[18]2.84 dB,高于文献[19]2.1 dB;随着嵌入率升高,当达到1.0 bpp时,本文算法平均PSNR高于文献[18]2.3 dB,高于文献[19]1.3 dB;在相同嵌入率为 1.2 bpp时,本文算法平均PSNR分别高于文献[18]3.15 dB,高于文献[19]1.45 dB。出现此差异主要原因是文献[17]采用的线性预测误差相比其他算法的预测误差要发散,相比而言,该算法性能稍差,但性能比较平稳,这归功于其灰度直方图调整采用了最小合并项的方案。文献[18]采用基于直方图位移的插值技术的可逆图像水印,由于取得较集中的预测误差直方图,在小嵌入量时算法性能较高,但不足的是灰度溢出控制方案对于在最亮或最暗端含有较大比例像素的宿主图像,由于辅助信息无法完整保存导致嵌入失效。文献[19]在水印嵌入能力强的局部区域水印分配的多,嵌入弱的分配的少,但其通过迭代处理后不可避免地产生了失真从而影响图像质量。由此可见,本文算法具有较好的图像质量,适于高容量水印信息嵌入。
5 结束语
本文提出一种基于分块自适应压缩感知的数字图像可逆水印算法。利用分块理论判断块类型并进行压缩感知,自适应选择嵌入容量系数进行整数变换嵌入信息,以提高水印容量。避免了噪声块引起的较大失真,更多的水印嵌入到光滑块和普通块中,提高了水印嵌入容量同时确保了图像质量,不可见性较好。实验结果表明:该算法较以往可逆水印算法相比在嵌入容量和不可见性等综合性能上都具有优越性。

表4 相同嵌入率下 PSNR值对比(dB)
[1]Tian J. Reversible data embedding using a difference expansion[J].IEEE Transactions on Circuits System Video Technology, 2003, 13(8): 890-896.
[2]Honsinger C W, Jones P, Rabbani M,et al.. Lossless recovery of an original image containing embedded data[P]. US,Patent, US006278791B1, 2001-08-21.
[3]Tai W L, Yeh C M, and Chang C C. Reversible data hiding based on histogram modification of pixel differences[J].IEEE Transactions on Circuits System Video Technology, 2009,19(6): 906-910.
[4]Chung Kuo-liang, Huang Yong-huai, Yan Wen-ming,et al..Distortion reduction for histogram modification-based reversible data hiding[J].Applied Mathematics Computation,2012, 218(9): 5819-5826.
[5]王俊祥, 倪江群, 潘金伟. 一种基于直方图平移的高性能可逆水印算法[J]. 自动化学报, 2012, 38(1): 88-96.
Wang Jun-xiang, Ni Jiang-qun, and Pan Jin-wei. A high performance reversible watermarking scheme based on histogram shifting[J].Acta Automatica Sinica, 2012, 38(1):88-96.
[6]Celik M U, Sharma G, Tekalp A M,et al.. Lossless generalized-LSB data embedding[J].IEEE Transactions on Image Processing, 2005, 14(2): 253-266.
[7]Peng Fei, Li Xiao-long, and Yang Bin. Adaptive reversible data hiding scheme based on integer transform[J].Signal Processing, 2012, 92(1): 54-62.
[8]Alattar A M. Reversible watermark using the difference expansion of a generalized integer transform[J].IEEE Transactions on Image Processing, 2004, 13(8): 1147-1156.
[9]朱立, 赵耀, 倪蓉蓉. 基于混合整数变换的高容量可逆数字水印[J]. 数据采集与处理, 2010, 25(2): 188-194.
Zhu Li, Zhao Yao, and Ni Rong-rong. High-capacity reversible watermarking based on mixed integer transform[J].Journal of Data Acquisition and Processing, 2010, 25(2):188-194.
[10]Arsalan M, Malik S A, and Khan A. Intelligent reversible watermarking in integer wavelet domain for medical images[J].Journal of Systems and Software, 2012, 85(4):883-894.
[11]Chaumont M and Puech W. A high capacity reversible watermarking scheme[C]. Proceedings of the SPIE-IS&T Electronic Imaging, Visual Communications and Image Processing, San Jose, California, USA, Sept. 11-12, 2009,SPIE Vol. 7257: 1-9.
[12]Coltuc D. Improved capacity reversible watermarking[C].Proceedings of the 14th IEEE International Conference on Image Processing(ICIP’07), San Antonio, TX, USA, Sept. 16-Oct. 19, 2007, Vol.3: 249-252.
[13]翁韶伟. 数字图像的高容量可逆水印研究[D]. [博士论文]. 北京交通大学, 2009.
Weng Shao-wei. Research on high-capacity reversible watermarking algorithms[D]. [Ph.D. dissertation], Beijing Jiaotong University, 2009.
[14]吕林涛, 张玺. 改进的大容量可逆数字水印嵌入算法[J]. 计算机工程, 2011, 37(22): 107-109.
Lv Lin-tao and Zhang Xi. Improved large capacity reversible digital watermark embedding algorithm[J].Computer Engineering, 2011, 37(22): 107-109.
[15]赵春晖, 刘巍. 基于分块压缩感知的图像半脆弱零水印算法[J]. 自动化学报, 2012, 38(4): 609-617.
Zhao Chun-hui and Liu Wei. Block compressive sensing based image semi-fragile zero-watermarking[J].Acta Automatica Sinica, 2012, 38(4): 609-617.
[16]Lustig M, Donoho D L, and Pauly J M. Sparse MRI: the application of compressed sensing for rapid MR imaging[J].Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195.
[17]Tsai P, Hu Y C, and Yeh H L. Reversible image hiding scheme using predictive coding and histogram shifting[J].Signal Processing, 2009, 89(6): 1129-1143.
[18]Luo Li-xin, Zheng yong, Chen Ming,et al.. Reversible image watermarking using interpolation technique[J].IEEE Transactions on Information Forensics and Security, 2010,5(1): 187-193.
[19]罗剑高. 可逆图像水印及可逆图像认证技术研究[D]. [博士论文], 华南理工大学, 2011.
Luo Jian-gao. Research of reversible image watermarking and reversible image authentication techniques[D]. [Ph.D.dissertation]. South of China University of Technology, 2011.

