基于图形电磁学的近场角闪烁预估方法研究

刘立国 莫锦军 付云起 袁乃昌

(国防科技大学电子科学与工程学院 长沙 410073)

1 引言

雷达目标角闪烁是由于雷达扩展目标中各散射单元间的相互影响，是目标角度测量和角度跟踪上的固有误差源[1]。角闪烁误差属于目标噪声，是雷达目标的一种固有特性，与雷达系统无关。角闪烁误差通常用角闪烁线偏差来表征，远场条件下这种线偏差与观察雷达远近无关，是目标的特征量。目标角闪烁起源于扩展目标，从目标特性研究的观点来看，凡是尺度能和波长相比拟，具有两个或两个以上散射中心的都属于扩展目标，都会产生角闪烁线偏差[2]。角闪烁主要对雷达的跟踪精度产生较大影响，一般的理论研究和工程应用都集中在远场条件下的角闪烁预估、验证等[3-5]。实际中，对雷达跟踪影响更大的是近场条件下的角闪烁，此时雷达与目标距离较近，对角度跟踪误差的影响更大。研究近场条件下的角闪烁更加具有实际的工程应用价值。特别当雷达与目标的距离使得雷达波束不能够完全覆盖目标时，角闪烁预估对于目标的打击毁伤效果预估具有很大作用，而此情况下的角闪烁研究尚未见诸其它文献。

图形电磁学(GRECO)[6-8]作为一种重要的电磁仿真方法，与其它方法[9,10]相比较，由于其在仿真电大目标上的优势而受到青睐。图形电磁学结合了传统高频方法和计算机图形学，采用计算机图形学的目标渲染功能从而省去了在传统高频方法中耗时的可见面判断与网格剖分过程。利用物理光学法来计算每个可见面对电磁散射的贡献，采用物理绕射方法计算棱边对电磁散射的贡献。GRECO方法利用显卡的深度缓存算法来实现不可见面的消隐，达到了加速仿真计算进程的目的。利用渲染过程的栅格化过程代替面元剖分过程、渲染生成的像素代替传统高频方法中的面元，既节省了内存又极大地加快了仿真速度。

由于GRECO算法具有计算实时性强的优点，使其成为电大目标上特性仿真的重要工具。其广泛应用于SAR, ISAR的研究和远场角闪烁的计算[11,12]。利用提取的目标散射中心计算目标近远场的角闪烁特性的研究见诸文献[13-15]，目标散射中心的提取耗时长，计算资源需求多。本文将GRECO方法用于近场目标的角闪烁特性计算，得到了针对通用目标的解析计算方法从而省略了散射中心提取的过程。

2 近场RCS计算

2.1 相对远近场概念

目标处于雷达的远场区或者近场区不仅取决于目标的几何尺寸、姿态，还与雷达的工作波长有关。定义远场距离为

其中D是目标的最大长度，λ是雷达工作波长。当雷达目标之间的距离满足R＞Rlim时，目标处于雷达的远场区域，一般的研究和工程应用中都假设目标处于远场区域，此时满足平面波近似假设，使得处理简化。

2.2 近场RCS

近场条件下入射平面波条件不再成立，入射到目标的电磁波不能视为平面波，一般情况下雷达口径远小于目标尺寸，故而入射电磁波可视为球面波[16]，雷达、目标的坐标关系如图1。

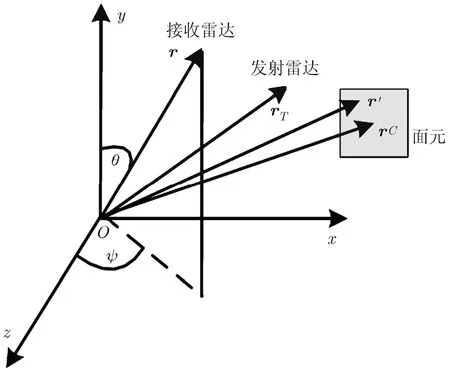
图1 雷达、面元位置关系

入射电场可表示为

其中ei(r')表示面元内任意r'处的电场单位矢量，rT表示发射雷达的位置矢量，rC表示第i个面元中心位置，r0是入射电场值为E0时的参考距离。在散射体表面，从上节讨论的结论可知此时散射中心仍处于远场区，入射电磁场可视为局部平面波：

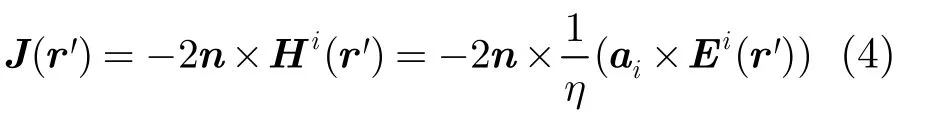
其中η为自由空间波阻抗。可得散射场为

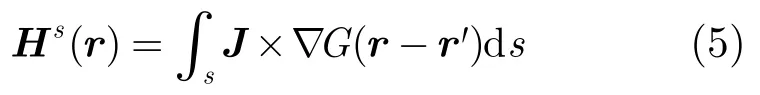
其中G自由空间的格林函数。在剖分面元为矩形时得到其复雷达散射截面为

整个目标的近场雷达散射截面可通过式(7)计算得到：

3 近场角闪烁计算推导

3.1 近场回波相位

目标角闪烁确定性模型的计算方法有两种，即坡印廷矢量法和相位梯度法。在实际测量中所得到的是目标回波的幅度和相位信息，而不是坡印廷矢量。相位梯度法主要用于实验测量和工程分析中，而坡印廷矢量法主要用于理论分析和计算。当目标满足几何光学条件近似时，这两种方法是等价的[17]。本文中采用的是相位梯度方法进行计算。

如2.1节所述，目标的散射中心满足远场条件，目标回波信号为

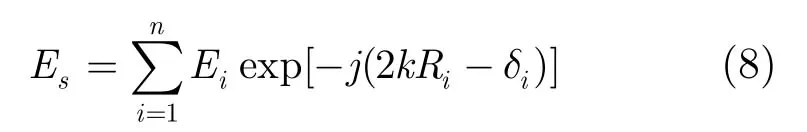
其中Ei是电压的反射值，δi是散射中心的初始相位，Ri表示雷达与第i个散射中心的距离：

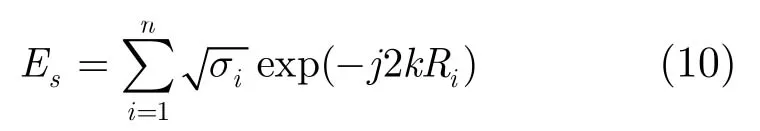
进一步可得到其回波信号的相位为

3.2 近场角闪烁计算

获得目标回波信号的相位信息后，利用相位梯度法即可计算相应的角闪烁线偏差。但是由于远场条件不再成立，不能利用Taylor展开对式(9)进行展开近似，本文采用精确的计算方法。

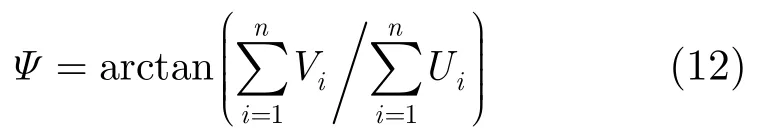
通过式(12)求得其全导数为

其中dRi表示为球坐标下Ri的全导数：

全导数的各个分量解析式如下：

通过式(15)-式(19)即可得到回波相位的全导数为

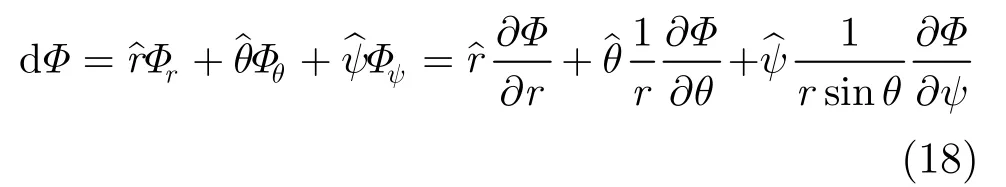
全导数中的各个分量如式(19)-式(21)。

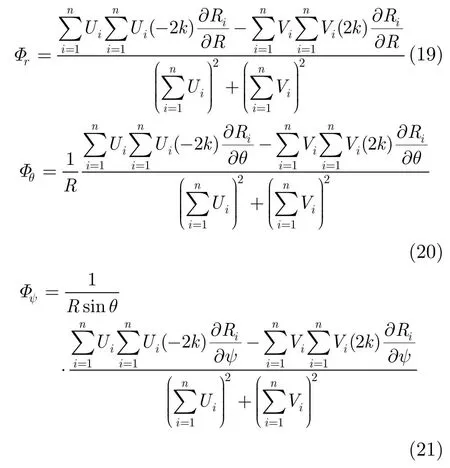
进而可以求得近场情况下的角闪烁线偏差的计算公式为

式(22)，式(23)即为计算角闪烁线偏差的通用公式。GRECO计算目标特性时采用的是固定雷达，旋转目标的方法。即雷达固定在z轴，此时图 1中的θ=π/2,ψ=0，代入计算公式可使其得到简化。

3.3 雷达照射范围获取

图2 雷达波束与目标范围关系

近场条件下的角闪烁不仅与角度有关，还与雷达、目标之间的距离有关。随着距离的减少，目标从远场区到近场区，最后进入雷达波束部分覆盖区。如图2所示，假设雷达波束处于水平面，雷达距离目标R，目标在雷达的视线的垂直方向最大尺度为L，雷达的半波束角为Ψ。容易得到如下的结论：2RtanΨ＞L时，雷达波束能够完整地照射目标，反之则只有部分目标被照射到，照射的区域为±Rt anΨ。俯仰面同理可以求得。为了简化计算，部分照射时假设雷达波束指向目标的几何中心。在实际应用中，为了更加方便地计算，采取选择旋转目标、固定雷达的方法，设定一个固定的包围盒进行目标渲染即可。

4 算法的验证与应用

角闪烁线偏差的验证方法可分为两种：实验验证与理论计算验证。实验验证方法具有通用性强，验证体选择广泛等优点，但是其对设备、实验环境等的要求较高。理论计算验证可通过采用具有解析解的模型进行理论计算，与仿真数值进行比较。具有角闪烁线偏差解析解的模型有限，因而验证体的选择存在困难，但是理论计算具有验证准确，勿需多次重复的优点。本文采用地理论验证的方法。

4.1 远场验证

4.2 近场渐近与负相关性验证

图3 两金属球模型

图4 两金属球远场角闪烁线偏差结果对比

当雷达与目标的距离满足远场条件时，此时近场区角闪烁数值应与远场条件下计算的数值基本一致，因此可计算距离渐变的角闪烁线偏差，随着距离的增大，近场角闪烁线偏差与远场结果趋于一致。这是一种直观且朴素的物理思想，也是经常应用于科学验证的一种方法。采用3金属球模型，如图5所示。 3金属球的球心排列在一条直线上，金属球的直径分别为dA=9.75 cm,dB=7.50 cm,dC=10.75 cm，金属球A和B的间距为30 cm，金属球B和C的间距为40 cm。计算时设置其型心为参考点，水平极化入射的平面波频率为10 GHz，，角度范围0°-10°，分别计算了距离为50 m, 1 km和远场的角闪烁线偏差，结果如图6，此时的远场条件约为2 km。随着距离的增大，计算结果逐渐接近远场结果，在距离为1 km，两者的变化趋势一致重合， 验证了渐近的变化趋势。从图中也看出，在不满足远场条件时，距离的不同会导致角闪烁数值的差异，距离越近这种差异越大，近场角闪烁与远场角闪烁有着迥然不同的变化趋势。

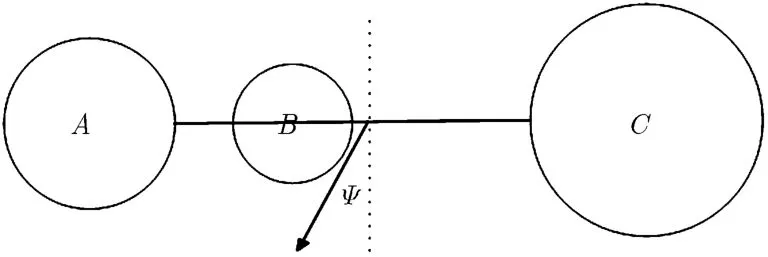
图5 3金属球模型

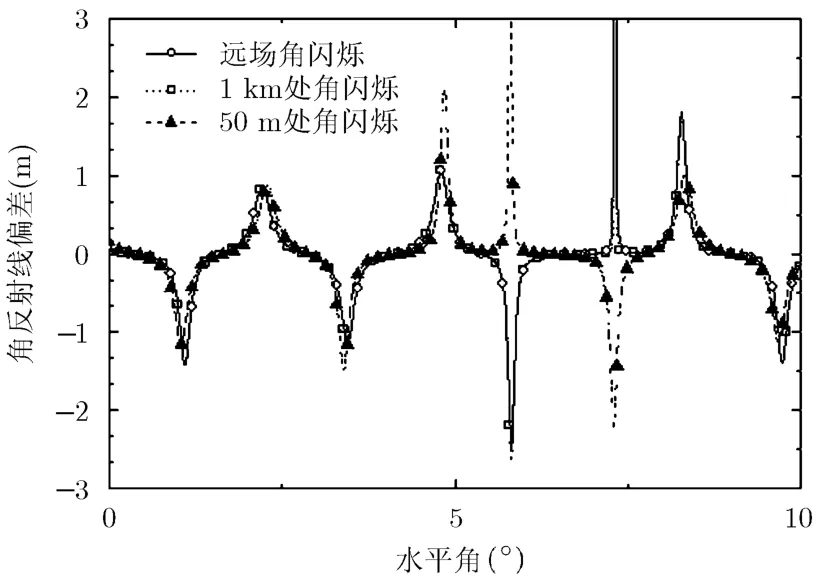
图6 3金属球近场角闪烁线偏差结果

角闪烁与雷达散射截面(RCS)是具有关联的，目前这种关联还未有明确且统一的结论，但是角闪烁与RCS的负相关性是被普通认同的，也是综合考虑二者关系的重要依据，采用这种负相关性的验证方法可以间接地证明计算方法的准确性。采用图5所示的3金属球模型，计算频率10 GHz，水平极化入射，角度范围0°-10°，计算了距离为100 m时的近场角闪烁线偏差与近场RCS的关系，为了使得结果的对比更加直观、清晰，对角闪烁的数值做了如下处理：glint=10·lg(abs(glint))，比较的结果如图7。直线加矩形曲线为角闪烁线偏差数值结果，直线加空心圆曲线为近场RCS变化趋势，从图中看出，在大角闪烁位置处的近场RCS总是处于波谷，两者存在负相关性特征。对于3金属球等简单目标这种负相关性是显著的。

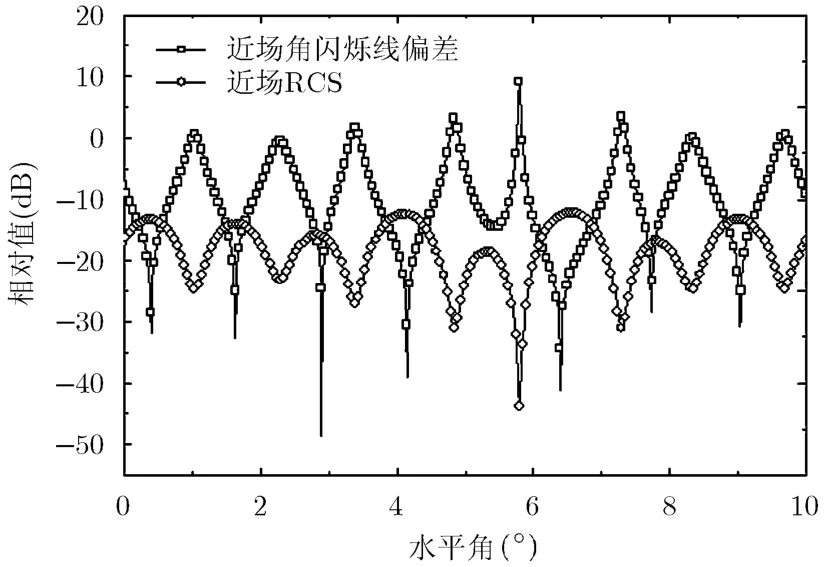
图7 雷达散射截面与角闪烁负相关性验证

4.3 复杂目标角闪烁仿真计算

以基德级驱逐舰为例来计算其近场角闪烁线偏差，基德级是目前国际上现役的主战舰船，计算其角闪烁特性有着重要的学术和工程意义。基德级驱逐舰的模型如图8所示，其舰长171.7 m，全宽16.8 m，吃水深度9 m。

图8 基德级驱逐舰模型

计算频率为10 GHz，水平极化入射，天线的水平波束角和俯仰波束角都是8°，基德级驱逐舰的远场距离为30 km，部分覆盖时的最大距离为1 km。因此雷达跟踪时的大部分时间处于近场范围内，需计算近场的角闪烁线偏差才能准确估计其跟踪误差。特别是当雷达、目标之间的距离在1 km之内时雷达波束已经不能覆盖目标，此时需考虑部分照射的情况。选取了距离为2.5 km, 1.5 km和0.5 km作为典型值计算其角闪烁特性，距离为0.5 km时需考虑部分照射的情况。计算结果如图9所示，从结果对比中发现波束覆盖与部分照射时的偏差较大，且对雷达的跟踪误差影响较大。由于采取目标的几何中心作为参考点，大部分角度内跟踪误差并未使跟踪方向偏离目标，但是其对于瞄准误差有着显著的影响。

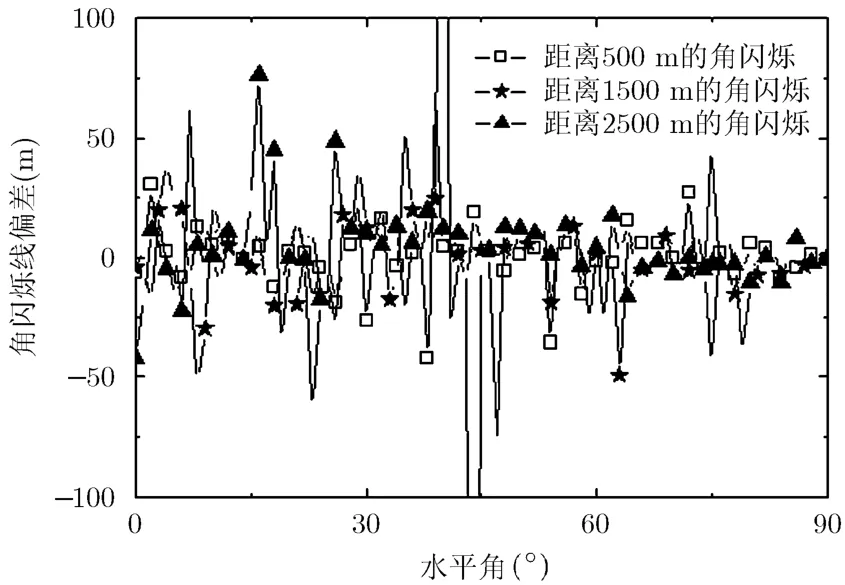
图9 基德级驱逐舰近场角闪烁计算结果

5 结束语

本文在详细推导近场角闪烁计算公式的基础上，首次将GRECO算法应用于近场角闪烁的计算与预估，给出了其解析的计算方案。解析计算方法仅需利用GRECO计算目标的近场RCS即可得到目标近场角闪烁的数值，其计算的准确性完全取决于近场RCS的计算准确性。通过远场验证、近场渐近验证和负相关性验证等间接方法，验证了本文方法的正确性。首次考虑了雷达波束不完全覆盖目标的情况，更具有实际的工程意义和应用价值。考虑计算的实时性和计算资源的需求，目前的仿真计算仅考虑了目标的一次反射；多次反射可利用迭代物理光学法(IPO)实现，如何在减少计算的需求的情况下实现多次散射的计算是未来的研究方向。

[1]黄培康, 林桂森, 樊正芳, 等. 雷达目标特征信号[M]. 北京:宇航工业出版社, 1993: 79-115.

[2]殷红成, 黄培康, 王超. 再论扩展目标的角闪烁[J]. 系统工程与电子技术, 2007, 29(4): 499-504.

Yin Hong-cheng, Huang Pei-kang, and Wang Chao. Rediscussion about angular glint of the extended target[J].Systems Engineering and Electronics, 2007, 29(4): 499-504.

[3]Lindsay and James E. Angular glint and the moving, rotating,complex radar target[J].IEEE Transactions on Aerospace and Electronic Systems, 1968, 4(2): 164-173.

[4]李小龙, 王星, 程嗣怡, 等. 基于MIMO雷达技术的导引头角闪烁抑制技术研究[J]. 弹箭与制导学报, 2011, 31(2): 57-59.

Li Xiao-long, Wang Xing, Cheng Si-yi,et al.. The study on seeker angular glint suppressing technology[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(2):57-59.

[5]王克让, 贺亚鹏, 柏磊, 等. 基于微动散射点分离的角闪烁抑制方法[J]. 南京理工大学学报, 2012, 36(4): 690-695.

Wang Ke-rang, He Ya-peng, Bai Lei,et al.. Angle glint suppression based in micor-motion dynamics scatters separation[J].Journal of Nanjing University of Science and Technology, 2012, 36(4): 690-695.

[6]Rius J M and Jofre L. High-frequency RCS of radar targets in real time[J].IEEE Transactions on Antennas and Propagation, 1993, 41(9): 1308-1319.

[7]Rius J M, Ferrando M, and Jofre L. GRECO: graphical electromagnetic computing for RCS prediction in real time[J].IEEE Antennas and Propagation Magazine, 1993, 35(2):7-17.

[8]刘立国, 张国军, 莫锦军, 等. 基于图形电磁学的雷达散射截面计算方法改进[J]. 电波科学学报, 2012, 27(6): 1146-1151.

Liu Li-guo, Zhang Guo-jun, Mo Jin-jun,et al.. Improvement of graphical electromagnetic computing method for radar cross section[J].Chinese Journal of Radio Science, 2012,27(6): 1146-1151.

[9]徐晓飞, 曹祥玉, 高军, 等. 基于矩量法的电大目标RCS核外并行计算[J]. 电子与信息学报, 2011, 33(3): 758-762.

Xu Xiao-fei, Cao Xiang-yu, Gao Jun,et al.. Parallel out-ofcore calculation of electrically large objects' RCS based on MOM[J].Journal of Electronics&Information Technology,2011, 33(3): 758-762.

[10]赵克明, 孙玉发. 一种应用于目标宽带 RCS快速计算的高效预处理技术[J]. 电子与信息学报, 2011, 33(4): 992-996.

Zhao Ke-ming and Sun Yu-fa. A high efficient preconditioning technique applied to the fast calculation of wide-band RCS of objects[J].Journal of Electronics&Information Technology, 2011, 33(4): 992-996.

[11]方宁, 宁焕生, 王宝发. 复杂目标可视化角闪烁偏差计算[J].北京航空航天大学学报, 2006, 32(2): 186-189.

Fang Ning, Ning Huan-sheng, and Wang Bao-fa. Visual computation of glint error for complex targets[J].Journal of Beijing University of Aeronautics and Astronautics, 2006,32(2): 186-189.

[12]方宁, 王谷, 王宝发. 复杂涂覆目标的角闪烁特性分析[J]. 北京航空航天大学学报, 2011, 37(3): 259-262.

Fang Ning, Wang Gu, and Wang Bao-fa. Analysis of glint characters of complex coated target[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(3):259-262.

[13]周剑雄. 光学区雷达目标三维散射中心重构理论与技术[D].[博士论文], 国防科学技术大学, 2006.

[14]范红旗, 王胜, 祝依龙, 等. 相位梯度法计算近场角闪烁的解析式[J]. 电子学报, 2009, 37(5): 937-941.

Fan Hong-qi, Wang Sheng, Zhu Yi-long,et al.. An analytic expression for computing near field angular glint by phase gradient method[J].Acta Electronica Sinica, 2009, 37(5):937-941.

[15]祝依龙, 范红旗, 付强, 等. 雷达目标特征信号与运动模式的相关性研究[J]. 中国科学: 信息科学, 2012, 42(7): 907-922.

Zhu Yi-long, Fan Hong-qi, Fu Qiang,et al.. Relationship between radar target signatures and motion modes[J].Scientia Sinica Informationis, 2012, 42(7): 907-922.

[16]Xia Ying-qing, Tian Hua-mei, Duan Zhi-guo,et al.. Research on the angular glint of targets in the near-zone[J].Wuhan University Journal of Natural Sciense, 2007, 12(3): 481-484.

[17]殷红成, 邓书辉, 阮颖铮, 等. 利用后向散射回波相对相位计算角闪烁的条件[J]. 电子学报, 1996, 24(9): 36-39.

Yin Hong-cheng, Deng Shu-hui, Ruan Ying-zheng,et al.. On the conditions for obtaining angular glint by backscattering echo relative phase[J].Acta Electronica Sinica, 1996, 24(9):36-39.