基于核范数凸优化的微阵列缺失点重建

孟繁驰，李书琴，蔡 骋

(西北农林科技大学信息工程学院，陕西杨凌712100)

0 引言

基因微阵列技术在生物实验中已经得到了广泛的应用，从微阵列得到的基因表达值，通常以大规模矩阵的形式呈现［1］。由于微阵列实验中各种因素的影响，如杂交失败、图像的噪声、污染等，从微阵列得到的基因矩阵通常含有缺失点［2］。然而，基因下游的实验，如常用的分类、聚簇方法等，通常需要完整的矩阵作为输入。鉴于此，不同类型的基因微阵列缺失点的重建方法陆续产生。目前常用的基因微阵列缺失点的重建方法包括奇异值分解SVD［3］、K最近邻KNN［3］、贝叶斯主成分分析BPCA［4］、最小二乘法LSimpute［5］、局部最小二乘法 LLSimpute［6］等。在以上各种方法中，LLSimpute被实验证明可以在各种类型的基因数据集上取得较高的重建精确度［1，6-8］。

1 LLSimpute方法

LLSimpute是Hyunsoo Kim等人在2005年提出的方法［6］。该方法利用基因与基因之间的线性关系来重建目标基因中的缺失点。以一个m×n的基因微阵列矩阵为例，简要介绍一下LLSimpute的流程:

(1)从其他m-1个基因行中找出与目标基因 (即当前需要重建的含缺失点的一行基因)g1距离最近的k个基因，组成列向量 (g1，gs1，…，gsk)T。

(2)找出目标基因中的缺失点g1×q和非缺失点g1×(n-q)。其中q表示该行中有q个缺失点。

(3)将缺失的点g1×q组成的向量表示为α，将非缺失的点g1×(n-q)组成的向量表示为wT。从gs1到gsk中找出与g1中的缺失点对应的列上的基因，组成矩阵 (或向量)Bk×q，从gs1到gsk中找出与g1中的非缺失点对应的列上的基因，组成矩阵Ak×(n-q)。假设目标基因上有两个缺失点，则形成的矩阵如式 (1)所示

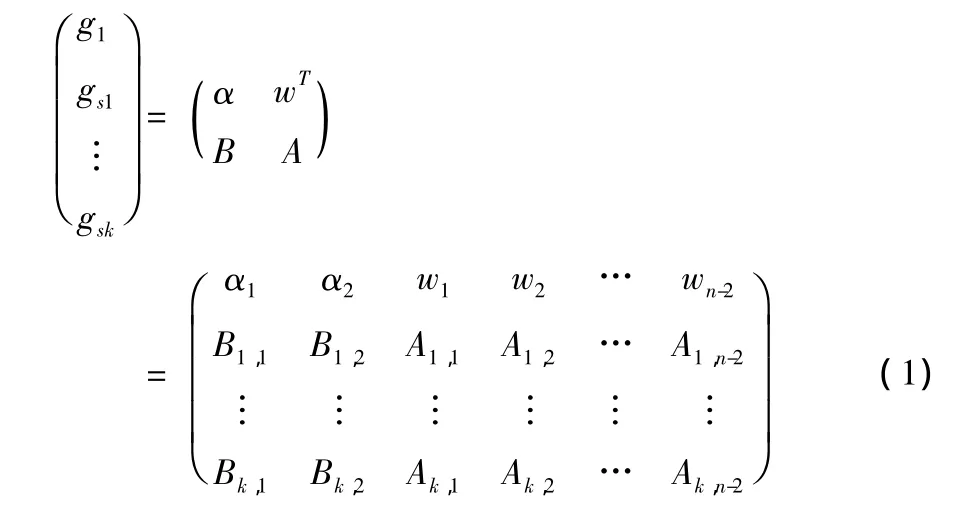
(4)在以上矩阵中，wT、B、A是已知的，α表示目标基因中待重建的缺失点组成的向量。由wT和A之间的线性关系，求系数向量x，可以看作一个最小二乘法问题 (2)

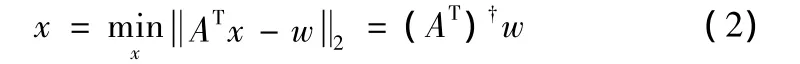
其中(AT)是AT的伪逆阵 (Pseudoinverse)。从而

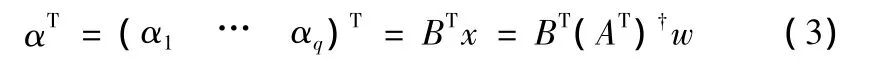
实验表明，在k选择合适的时候，LLSimpute可以获得非常好的重建效果。［6］中，为了找出最优的k值，作者采取了如下的方法:首先，用每行的均值将该行中的缺失点填充，得到一个完整的矩阵。然后在该完整的矩阵当中人为地去掉一些点，构成一个人造的含缺失点的矩阵。用不同数量的k个邻居，使用LLSimpute去重建，得到重建出的缺失点的数值。由于这些缺失点是人为制造的，所以它们的真实值是已知的，这样，不同k对应的重建错误率是可以计算的。最后，取对应重建错误率最低的k，在基因微阵列矩阵中作为选取的邻居数。

2 矩阵填充

矩阵填充 (matrix completion，MC)是 Candès等人在2009年提出的方法 ［9］。在 ［9］中，作者证明了一个含有缺失点的矩阵，在低秩的情况下，如果其中所含的非缺失点足够多，则完整的矩阵是可以在一定的概率下恢复出来的。因此，矩阵填充可以认为是一个 (4)所示的优化问题

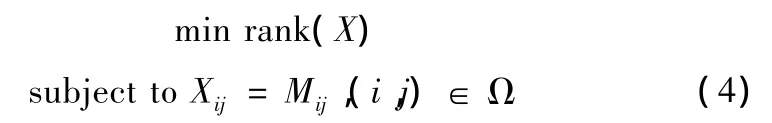
其中M是观测到的，含有缺失点的矩阵，Ω是非缺失点的元素对应的下标组成的集合，X是待重建的完整矩阵。但 (4)是一个NP难问题。然而矩阵X的秩与矩阵X的奇异值中非零元素的个数是一样的，所以［9］中，X的秩被X的核范数 (nuclear norm)所代替，上式变为 (5)所示的优化问题

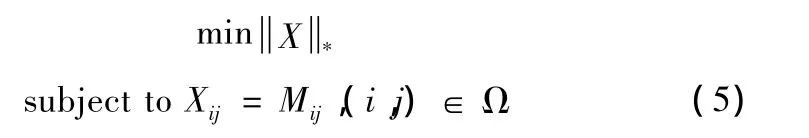
其中‖·‖*表示核范数，等于所有奇异值的和。式(4)和式 (5)的区别在于，式 (4)中X的秩对应的是其奇异值组成的向量的0范数，而式 (5)中X的核范数对应其奇异值组成的向量的1范数。式 (5)所对应的优化问题是凸的，具有唯一的解。

矩阵填充已经被成功用在Netflix视频推荐系统［10］、视频去噪上［11］。林宙辰等人提出的非精确增广拉格朗日乘子(inexact augmented lagrange multiplier，IALM)［12］是解决式(5)所示的优化问题的一个有效方法，在重建精确度和运行速度上均占有很大优势。

IALM采用拉格朗日乘子解决 (5)所示的核范数凸优化问题，这里，矩阵填充问题被描述为式 (6)所示的一个优化问题

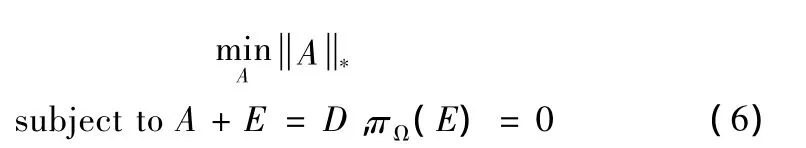
式中:A——待重建的矩阵，D——观测到的有缺失点的矩阵，πΩ——一个的线性变换。IALM在每次迭代中求奇异值分解，每次取较大的几个奇异值来重建矩阵A和E，从而使A趋向于低秩。详细的迭代过程，可参考［12］。本文中，将使用IALM进行矩阵填充，得到完整基因微阵列矩阵的方法称为MC方法。该方法和其他方法的对比实验结果将在第4章中给出。

3 矩阵填充对LLSimpute的改进

由LLSimpute中的第1步可以看出来，与目标基因对应的k最近邻基因行必须是完整的，才可以构成式中的A矩阵和B矩阵。同样，在自适应地寻找最优的k时，也需要完整的矩阵。然而实际的基因微阵列矩阵往往是多行都含有缺失点。一种解决办法是在找k最近邻的时候，忽略掉含有缺失点的基因，只在完整的基因中寻找邻居，这种办法在缺失率比较低的时候是可行的，但是当缺失率较高时，大多数基因都是不完整的，按照这个方法，会带来邻居数量过少的问题。实验也表明，LLSimpute对k选取是非常敏感的，若只在完整的行中寻找邻居，在缺失率大于等于5%的时候，LLSimpute就会因可选取的邻居数量过少，而使重建错误率大大升高。

由此可以看出，LLSimpute需要一个事先填充好的“中间矩阵”才可以构造A矩阵和B矩阵，以及寻找最优的k。对于这个“中间矩阵”，文献［6］中采用行均值的方法得到，即在含缺失点的矩阵当中，用每行的均值来代替缺失点，得到完整的矩阵。在本文的第2章中，已经提到了用矩阵填充得到完整矩阵的方法。矩阵填充得到的结果，可以作为最终重建后的微阵列矩阵，也可以作为一个“中间矩阵”，继续使用LLSimpute来进行重建。这样，即将LLSimpute中的行均值填充的过程，替换为矩阵填充的过程。在本文中，将这种改进的LLSimpute称为MC_LLS方法。

用行均值填充可以构成一个完整的矩阵，但行均值只利用了每个目标基因本行的信息。MC_LLS方法中的MC过程是以矩阵的低秩为优化目标，利用的是矩阵的全局特性，而LLSimpute本身，是基于矩阵的局部特征的，所以MC_LLS方法，实际上同时利用了矩阵的全局特征和局部特征。MC_LLS方法的实验结果，也将在第4章中给出。

4 实验与结果

对目前常用的几种方法 (KNN、BPCA、LLSimpute)，和本文提出的MC、MC_LLS方法进行对比试验，并给出结果的分析。

4.1 数据集

试验在4个公开的真实基因微阵列数据集上进行。前两个数据都属于时间序列。其中第一个数据集来自［13］中的酵母细胞的CDC15序列和CDC28序列，将其称为CDC15_28。第二个来自 ［13］中的酵母细胞的alpha序列，称为SP_APLHA。第三个数据集来自文献［14］中的人类癌细胞株，是一个非时间序列，称为NCI60。第四个数据集来自［15］中的淋巴瘤细胞，也是一个非时间序列，称为lymphoma。其中CDC15_28在综述［1］中也被用于对各种方法进行比较，SP_APLHA在 ［6］中被用于检验LLSimpute的重建精确度，NCI60与综述［1］中的NTS来自相同的细胞株，lymphoma在LSimpute［5］中也被采用。各个数据集的总行列数、完整的行列数 (即除去含缺失点的行之后的大小)以及类型可见表1。

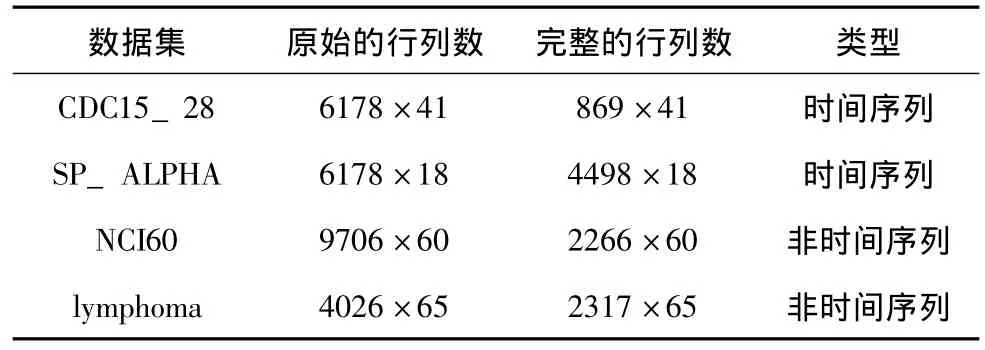
表1 实验采用的数据集

这些数据集原本都是不完整的，为了评价重建后的错误率，需要完整的微阵列矩阵作为参考。为此，将矩阵中不完整的行去掉，只保留完整的行 (如表1中的第三列)。再在这些完整的行中按不同的比例随机去除一些已知点，作为缺失点。同样的方法也在 ［1，6］中被采用。这样，可以同时得到完整的微阵列矩阵和它们对应的不同缺失率下的缺失矩阵。对不同缺失率的矩阵进行重建，将重建后的矩阵和完整的矩阵对比，可以得出重建误差。

4.2 参数选择

对于KNN方法，在CDC15_28和SP_ALPHA数据集上，邻居数k值设为10;在NCI60和lymphoma数据集上，k设为5，这两个k值处于KNN最优的参数范围区间内［1］。BPCA的参数设为其默认值，即微阵列矩阵的列数减去1。LLSimpute中的参数k使用 ［6］中模拟缺失点筛选k的方法得到的值。MC_LLS中的k也采用模拟缺失点的方法得到。需要说明的是，对于LLSimpute和MC_LLS，在寻找邻居时，若缺失率足够低 (此时完整的行数相对比较多)，则只从完整的基因行中寻找，而不是从用行均值或MC填充好的“中间矩阵”中寻找，以有效利用矩阵本身的真实值。

4.3 重建评价标准

目前对于基因重建效果的评价，多采用的是标准化根均方差 (normalized root mean squared error)［1，4，6］，称为NRMSE，定义如下

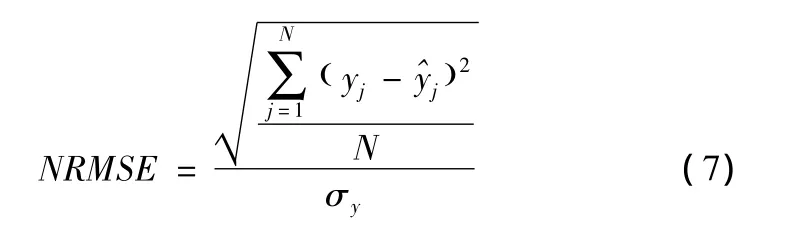
式中:yj——基因第j位上原始的值，j——该位置上重建后的值，N——要重建的基因点的总数，即缺失点的个数，σy——N个原始基因点的标准差 (standard deviation)。NRMSE值越低，表明重建错误率越低。

4.4 重建结果

对4.1中的4个数据集，按照从1%到25%的之间的8种不同的缺失率，构造缺失点。对于每种数据集，不同缺失率下的重建都进行10次重复实验，取10次标准化根均方差的平均值作为最终的重建错误率。图1—图4分别给出了不同方法在CDC15_28、SP_ALPHA、NCI60和lymphoma数据集上的结果。

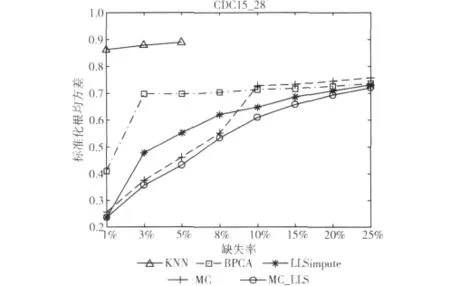
图1 在数据集CDC15_28上的重建错误率

图1中，KNN的曲线在较高的缺失率下被截断，表示在这些错误率下，基因的每行都存在缺失点，从而无法从完整的行中找到最近邻。在缺失率小于10%的情况下，MC的重建错误率明显低于KNN、BPCA和LLSimpute。但是随着缺失率的升高，MC的错误率也开始变大。然而MC_LLS表现很稳定，在任何缺失率下，重建错误率都是最低的。

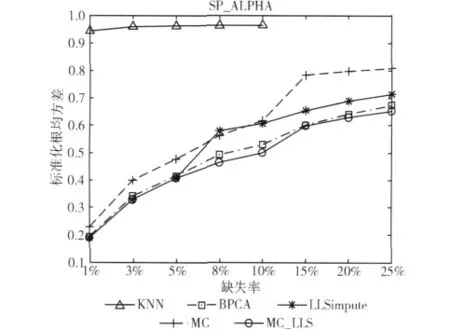
图2 在数据集SP_ALPHA上的重建错误率

由图2可以看出，在数据集SP_ALPHA下，KNN的表现仍然是最差的，重建错误率始终高于0.9。LLSimpute在缺失率较低的情况下有较低的错误率，但当缺失率大于5%时，错误率明显提高。MC在缺失率为8%的时候，错误率小于LLSimpute，在其他缺失率下均高于LLSimpute、BPCA和MC_LLS。但是总体上，仍然是MC_LLS取得了最低的重建错误率。

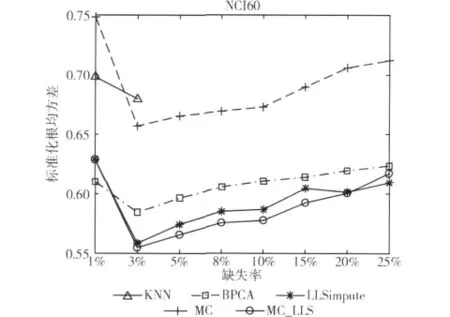
图3 在数据集NCI60上的重建错误率

NCI60数据集是一个非时间序列，具有很强的局部相关性，所以图3中基于数据全局特征的BPCA和MC在这里的重建错误率明显比LLS、MC_LLS高出很多。而基于局部相关性的KNN，在这里的表现虽然仍然比较差，但是已经取得了比时间序列下更低的错误率。对于MC_LLS，在大多数的缺失率下，仍然具有最低的重建错误率。

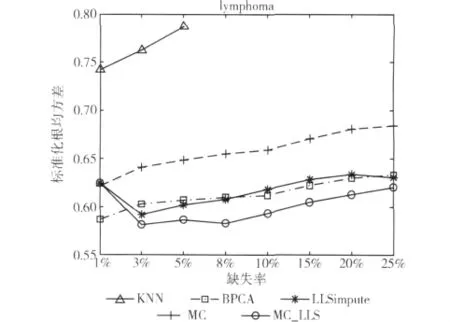
图4 在数据集lymphoma上的重建错误率

与数据集NCI60类似，图4中的数据集lymphoma也具有较强的局部相关性。LLSimpute和BPCA的表现非常接近，KNN的结果仍然是最差的。虽然MC本身的NRMSE高出LLSimpute和BPCA，但MC_LLS仍然在除1%之外的其他所有缺失率下取得了最低的重建错误率。

由以上实验结果可以得出结论，基于矩阵全局特征的MC方法在局部相关性较弱的数据集上具有优势，但是不适用于局部相关性很强的数据集。而MC_LLS由于结合了矩阵的整体相关性和局部相关性，所以在任何类型的数据集上都表现出了最好的重建结果。

表2所示的是各种方法在CDC15_28数据集上，不同缺失率下的运算时间，单位是秒。每个时间都是在进行了10次重复实验后求得的平均值。实验在一台装有4核Intel Xeon E5504 2.0GHz处理器的计算机上进行，采用Matlab R2011a。

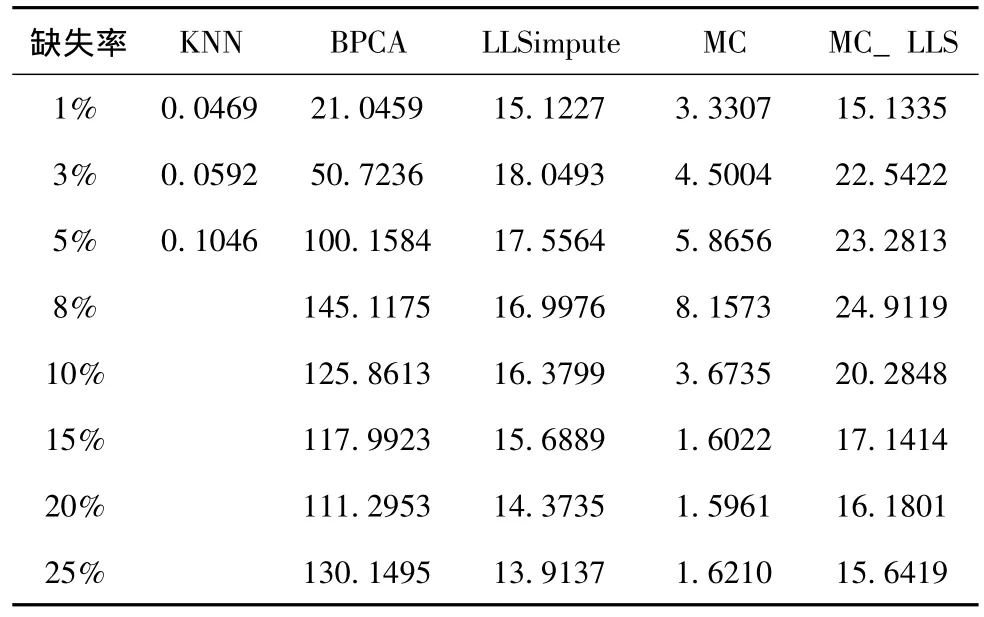
表2 各种方法在数据集CDC15_28上的运算时间 (秒)

虽然矩阵填充中的奇异值分解通常是一项比较耗时的计算，但由于IALM使用了部分奇异值分解［12］，所需时间大大减少，所以MC方法在运算时间上具有明显的优势。而相对于LLSimpute，MC_LLS在时间开销增加不明显的情况下，却明显降低了重建错误率。

5 结束语

使用非精确增广拉格朗日乘子 (IALM)解决了矩阵填充 (MC)问题，实现了基因微阵列矩阵的核范数凸优化。含有缺失点的微阵列矩阵，在进行矩阵填充后，可以作为最终的重建结果，并且矩阵填充得到的结果作为中间矩阵，还可以替换LLSimpute中的行均值矩阵。在四个常用的基因微阵列数据集上的实验结果表明矩阵填充方法 (MC)在某些时间序列微阵列矩阵的部分缺失率下可以取得比KNN、LLSimpute和BPCA更高的重建精确度，并且计算时间具有明显优势。矩阵填充和LLSimpute结合的方法 (MC_LLS)，在实验的四个数据集中的几乎所有缺失率下，取得了最高的重建精确度，并且相对LLSimpute时间增加不明显。

［1］Bras L P，Menezes J C.Dealing with gene expression missing data［J］.Syst Biol(Stevenage)，2006，153(3):105-19.

［2］Liew Alan Wee-Chung，Law Ngai-Fong，Yan Hong.Missing value imputation for gene expression data:Computational techniques to recover missing data from available information［J］.Briefings in Bioinformatics，2011，12(5):498-513.

［3］Troyanskaya Olga，Cantor Michael，Sherlock Gavin，et al.Missing value estimation methods for DNA microarrays［J］.Bioinformatics，2001，17(6):520.

［4］Oba Shigeyuki，Sato Masa-aki，Takemasa Ichiro，et al.A bayesian missing value estimation method for gene expression profile data［J］.Bioinformatics，2003，19(16):2088.

［5］B Trond Hellen，Dysvik Bjarte，Jonassen Inge.LSimpute:Accurate estimation of missing values in microarray data with least squares methods［J］.Nucleic Acids Research，2004，32(3):e34.

［6］Kim Hyunsoo，Golub Gene H，Park Haesun.Missing value estimation for DNA microarray gene expression data:Local least squares imputation［J］.Bioinformatics，2005，21(2):187.

［7］Brock Guy N，Shaffer John R，Blakesley Richard E，et al.Which missing value imputation method to use in expression profiles:A comparative study and two selection schemes［J］.BMCbioinformatics，2008，9(1):12.

［8］Magalie C，Alain M，Ga lle L.Comparative analysis of missing value imputation methods to improve clustering and interpretation of microarray experiments［J］.BMCgenomics，2010，11(1):15.

［9］Candès Emmanuel J，Recht Benjamin.Exact matrix completion via convex optimization［J］.Foundations of Computational Mathematics，2009，9(6):717-772.

［10］Bennett James，Lanning Stan.The netflix prize［R］.California，USA:KDDCup，2007.

［11］JI Hui，LIU Chaoqiang，SHEN Zuowei，et al.Robust video denoising using low rank matrix completion［C］//IEEE Conference on Computer Vision and Pattern Recognition，2010.

［12］LIN Zhouchen，CHEN Minming，MA Yi.The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices［J］.Arxiv preprint arXiv:1009.5055，2010.

［13］Spellman Paul T，Sherlock Gavin，ZHANG Michael Q，et al.Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization［J］.Molecular biology of the cell，1998，9(12):3273.

［14］Scherf Uwe，Ross Douglas T，Waltham Mark，et al.A gene expression database for the molecular pharmacology of cancer［J］.Nature genetics，2000，24(3):236-244.

［15］Alizadeh A Alizadeh，Eisen Michael B，Davis R.Eric，et al.Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling［J］.Nature，2000，403(6769):503-511.