“通性通法”教学重在“回归自然”——从两则教学案例谈起

☉浙江省象山县第二中学 吕增锋

所谓通性通法是指具有某种规律性和普遍意义的常规解题模式和常用的数学解题方法.在数学解题教学中要“淡化特殊技巧，注重通性通法”的观点也得到越来越多教师的共识.在这种教学观的指导下，学生不仅可以跳出“题海”，集中精力在理解数学的本质上下功夫，而且可以实现“练一题，学一法，会一类，通一片”的目的.但我们也看到由于很多教师对“通性通法”认知存在不足，因此在开展“通性通法”教学时难免出现偏差.

一、两则教学案例

案例1：已知f（2x+1）=x2－2x，求f（x）与f（2x－1）的解析式.

这是一堂关于函数表达式习题课，教学对象是高一学生.

生1解法：设f（x）=ax2+bx+c（a≠0），则

f（2x+1）=4ax2+（4a+2b）x+a+b+c=x2－2x.

易得4a=1，4a+2b=－2，a+b+c=0.

师：为什么可以“设（fx）=ax2+bx+c（a≠0）”？

生1：因为可以推测（fx）一定是二次函数，如果（fx）不是二次函数，则（f2x+1）的解析式也不会是二次函数.

师：你证明过你的推测吗？

生1：我想应该是的.

师：想的不一定都对，数学是严密的，要证明的.而且你这种方法过于烦琐，尽管答案是正确的，但我们不提倡.下面我介绍一下这道题目的标准解法.

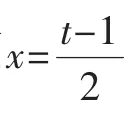
生2：为什么要设2x+1=t？求出的是（ft），为什么就变成了（fx）？

……

案例2：已知（fx）的定义域为R，当x＜0时，（fx）=x2+x－2.

（1）若（fx）是偶函数，求当x＞0，（fx）的解析式；

（2）若（fx）是奇函数，求（fx）的解析式.

这是一堂函数奇偶性的习题课，教学对象也是高一学生.教师出示问题后，让生3板演，其他学生在下面解答.

生3解法：先画出（fx）=x2+x－2（x＜0）的图像（如图1、图2所示），然后根据对称性再画出x＞0部分的图像，最后观察图像求出相应的解析式.

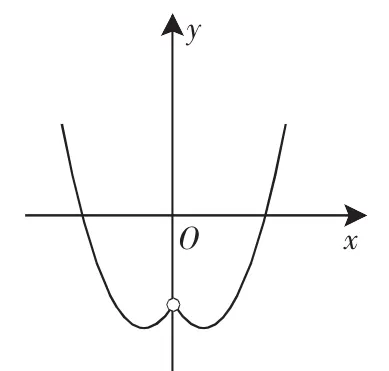
图1

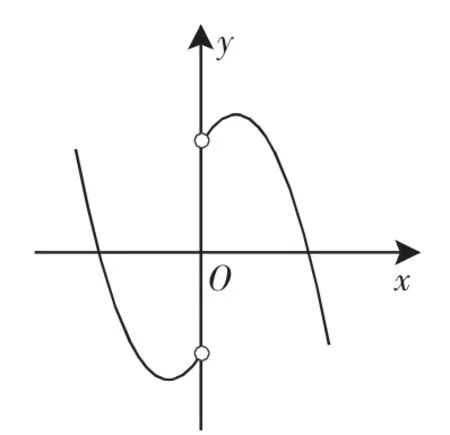
图2

教师发现几乎所有学生的都是采用先画图，再求解析式的方法，脸上露出了失望的神情.于是他让学生抬起头，集中注意力，听他讲解这类题目的标准解法.

师：我发现大家采用的都是先画图，后求解析式的方法解决这道题目的，但显然这种方法不够严密，并且有相当大的局限性.若求的是陌生函数的解析式，你能做出它的图像吗？

生3：不能.

师：下面我就为大家讲述这道题目的标准解法.

教师解法：（1）设x＞0，则－x＜0，所以f（－x）=（－x）2－x－2=x2－x－2.因为f（x）是偶函数，则f（x）=f（－x）=x2－x－2，所以f（x）=x2－x－2（x＞0）.

师：大家清楚了没有？

学生一脸茫然，不知所措，开始纷纷提出疑问.

生4：老师“设x＞0，则－x＜0”什么意思，为什么要这么做？

生5：怎么一会是f（x），一会是f（－x），搞不清楚.

……

以上两则通性通法的教学只能用“简单、粗暴”来形容.“简单”主要体现在教授通性通法时不注重方法，偷工减料，省去了必要的铺垫和引导；“粗暴”体现在教师无视学生的认知规律和原有的知识水平，强行推销所谓的通性通法置学生心理感受于不顾，使得通性通法的教学异化为对标准解法追逐.

二、急功近利，欲速不达

通性通法教学为何出现如此匪夷所思的现象呢？若深究其背后的原因，无非是教师在教学中追求速成，急功近利的心态使然.为了追求所谓的高效，让学生快速达到掌握标准解法的目的，教师对教学的处理是“精打细算”，能省则省.以上述二则案例为例，由于高一学生数学思维不够成熟，知识储备不够丰富，在解题中难免会走“弯路”，冒出教师眼中那种“不合时宜”的解法.而教师却没有耐心仔细审视学生的思路和解法，利用“简单而粗暴”的手段“快刀斩乱麻”，希望快速规范和强化高一学生的解题思路，从而使所谓的通性通法成为了学生唯一的选择.但事实上如此的速成之道严重阻碍了通性通法的教学，使得教学效果大打折扣.众所周知，数学教学不是一蹴而就的“经营模式”，而是一种长期的“经营策略”，数学教学是一种“潜移默化”，“螺旋上升”的过程.课堂不仅是教师传授知识的地方，还应该是激发学生的求知欲，展现学生自我风采的舞台.通过课堂中学生表现出的迷茫和疑惑，我们完全有理由断定教师这种“只重结果，不重过程”的短视行为根本无助于提升学生对通性通法的认同感，不仅使得通性通法在学生是眼里成了“怪法”，成了“天外来物”，而且严重抑制了学生数学思维的发展.

三、只见树木，不见森林

单纯从字面上看，通性通法无非是指解决具有相同性质数学问题所用的通用的思想方法.但在实际操作中，总结和发现数学中的通性通法其实并不是一件容易的事，很多教师经常会陷入“只见树木，不见森林”的尴尬境地.以上述二则教学案例为例，在教师眼里似乎只有两道题的解法属于通性通法的范畴，而根本没有认识到在教学过程中所展现的其他数学思想方法实际上也是通性通法，而它们的价值和地位有时却远远高于这两道题本身的解法.

在案例1中，其实我们不得不佩服学生的解题直觉，一看到f（2x+1）=x2－2x，马上联想已学过的几个函数，并且大胆的推测f（x）是二次函数，这正是合情推理思想在数学解题中的具体体现，这难道不是我们在整个高中阶段所倡导的通性通法吗？合情推理的实质是“发现——猜想”，在解决问题时的合情推理的特征是不按逻辑程序去思考，但实际上是学生把自己的经验与逻辑推理的方法有机地整合起来的一种跳跃性的表现形式.合情推理在高中阶段通常不会像演绎推理那样受到师生的重视，教师本可以借此唤醒学生对合情推理的认知，尽管学生在应用的过程中存在着“忽视严密”的瑕疵，但完全可以在教师的引导下证明猜想的正确性.但令人遗憾的是，教师完全无视学生的思维成果，抱守题目的标准解法，固步自封.

在案例2中，数学结合的思想是高中数学解题的最基本的思想之一，当然也是重要的通性通法之一.学生能够想到从图形入手，经过观察、分析等思维过程圆满解决问题对高一新生来说已是难能可贵，尽管这种思想方法存在着较大的局限性.作为教师首先应该对学生的解法给予高度的评价，强化学生思维中的数形结合的意识.

四、回归自然，螺旋上升

鉴于对通性通法的种种认知不足和教学偏差，那么我们应该如何把握通性通法的教学？

首先我们在通性通法的教学上应该回归自然.通性通法之所以称为通性通法是因为它常常从基本概念、原理出发，以基础知识为依托、以基本方法为技能，按照既定的步骤，逐步推出问题和解答，解法思想顺乎一般思维规律，其具体操作过程易于为多数学生所掌握.因此在教学中应注意讲清通法的概括过程，并通过启发和引导，向学生提示每种通法产生的过程，这样更有利于学生对通法本质，对数学思想的理解，从而使学生感到通性通法自然、流畅、易于理解、易于掌握和运用的.以案例2的问题为例，学生的解法确实有其局限性，教师的解法确实是学生应该掌握的通性通法，但这种方法涉及到了一些对高一新生来说很陌生的数学思想方法，如“设x＞0”，然后通过转换成“－x＜0”，代入已知解析式求出未知的解析式，这种设未知——变已知——代已知——求未知的解题思路实际上是化归思想一种具体表现，对刚刚接触函数不久的学生来说在理解上确实有很大的困难.这就需要教师加强引导，帮助学生理清解题思路，让学生感受到解题方法是自然合理的.比如，教师不妨把这种解题思路形象概括为“移花接木”法，这样就会有助于学生对解题思路的理解.

其次我们在通性通法的教学上要遵循螺旋上升原则.中学数学中常用的数学解题通性通法有换元法、配方法、待定系数法、参数法、消元法、特殊值法等，涉及的数学思想包括：转化思想、方程思想、数形结合思想、分类讨论思想、合情推理等.由此可见，通性通法涉及的内涵是既丰富又烦琐，因此我们在教学中切勿急功近利，而要遵循学生的认知规律，采取由易到难，由具体到抽象的策略.比如，高一学生刚刚开始接触数学，抽象思维相对薄弱，让学生形成从具体图形入手解决数学问题的思维习惯应该就是这个阶段最为重要的通性通法.然后通过学生思维的不断完善，数学视野的不断拓展，教师再引领学生探索更为抽象的数学思想方法，从而逐步摆脱具体图形的束缚，最终实现数与形的完美融合，领悟数形结合思想的精髓.又比如，求函数值域思想方法多达十余种，但其中学生容易掌握的最主要的通性通法就是利用函数的单调性求值域；在判断函数单调性的方法中，高一新生应该掌握的通性通法是利用单调性的定义直接判定；随着函数学习的不断深入，利用复合函数的性质判断函数单调性就成为了又一个需要学生掌握的通性通法；到了高二学生接触到导数的知识后，那么利用求导判定函数的单调性就成为了学生今后的主要通性通法.这就是我们数学教学中要遵循的螺旋上升策略.

日本教育家米山国藏认为：“成功的数学教学，应当是数学精神，思想方法深深地、永远地、铭刻在学生的头脑里，长久地活跃于他们日常的业务中，虽然那时数学的知识已经淡忘.”通过上述分析，通性通法教学只有回归自然，才能让学生铭记于心.

1.肖瑞元.教学岂能急功近利［J］.陕西教育，2011（6）：12.

2.苏翠林.“合情推理”应贯穿教材的始终［J］.新课程研究（基础教育），2012（3）：15.

3.齐威娜.对中学数学解题通法的研究［D］.长春：东北师范大学，2008.