机载干涉SAR运动补偿中地物目标定位误差的影响分析

李银伟*①② 韦立登① 向茂生①



机载干涉SAR运动补偿中地物目标定位误差的影响分析

李银伟韦立登向茂生

(中国科学院电子学研究所微波成像技术国家级重点实验室 北京 100190)(中国科学院大学 北京 100049)

在基于IMU/GPS测量数据的运动补偿方法中，IMU测量误差和地物目标定位误差导致不准确的相位补偿量，从而引入残余运动误差。该文针对机载干涉SAR运动补偿中地物目标定位误差的影响，建立了在斜视条件下由地物目标定位误差引入的残余运动误差的数学模型，分析了导致地物目标定位误差的系统采样延时误差、多普勒中心频率误差和参考DEM误差对残余运动误差的影响，重点讨论了参考DEM误差对干涉SAR图像质量、干涉相位和相干系数的影响。该文的讨论结果为机载高精度SAR和重轨干涉SAR数据处理中运动补偿精度提供了理论基础。

机载干涉SAR；地物目标定位误差；运动补偿；残余运动误差

1 引言

在机载SAR系统中，由于受到大气湍流和人为控制的影响，天线相位中心(Antenna Phase Center, APC)总是偏离理想的匀速直线运动状态，因此SAR成像时必须进行运动补偿。而对于高分辨率机载SAR和机载干涉SAR系统来说，高精度的运动补偿是必不可少的。现阶段，通常选用基于IMU/GPS (Inertial Measurement Unit, IMU/Global Positioning System, GPS)测量数据的运动补偿方法。但是，诸多缺陷的存在会造成运动补偿的不充分，即在完成运动补偿处理后仍然存在残余运动误差。

机载干涉SAR系统的残余运动误差主要来源于IMU测量误差和SAR系统的参数误差，这些非理想因素会导致SAR航迹测量误差和地物目标定位误差，进而导致运动补偿中不准确的相位补偿量，从而引入残余运动误差。Fornara等人推导出IMU测量误差所导致的APC沿雷达视线(Line Of Sight, LOS)方向的斜距误差，分析了线性和二次斜距误差对SAR成像质量的影响。文献[4]详细推导了IMU测量误差与APC定位误差之间的函数关系，给出了IMU测量误差导致的相位误差的具体计算方法，并分析了其对SAR图像质量的影响。文献[5-7]提出了3种残余运动估计算法对APC的测量误差进行估计和补偿。地物目标的定位主要由3个约束条件决定，即：(1)地物目标的斜距，由雷达系统采样延时给出；(2)地物目标处的多普勒中心频率，可结合天线初始安装角和载机姿态角计算得到或由雷达回波数据估计得到；(3)地物目标的高程，由运动补偿时的参考DEM(Digital Elevation Model)给出(平地假设是其特例)。因此，系统采样延时误差(斜距误差)、多普勒中心频率误差和参考DEM误差会影响地物目标定位精度，从而引入残余运动误差，进而造成运动补偿中不准确的相位补偿量。文献[8]研究了基于检校场的天线安装姿态误差的标定方法，从而实现对多普勒中心频率的校准。文献[8-11]在研究波束中心近似不成立的同时简单分析了地形起伏对运动补偿的影响，提出了结合外部DEM的基于子孔径的运动补偿算法。文献[12]建立了计算残余运动误差的模型，利用实际数据分析了残余运动误差在回波信号域和距离多普勒域中引入的相位误差。但是，这些文献没有综合性地定量分析地物目标定位误差在运动补偿中对干涉SAR图像质量、干涉相位和相干系数的影响。

针对上述问题，本文对系统采样延时误差、多普勒中心频率误差和参考DEM误差所引入的残余运动误差进行了系统分析，基于参考文献[8]重点讨论了高程误差引入的残余运动误差对机载干涉SAR成像质量、干涉相位和相干系数的影响，为机载高精度SAR和机载重轨干涉SAR数据处理中运动补偿精度提供了理论基础。本文的内容安排如下：第1节简单介绍了残余运动误差的来源和研究现状，明确了本文的研究范畴；第2节对地物目标定位误差引入的残余运动误差进行建模，分析了系统采样延时误差、多普勒中心频率误差和参考DEM误差对残余运动误差的影响；第3节重点分析了参考DEM误差引入的残余运动误差对干涉SAR图像质量、干涉相位和相干系数的影响；最后对本文内容进行了总结概括。

2 地物目标定位误差引入的残余运动误差

图1为基于IMU/GPS测量数据的机载SAR系统运动补偿几何关系图，其波束中心斜视角为。

图1 基于IMU/GPS测量数据的机载SAR系统运动补偿几何关系图

(1)

运动补偿后雷达信号中残余的运动误差为：

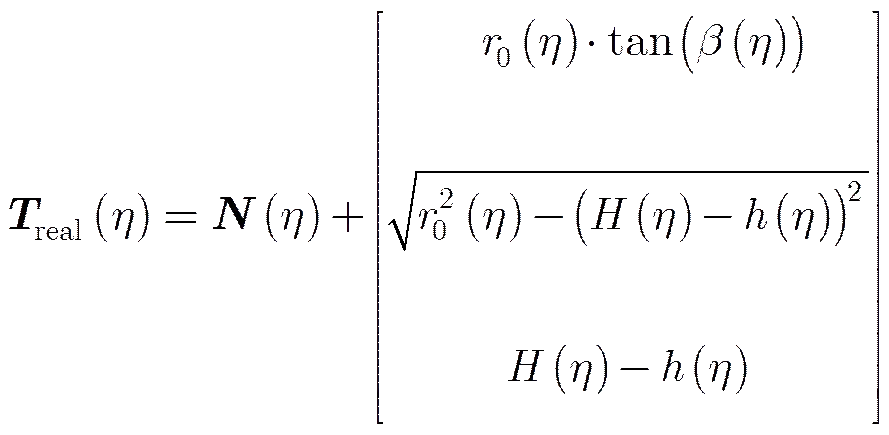
(7)

把式(4)-式(7)代入式(3)化简得：

(8)

式(8)表示由斜距误差、多普勒中心频率误差和高程误差等地物目标定位误差引入的残余运动误差。根据式(8)，分别给出斜距误差、多普勒中心频率误差和高程误差引入的残余运动误差随视角变化的情况，见图2。可以看到：与斜距误差本身相比，仅仅考虑斜距误差导致的地物目标定位误差引入的残余运动误差时，其引入的残余运动误差是很小的，可以忽略不计；多普勒中心频率误差引入的残余运动误差随着视角的增大而增大，但其可以基于检校场对天线安装姿态误差进行标定，从而结合惯性测量系统测量的载机姿态实现对多普勒中心频率的精确计算；高程误差引入的残余运动误差随着视角的增大而减小，由于地形的起伏变化和外部DEM的精度不足，甚至没有外部DEM而直接采用平地假设，其导致的地物目标定位误差在三者之间最为复杂。接下来主要分析高程误差引入的残余运动误差对干涉SAR图像质量、干涉相位和相干系数的影响。

3 高程误差分析

忽略式(8)中斜距误差和多普勒中心频率误差，对其进行化简得：

3.1 高程误差对干涉SAR图像质量的影响

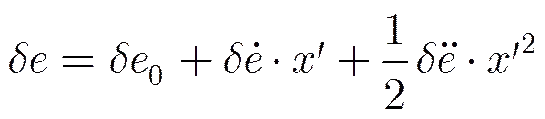
下面结合文献[8]，分3种情况对其进行讨论：

由图3(a)可知，方位向偏移在十米量级内，相比于方位向亚米级分辨率来说，这样的偏移将会使复图像由于方位向失配而显著去相干；同时由于斜视角的存在，相位误差急剧增大。例如，对于的高程误差坡度，在斜视角分别为和的情况下，相位误差分别为0.0019 rad和1.0872 rad，两者相差500多倍。

此线性残余误差与情况(1)一样不仅将会造成图像定位偏移，而且会产生相位误差。当常数高程误差m时，图4分别给出了不同斜距情况下图像方位向定位偏移和相位误差随着轨迹偏移线性系数的变化曲线。

同情况(1)一样，线性残余误差不仅会导致复图像由于方位向失配而去相干，而且会产生相位误差。例如，对于10 m的恒定高程误差，每百米的轨迹偏移不超过3.2 m时，相位误差将限定于以内。

图2 地物目标定位误差引入的残余运动误差 (中心频率fc=620 MHz，载机高度H=7 km，载机速度v=140 m/s，目标实际高程h=100 m，真实斜视角，轨迹偏移d=10 m，轨迹偏移夹角)

图3 方位向偏移和相位误差随着高程误差坡度的变化

由文献[1]知，此二次残余误差将会影响图像方位向聚焦，同时在点目标脉冲响应的最大幅度处将额外产生相位误差。其对图像方位向散焦的影响可以用式(11)来表示：

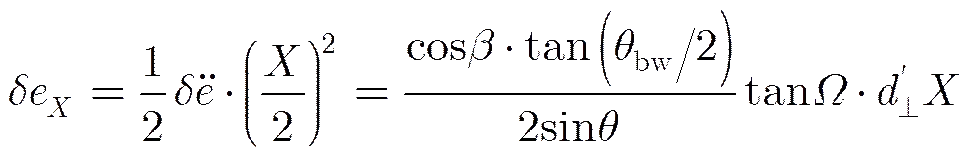
图4 方位向偏移和相位误差随着轨迹偏移线性系数的变化

Fig. 4 Variation of the azimuth deviation and the phase error for the different linear coefficient of the trajectory deviations

图5 不同波束宽度下的高程误差坡度和 合成孔径长度内的轨迹偏移

图6 图像方位向IRW展宽小于2%时的相位误差

3.2 高程误差对干涉SAR干涉相位的影响

在重轨干涉SAR中，主副图像的回波数据不是同时获取的。正如上部分所描述的那样，由于两次轨迹偏移的不同，高程误差引入的残余运动误差不仅使主副图像产生不同程度的散焦，而且引入不同的相位误差。这在干涉纹图生成过程中产生干涉相位误差。假设主副图像的残余运动误差分别为：

则其在最大幅度响应点处的相位误差分别为：

(13)

因此，干涉纹图中干涉相位误差为：

式(15)中方括号的第1项直接对应于斜距误差产生的干涉相位误差，其虽然类似于IMU测量误差，但在残余运动误差估计和补偿时，都假设只剩下IMU测量误差，这样将导致估计的IMU测量误差不准确；后两项则是在成像处理过程中产生的干涉相位误差项，其没有算法进行估计和补偿。当斜视角为时，残余运动误差线性项引入的干涉相位误差为，其最大值不超过主副图像中的最大相位误差。当斜视角非时，残余运动误差的线性项和2次项引入的干涉相位误差为：

其最大值为主副图像中相位误差绝对值之和。通常在利用MS算法进行时变基线估计时，基线精度要达到毫米级精度，这使得由于其它因素引入的干涉相位误差不能超过0.026 rad(1 mm斜距误差对应的相位)，因此在轨迹偏移确定的时候，必须选择对应精度的外部DEM来进行补偿。

3.3 高程误差对干涉SAR相干系数的影响

在干涉SAR系统中，衡量干涉纹图质量的参数是相干系数，因此接下来分析高程误差引入的残余运动误差对相干系数的影响。文献[8]给出了忽略基线去相干、噪声去相干等因素，只考虑存在斜距误差时相干系数的计算公式：

图7分别给出了3种情况下的相干系数变化图，其中细线和粗线分别代表波束宽度为和的相干系数。由图可知：斜距越小，高程误差导致的去相干越严重；线性误差尤其是图像方位向定位偏移越大时导致的去相干越严重。由图3 (a)中距离向偏移和方位向偏移公式知距离向偏移远小于方位向偏移，因此方位向失配是3.1节中情况(1)，情况(2)下最主要的去相关因素，它可能造成双通道图像的完全去相关。由方位向偏移公式可知此失配量不随方位向变化，而随距离向线性变化，易于通过图像配准处理消除其影响，但是线性误差造成的干涉相位误差需要通过其它方法消除。

图7 3种情况下的相干系数变化曲线

4 结论

本文针对机载干涉SAR运动补偿中地物目标定位误差的影响，对导致地物目标定位误差的系统采样延时误差、多普勒中心频率误差和参考DEM误差所引入的残余运动误差在斜视条件下进行数学建模，重点讨论了参考DEM误差对机载干涉SAR图像质量、干涉相位和相干系数的影响。地物目标定位误差引入的残余运动误差主要导致干涉SAR图像偏移、方位向散焦、干涉相位误差及去相干，其中线性残余运动误差引入的方位向失配是去相干的主要因素，但其易于通过图像配准消除。而残余运动误差引入的干涉相位误差不仅没有方法消除，而且其对时变基线估计造成影响，因此必须在轨迹偏移确定的情况下选择相应精度的外部DEM减小干涉相位误差，从而提高时变基线估计精度和DEM反演精度。

[1] Fornaro G. Trajectory deviations in airborne SAR: analysis and compensation[J]., 1999, 35(3): 997-1009.

[2] Mallorqui J J, Rosado I, and Bara M. Interferometric calibration for DEM enhancing and system characterization in single pass SAR interferometry[C]. IEEE Geosciences and Remote Sensing Symposium, Sydney, Australia, 2001: 404-406.

[3] Fornaro G, Franceschetti G, and Perna S. Motion compensation errors: effects on the accuracy of airborne SAR images[J]., 2005, 41(4): 1338-1352.

[4] Mao Yongfei, Xiang Maosheng, Wei Lideng,.. The effect of IMU inaccuracies on airborne SAR imaging[J].(), 2011, 28(4-6): 409-418.

[5] Reigber A, Prats P, and Mallorqui J. Refined estimation of time-varying baseline errors in airborne SAR interferometry[J]., 2006, 3(1): 145-149.

[6] Macedo K A C de, Scheiber R, and Moreira A. An autofocus approach for residual motion errors with application to airborne repeat-pass SAR interferometry[J]., 2008, 46(10): 3151-3162.

[7] Zhong Xuelian, Guo Huadong, Xiang Maosheng.. Residual motion estimation with point targets and its application to airborne repeat-pass SAR interferometry[J]., 2012, 33(2): 762-780.

[8] 唐晓青. 机载干涉SAR运动误差影响与补偿方法研究[D]. [博士论文], 中国科学院电子学研究所, 2009.

Tang Xiao-qing. Study on modeling and compensation for the influence of motion errors in airborne interferometric SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2009.

[9] Prats P, Reigber A, and Mallorqui J. Topography-dependent motion compensation for repeat-pass interferometric SAR systems[J]., 2005, 2(2): 206-210.

[10] Macedo K A C de and Scheiber R. Precise Topography- and Aperture-Dependent motion compensation for airborne SAR[J]., 2005, 2(2): 172-176.

[11] Zheng X, Yu W, and Li Z. A novel algorithm for wide beam SAR motion compensation based on frequency division[C]. Proceedings IGARSS’06, Denver, CO, July 31-Aug. 4, 2006: 3160-3163.

[12] Mao Yongfei, Xiang Maosheng, Wei Lideng,.. Error analysis of SAR motion compensation[C]. 2012 IEEE International Conference on Imaging Systems and Techniques, Manchester, United Kingdom, July 16-July 17, 2012: 377-380.

Effects of Target Positioning Error on Motion Compensation forAirborne Interferometric SAR

Li Yin-weiWei Li-dengXiang Mao-sheng

(National Key Laboratory of Science and Technology on Microwave Imaging, Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)(University of Chinese Academy of Sciences, Beijing 100049, China)

The measurement inaccuracies of Inertial Measurement Unit/Global Positioning System (IMU/GPS) as well as the positioning error of the target may contribute to the residual uncompensated motion errors in the MOtion COmpensation (MOCO) approach. Aiming at the effects of target positioning error on MOCO for airborne interferometric SAR, the paper deduces a mathematical model of the residual motion error caused by the target positioning error under the condition of squint. Also, the effects of the system sampling delay, Doppler center frequency, and reference DEM errors on the residual motion error that result in target positioning error based on the model are analyzed. Then, the paper discusses the effects of the reference DEM error on the interferometric SAR image quality, the interferometric phase, and the coherent coefficient. The research provides theoretical basis for the MOCO precision in signal processing of the airborne high precision and airborne repeat-pass interferometric SARs.

Airborne interferometric SAR; Target positioning error; MOtion COmpensation (MOCO); Residual motion error

TN959.3

A

2095-283X(2013)04-0492-07

10.3724/SP.J.1300.2013.13040

2013-04-09收到，2013-08-17改回；2013-08-28网络优先出版

国家973计划项目(2009CB724003)资助课题

李银伟 liyinwei19@163.com

李银伟(1985-)，男，河南扶沟人，2009年获得电子科技大学学士学位，现为中国科学院电子学研究所在读博士研究生，研究方向为SAR成像、运动补偿、干涉SAR信号处理。

E-mail: liyinwei19@163.com

韦立登(1973-)，男，中国科学院电子学研究所副研究员，硕士生导师，研究方向为干涉SAR数据处理技术。

E-mail: wld@mail.ie.ac.cn

向茂生(1964-)，男，中国科学院电子学研究所研究员，博士生导师，研究方向为干涉合成孔径雷达系统技术和方法。

E-mail: xms@mail.ie.ac.cn