北斗系统高轨卫星高精度定位模型病态性分析及改进方法

王胜利，王 庆，聂文锋，潘树国

（1.东南大学 仪器科学与工程学院，南京 210096；2.东南大学 交通学院，南京 210096；3.安徽理工大学 测绘学院，安徽 淮南 232001）

1 引言

北斗卫星导航系统 （BeiDou navigation satellite system，BDS）是全球卫星导航系统 （global navigation satellite system，GNSS）的重要组成部分［1］。BDS的导航星座主要由中圆地球轨道（medium earth orbits，MEO）卫星、地球静止轨道 （geostationary earth orbits，GEO）卫星及倾斜地 球 同 步 轨 道 （inclined geo－synchronous orbits，IGSO）卫星组成［2］，其中高轨道卫星GEO/IGSO运行轨迹变化相对缓慢，GEO/IGSO卫星相对接收机运动的角速度变化并不显著，由此导致的模糊度解算观测方程的病态性是BDS高精度定位模型的核心问题。

准确和快速确定模糊度固定值有两个前提：一是要有较准确的模糊度浮点解，二是要有较好的模糊度搜索方法［3-4］。模糊度解算的处理流程是首先进行最小二乘 （least square，LS）估计模糊度浮点解，然后结合各种搜索模糊度的方法来确定整周模糊度，其中最具影响力的搜索方法有最小二 乘 降 相 关 分 解 法［5-6］（least－square ambiguity decorrelation adjustment，LAMBDA）和最小二乘 模 糊 度 搜 索 法［7-8］（least－squares ambiguity search technique，LSAST）等。对于准确快速确定模糊度浮点解，文献［3］利用双差模型的法方程有三个特征值接近于零，其他特征值远大于它们的特征，提出了基于奇异值分解的Tikhonov正则化解法，结果表明在分米级基线偏差时解算模糊度成功率较高，但是不适合于基线偏差较大的情况。文献［4］针对这个问题，提出了利用基线先验精度信息实时估计正则化参数的正则化算法，结果表明结合其提出的模糊度线性约束条件可提高模糊度解算效率和正确率。文献［9］则进一步利用文献［3］中特征值的特征，构造了双k岭估计的方法对模糊度浮点解精度进行了改善。但是这些算法一是针对以轨道运行速度较快的中轨道MEO卫星为基础的全球定位系统 （global positioning system，GPS）及格洛纳斯卫星导航系统 （global navigation satellite system，GLONASS），而BDS主要由高轨道卫星组成，GEO/IGSO卫星平均运行角速度仅为MEO卫星的2%及60%左右，因此运行特征存在一定差别，二是与常规基线处理中模糊度解算不同，在网络实时动态 （real time kinematic，RTK）基线处理中，基线偏差很小，先验精度比较高，高精度定位模型也存在一定的区别。

本文通过对GPS中轨MEO卫星，BDS高轨GEO/IGSO卫星角速度的比较，详细分析了BDS高精度定位模型中出现病态性问题的原因。针对这种问题，通过对两个天顶对流层参数加以约束，提出了基于部分岭估计的模糊度浮点解快速解算的改进方法。实验算例的结果表明，在利用GEO/IGSO卫星快速高精度定位时，该方法能够提高模糊度浮点解的精度，进而缩小LAMBDA算法的搜索空间，提高模糊度固定解的合格基线方差比 （即Ratio）值。因此，本文探讨的是制约BDS高精度定位的本质问题和改进方法，是进一步研究BDS与其他GNSS技术融合高精度定位的基础，具有理论意义和实际应用价值。

2 GEO/IGSO载波相位双差定位模型

在网络RTK长基线处理中，采用的载波相位双差观测值能够消除接收机钟差和卫星钟差。当距离较长时，由于对流层延迟很难用模型较好消除，所以引入天顶对流层参数进行估计。而对于电离层延迟，可以采用电离层无关的线性组合来削弱影响。

假设基站p，q观测共视卫星有n＋1颗，并且选择参考卫星编号为k，单历元载波双差网络RTK L1模糊度解算误差方程可表示为

式中

▽（·）为单差算子，▽Δ（·）为双差算子，MF（·）为 映 射 函 数，▽MF）＝MF）－MF），ZTD为测站的天顶对流层湿延迟，λ、N分别表示L1载波波长和模糊度，λW、λN分别表示宽巷波长和窄巷波长，φIF、φ1、φ2、ρ、NW分别表示无电离层组合观测值、L1相位观测值、L2相位观测值、卫地距、宽巷模糊度、▽ΔTD为双差对流层延迟干分量，可以用模型估计，f1、f2分别为L1载波频率和L2载波频率。

式 （1）为一个历元的误差方程，可简写为

因此，对于单个历元，共视卫星n＋1颗，可列n个误差方程，而存在2个映射函数参数，以及n个双差模糊度参数，共n＋2个未知参数，无法用单历元求解。所以需要多历元解算，解算方法可以使用序贯最小二乘。

3 GEO/IGSO双差模糊度模型病态性分析

设两基站连续观测m个历元，共视n＋1颗卫星，在较短的时间内天顶对流层延迟变化不大，因此假设对流层不变。总的误差方程可以表示为

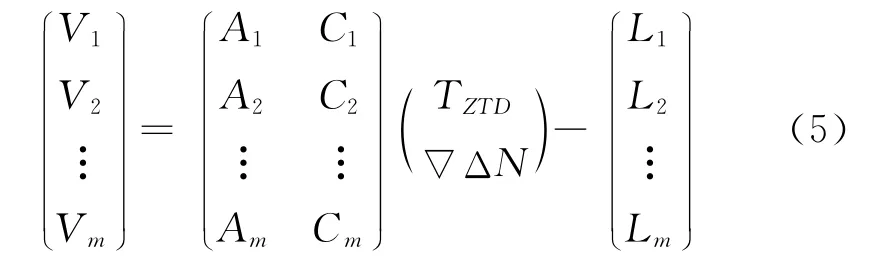
可写成

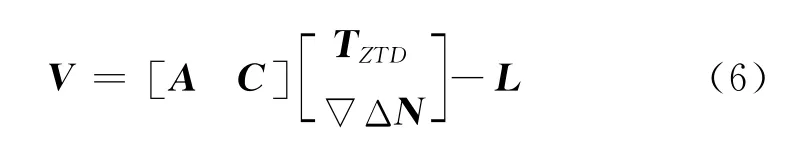
式中，A为s×2维，C为s×n（s＝m×n）维系数矩阵，TZTD为2×1，▽ΔN为n×1维待估参数向量，L为s维双差观测值向量，V为s维残差向量。

在最小二乘准则下，由式 （6）组成法方程，得到无偏待估参数的解为

在主要由IGSO和GEO卫星组成BDS中，由于GEO/IGSO卫星属于高轨卫星，轨道高，运行速度慢，特别是GEO卫星，运行轨迹变化相对缓慢，运行角速度变化并不显著，如图2及图3所示。一方面由于卫星结构变化缓慢，另一方面，又由于对流层延迟变化不明显，导致当法方程行列式的绝对值很小时，一旦Naa，W有较小扰动，就会使得参数解有较大扰动，即导致观测方程出现病态性问题。

图1 GPS运行角速度

图2 IGSO运行角速度

图3 GEO运行角速度

图1表示的是GPS G01号卫星角速度从2012年6月27日0点至24点的变化情况，图2是IGSO C06号卫星角速度从2012年7月19日9点至7月20日1点变化情况，图3是GEO C05号卫星角速度从2012年7月19日9点至7月20日20点的变化情况。

从图1、图2及图3可以看出，MEO G01卫星的角速度最大，IGSO C06卫星次之，GEO C05号卫星最小，与实际情况相符。

模型的病态性可由法方程的条件数来表示。条件数是病态性的一种度量指标。文献 ［10］给出了一个经验数量标准，即0＜cond（N）＜100，认为没有病态性；100≤cond（N）≤1000，认为存在有中等程度或较强的病态性；cond（N）＞1000，则有较严重的病态性 （cond（N）表示方程N的条件数）。本文采用法方程的条件数来衡量定位模型的病态性。

实验通过数据模拟的方式，分析GPS和GEO/IGSO定位的病态性问题。以东南大学礼西楼顶点 （32.058°N，118.789°E）为参考站 A，以距离A站5km的倍数，方位角沿东方向每隔5km取点，构造出B点的坐标。分析基站距离由5－200 km，观测时间由5－30min的基站模糊度解算中单GPS和单BDS的结构及区别，如下图所示 （由于条件数值比较大，采用了条件数的自然对数）。

图4 GPS条件数

图5 BDS条件数

图6 BDS－GPS条件数

从图4、图5及图6中可以看出，随着基站间距离的增加和观测时间的延长，GPS和BDS条件数都降低。这是由于基站间距离增加，两个基站天顶对流层延迟相关性减弱，病态性降低。又由于观测时间越长，卫星空间几何结构变化越明显，病态性也降低。同时可以看出，载波双差解算中，BDS的法方程条件数相应要大于GPS的条件数，且随着距离的增加和时间的延长，两者的差异性越来越大。由此也反映了BDS中GEO/IGSO卫星运行速度慢，卫星结构变化缓慢，病态性较GPS MEO卫星严重的特点。如果不进行改进，应用序贯最小二乘求解时，模糊度浮点解的精度很低，与准确值相差较大，严重影响网络RTK的初始化时间以及导航定位的精度和效率。

4 基于部分岭估计的病态性改进方法及实验验证

载波双差定位模型

在实际的平差问题中，法方程系数阵的行列式不应为零，但它的绝对值可能很小，条件数很大，使得参数解很不稳定。

岭估计是从减小均方差的角度出发而提出的一种有偏估计方法［11-12］，部分岭估计是基于岭估计思想的一种新的有偏估计方法［4］。文献 ［13］给出了均方差意义下有偏估计解由优于传统最小二乘的条件。未知参数的部分岭估计解为

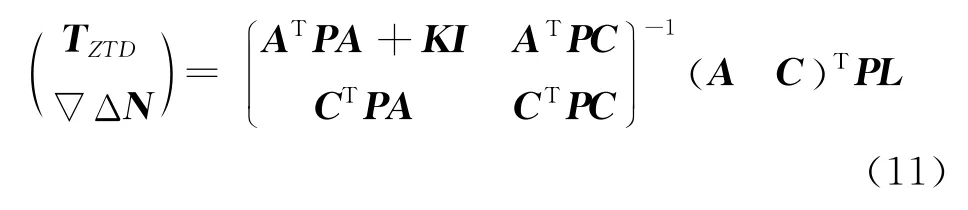
由式 （11）可知，部分岭估计是在最小二乘估计的法方程系数阵Naa的主对角线对流层项上加上一个常数k，从而改变法方程系数阵的态性。

为了验证本文中针对GEO/IGSO卫星高精度定位病态性问题提出的基于部分岭估计的模糊度浮点解快速解算方法，进行了大量的实验。通过选取不同的岭参数k值，计算对应的Ratio值来衡量模糊度解算的准确程度。

实例1中，基线长度20km，采样率5s，高度截止角为10°，观测时间从1min到5min，观测到6颗卫星，分别为C01，C03，C04，C06，C07，C08，参考卫星为C08。k值的选取从0到1，分别计算对应的Ratio值，如图7所示。

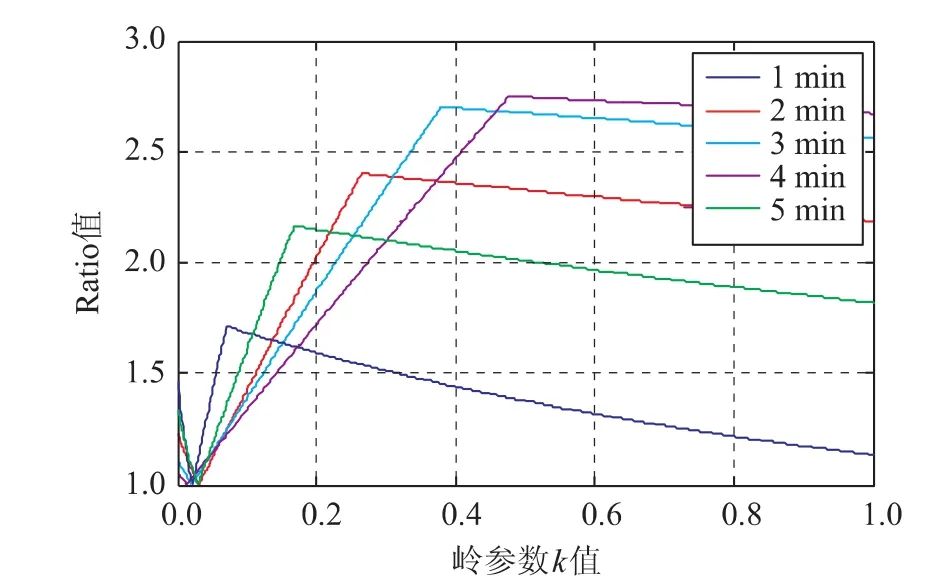
图7 不同观测时间不同k值的模糊度解算情况

实例2中，基线长度20km，采样率5s，高度截止角为10°，观测时间从1min到5min，观测到6颗卫星，分别为C01，C03，C04，C06，C08，C09，参考卫星为C06。k值的选取从0到1，分别计算对应的Ratio值，如图8所示。

图8 不同观测时间不同k值的模糊度解算情况

从图7及图8可以看出，随着观测时间的增加，Ratio值逐渐变大，并且不同的观测时间对应某一具体的岭参数k值，使得Ratio值达到最大。由此可以看出，本文提出的部分岭估计方法确实改善了模型的病态性，提高模糊度浮点解的精度，缩小了模糊度浮点解的搜索空间，进而提高模糊度固定的准确率。在此基础上采用LAMBDA算法可快速准确的固定整周模糊度，减小网络RTK的初始化时间，提高导航定位的精度和效率。

5 结论

本文针对BDS中GEO/IGSO卫星高精度定位模型中病态性问题，通过对两个天顶对流层参数加以约束，提出基于部分岭估计的模糊度浮点解快速解算方法，改善了模型的病态性，提高了模糊度浮点解的精度。实际算例的结果验证了该算法的正确性。但是对于不同长度不同观测时间的基线，如何选取岭参数k值使得Ratio值达到最大，最大程度提高模糊度浮点解的精度是今后进一步研究的内容。

［1］杨元喜.北斗导航卫星系统的进展，贡献与挑战［J］.测绘学报，2010（2），39（1）：1－6.

［2］RAN Cheng－qi.Development of BeiDou Ravigation Satellite System［C］//National Academy of Engineering.Global Navigation Satellite Systems：Report of a Joint Worksho Pof the National Academy of Engineering and the Chinese Academy of Engineering.Washington，D.C.：The National Academies Press，2012：17－24.

［3］OU J，WANG Z.An Improved Regularization Method to Resolve Integer Ambiguity in Rapid Positioning Using Single Frequency GPS Receivers［J］.China Science Bulletin，2004，49（2）：196－200.

［4］李博峰，沈云中.顾及基线先验信息的GPS模糊度快速解算［J］.测绘学报，2008，37（4）：423－427.

［5］TEUNISSEN P J G.The GPS Integer Least－squares Statistics［J］.Physics and Chemistry of the Earth，Part A：Solid Earth and Geodesy，2000，25（9－11）：673－677.

［6］TEUNISSEN P J G.A Canonical Theory for Short GPS Baselines.Part I：The Baseline Precision［J］.Journal of Geodesy，1997，71（6）：320－336.

［7］HATCH R R.Instantaneous Ambiguity Resolution［C］//SCHWARZ K P，LACHAPELLE G.Kinematic Systems in Geodesy，Surveying，and Remote Sensing：Symposium No.107Banff，Alberta，Canada，September 10－13， 1990.New York：Springer， 1990：299－308.

［8］HATCH R R.Ambiguity Resolution while Movingexperimental Results.Proceedings of ION GPS－91，4th International Technical Meeting of Satellite Division of the Institute of Navigation， Albuquerque， New Mexico，September 11－13，1991［C］.New Mexico：The Institute of Navigation，Inc.，1990：707－713.

［9］归庆明，韩松辉，吴炳荣，等.双k型岭估计及其在GPS快速定位中的应用［J］.测绘科学技术学报，2006，23（1）：8－10.

［10］陈希孺，王松桂.回归分析－原理方法及应用［M］.合肥：安徽教育出版社，1987.

［11］欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法［J］.测绘学报，2004，33（4）：283－288.

［12］田玉淼，朱建军，陶肖静.修正岭估计方法在测量数据处理中的应用研究［J］.测绘工程，2012，21（1）：7－10.

［13］徐天河，杨元喜.均方误差意义下正则化解优于最小二乘解的条件［J］.武汉大学学报：信息科学版，2004，29（3）：223－226.