Choquet积分与Sugeno积分的不等式关系

冯慧敏，李雪非，吕文静

（1.河北大学 数学与计算机学院，河北 保定 071002；2.河北农业大学 理学院，河北 保定 071001；3.河北大学 新校区管理与建设办公室，河北 保定 071002）

经典测度起源于几何度量，例如长度、面积、体积.经典测度是一个非负的可加集合函数，概率测度是经典测度的一种.在经典测度发展过程中，可加性成为一个争议的对象.在理想的、无误差的理想情况下，经典测度是适用的.而在现实中，测量误差是不可避免的.此外在一些涉及主观判断的问题中，比如从多个投资项目中选择一个进行投资，度量很显然不符合可加性的条件.因此出现了模糊测度，模糊测度用单调性代替了经典测度中的可加性.而以经典测度为基础的勒贝格积分不能适用于模糊测度，与模糊测度相应的是模糊积分［1－3］.Sugeno积分和Choquet积分是2种有代表性的、应用较多的模糊积分.在多指标决策中指标之间经常有交互作用存在，因此这类问题中模糊测度和模糊积分是合适的数学工具［4－9］.在此类问题中，Sugeno积分和Choquet积分中选择哪一个呢？这个问题需要结合当前问题的特点和积分的特点做选择.没有哪一种积分永远是最优的，2种积分各有特点及其适合的实际问题.而实际上在一定条件下，基于这2种模糊积分的决策没有区别.因为在多指标决策中，2种模糊积分满足一个不等式关系，即2种模糊积分值的差不超过1／4.根据该不等式可以认为，在一些情况下，依据2种模糊积分所做出的决策是一样的.

1 预备知识

在多指标决策中，定义模糊测度的集合属于有限集合，因此本文的讨论限于有限集合.先回顾一下模糊测度和模糊积分的基础知识［10－11］.

模糊测度是对经典测度（即可加测度）的推广.

定义1 设X＝｛x1，x2，…，xn｝为非空有限集合，P（X）为X 的幂集，集函数μ:P（X）→（－∞，＋∞），若集函数μ 满足下列条件：

1）μ（Ø）＝0（归零性）.

2）对任意A⊂X，有μ（A）≥0（非负性）.

3）对任意A⊂B，A⊂X，B⊂X，有μ（A）≤μ（B）（单调性），则称μ 为模糊测度，也称为单调测度.

当模糊测度满足μ（X）＝1时，称为正则模糊测度，通常在多指标决策中采用的都是正则模糊测度.

设函数f（x）为定义在集合X＝｛x1，x2，…，xn｝上的非负函数，f:X→［0，1］，μ 为定义在P（X）上的正则模糊测度.假设集合X 中的元素已经经过重排，使得0≤f（x1）≤f（x2）≤…≤f（xn）≤1.令Ai＝｛xi，xi＋1，…，xn｝，根据模糊测度的单调性，显然有1＝μ（A1）≥μ（A2）≥…≥μ（An）≥0.Sugeno积分和Choquet积分的定义如下.

定义2 函数f（x）关于模糊测度μ 的Sugeno积分定义为

定义3 函数f（x）关于模糊测度μ 的Choquet积分定义为

其中f（x0）＝0.

Sugeno积分是以取大、取小算子为基础，因而其光滑性较差，不便于进行解析分析.Choquet积分是以乘、加算子为基础，因而其光滑性较好，便于进行解析分析.而且当模糊测度退化为经典测度的时候，Choquet积分可以与勒贝格积分完全一致.

2种模糊积分均满足有界性，即

1.5 疗效判定指标[6] 痊愈：B超检测子宫大小、胎儿大小与孕周基本符合，BPD、FL及S/D比值都有明显改善，双侧RI均<0.8；有效：B超检测子宫大小、胎儿大小与孕周基本符合，BPD、FL、RI及S/D比值都有所改善；无效：B超检测胎儿发育不良或停止发育，BPD、FL、RI及S/D比值均无改善。

2 2种模糊积分的不等式关系

定理1［11］设X＝｛x1，x2，…，xn｝为有限非空集合，函数f 满足：f：X→［0，1］，μ 为定义在幂集P（X）上的正则模糊测度，则有

该定理表明，对于正则模糊测度，值域在［0，1］区间内的函数的Choquet积分和Sugeno积分的值相差不大.在多指标决策、群决策中，恰好可以满足定理的条件.下面对该定理进行证明.

证明 假设被积函数f（x）已经满足0≤f（x1）≤f（x2）≤…≤f（xn）≤1（如果不满足，可以对集合X 中的元素进行重排，使其满足）.令Ai＝｛xi，xi＋1，…，xn｝，显然根据模糊测度的单调性有1＝μ（A1）≥μ（A2）≥…≥μ（An）≥0.下面分6种情况分别证明.

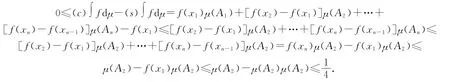
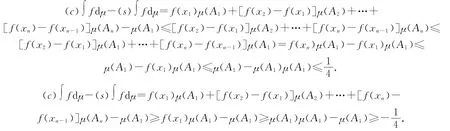
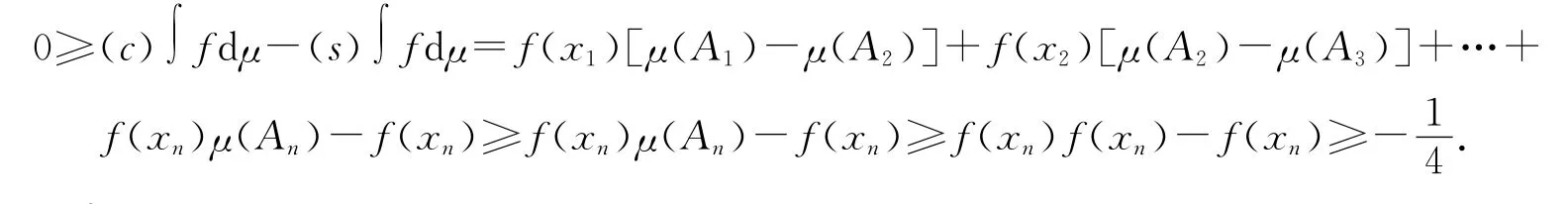
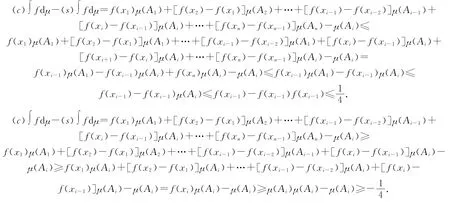
证毕.

3 讨论

在专家系统、多分类器融合、多指标决策等类似问题中，多数都是使用正则模糊测度.此时被积函数f（x）在不同问题中，可有不同解释，如各个专家对于自身决策的把握程度、各分类器认为待分类对象属于各个类的概率（或可能性）、待评价目标与各个指标的符合程度.通常被积函数f（x）满足取值在［0，1］区间内的要求，因此Choquet积分和Sugeno积分的不等式关系适用于这些问题.该不等式说明，在一些情况下2种模糊积分的决策结果是一样的.下面举例说明：

例1：设有2个投资项目A，B，请专家分别对2个项目从低风险（x1）、高收益（x2）、可行性（x3）3个方面进行评估，专家的评分结果列于表1.项目负责人认为评价项目的各指标的重要性通过一个模糊测度表示，该模糊测度定义在指标集合上.

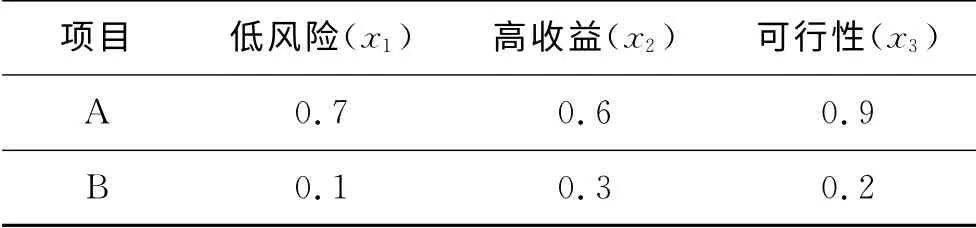
表1 专家对2个项目的评分Tab.1 Scores of two projects from experts

表2 指标的重要性（即模糊测度μ）Tab.2 Degree of criteria（fuzzy measureμ）

将专家从3个指标对项目A，B的打分分别看做被积函数，关于表2中的模糊测度求Choquet积分得

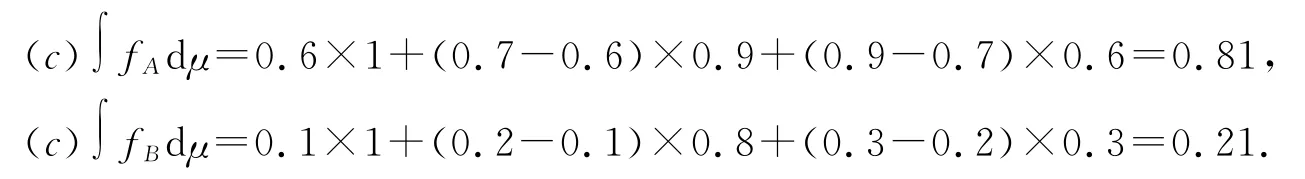
显然项目A 的总评分0.81高于项目B 的总评分0.21，因此最终的决策结果是项目A.根据定理1可知，如果采用Sugeno积分，则项目A 的总评分在区间［0.81－0.25，0.81＋0.25］内，即［0.56，1］（因为由模糊积分的有界性可知，积分最大取值为1.），而项目B 的总评分在区间［0.21－0.25，0.21＋0.25］内，即［0，0.46］（因为由模糊积分的有界性可知，积分最小取值为0）.即采用Sugeno积分时得到的决策结果仍然是项目A.2种模糊积分的决策结果相同.采用Sugeno积分时，实际计算的项目A，B的总评分分别为0.7，0.3.

定理1表明，对于多指标决策问题，当一种模糊积分的决策结果比较清晰时（0.81与0.21的差别比较大的情况），那么2种模糊积分的决策结果是一样的.此时不用费力地去选择模糊积分，而是应该着重研究、分析系统的其他方面，例如指标的增减、指标的重要性是否恰当等等.

4 结论

本文证明了在多指标决策、多分类器融合环境下Sugeno积分和Choquet积分之间的不等式关系.不等式表明在决策结果比较清晰时2种模糊积分的决策结果是一致的，此时应当将更多的精力用于指标的增减或者分类器的增减，以及模糊测度的定义方面.

以Sugeno积分和Choquet积分之间的不等式关系为基础，下一步可以围绕如何找到一个指标将决策问题分成2类，一类是2种积分的结果相同的问题，另一类是2种积分的结果不同的问题，并比较在结果不同的一类问题中，哪种积分的结果更合理.这些结果将对模糊积分的应用提供帮助.

［1］ SUGENO M.Theory of fuzzy integrals and its applications［D］.Tokyo：Tokyo Institute of Technology，1974.

［2］ SUGENO M，MUROFUSHI T.Choquet integral as an integral form for a general class of fuzzy measures［Z］.Proceedings of Second IFSA Congress，Tokyo，1987.

［3］ 尤翠莲，王根森.一类新的模糊积分的性质［J］.河北大学学报：自然科学版，2011，31（4）：337－340.YOU Cuilian，WANG Gensen.The properties of a new kind of fuzzy integral［J］.Journal of Hebei University：Natural Science Edition，2011，31（4）：337－340.

［4］ 李雪非，顾志华，冯慧敏.模糊积分分类器中的自适应模糊测度［J］.河北大学学报：自然科学版，2012，32（4）：342－348.LI Xuefei，GU Zhihua，FENG Huimin.Self－adaptive fuzzy measure for fuzzy integrals classifiers［J］.Journal of Hebei University：Natural Science Edition，2012，32（4）：342－348.

［5］ GRABISCH M，SUGENO M.Multi－attribute classification using fuzzy integral［Z］.1st IEEE International Conference on Fuzzy Systems，San Diego，1992.

［6］ GRABISCH M.Fuzzy integral in multicriteria decision making［J］.Fuzzy Sets and Systems，1995，69：279－298.

［7］ 王熙照.模糊测度和模糊积分及在分类技术中的应用［M］.北京：科学出版社，2008.

［8］ ANDREY Temko，DUSAN Macho，CLIMENT Nadeu.Fuzzy integral based information fusion for classification of highly confusable non－speech sounds［J］.Pattern Recognition，2008，41（5）41：1814－1823.

［9］ WANG Lijuan.An improved multiple fuzzy NNC system based on mutual information and fuzzy integral［J］.International Journal of Machine Learning and Cybernetics，2011，2（1）：25－36.

［10］ WANG Zhenyuan，GEORGE J KLIR.Fuzzy measure theory［M］.New York：Plenum Press，1992.

［11］ MUROFUSHI T，SUGENO M.Fuzzy measures and integrals［M］.New York：Pyhsica Verlag，2000.