软组织形变模型的自适应网格细分算法
刘秀玲,陈栋,董亚龙,董斌,王洪瑞
(1.河北大学 电子信息工程学院 医工交叉研究中心,河北 保定 071002;2.河北大学附属医院 计算机中心,河北 保定 071000)
随着计算机图形学技术、数字图形处理技术、虚拟现实技术等技术的快速发展,虚拟手术作为一个多学科交叉的新领域,越来越广泛地应用到医学手术的训练和相关医学的研究中.虚拟手术训练要达到与传统训练同样的效果,就必须保证虚拟仿真过程的实时性和模型的真实感,因而建立一个快速、高效、精确的软组织模型是虚拟形变仿真中最为关键的一部分[1-2].
三角网格模型因其具有简单的模型结构、较好的通用性及网格稳定性,广泛应用在真实感图形模型的构建中.三维网格细分曲面模型是在原始三角网格曲面基础上经过网格细分算法获取的曲面模型,使得经过处理之后的三角网格模型更准确地描述三维物体的几何特性和物理特征.国内外的学者对模型细分的方法进行了大量研究,并提出了大量的著名方法,如Loop细分法[3-4],Buterfly细分算法[5].Sederberg等[6]在B 样条构建方法的基础上引入了非均匀节点区间的概念,提出了非均匀细分曲面的方法.Zorin在经典的Butterfly算法的基础上进行改进使得网格模型具有更为光滑的特性[7].张文明等[8]提出了局域Delaunay剖分的动态点单元一体化三维网格的自适应生成算法,使得模型可以准确地反映出三维物体的几何特征[8].然而,常见的三角网格加密技术是对整体模型处理,虽然可以达到较为真实的形变效果,但是大幅增加了计算形变所需的时间.
本文采用了Loop三角网格细分算法对软组织模型形变区域进行局部处理,使得形变区域三角网的密度增加,在保证形变快速性的基础上,提高了软组织发生形变时的形变精确度和视觉沉浸感;同时对该区域的三角网格进行拉普拉斯平滑优化处理,从而进一步提高了形变区域形变效果的真实程度.实验结果表明该算法是准确有效的,能够较好地兼顾软组织形变对准确性和快速性的要求.
1 Loop网格细分算法
三维模型的表面网格大多数采用的是三角形网格的形式,网格中三角面片的大小、形状直接影响模型的逼真程度.经过网格细分之后的模型三角网格能够精确地表达复杂模型表面的形体特征.细分方法具有一些主要的特点,可以概括为5个方面:拓扑的适应性;可伸缩性;网格唯一性;数值稳定性;实现简易性.将网格细分后的软组织模型应用到虚拟手术训练系统中,不仅可以反映软组织的几何特性,还可以在软组织受力形变的仿真过程中更精确地体现出组织表面形变的效果.
本文对软组织进行网格自适应细分的方法就是基于经典的Loop网格细分算法.Loop细分算法采用的拓扑规则是在每一个三角形网格的每一条边上插入1个新顶点,再将各个顶点连接起来,将1个三角面片细分为4个,新生成的网格数量是原始网格数量的4倍,这种方式只生成了2种顶点,即边生成的新顶点(E-顶点)和原来的顶点(V-顶点)[9].
Loop算法的顶点获得的规则如下:
1)内部边生成的点E-顶点:设内部边的2 个顶点分别为ν0,ν1,由此边组成的三角形为Δν0ν1ν2和Δν0ν1ν3.则E-顶点定义为
2)边界边生成的点E-顶点,设该边是由顶点ν0,ν1组成,则
3)对于每个内部顶点V-顶点,设其相邻顶点为ν0,ν1,…,νn,那么得到的顶点V-顶点为νv=(1-nβn)ν+其中βn 为邻点权值,定义为
Loop细分算法生成的4类顶点如图1所示.
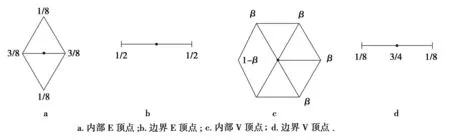
图1 Loop细分算法Fig.1 Loop subdivision algorithm
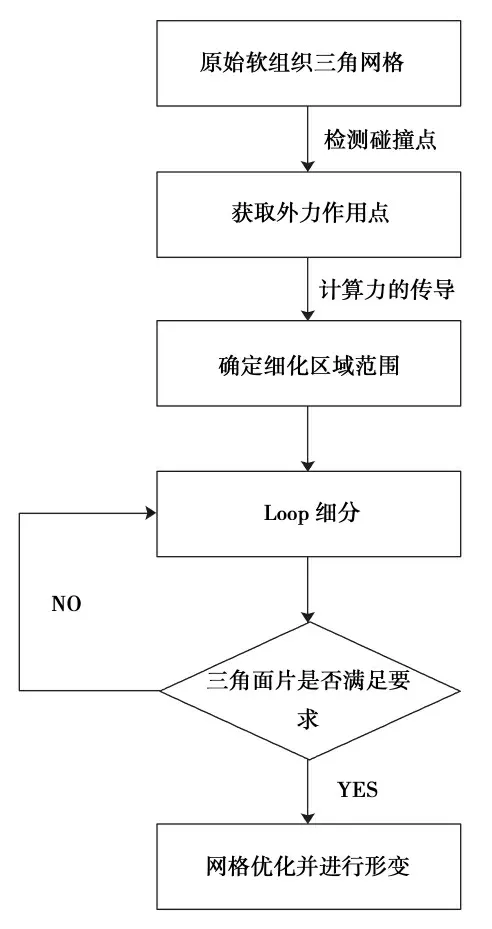
图2 基于Loop的自适应网格细分及优化Fig.2 Subdivision and optimization based on the Loop subdivision algorithm
2 自适应网格细分算法的设计与实现
软组织形变模拟时用到的模型网格与一般实体模型网格所要达到的目的有所不同.通常模型网格划分的目的是为了更准确地描述出三维物体的几何特性和物理特性,而形变模型不仅要反应出软组织的外形特征,还要针对外力的作用对形变区域进行自适应的网格加密,才能更准确地模拟形变效果.
2.1 自适应网格细分算法概述
通常自适应网格细分技术的应用是为了描述几何体的几何特征,对几何体局部网格进行细分.而本文在软组织形变仿真中,自适应网格细分技术应用在针对形变区域的精细化操作中,目的是为了保证形变的真实性和良好的视觉效果.
曲面的细分是从原始的三角网格数据出发,根据预先设定好的细分迭代规则,在给定区域三角网格内插入新的顶点,然后将这些行新顶点连接形成新的三角网格数据,实现对原始三角网格的细分效果.
首先要确定网格细分区域,然后为避免在新细分出的三角网格内出现“较大”的三角面片,对需要进行进一步细分的三角面片制定了一个细分规则,最后将满足要求的三角网格重新用Delaunay三角剖分方法进行重构,使得经Delaunay三角剖分之后的三角网格质量饱满并且具有唯一性,最终达到理想的自适应网格细分效果.算法实现的步骤如下:1)识别细分区域边界,利用Loop细分算法添加新的顶点.2)区域内的所有顶点进行Delaunay三角剖分,构建新的三角网格.3)判断三角网格中的三角面片是否满足要求,对不满足要求的三角面片继续进一步细分操作.
自适应网格算法的设计流程如图2所示.
2.2 网格细分区域范围的划定
与以往自适应网格划分区域的目的不同,本文细分区域的划定是为了保证形变区域在形变计算后形变效果的逼真,所以,网格加密区域范围的划定就是根据外力的值对模型表面形变区域的确定过程.当外力作用在模型表面的某一位置时,根据质点弹簧模型的力学方程式中,Fij表示质点i,j之间的弹簧力;K 为弹簧的弹性系数;Lij为2个质点之间静止时原有的距离;pi,pj分别为质点i,j的三维坐标向量.求得质点间的相互作用力,以及力在模型表面的传导范围,当某2个质点的力小于0.01N 时,视为外力到达作用边界,不会再向外围继续传导.如图3所示,假设外力作用位置为图中点1的位置.
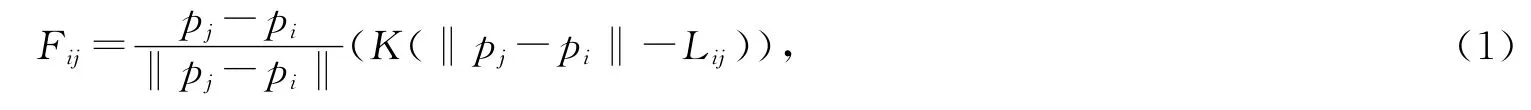
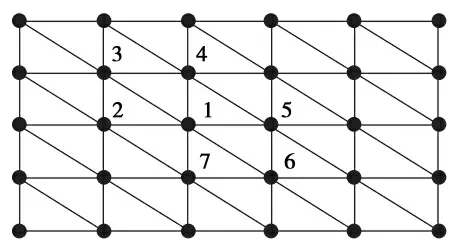
图3 模型表面三角网格Fig.3 Triangle mesh of surface model
1)假设该质点周围的质点是固定的,根据公式(1)计算出该点的虚拟位移量;
2)目标质点的移动会对周围6个质点产生弹簧拉力作用,根据这个拉力逐个计算出与目标质点相连的其他6个质点的虚拟位移量.返回1),重复计算,直到包括目标质点在内的7个质点相对平衡为止;
3)分别以2,3,4,5,6,7作为目标质点,逐个计算与其相连质点的虚拟位移量,进行力的传导.返回1),直到这些质点都到达力的平衡位置.
在这种方法中,力的计算只是为了获取作用力的影响区域,质点的位移并没有显示在界面上,因而不会对模型的渲染造成影响.最终获得的这个影响区域就是需要进行网格细分的区域.如图4所示,中心深色区域即外力为10N 时的需要进行细分区域.
2.3 基于几何特性的细分规则制定
由于原始三角网格中的每个三角面片大小未必一致,为达到更好的三角网质量,要使经过细分之后生成网格的三角面片具有较为一致的几何形状,为此,需要对细化区域内的三角面片是否需要进一步细化进行判断.
设细分区域内的某一个三角形边长为l1i,l2i,l3i,当max(l1i,l2i,l3i)>α时,则该三角面片需要进一步细分处理.α为设定的一个固定值,用来控制细分后三角网格中每个三角形的最大边长.
3 实验结果及分析
在CPU:Pentium E2200 2.20GHz,内存2G,显卡NVIDIA Geforce 9700GT,显存512 MB 的PC 机上,以VTK 可视化工具包为基础,用VS2005作为开发环境,实现本文提出的自适应网格生成及优化算法.
如图4所示,在确定细分区域之后,将本文算法应用到该区域的软组织模型表面上进行网格细分,得到的三角网格如图5所示.

图4 网格细分区域的划定Fig.4 Subdivision area of the model
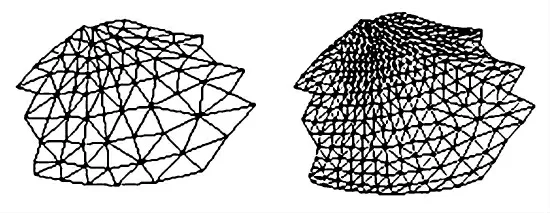
图5 原始的三角网格与细化后的三角网格Fig.5 Original mesh and subdivision mesh
进一步验证本文算法生成的模型网格在形变仿真时的实时性,将原始的软组织表面模型整体进行Loop网格细分,与本文方法进行对比.将外力作用在同一位置上,随着作用力逐渐增大,受力质点达到稳定所消耗的时间也逐渐增大,记录数据得到表1.绘制出作用力与消耗时间的对比图,如图6所示.由实验数据可以得出,本文提出的自适应网格细分算法,具有良好的仿真实时性,大幅缩短了采用传统加密方法时消耗的时间.

表1 形变仿真耗时Tab.1 Time of deformation simulation
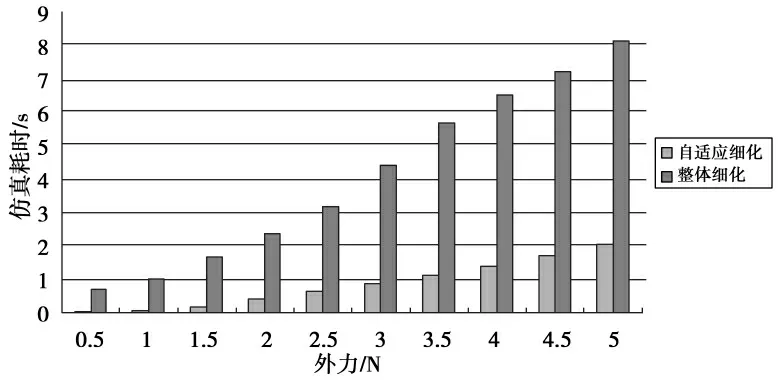
图6 变形仿真耗时柱状图Fig.6 Time of deformation simulation
软组织表面在形变过程中,经过三角网格细化后的模型对于形变效果的表达能力有了一定的提高,但模型表面依然会出现“棱角”现象,如图7a所示.为消除这种现象,对软组织表面模型进行拉普拉斯平滑优化处理,经过优化后的模型效果如图7b所示.对模型采取平滑优化处理之后这种棱角得到了很好的解决,增强了变形的真实性,保证了虚拟手术训练对沉浸感的要求.
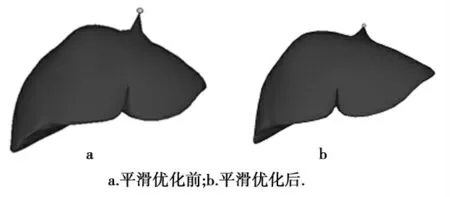
图7 软组织表面模型形变效果Fig.7 Deformation effect of soft tissue surface model
4 结论
本文提出的三角网格自适应加密算法,较好地保证了形变结果的精确性,同时大大缩短了形变计算的时间,并且应用平滑优化技术使得模型表面更加光滑、平顺,提升了视觉的沉浸感.为了进一步提高虚拟手术训练系统的整体性能,将对形变模型的结构特点和受力特点进行更深一步的研究;完善网格细分的规则,使细分出的三角网格质量更均匀;采用CUDA 并行技术提高形变计算的速度;对碰撞检测程序进行修改,保证碰撞检测的快速和精确.
[1] SEMERARO F,BERGAMASCO M,FRISOLI A,et al.Virtual reality prototype in healthcare simulation training[J].Resuscitation,2008,77(1):S60-S61.
[2] ROMERO G,MAROTO J,FELEZ J,et al.Virtual reality applied to a full simulator of electrical sub-stations[J].Electric Power Systems Research,2008,78(3):409-417.
[3] LOOP C.Smooth subdivision surfaces based on triangles[D].Salt lake City:University of Utah,1987.
[4] CHENG F,FAN F,LAI S.Loop subdivision surface based progressive interpolation[J].Journal of Computer Science and Technology,2009,24(1):39-46.
[5] DYN N,LEVIN D,GREGORY J A.A butterfly subdivision scheme or surface interpolatory with tension control[J].ACM Transactions on Graphics,1990,9(2):160-169.
[6] SEDERBERG T,ZHENG J,SWELL D,et al.Non-uniform recursive subdivision surfaces[Z].In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques,New York,1998.
[7] 贾太峰.基于任意拓扑网的细分改进算法研究[D].无锡:江南大学,2008.JIA Taifeng.The subdivision research on improved algorithm over arbitrary topological meshes[D].Wuxi:Jiangnan University,2008.
[8] 张文明,刘彬,徐刚.三维实体网格自适应划分算法[J].机械工程学报,2009,45(11):266-270.ZHANG Wenming,LIU Bin,XU Gang.Three dimensional entity mesh generation algorithm[J].Journal of Mechanical Engineering,2009,45(11):266-270.
[9] 潘青,徐国良.常平面曲率细分曲面的构造[J].计算机辅助设计与图形学学报,2011,23(6):964-970.PAN Qing,XU Guoliang.Construction of constant mean curvature subdivision surfaces[J].Journal of Computer-aided Design &Computer Graphics,2011,23(6):964-970.

