滚滑轴承螺旋空心滚子受力变形的理论研究

卢黎明

(华东交通大学 机电工程学院，南昌 330013)

1 滚滑轴承结构及特点

机械装备中使用的轴承大部分是滚动轴承和滑动轴承。这两种轴承各有优、缺点，滚动轴承的优点主要在于启动摩擦阻力小、维护方便、适用于中低速状态下工作,最大缺点是承受冲击载荷能力差;动压滑动轴承的优点主要在于承受冲击载荷能力强，摩擦因数小,结构简单，适用于中高速状态下工作,最大缺点是启动和低速时摩擦阻力大。

滚滑轴承是一种新型轴承[1-2]，如图1所示。其主要由内圈、外圈、螺旋空心圆柱滚子和滑块构成[3]，兼有滚动轴承和滑动轴承的优点，能更好地适应低速重载的工作条件。其中螺旋空心圆柱滚子的主要作用是使轴承保持滚动轴承的优良特性，如良好的启动性能和高速稳定性；而滑块的主要作用是使轴承保持动压滑动轴承的优良特性，如较高的承载能力、较长的使用寿命。滚滑轴承的工作性能与其零部件之间的摩擦性能有很大关系，由于螺旋空心圆柱滚子径向受压后会产生径向和轴向变形，这必定会影响滚子端面与套圈挡边之间的摩擦。为此，对滚滑轴承螺旋空心圆柱滚子径向受压后的径向和轴向变形情况进行研究。

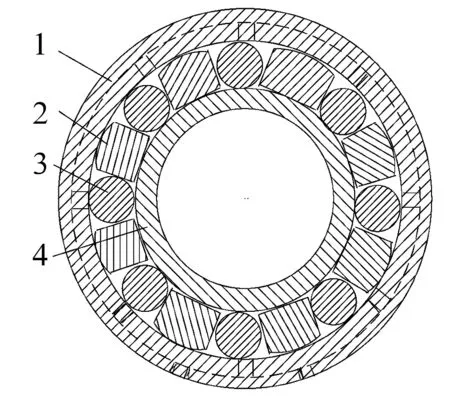
1—外圈；2—滑块；3—螺旋空心圆柱滚子；4—内圈

2 滚子受力分析

螺旋空心圆柱滚子一般由窄钢带卷制而成，工作中主要受内圈的径向冲击载荷。因滚子受冲击时处于收缩状态，滑块作用在滚子上的力很小,可忽略不计；另外，滚子与滚道之间存在微滑动，但滚道表面有润滑油，摩擦阻力很小，也可忽略不计。因此，螺旋空心圆柱滚子的受力可简单视为受内、外圈作用的一对平衡力。由于滚子是正弦周期性螺旋状，每圈钢带情况相同，每圈钢带又可分成完全相同的4部分，每部分都是从与套圈接触的接触点到中间的部分，每部分的受力情况相同，而且每部分的结构和受力相同，故对整个滚子的分析可简化为对1/4圈窄钢带的分析。每圈钢带的轴向伸长量为1/4圈钢带轴向伸长量的4倍。假定套圈(内圈或外圈)与每圈钢带上的作用力为2Fr，则1/4圈钢带与套圈接触处的一端受力为Fr。在1/4圈钢带上取一斜截面A,设该截面中心到Fr作用力线的垂直距离为ζ，对斜截面A进行分析[4]，可知斜截面A上作用有弯矩M=Frζ和与径向力Fr平行作用于截面中心大小为Fr的水平力，如图2所示。

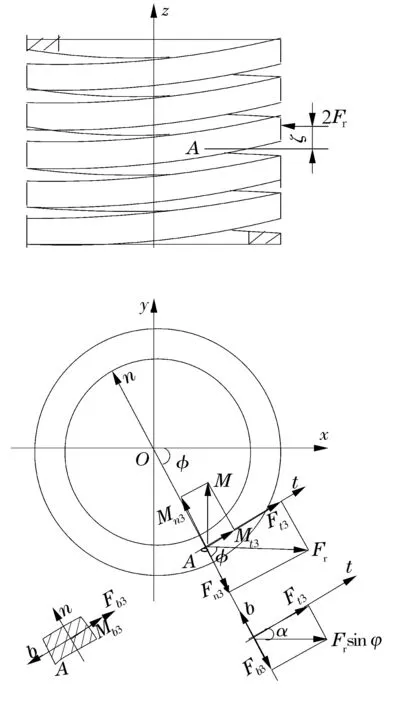
图2 螺旋滚子受力简图

在斜截面A上，建立如图2所示的btn坐标系，M和Fr可分解为

(1)

(2)

Mn3=Msinφ=Frζsinφ，

(3)

Ft3=Frsinφcosα，

(4)

Fb3=-Frsinφsinα，

(5)

Fn3=-Frcosφ，

(6)

式中：Tt3为绕t轴回转的扭矩；φ为滚子螺旋圈自xOz垂直平面至弹簧材料任意截面的极角；α为螺旋圈的螺旋角；D为螺旋圈中径；Mb3为绕b轴回转的弯矩；Mn3为绕n轴回转的弯矩；Ft3为沿t轴作用的截面法向力；Fb3为沿b轴作用的截面切向力；Fn3为沿n轴作用的截面切向力。

3 应力分析

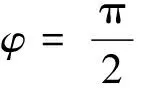
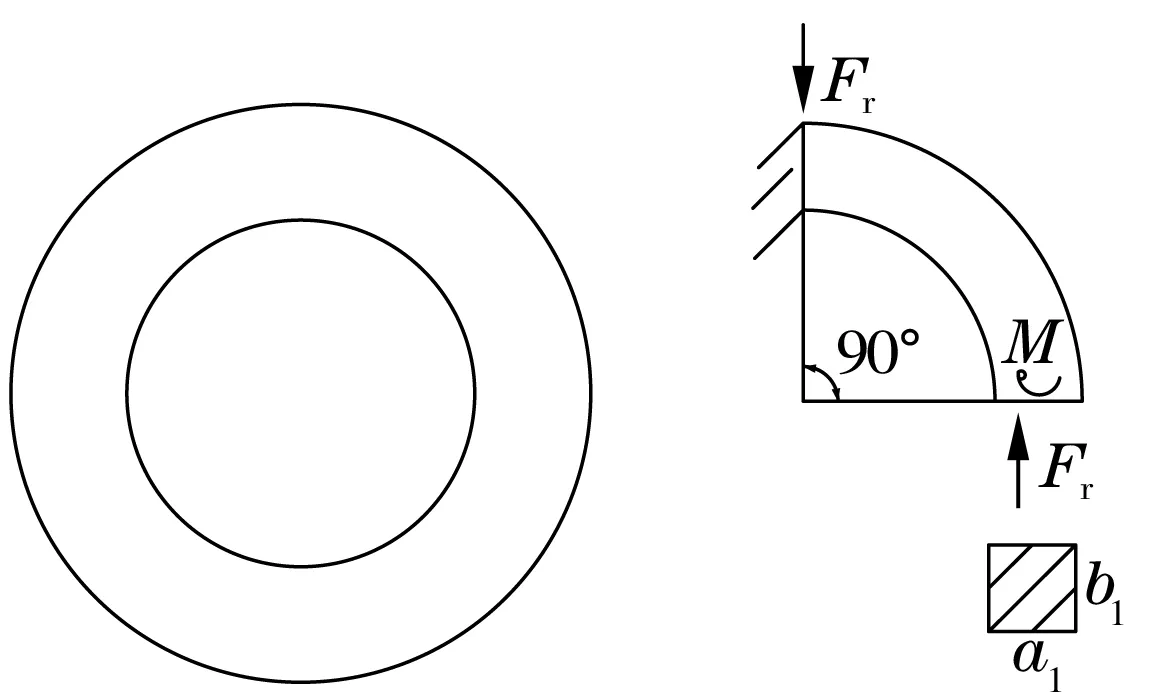
图3 与Fr成90°截面上的应力分析示意图

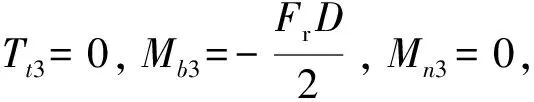
(7)

(8)

(9)

4 变形能分析

滚子承受载荷产生变形，吸收积聚的能量可利用弹簧变形能理论进行计算[4]，

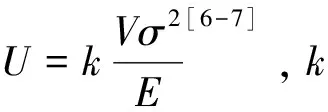
(10)

5 变形分析

根据能量守恒定律，如果忽略摩擦损失，外力Fr作的功应全部转化为1/4圈螺旋空心滚子的变形能，即有

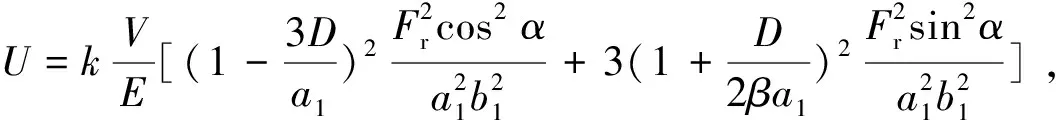
则半径方向位移量δ为

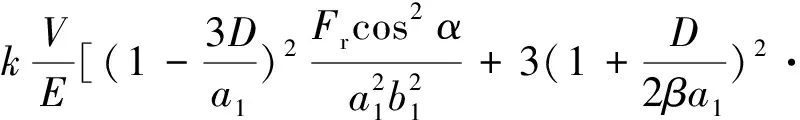
(11)

滚子受力后，轴承将产生径向收缩[8-9]，由(11)式可知弹性滚子中径将变为

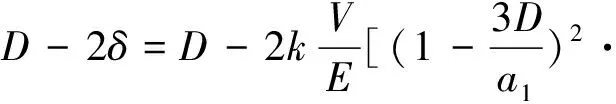
(12)

如图4所示，一圈螺旋空心滚子按平面展开，即为直角三角形，由此可得一圈螺旋空心滚子受力后的伸长量为

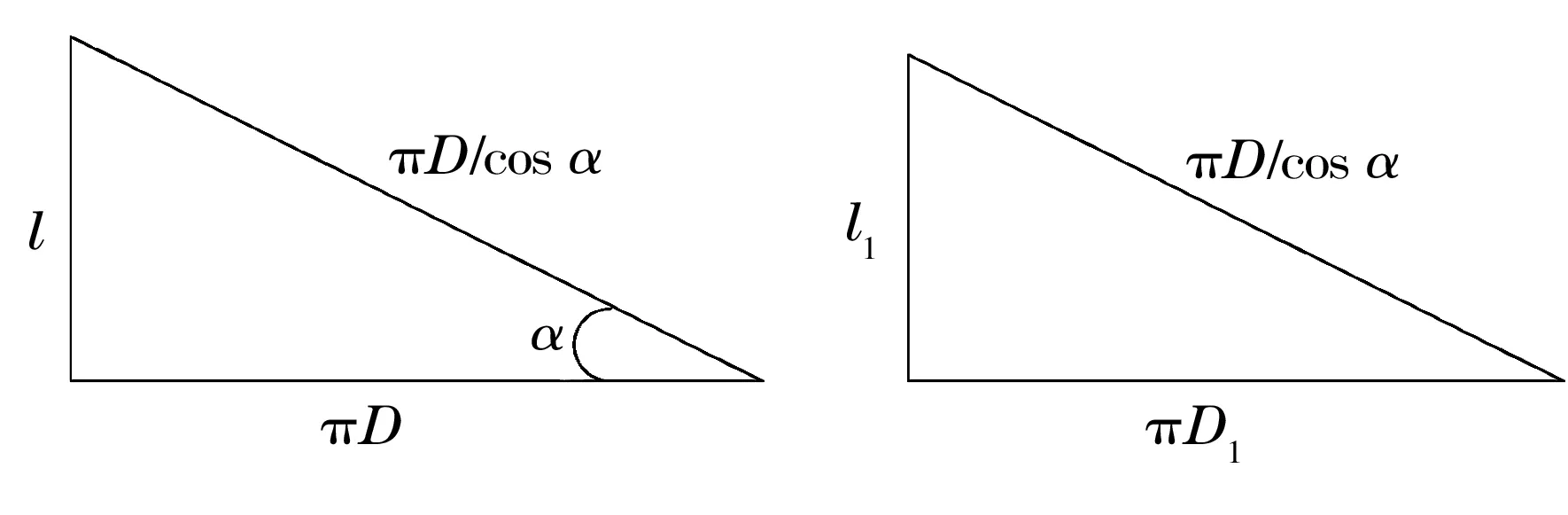
图4 一圈螺旋钢带的平面展开图

(13)

式中：l和l1分别为一圈螺旋空心滚子受力前、后的轴向长度。

n1圈螺旋空心滚子受力后的伸长量为

ΔH=n1Δl，

(14)

则由(12)～(14)式可得

πn1Dtanα。

(15)

6 结束语

螺旋空心圆柱滚子受力后将产生径向收缩和轴向伸长；且径向收缩量和轴向伸长量与螺旋圈中径D、比例系数k、弹性滚子材料的体积V、弹性模量E、横截面厚度a1、横截面高度b1、螺旋角α、与b1/a1有关的系数β和径向作用力Fr等因素有关。另外，利用上述公式，通过实测内圈的最大变动量，可得到螺旋空心圆柱滚子的最大径向变形量、轴向伸长量和任意位置的径向变形量、轴向伸长量，进而可得出螺旋空心圆柱滚子与套圈挡边摩擦力的情况，为进一步研究滚滑轴承的动力学性能提供依据。