双自转研磨沟槽结构参数对球体研磨均匀性的影响分析
郁炜, 吕冰海,李兴林,袁巨龙 ,姚蔚峰
(1.浙江工业大学 机械学院,杭州 310014;2.衢州学院,浙江 衢州 324002;3.杭州轴承试验研究中心 博士后科研工作站,杭州 310022)
精密滚动轴承、滚珠丝杠、滚动导轨广泛应用于精密机械、航空航天、石油化工等领域,精密球是其中的关键零件。但传统球体研磨方法的加工一致性和稳定性差,成本高,因此,迫切需要能够高效、高精度、批量加工精密球体的研磨方法和设备[1-2]。
文献[1,3-4]提出了能实现球体超精密加工的双自转式研磨方法,其从成球原理上保证了精密球体加工的高精度和球批一致性。研制的基于双自转研磨方式的超精密球体研磨设备Olymball-D600,使批量加工的钢、陶瓷和硬质合金球的精度(球形误差、表面粗糙度和球批直径变动量)大幅提高[3]。
数值模拟技术应用在设计制造领域,使研究设计摆脱对物理样机的依赖,实现原型的多样化,扩大了研究范围,降低了研发成本,缩短了研发周期[5]。多体动力学分析软件ADAMS易于非线性动力学分析,方便机械系统性能的参数分析[6],符合双自转研磨过程的仿真分析需求。为进一步改善双自转研磨轨迹点分布均匀性,下文基于ADAMS建立了双自转研磨方式数值仿真模型,分析了下研磨盘结构对研磨均匀性的影响,确定了最佳沟槽半径和沟槽角参数。
1 数值模型的建立
双自转研磨通过控制下研磨盘内、外盘转速的变化组合,使球坯自转角θ在[-90°,90°]内变化,实现研磨轨迹在球面“全包络”[2-3],保证研磨轨迹点均匀分布。双自转研磨原理如图1所示[3],图中,A,B,C分别为研磨盘与精密球的接触点;RA,RB,RC分别为3接触点到研磨盘回转轴的距离;ΩA,ΩB,ΩC分别为研磨盘转速;rb为球半径;Ωb为球体公转角速度;ωb为球体自转角速度;α,β为V形槽沟槽角;R为沟槽半径,R=RA,RB=RA+rbcosα,RC=RA-rbcosβ。
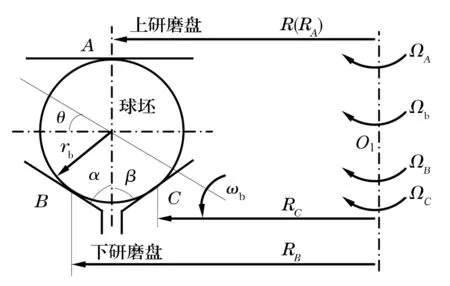
图1 双自转研磨原理示意图
建立的ADAMS数值仿真模型如图2所示, 其中参数化点的变量见表1。为使仿真分析结果尽可能与实际加工结果吻合,根据双自转研磨成球的运动状态,研磨处于精加工阶段,材料去除量和球体几何外形变化都很小,因此,建模时的仿真条件为[7]:(1)忽略研磨过程中研磨液腐蚀等化学作用;(2)忽略材料去除作用;(3)以单个理想真球体作为分析对象;(4)球体与研磨盘之间皆为刚性接触,无相对滑动。

表1 设计变量的含义
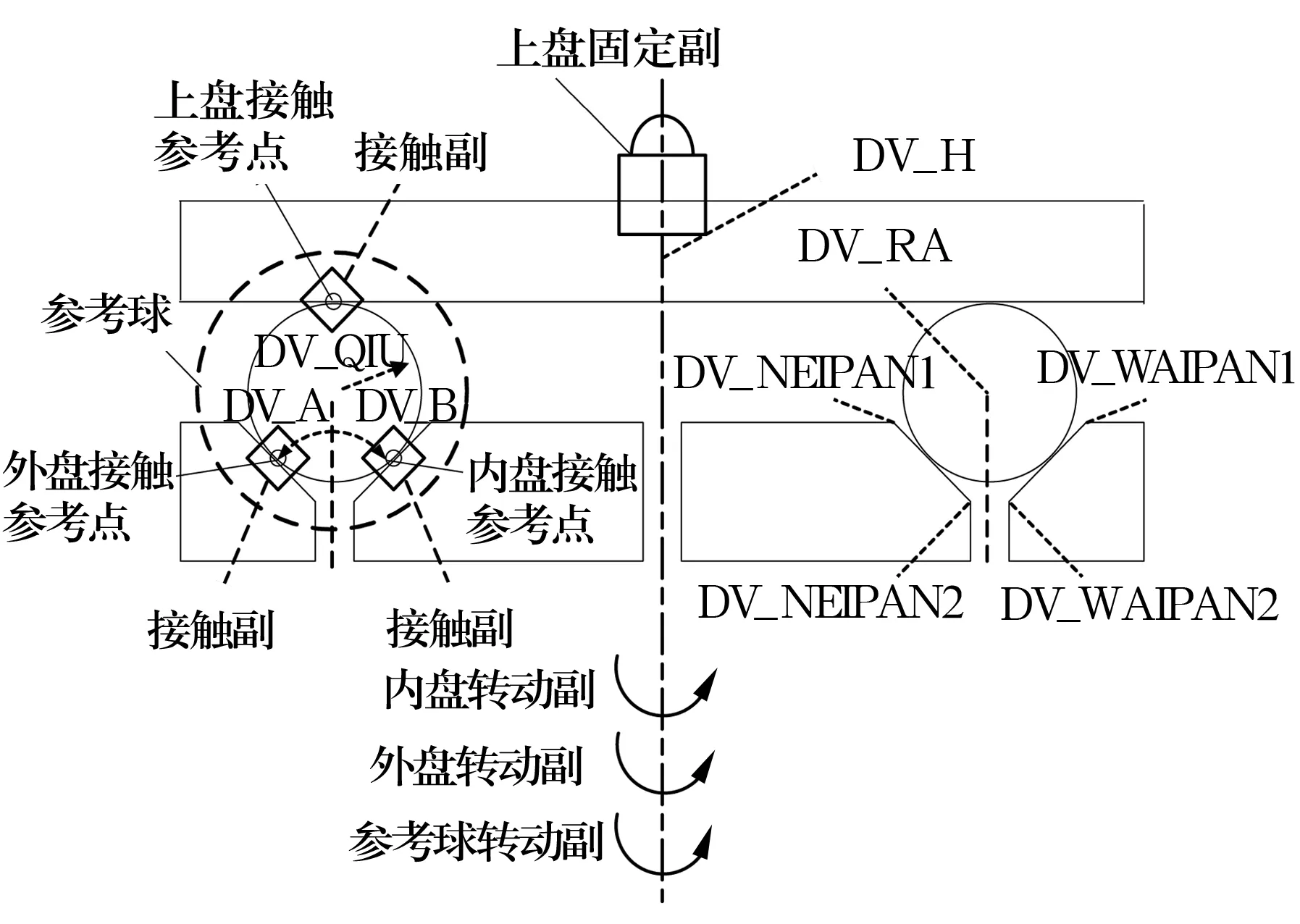
图2 双自转研磨方式数值仿真模型
利用ADAMS软件中自带的系统测量函数进行计算,获得球心在地面坐标系的公转和自转运动状态;在模型参考球上添加转动副和驱动,以解决接触点运动状态测量的问题;将球心公转角速度的数据输入到驱动中;最后将参考点的坐标从地面坐标系转换到球心坐标系,即可绘制出球体的研磨轨迹[5-6]。
为判断研磨轨迹点在球面上均匀分布程度,给出了球面研磨均匀性定量分析评价方法:利用ADAMS模型对球面研磨轨迹进行仿真;对球面进行区域划分,通过数值计算,统计球面每一划分区域内的研磨轨迹点密度;采用统计方法计算各区域内研磨轨迹密度的标准差S值,将其作为球面研磨轨迹均匀性的定量评价值(S越小,轨迹点分布均匀性越好);以研磨轨迹均匀性为目标,采用寻优方法,获得最佳沟槽半径和沟槽角。
采用三角形网格划分球面区域(图3),即把球面划分为若干个形状、面积相同的三角形区域,以每个三角形区域为单位统计研磨轨迹点的数量。研究表明[3,8],当球面划分为128个三角形区域时,既可以获得充分反映球面研磨轨迹点分布均匀性的数据,又可以兼顾仿真效率。
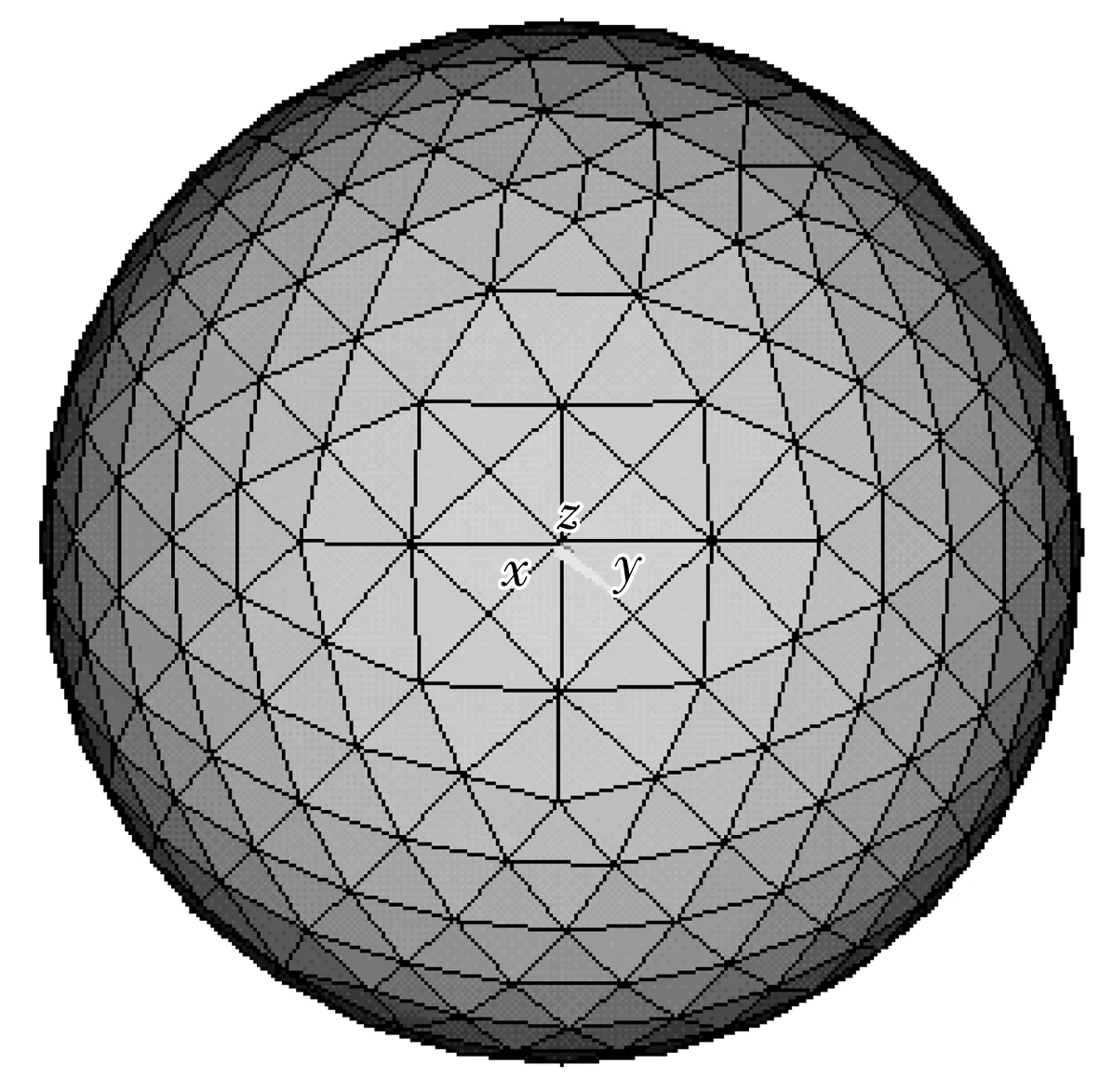
图3 三角形网格划分示意图
2 仿真结果与讨论
2.1 沟槽半径的影响
在双自转研磨装置加工范围内选取仿真参数(表2),下内、外盘转速的“三角波”转速曲线如图4所示,文献[3]已经验证了“三角波”转速曲线条件可实现研磨轨迹在球面的全包络,并且研磨均匀性较好。各种球半径rb在不同沟槽半径R下的球体研磨均匀性标准差S如图5所示。

表2 球半径与沟槽半径尺寸配比仿真参数
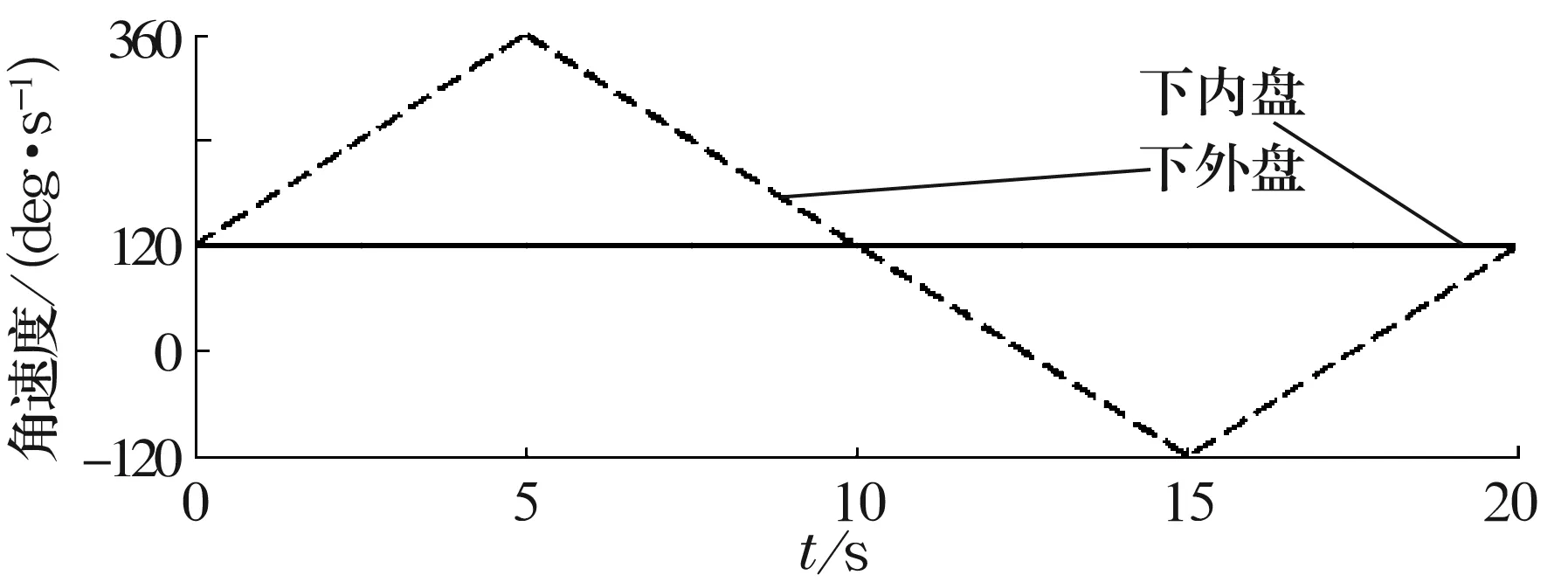
图4 研磨盘转速“三角波”曲线图
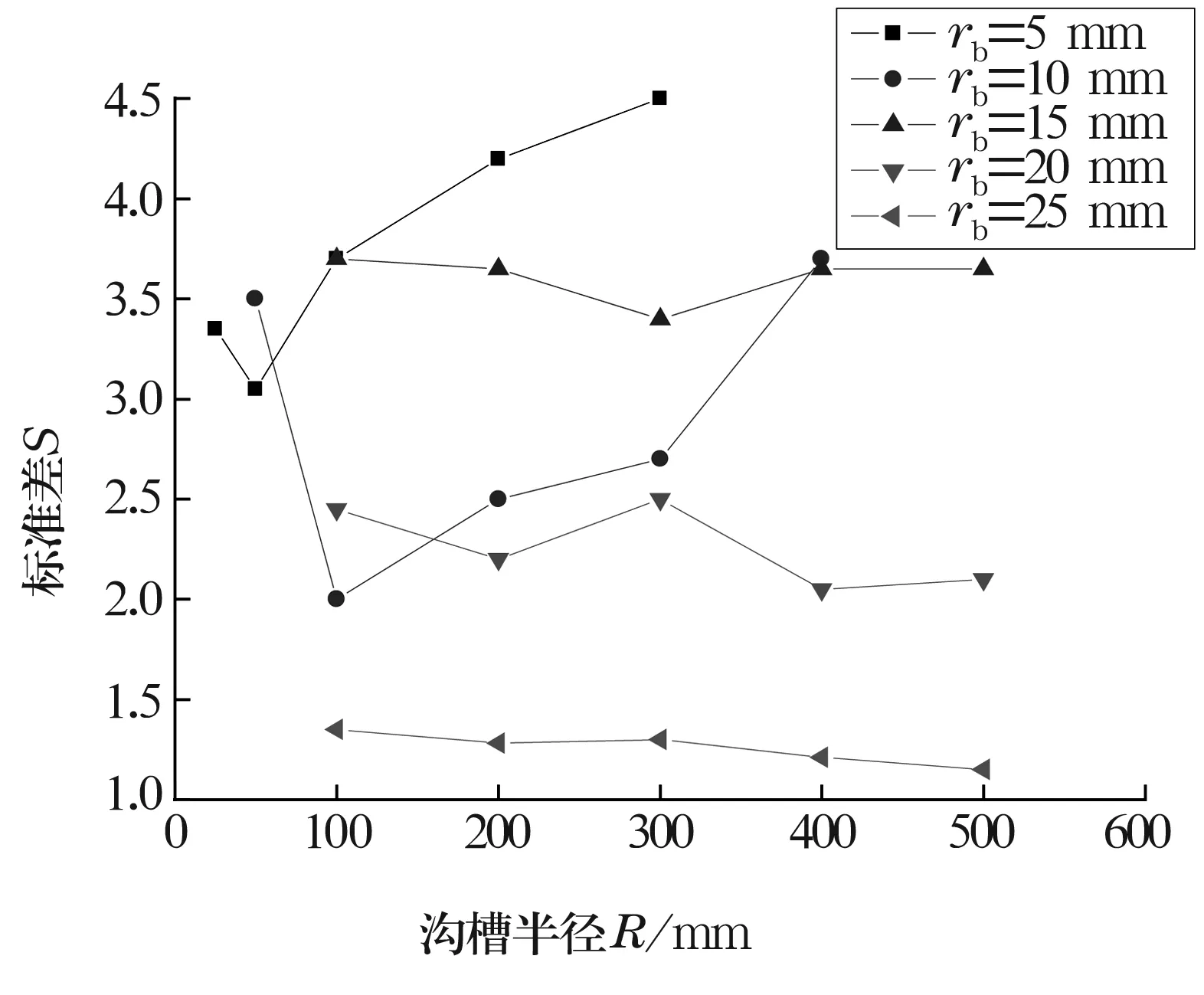
图5 沟槽半径R和球半径rb不同配比时的研磨
由图可知,当rb<15 mm,R与rb尺寸配比为10∶1时,标准差S最小;当15 mm≤rb≤25 mm ,R与rb尺寸配比为20∶1时,标准差S最小。
2.2 沟槽角度的影响
对不同沟槽角度下双自转研磨成球过程进行仿真研究,仿真条件为:球半径rb=20 mm,沟槽半径R=400 mm;沟槽角度α取15°~75°。仿真研磨中研磨盘转速仍采用“三角波”曲线。
在不同沟槽角度(15°,30°,45°,60°,75°)下研磨均匀性标准差S的变化如图6所示。由图可知,沟槽角度为45°~60°时,标准差S较小。在实际加工中,沟槽角度一般取45°为最佳。
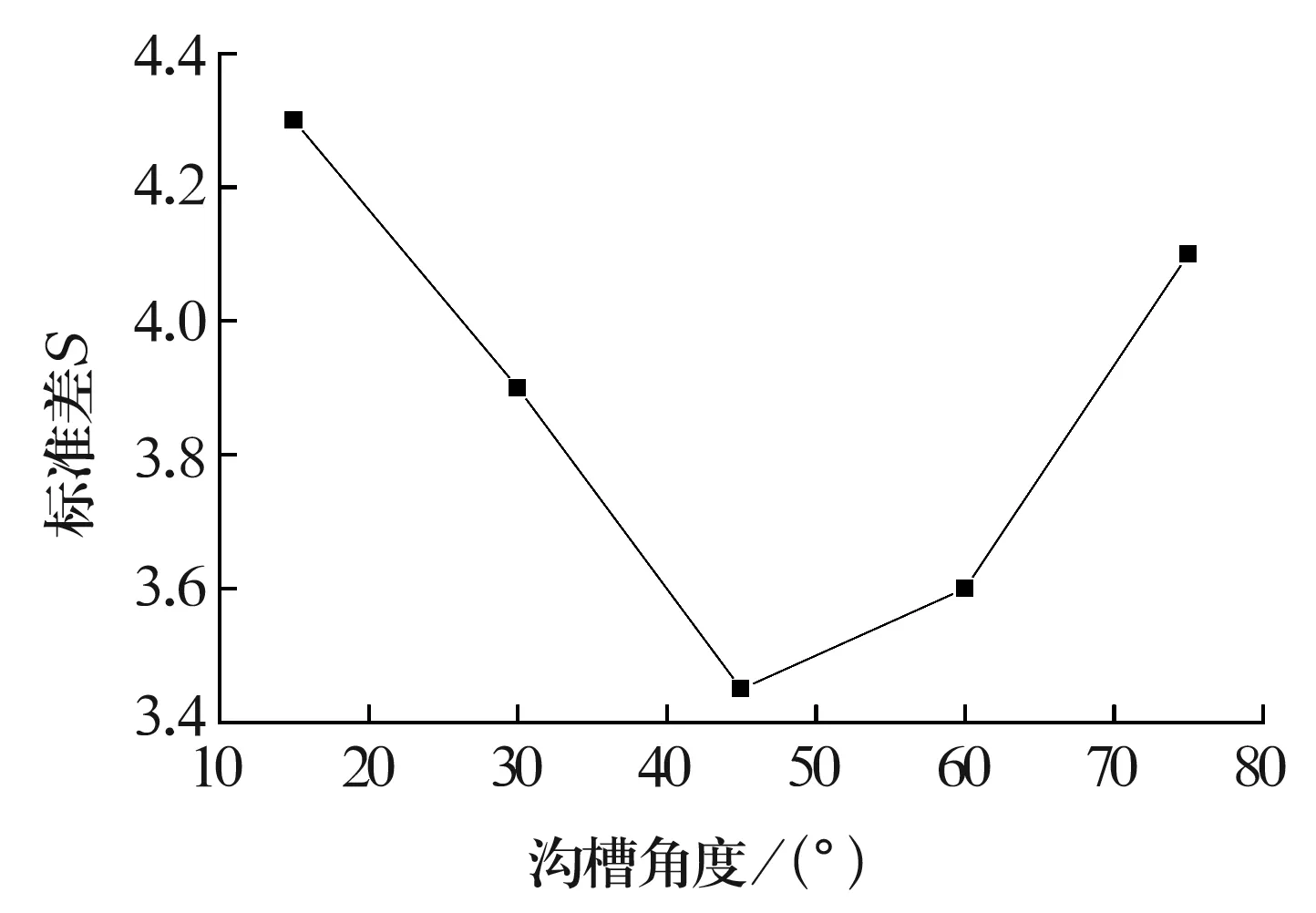
图6 研磨盘沟槽角度对研磨均匀性的影响
3 试验验证
根据仿真结果可知,最佳沟槽角度为45°,球半径为10 mm,R与rb配比为10∶1,即研磨盘沟槽半径R为100 mm时最佳。因此采用对比验证法,对双自转研磨方式不同研磨盘结构参数下球体加工后的球形误差进行测量。试验条件见表3。加工设备为Olymball-D600,磨料为B4C(粒度W3.5,质量分数10%),研磨盘为铸铁盘,球半径rb=10 mm,加工载荷(每球)为1.5 N,研磨液为煤油,试验时间T=180 min(每60 min停机观察修整后再继续),球形误差的测量采用MMQ400型接触式圆度测量仪。
3组试验每组抽测9粒球,取球形误差平均值,测量结果见表3。由表3可知,采用仿真取得的最佳研磨盘参数加工的球体的平均球形误差最好。

表3 3种试验条件下球形误差平均值
4 结束语
基于ADAMS建立了双自转研磨方式下的数值仿真模型,利用此模型对下研磨盘结构对精密球体研磨均匀性的影响进行仿真分析,着重讨论了球半径与研磨盘沟槽半径的尺寸配比和沟槽角度对研磨均匀性的影响,仿真结果表明:当球半径为5~15 mm时,沟槽半径与球半径尺寸配比为10:1时研磨均匀性最好;当球半径为15~25 mm时,沟槽半径与球半径尺寸配比为20:1时研磨均匀性最好;沟槽角度宜取45°~ 60°,最佳参数为45°。试验结果与仿真结果的变化趋势一致,验证了仿真结果的正确性。

