轴向受载高速角接触球轴承的动态特性求解方法

于晓凯，刘凯歌 ，赵春江，孙北奇，谢鹏飞

(1．洛阳轴研科技股份有限公司，河南 洛阳 471039；2．太原科技大学，太原 030024)

高速电动机等高速旋转机械主轴中常采用的高速角接触球轴承承受的径向力与轴向力相比很小，因此，轴承受力模型可以简化为纯轴向受载模型。高速角接触球轴承的动态特性如接触角、轴向变形量和刚度会影响高速旋转机械的性能；因此计算不同轴向力下高速角接触球轴承的实际接触角、轴向变形量和轴向刚度意义重大。其计算方法通常采用Harris方法，但这种方法需要求解非常复杂的非线性方程，直接求解很困难[1]，计算精度也很难达到要求。文中将实际接触角设定为迭代基本变量，分析高速角接触球轴承轴向受力工况下的动态方程组，将非线性方程组的参数由原来的7个减少为2个，简化了计算。

1 求解方程的简化

求解角接触球轴承的动态特性需要从接触变形入手，建立轴承的几何方程、变形方程、球平衡方程、套圈平衡方程，包括6Z+2(Z为球数)个方程，再建立包括离心力、陀螺力矩、接触角等在内的辅助方程组，应用Newton-Raphson 方法求解[2]。

由于纯轴向载荷下高速角接触球轴承只发生轴向变形，基于此建立变形方程。由于轴承承受纯轴向载荷时，各个球的受力情况相同，因此力平衡方程个数比较少，可对力平衡方程进行归一化处理。

仅轴向受载时，球心和沟道曲率中心位置变化关系如图1所示。根据承载前、后内、外沟道曲率中心距的径向分量不变，可得变形协调方程为

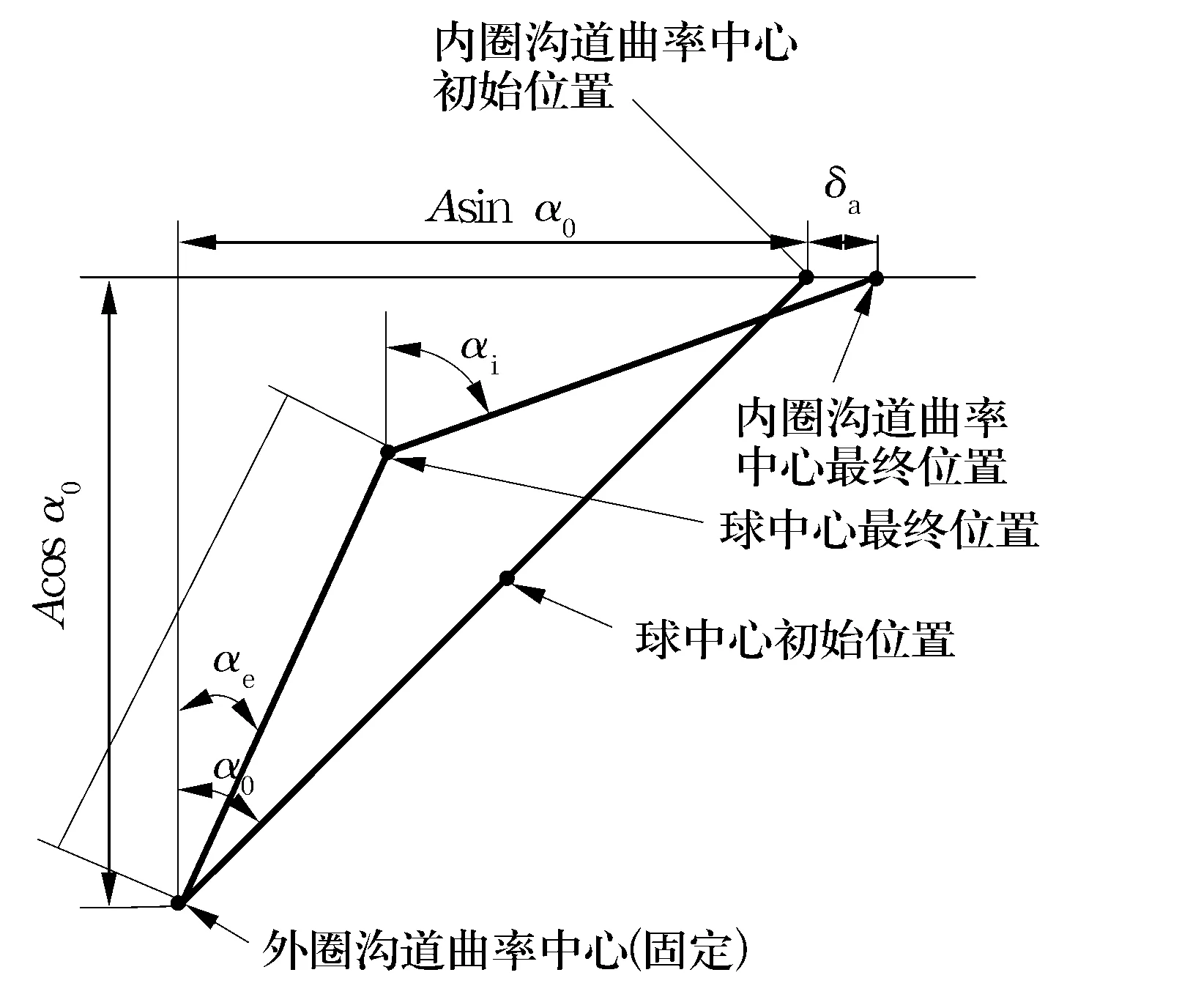
图1 球中心和沟道曲率中心位置

[(fe-0.5)Dw+δe]cosαe+[(fi-0.5)Dw+δi]cosαi=(fi+fe-1)Dwcosα0，

(1)

式中：fi，fe分别为内、外沟曲率半径系数；Dw为球直径，mm；δi,δe为球与内、外圈间的弹性变形量，mm，αi，αe为球与内、外圈间的实际接触角，(°)；α0为原始接触角，(°)。

因为陀螺力矩对实际内、外接触角的影响很小，所以以实际内、外接触角为迭代基本变量的求解方法中，可以忽略陀螺力矩的影响。故球所受到的载荷可以仅考虑与内、外圈间的接触载荷以及自身的离心力，如图2所示。

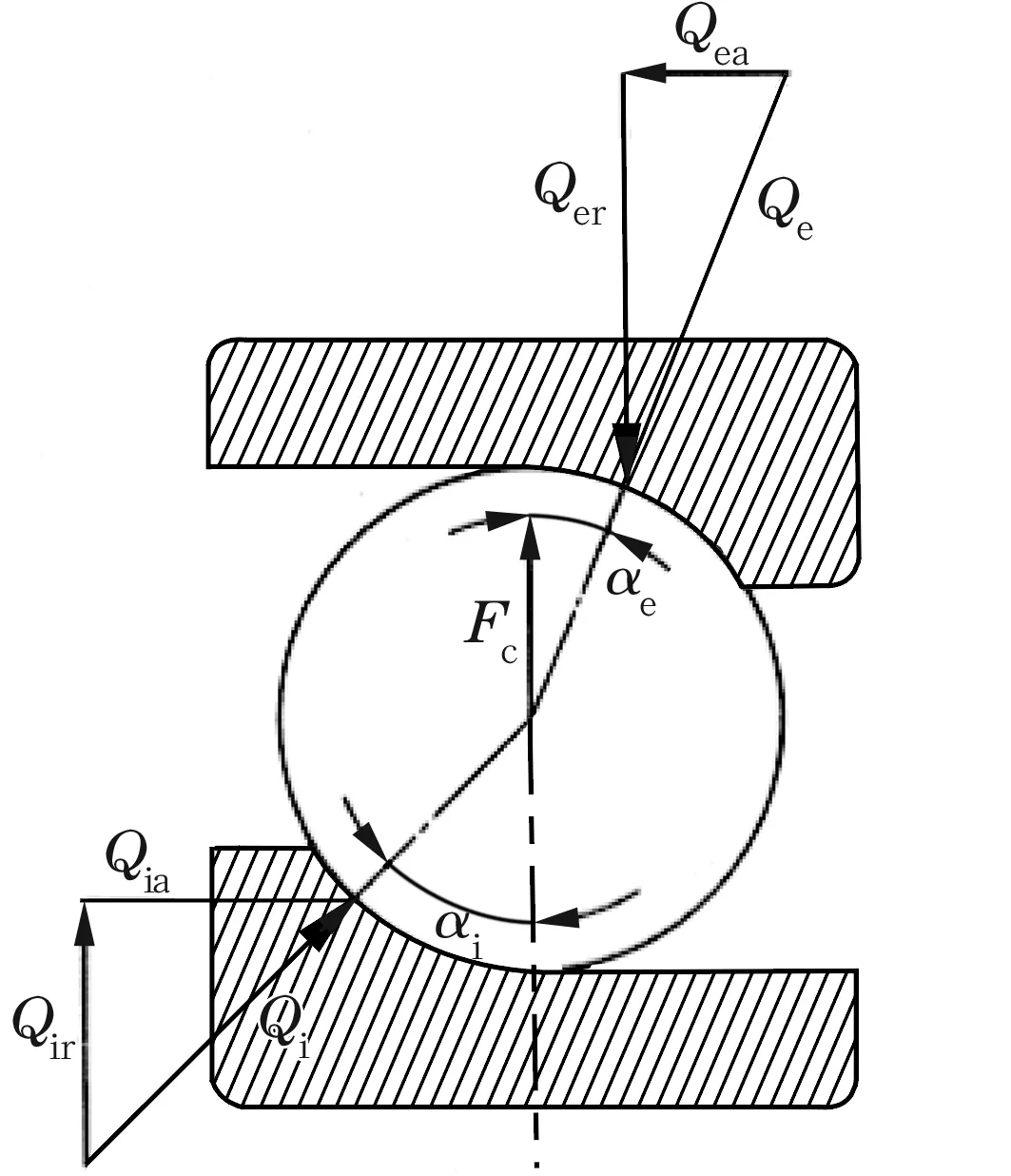
图2 离心力作用下球的受力图

根据球的受力关系，可知

(2)

式中：Fa为轴承受到的轴向力，N；Z为球数；Qia，Qea为球与内、外圈间接触载荷的轴向分量。

球与内、外圈的接触载荷为

(3)

(4)

球与内、外圈间接触载荷的径向分量为

(5)

(6)

由于球径向受力平衡，则

Qir+Fc=Qer，

(7)

式中:Fc为球所受的离心力，N。

将(5)～(6)式代入(7)式，得力平衡方程为

(8)

球轴承的接触载荷与接触变形间的关系为

(9)

(10)

式中：Ki，Ke为球与内、外圈间的载荷-变形常数，N/mm1.5。

将(3)～(4)式分别代入(9)～(10)式，可得

(11)

(12)

将(11)和(12)式代入(1)式，可得

(13)

联立(8)式和(13)式即得实际接触角的求解方程组。通过求解方程组，可得高速角接触球轴承的实际接触角αi,αe，从而通过图1所示的球中心和沟道曲率中心位置关系得到轴承的轴向位移量δa为

δa=[(fe-0.5)Dw+δe]sinαe+[(fi-

0.5)Dw+δi]sinαi-(fi+fe-1)·

Dwsinα0。

(14)

2 求解方程的基本变量分析

根据轴承的动态求解方程组，分析其中的基本变量[3]。离心力方程为

(15)

式中：Dpw为球组节圆直径，mm；nm为球公转速度,r/min。球的公转速度nm为

(16)

根据外沟道控制理论假设

(17)

(18)

式中：内、外圈旋转方向相反时取“-”，相同时取“+”；Ω为套圈角速度,rad/s；β为球姿态角,(°)；γ为几何参数。

接触变形常数K为

K=2.15×105(∑ρ)-1/2nδ-3/2，

(19)

式中：nδ为接触变形系数，可以根据主曲率差函数F(ρ)查表求得；∑ρ为主曲率和函数，mm-1。

根据(15)～(19)式，依次寻找离心力、接触载荷变形常数与内、外接触角的关系，如图3所示，图中箭头左边是箭头右边的函数。

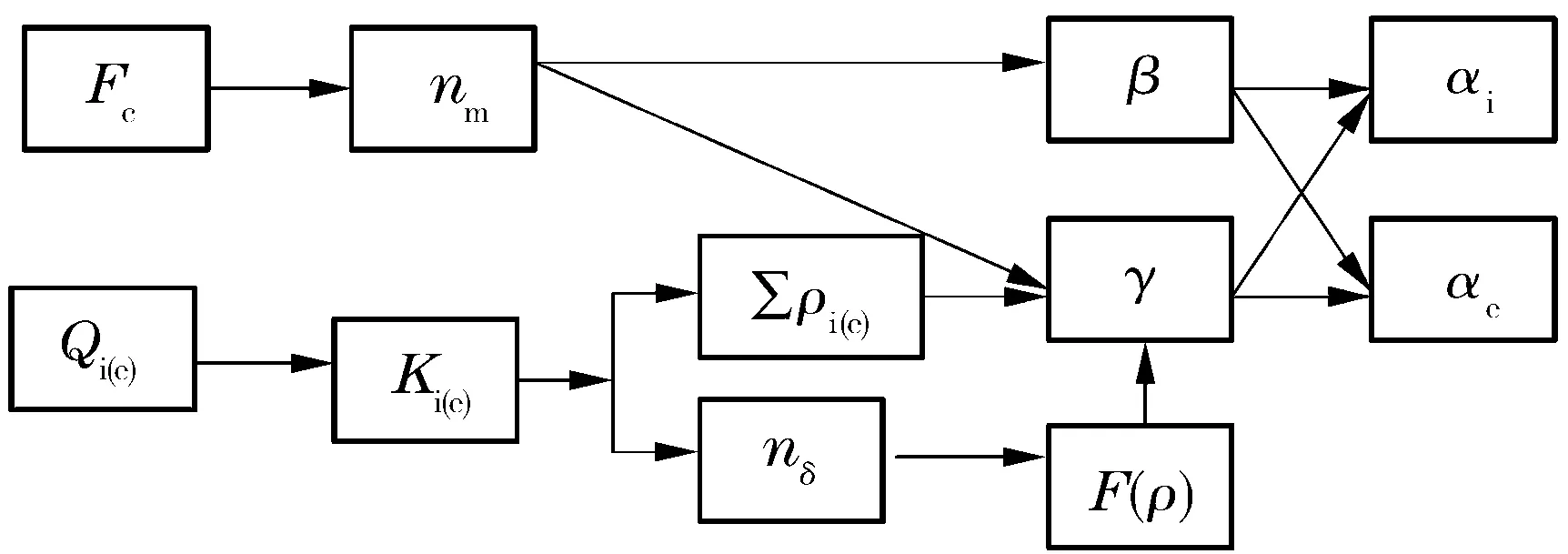
图3 变量传递关系

3 求解步骤及算例

纯轴向载荷下高速角接触球轴承上述方程组的求解流程如图4所示。求解过程中，采用全局收敛算法(Broyden算法)。

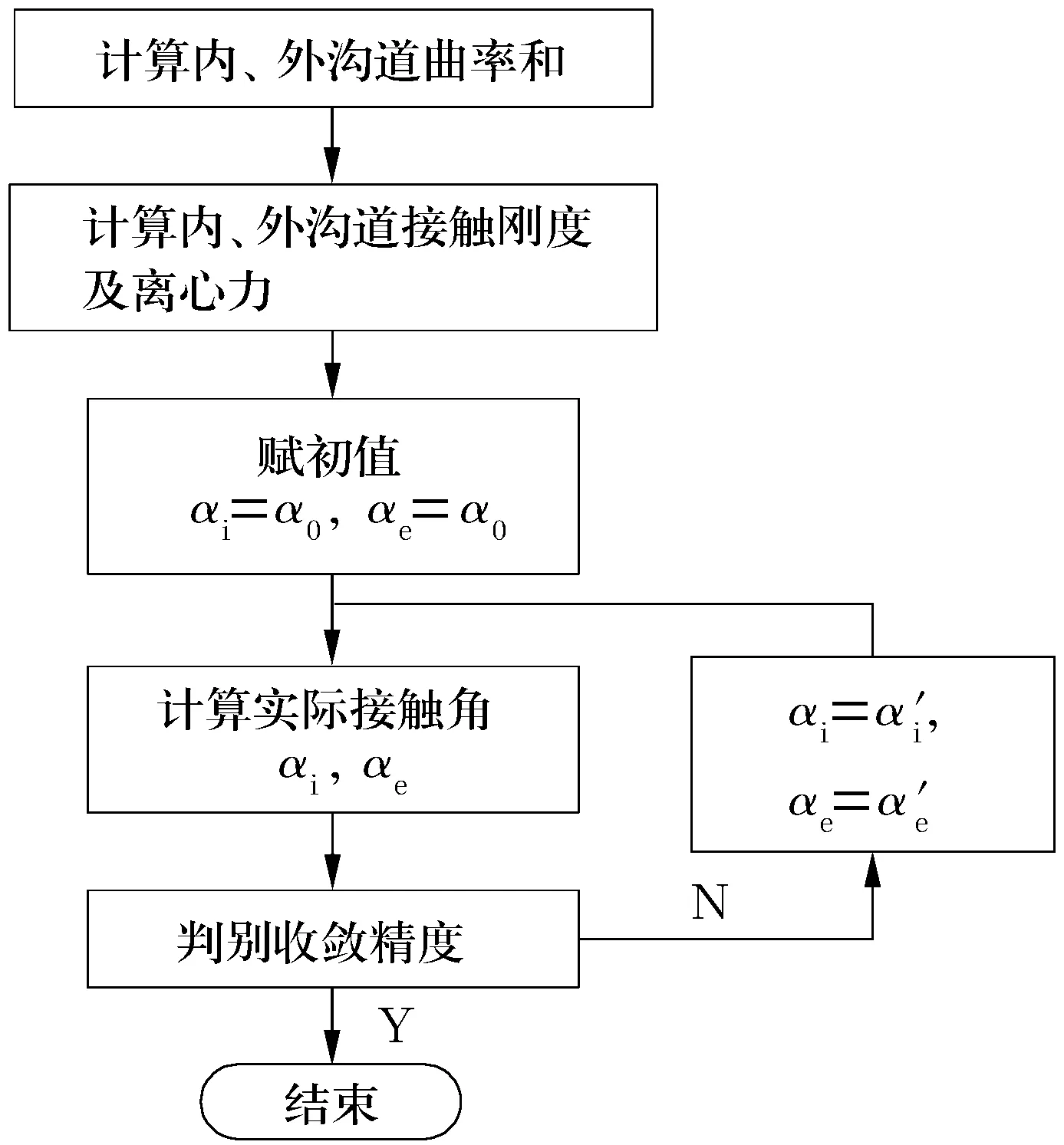
图4 计算流程图

利用文中给出的计算方法对7218B角接触球轴承在给定的受力和转速情况下进行编程计算，得到表1所示的计算结果。7218B角接触球轴承的几何参数为Dw=22.23 mm,Dpw=125.26 mm，fi=fe=0.523 2，Z=16,α0=40°。由表1可知，采用文中的方法与Harris的方法得到的结果相差不大，充分说明了基于接触角迭代方法求解纯轴向受力的高速角接触球轴承动态特性的可行性[3]。

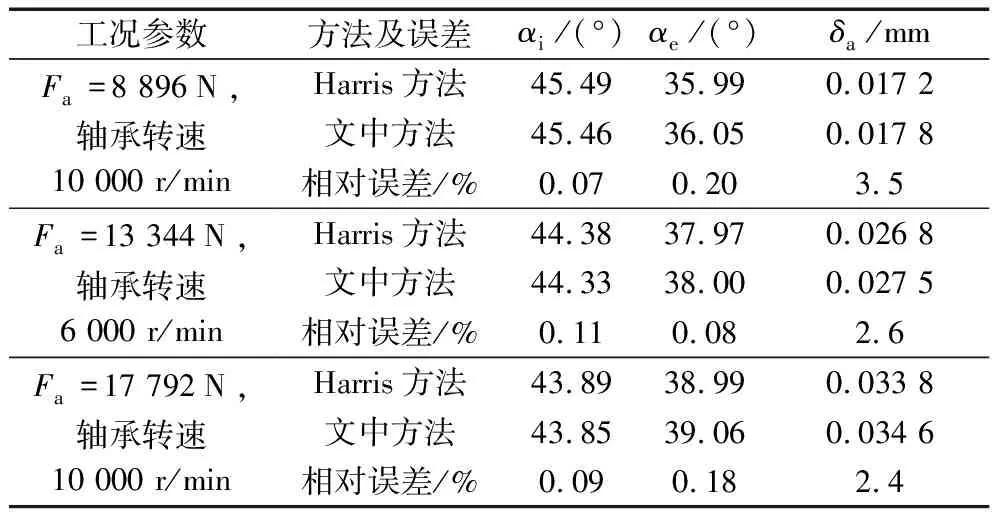
表1 不同工况下的计算结果

4 结束语

依据纯轴向受力的高速角接触球轴承的特点，建立了轴承的变形协调方程和力平衡方程，基于实际接触角对方程组进行迭代求解，求解结果与Harris方法的计算结果比较吻合，说明了该计算方法的有效性，同时，新计算方法中求解参数比Harris方法减少了一半，计算量较小。