基于ANSYS的双曲面斜滚子轴承离合器应力分析

李蕾，孙东辉，毕超

(沈阳航空航天大学 机电工程学院，沈阳 110136)

双曲面斜滚子轴承离合器是一种靠摩擦力传递力矩的新型离合器，与普通的离合器相比具有结构紧凑、承载能力高、楔紧可靠和寿命长等优点[1]，被应用于工业自动化、航天等领域，具有广泛的应用前景。

双曲面斜滚子轴承离合器内、外圈与滚子接触的工作面是标准单叶双曲回转面等距曲面[2]，滚子与内、外滚道的三维曲线接触问题属于非线性接触问题。由于接触力的大小对离合器的总体性能有着重要影响，因此其接触问题的研究显得尤为重要。文中从双曲面斜滚子轴承离合器工作原理入手，根据滚子与内、外圈接触曲线方程，采用UG建立内、外圈单叶双曲面等距曲面的三维模型，再导入ANSYS软件，利用其接触分析的强大功能，尽可能真实地模拟离合器工况进行接触分析，以期达到对此种新型离合器的全三维应力分析，同时分析了离合器不同的结构参数对等效应力的影响。

1 工作原理

双曲面斜滚子轴承离合器结构如图1所示。它由内圈、外圈、滚子和保持架组成。滚子轴线系单叶双曲回转面上的一条直线，如图2所示，内、外圈与滚子接触的工作面是标准单叶双曲回转面等距曲面，滚子与内、外圈形成空间曲线接触[3]。单叶双曲回转面是由一条直素线(即滚子轴线)绕内、外圈轴线旋转而成[4]。滚子轴线同内、外圈轴线为空间异面直线，空间夹角为β，在双曲面上截取一部分曲面作为保持架的形状曲面，曲面的形状参数用所截取曲面的轴向位置Zc表示。

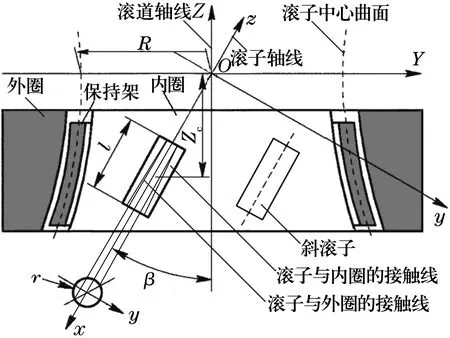
图1 双曲面斜滚子轴承离合器结构

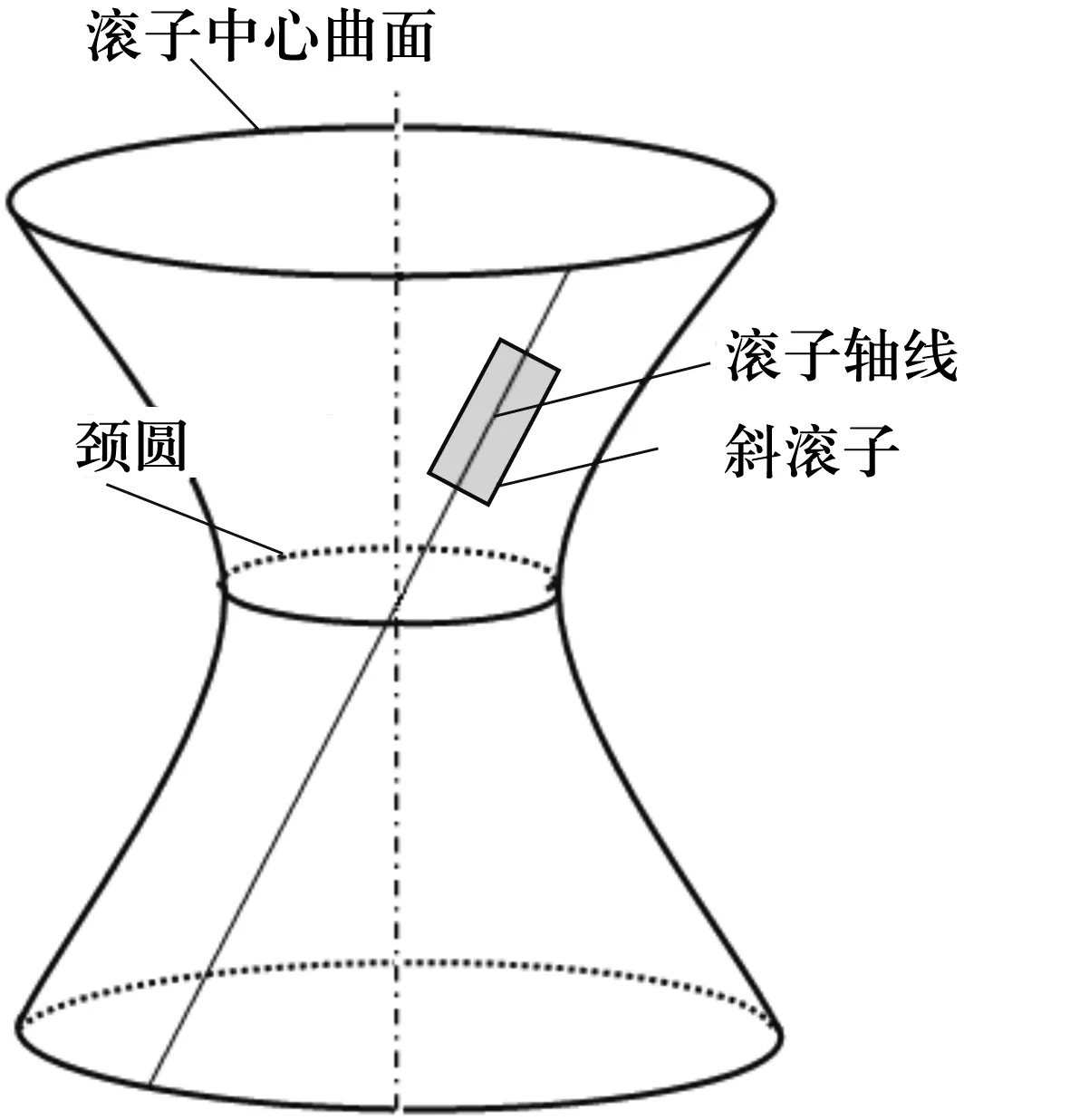
图2 滚子轴线所在单叶双曲面

双曲面斜滚子轴承离合器可以是外圈做主动件，内圈做从动件；也可以是内圈做主动件，外圈做从动件。以下分析假设内圈为主动件，外圈为从动件。根据不同的设计参数，工作时分如下两种工况。

(1)轴向载荷控制主动件与从动件的离合。离合器工作时，内圈逆时针(从上往下看)转动的同时滚子既绕自身的轴线自转又绕离合器的轴线公转。当施加给内圈一轴向力时，滚子与滚道间将产生法向接触力，由于滚子轴线与滚道轴线有一空间夹角β，所以滚子在做自转和公转的同时又必将沿着自身的轴线方向进行滑动，使接触表面产生摩擦力，因而在这种滚滑摩擦状态下产生的摩擦力矩使内圈传递转矩带动外圈转动[5]。离合器的楔合或脱开类似于单向超越离合器的超越功能，依靠主、从动部分相对转动速度的变化实现。当外圈转速超越内圈转速时，离合器脱开，内圈和外圈分别以各自的速度转动；否则，离合器楔紧，内圈、外圈和滚子一起转动。

(2)靠自锁控制主动件与从动件的离合。与锥螺纹拧紧过程相似，它是以一定螺旋角排列的滚子替代锥螺纹的螺牙[1]，滚子在内、外圈滚道上呈右旋排列时，在一定的轴向预紧力下，当内圈在扭矩的作用下逆时针(从上往下看)转动时，由于内、外圈与滚子3者中只有内圈可沿着轴线方向向上移动，致使内、外圈之间的法向间距减小，当滚子上压力增大到一定程度而楔紧即产生自锁，此时内、外圈与滚子可看成一体，并以相同的角速度转动，仅通过滑动静摩擦力的作用传递转矩。与此相反，当内圈相对于外圈顺时针方向转动时，内圈沿轴向向下移动，内、外圈之间法向间距变大，滚子自由转动，此时离合器脱开。若滚子在内、外圈滚道中呈左旋排列时，则与上述运动情况相反，内圈顺时针方向转动时离合器楔紧，逆时针方向转动时脱开。文中选取第2种工况，对离合器自锁状态下的接触应力进行数值模拟分析。

2 滚子与内、外圈工作面接触分析

2.1 接触对类型分析

从材料屈服的角度看，滚子与滚道曲面接触形成的最大Von Mises等效应力限制了斜滚子离合器所能传递的极限力矩，而斜滚子离合器只有在楔紧状态下方能传递扭矩。研究离合器的接触应力问题，即对楔紧过程中滚子与内、外圈滚道间接触面区域的接触应力及整体Von Mises等效应力进行分析。在该离合器中，由于滚子与滚道材料的硬度相近，两个接触体都是变形体(假设刚度相同)，故可将问题归结为柔体与柔体的面面接触问题。

2.2 有限元模型的建立及简化

在图1所示OXYZ坐标系下，滚子与内、外圈接触的三维曲线方程为[6]

式中：l为滚子的长度；r为滚子半径；R为滚子中心双曲面颈圆半径；下标i和e分别表示滚子与内、外圈的接触曲线。

根据接触曲线方程，用UG中的表达式功能建立内、外接触曲线，分别将内、外接触曲线绕离合器的轴线旋转一周即形成内、外圈的工作曲面。结合所选取的计算模型参数：滚子半径r=3 mm，滚子长度l=20 mm，滚子个数Z=12，内圈孔直径d=45 mm，外圈直径D=96 mm，滚子轴线与内、外圈滚道轴线之间夹角β=30°，滚子中心双曲面颈圆半径R=33 mm，滚道曲面的轴向位置Zc=17.5 mm。利用UG强大的曲线曲面造型功能建立三维模型，如图3所示，模型中忽略倒角和滚子的修形。采用parasolid格式，将其导入ANSYS中。

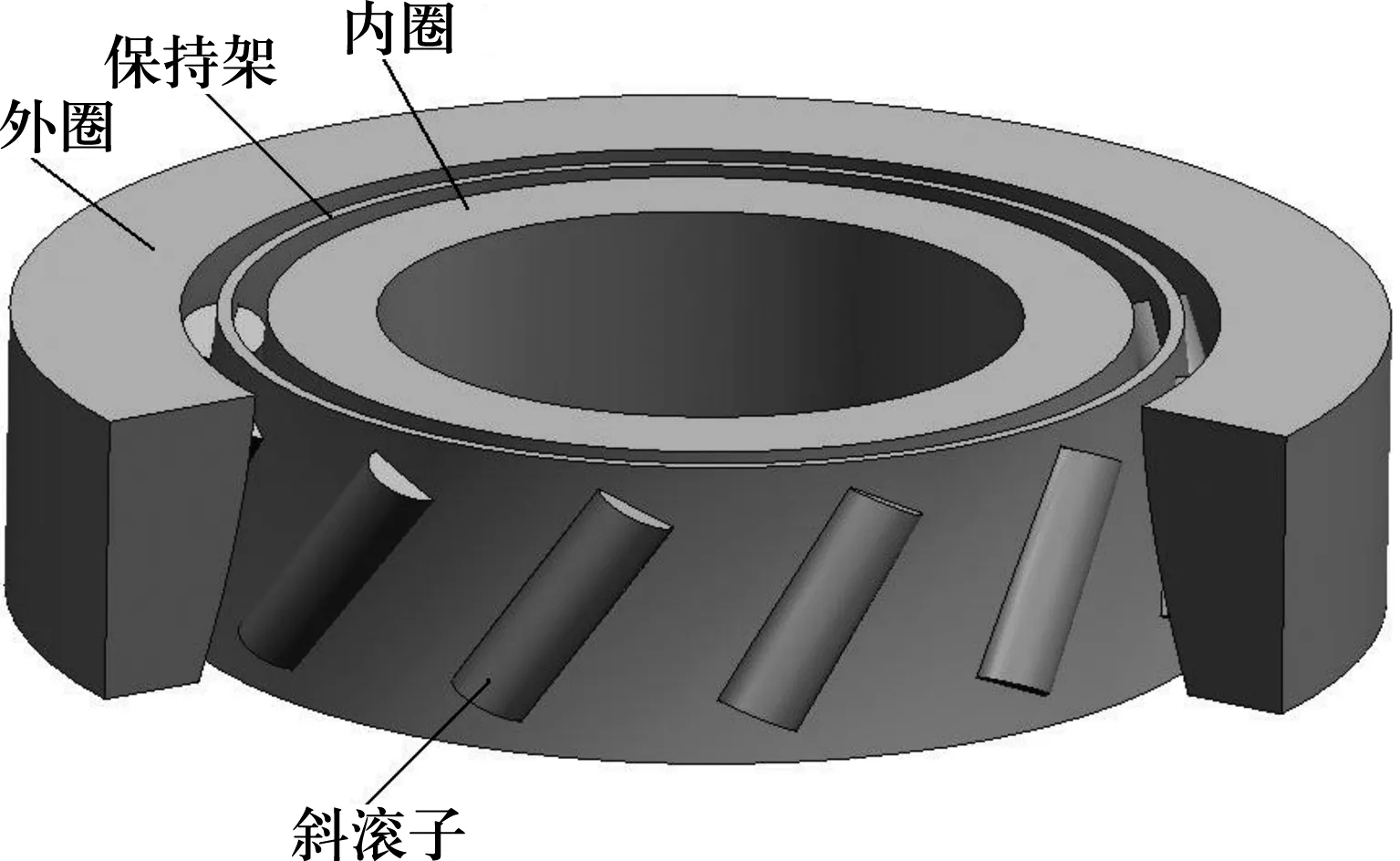
图3 双曲面斜滚子轴承离合器实体模型

考虑到离合器结构的对称性和受力特点，为简化计算，进行轴对称处理，截取整圈的1/12进行分析。滚子和内、外圈材料均选用轴承钢G20Cr2Ni4，弹性模量为206 GPa，泊松比为0.3。计算单元选择Solid 186(3维20节点六面体等参实体单元)，整体有限元模型网格划分方式采用智能网格(4级SmartSize)，对滚子与内、外圈接触区域进行局部细化，细化网格尺寸小于接触椭圆短半轴尺寸的50%为宜[7]，划分后共有100 427个单元，132 095个节点。图4为简化后的网格划分模型。接触单元用Contact 3D Target 170模拟内、外圈滚道表面，用Contact 8nd surf 174模拟圆柱滚子的外表面。分别定义滚子与内、外圈之间的接触对，摩擦因数(钢与钢)取0.1，设置法向接触刚度因子FKN=0.5，切向接触刚度FKT=1.0，最大渗透容差FTOLN=0.1，初始闭合因子ICON=0.01，选取非对称刚度矩阵Unsymmetric。图5所示为定义的接触对图。

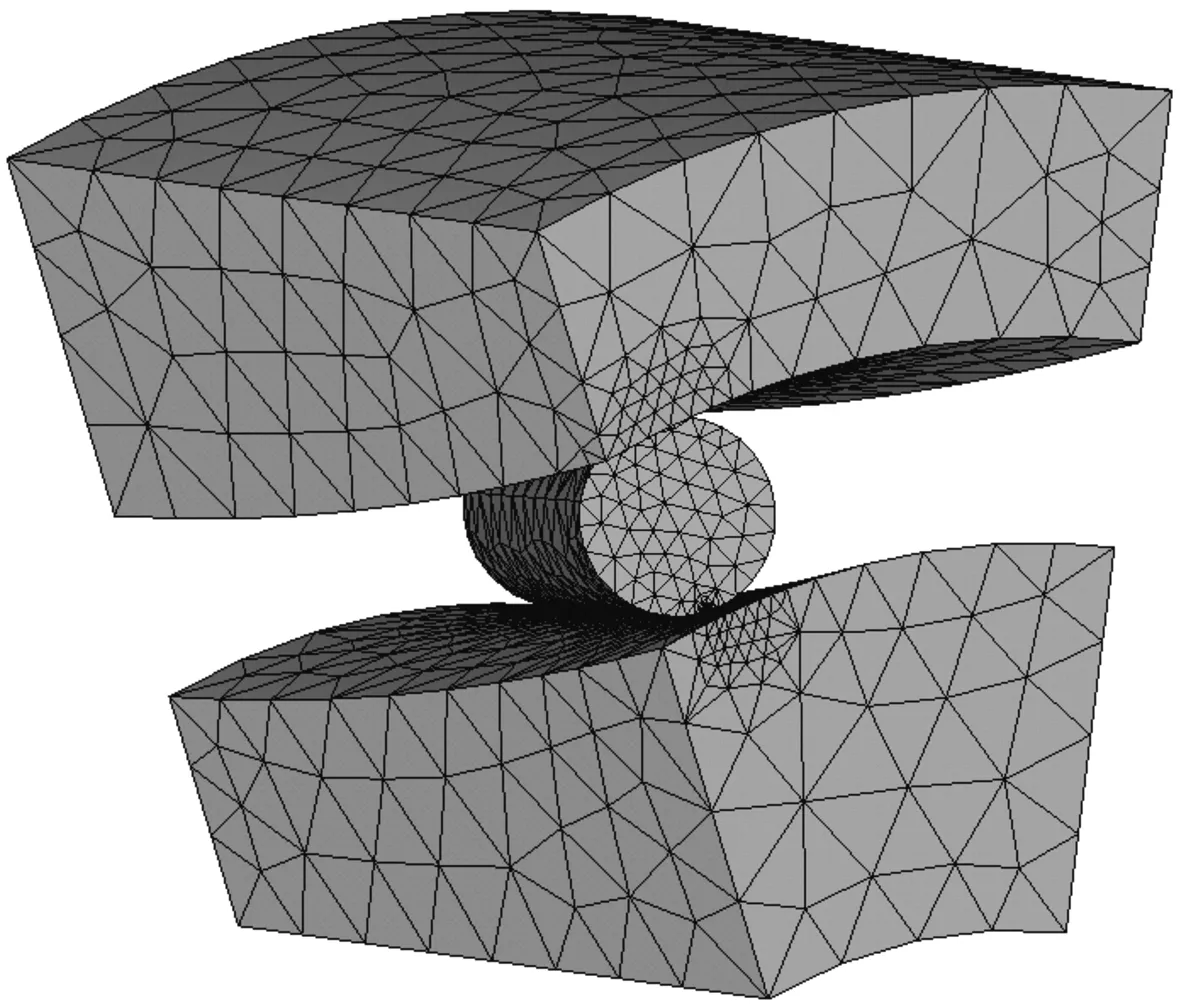
图4 网格划分模型

图5 接触对

2.3 约束条件、施加载荷与求解

保持架的模拟可简化为：把滚子外表面节点转换到以滚子中心为原点创建的局部柱坐标系下，并约束这些节点的切向(UY)位移。外圈侧面约束其UZ向的位移，耦合内圈内表面上所有节点的径向(UX)及周向(UY)的自由度，使得在轴向载荷下能保持内圈内表面的刚性。为了定性地分析结构参数对等效应力的影响规律，在进行ANSYS分析时，考虑到调整模型结构参数可能出现最大等效应力大于材料许用极限应力的情况，故在外圈外表面施加数值较小的均布面载荷P(P=500 Pa)。同时内圈施加轴向位移UZ(UZ=8 μm)，截面处施加对称自由度约束。约束条件及施加的载荷如图6所示。

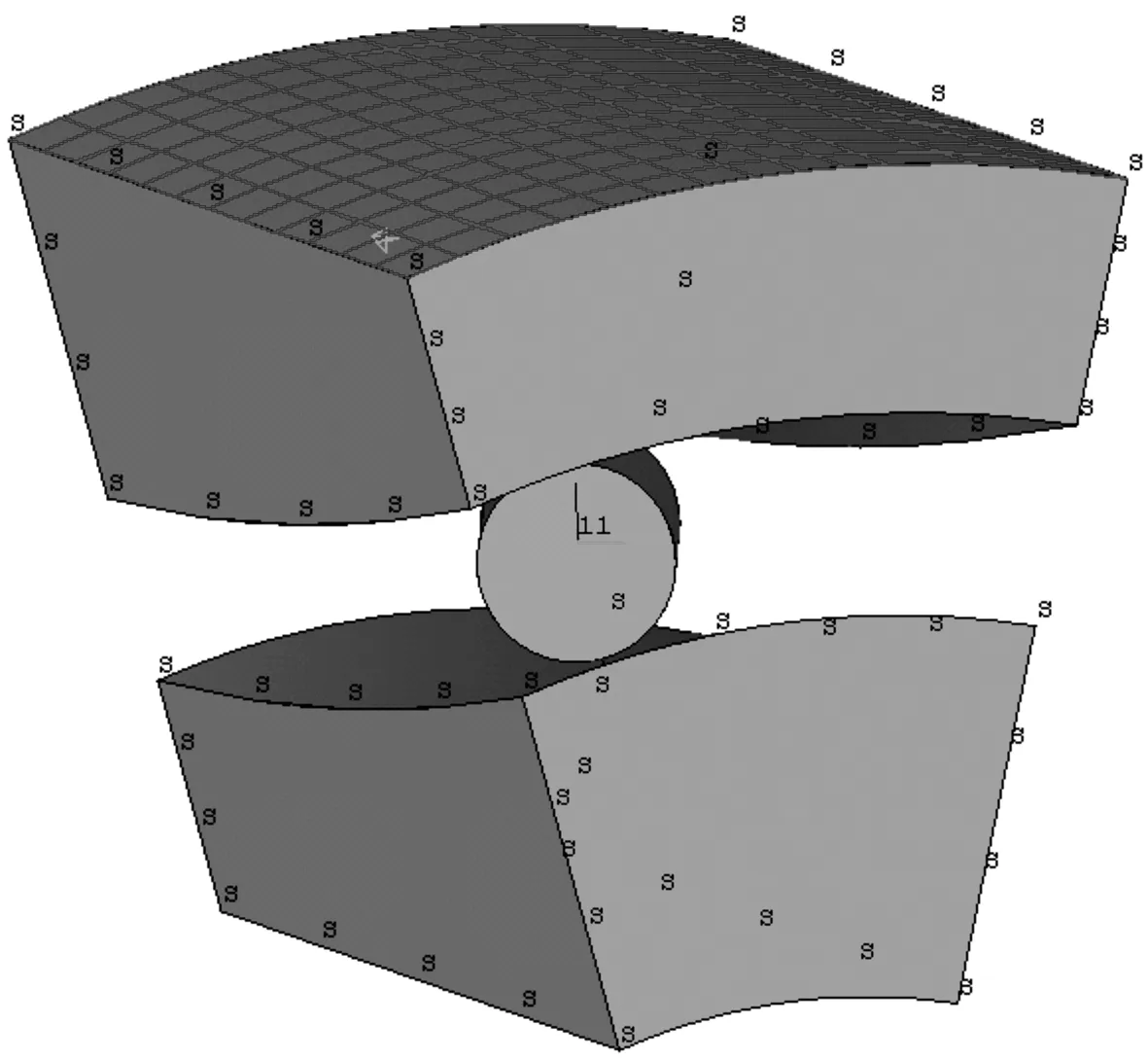
图6 约束与加载

打开自动时间步长，设定子载荷步数为 10，最大子步数为 100，最小子步数为 1，打开预测器使用线性搜索来加强非线性迭代的收敛，然后进行非线性分析，计算结果收敛。由分析结果可以看出，在外载荷作用下，接触面单元的接触应力分布如图7所示，最大接触应力值为173 MPa。

在相同工况条件下，采用Hertz理论[8]简化力学模型得出最大接触应力值为204.4MPa。该结果表明，有限元数值计算与理论分析结果存在的误差在工程容许的范围内，且数值计算方法更为方便有效。图8为Von Mises等效应力放大图；图9为滚子与内、外圈接触时滚子的Von Mises等效应力云图；图10、图11分别为内、外圈的Von Mises等效应力云图；图12为扩展下的整体等效应力云图，可以方便观察整体模型的应力状态。

3 结构参数对Von Mises等效应力的影响

结构参数β，r，l，Zc，R和Z的取值直接影响离合器所受应力的大小、承载能力及整体结构尺寸，选择合理的结构参数对提高离合器的使用性能和延长其使用寿命具有重要意义。

在相同模型和工况下，分析各结构参数对离合器Von Mises等效应力的影响。

当r=3 mm，l=20 mm，Zc=17.5 mm，R=33 mm，Z=12时，不同β角对应的最大等效应力如图13所示。由图可知，最大等效应力随β的增大而增大。

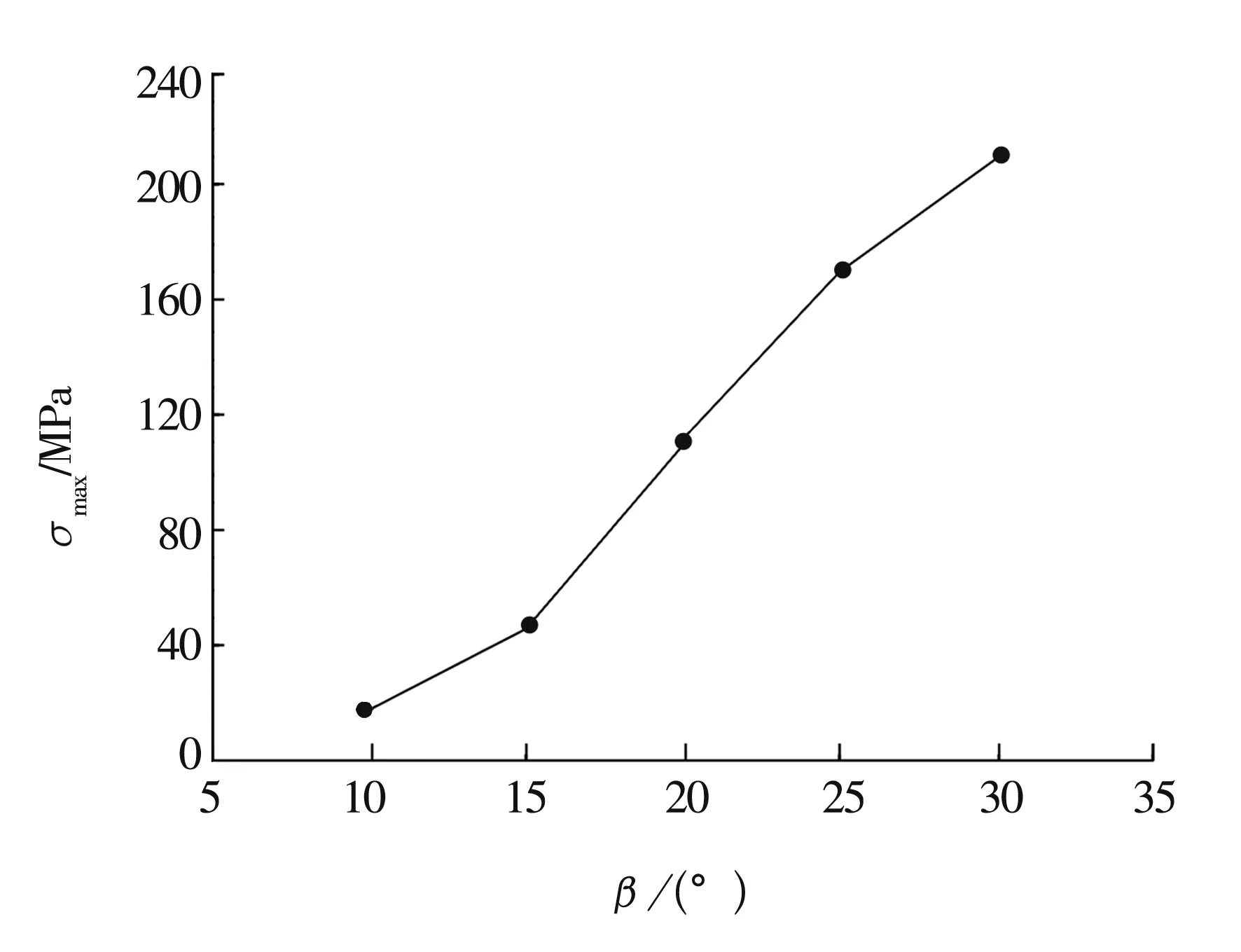
图13 最大等效应力随β的变化曲线

当β=30°，l=20 mm，Zc=17.5 mm，R=33 mm，Z=12时，不同的r对应的最大等效应力如图14所示。由图可知，最大等效应力随滚子半径r的增大而减小。

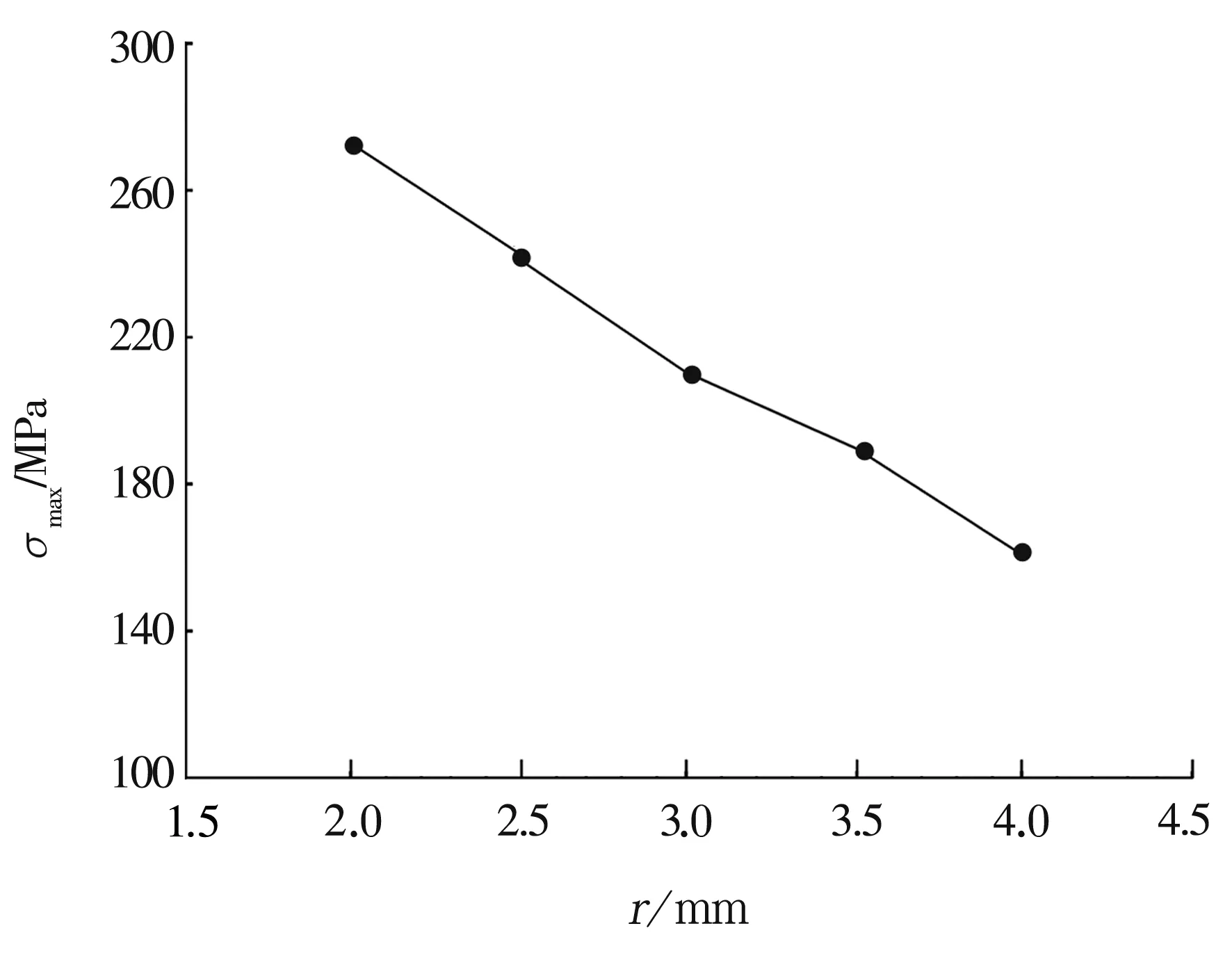
图14 最大等效应力随r的变化曲线

当β=30°，r=3 mm，Zc=17.5 mm，R=33 mm，Z=12时，不同的l对应的最大等效应力如图15所示。由图可知，最大等效应力随滚子长度l的增加而减小。

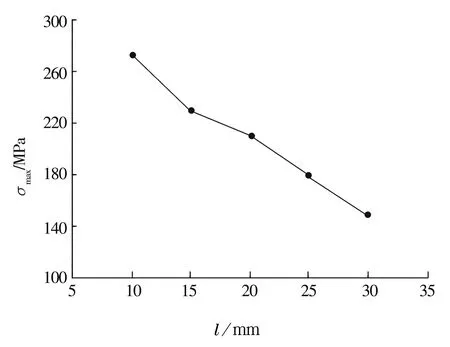
图15 最大等效应力随l的变化曲线

当β=30°，r=3 mm，l=20 mm，R=33 mm，Z=12时，不同的Zc对应的最大等效应力如图16所示。由图可知，最大等效应力随轴向位置尺寸Zc的增大而增大。

图16 最大等效应力随Zc的变化曲线

当β=30°，r=3 mm，l=20 mm，Zc=17.5 mm，Z=12时，不同的R对应的最大等效应力如图17所示。由图可知，最大等效应力随R的增大而减小。

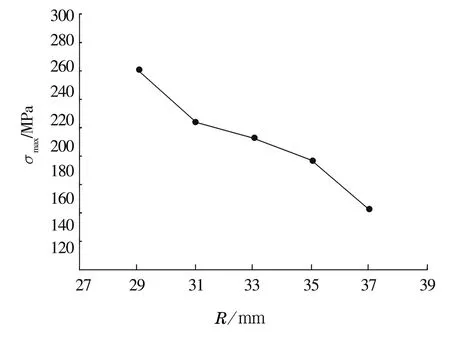
图17 最大等效应力随R的变化曲线

当β=10°，r=3 mm，l=20 mm，Zc=17.5 mm，R=33 mm时，不同的Z对应的最大等效应力如图18所示。由图可知，最大等效应力随滚子个数Z的增加而减小。

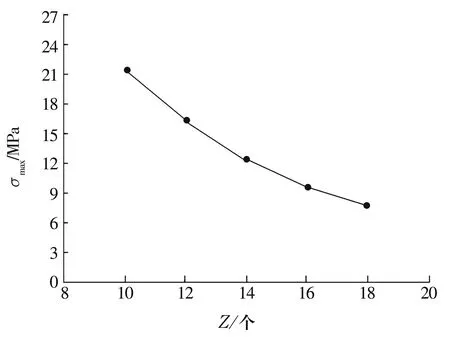
图18 最大等效应力随Z的变化曲线

4 结束语

(1)根据滚子与内、外圈接触的曲线方程，采用UG建立全三维接触模型，导入ANSYS对双曲面斜滚子轴承离合器的接触问题进行分析是一种行之有效的分析方法，可为产品结构的数字化设计提供较为实用的方法。

(2)滚子与内、外圈间接触的最大等效应力随β和Zc增大而增大；随r，R,l和Z的增大而减小。

(3)在离合器设计时，应综合考虑离合器的强度、离合性能和传动要求等，以降低最大Von Mises等效应力，提高离合器的使用性能，延长其使用寿命。