高转速对滚动轴承性能影响的分析与计算
刘良勇,李鸿亮,康正坡,徐海利
(洛阳轴研科技股份有限公司,河南 洛阳 471039)
随着各种工程技术的发展,旋转机械正在向更高转速、更高性能方向发展,转速动辄每分钟数万转,甚至每分钟数十万转,而作为转子支承的滚动轴承也必然向更高速方向发展。通常认为轴承的dm·N值大于1.0×106mm·r/min时为高速轴承。
高转速对轴承最直接的影响是轴承零件的惯性效应[1]。在离心力作用下钢球对外圈沟道接触应力增加,当与内圈沟道之间拖动力不足时钢球会发生公转打滑;在高速角接触球轴承中钢球高速旋转时由于其自转轴与公转轴之间存在一定夹角,当钢球与沟道接触区域的摩擦力不能平衡钢球自身的陀螺力矩时,钢球就会发生陀螺旋转。在高速轴承的设计与分析中通常都会考虑钢球的惯性效应即离心力和陀螺力矩,而其他零件的惯性效应则常常被忽略。轴承套圈和保持架在高速旋转时由于其惯性力作用,内、外径尺寸会发生变化,从而导致轴承的径向游隙(接触角)减小,进而导致轴承的性能发生变化;保持架与引导挡边之间的引导间隙减小进而引起保持架外径面与引导挡边之间产生摩擦磨损,甚至卡死。此外,保持架的强度、套圈的疲劳寿命与其内部的应力有密切关系[2],轴承的离心效应也会导致这些参数的改变。套圈和保持架均为圆环形零件,下文根据弹性力学理论推导了高速旋转圆环的内应力、位移与转速之间的关系,在此基础上分析了内圈转速对轴承性能的影响,并通过具体实例分析转速对轴承的径向游隙、引导间隙等参数的影响。
1 理论推导
极坐标系中,在径向平面内任一半径ρ处取一微小单元体,该微单元体的体积为单位体积,其受力情况如图1所示[3]。
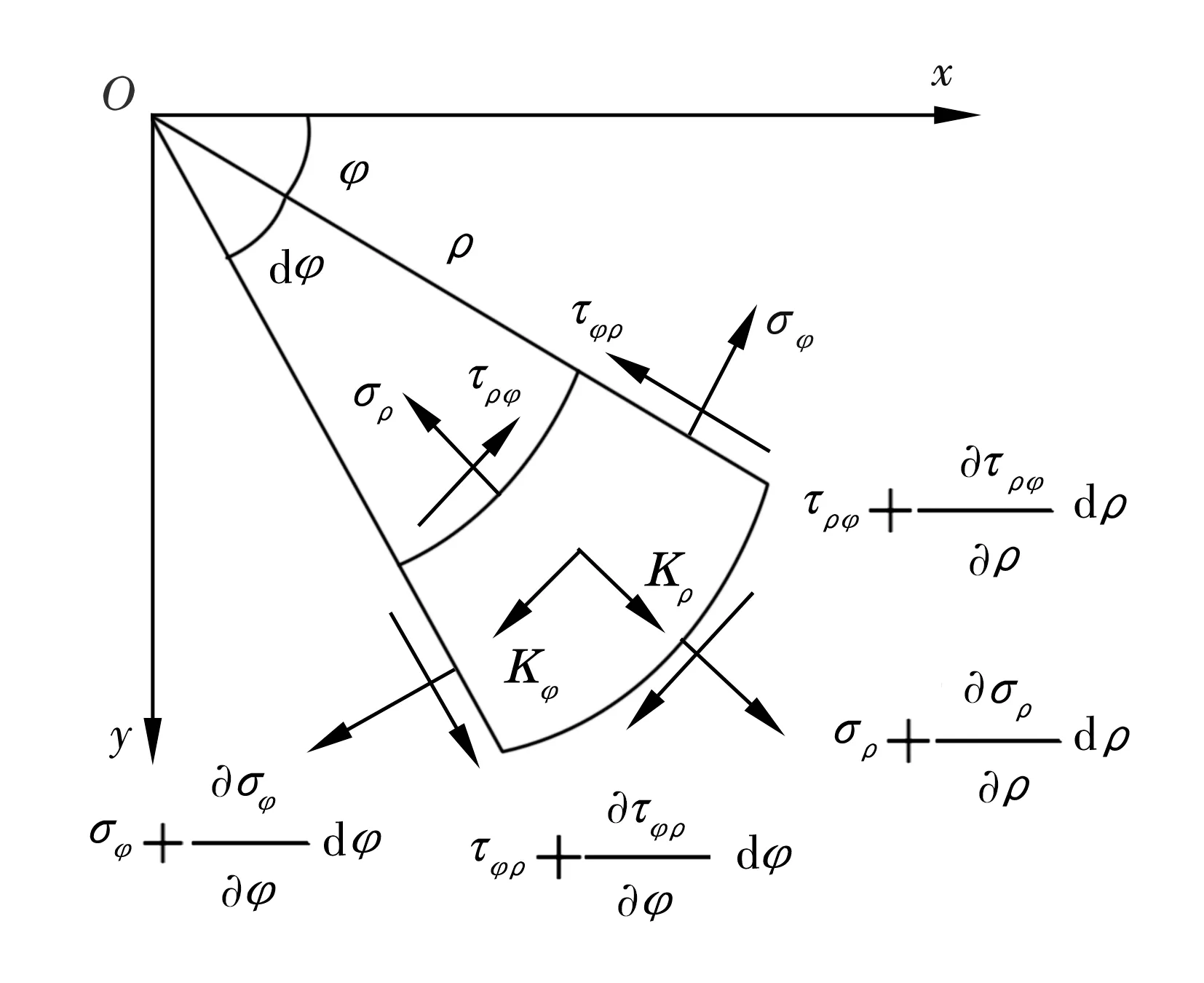
图1 极坐标下微单元应力
圆环以角速度ω旋转,其材料密度为p,弹性模量为E,泊松比为ν。则该单元体的离心力为
Kρ=pω2ρ。
若将单位体积的离心力作为径向的单位体积力作用在微单元上,根据达朗贝尔原理可以将微单元作为静力学问题来求解。由于旋转圆环属于轴对称问题,因此径向应力σρ和环向应力σφ均与极角φ无关,且切向应力满足τρφ=τφρ=0,于是图1中微单元径向力平衡微分方程为
(1)
由于圆盘中的位移分量也是轴对称的,即只有径向位移分量u(ρ),根据几何方程可得单元体的径向应变ερ和环向应变εφ
(2)
平面应力问题的应力和应变的物理方程为
(3)
将(2)式代入(3)式得
(4)
将(4)式代入平衡方程便可以得到用位移表示的平衡微分方程
(5)
(5)式的一般解为其齐次方程的通解加上一个特解,根据高等数学可知其齐次方程有2个特解ρ和ρ-1,因此齐次方程的通解为
设(5)式的特解为u=Cρk,将其代入位移微分方程使其两边相等便可得出其特解为
因此(5)式的一般解为
(6)
将位移方程代入用位移表示的应力应变关系便可以得出应力表达式
(7)
其中A=EA1/(1-ν),B=EB1/(1+ν)。
对于内圆半径为a、外圆半径为b的圆环,以恒定角速度ω旋转,如果其内外边界上均不受力(自由边界),即(σρ)ρ=a=0,(σρ)ρ=b=0。
将以上边界条件代入(7)式,则A,B为
因此,自由圆环应力分量的表达式为
。(8)
同样也可以得出自由圆环位移的表达式为
(9)
根据(8)式对ρ求导并令其为零,得到应力的极大值。当ρ=a时环向拉应力最大,其值为
(10)
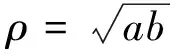
(11)
当ρ=b时径向位移最大,其值为
ν)b2]。
(12)
2 转速对轴承性能的影响
2.1 转速对径向游隙的影响
向心球轴承设计时,其径向游隙(接触角)通常会被视为轴承的一个重要特性参数。它对轴承内部的载荷分布,球的运动状态以及轴承刚度、振动、温升等有重要影响。当轴承高速旋转时由于惯性力的作用套圈将产生膨胀,其结果必然导致轴承沟底直径发生变化,进而导致径向游隙(接触角)发生变化,使轴承的工作性能发生改变。
通常内圈以过盈量I安装于同材料的轴上,内圈内径面所受压力为P1,内圈挡边与沟道表面所受力P2为零,则
将上述边界条件代入(7)式,经整理得内圈沟底的径向位移ui为
由上式可看出内圈的径向位移由过盈和离心膨胀两部分组成。轴承内圈在高转速旋转时由旋转产生的径向位移对径向游隙(接触角)的减小量为
(13)
式中:pi为内圈材料密度;Ei为内圈材料弹性模量;νi为内圈材料泊松比;d为内圈内径;di为内圈沟底直径;ωi为内圈旋转角速度。
2.2 转速对套圈沟道底部应力的影响
轴承的主要失效形式为疲劳失效,而疲劳裂纹的产生与沟道表面的应力状态有密切关系。通常轴承终加工工艺会使沟道表面产生压应力,以抑制疲劳裂纹的产生,从而延长轴承的疲劳寿命。
高速旋转的套圈沟底拉应力同样由过盈和离心效应两部分组成。将安装在轴上的内圈边界条件代入(7)式,经整理得出沟底的周向应力为σi
由上式可看出,内圈的周向应力由过盈和离心膨胀两部分组成,分离出内圈高速旋转引起的沟道底部应力为
(14)
2.3 转速对保持架的影响
高速轴承工作时保持架容易出现失稳和断裂现象,因此设计时必须考虑保持架的强度以及引导间隙。
保持架在轴承内部不受任何约束,其运动和受力状态由钢球和保持架碰撞以及保持架和套圈引导挡边间的润滑剂相互作用决定,因此,分析保持架内部应力分布需要建立多种模型。保持架强度受轴承的工况条件、自身材料及形状等因素影响,还与保持架的动力学有密切关系。在此只分析保持架高速旋转引起的内部最大环向应力,将轴承保持架结构参数代入,其结果为
(15)
式中:pc为保持架材料密度;νc为保持架材料泊松比;dc为保持架内径;Dc为保持架外径;ωc为保持架旋转角速度。
保持架的引导间隙是高速轴承设计的一个主要参数,它会影响轴承的散热与稳定性。轴承高速旋转时,保持架自身的旋转会引起保持架的外径面向外膨胀,使保持架与引导挡边之间引导间隙减小,甚至卡死,因此设计轴承时有必要了解转速对引导间隙的影响。保持架旋转时引导间隙的减小量为δe,其计算式为
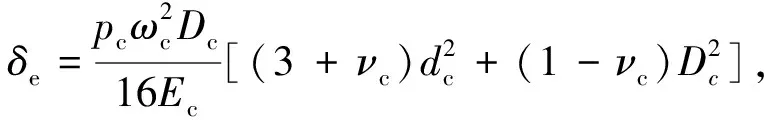
(16)
式中:Ec为保持架材料弹性模量。
3 算例分析
为了更直观地了解轴承转速引起的内圈沟底径向位移变化导致的轴承游隙、沟道上和保持架的应力及引导间隙的变化量,以6005轴承为例计算内圈转速在10 000~30 000 r/min变化时上述各量。轴承内圈材料为G95Cr18不锈轴承钢,保持架材料为塑料。轴承主要结构参数以及材料参数见表1和表2。
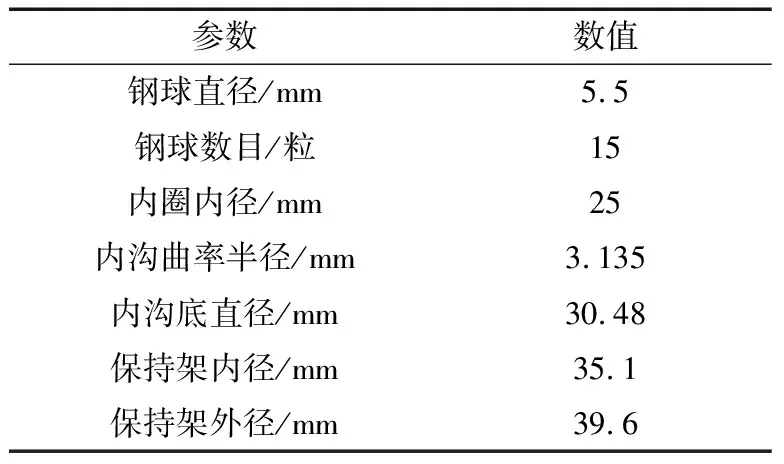
表1 6005轴承结构参数
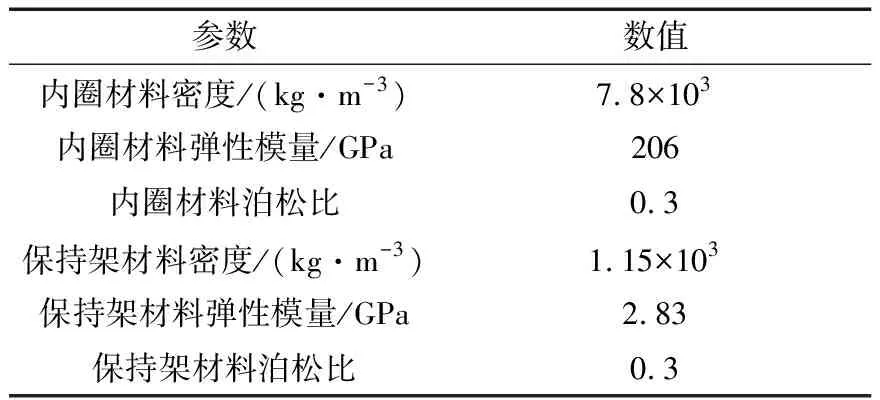
表2 内圈、保持架材料参数
根据轴承运动学可知,保持架转速nm与内圈转速ni之间有如下关系[4]
(17)
式中:Dw为钢球直径;Dpw为球组节圆直径。
根据(13)式和(16)~(17)式可以得出轴承的游隙减小量与内圈转速之间的关系以及保持架引导间隙减小量与内圈转速之间的关系,如图2所示。
图2中ur为轴承径向游隙变化量,εe为保持架与外圈挡边之间的引导间隙变化量。从图中可以看出,轴承径向游隙及引导间隙变化速率随转速增加而增大,当转速为30 000 r/min时,轴承径向游隙减小量最大为2 μm,引导间隙减小量最大为8 μm。

图2 内圈转速引起径向游隙及引导间隙的变化量
同样根据(8)式、(14)~(15)式可以得出轴承高速旋转时内圈沟道表面的拉应力以及保持架内径面上的最大拉应力与内圈转速之间的关系,如图3所示。图3中σi为转速引起内圈沟底位置处的拉应力,σc为转速引起保持架内径面上的拉应力。可以得出轴承在30 000 r/min时由转速引起的内圈沟道底部附加拉应力为16 MPa,导致保持架内径面上的附加拉应力为0.8 MPa。
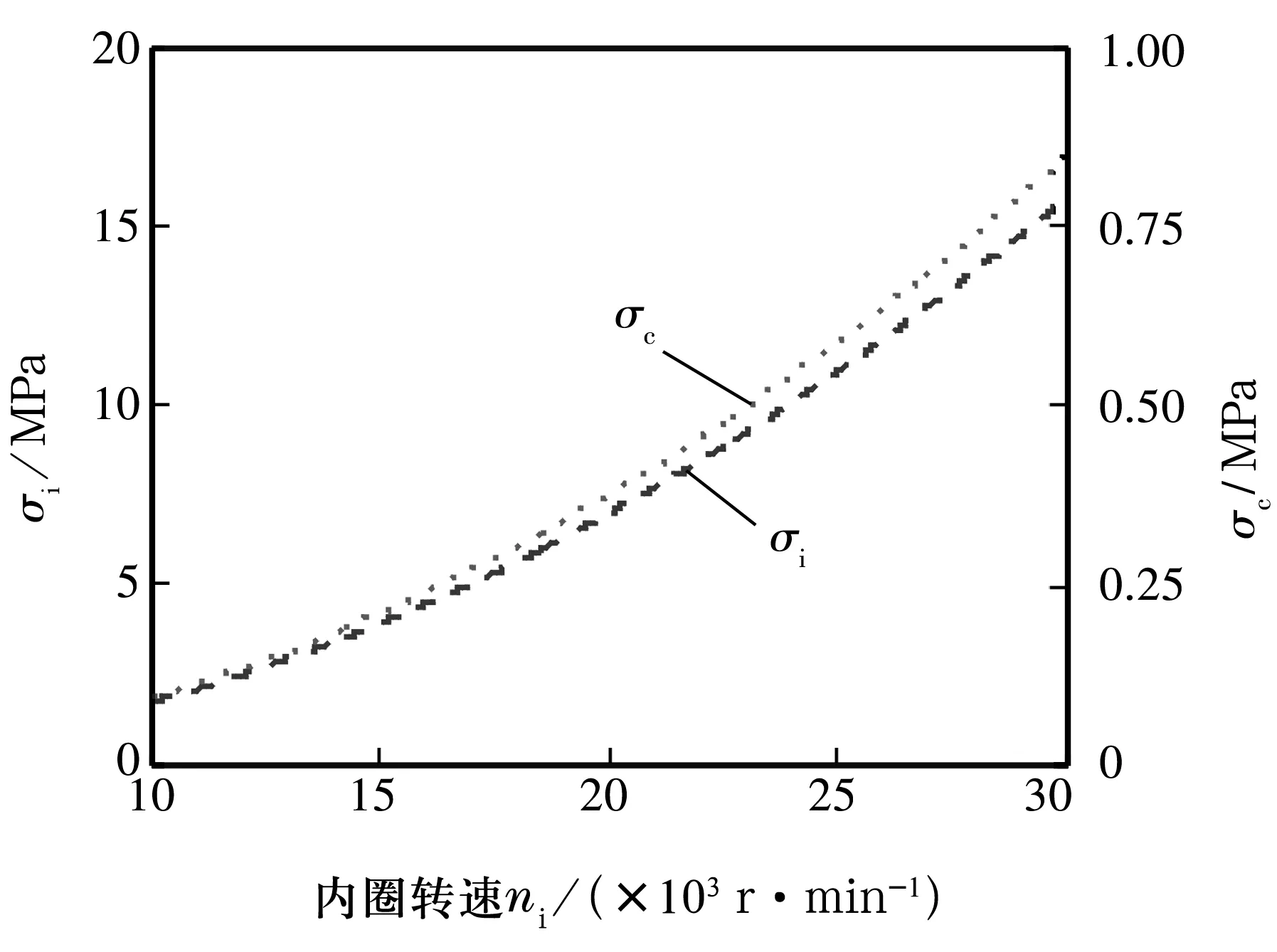
图3 转速与套圈沟底及保持架附加应力的关系
4 结束语
滚动轴承通常认为是高速机械的关键部件。由前面分析可以知道离心应力和位移与转速的平方成正比,因此转速越高,其惯性效应越明显,设计与分析高速轴承时需摒弃轴承零件为刚性体的假设。

