飞行试验航路规划方法研究与实现

刘宇，赵怀慈，花海洋

1.中国科学院沈阳自动化研究所，沈阳 110016

2.中国科学院研究生院，北京 100039

3.中国科学院光电信息处理重点实验室，沈阳 110016

4.辽宁省图像理解与视觉计算重点实验室，沈阳 110016

飞行试验航路规划方法研究与实现

刘宇1，2，3，4，赵怀慈1，3，4，花海洋1，3，4

1.中国科学院沈阳自动化研究所，沈阳 110016

2.中国科学院研究生院，北京 100039

3.中国科学院光电信息处理重点实验室，沈阳 110016

4.辽宁省图像理解与视觉计算重点实验室，沈阳 110016

1 引言

挂飞试验用于测试验证某光电系统在空中对地面目标成像效果和对环境的适应能力。试验时，观测方位角与太阳方位角的相对关系对系统成像效果影响显著，因此需要在特定观测方位角与太阳方位角相对关系下进行试验，试验时航路能否满足预先设定角度关系决定了试验是否能够达到预期效果。此外，试验空域可能存在禁飞区，飞机飞行航路需要规避禁飞区；一次试验需要对多个目标进行观测，且一次试验飞行时间、飞行距离有限，选取合适的目标试验顺序及目标间的航路，使得航程和试验时间较短，对保证试验的可行性有重要意义。

在文献[1]中，航迹使用三维空间中一系列点表示，这种航迹表示方法是较常见的无人飞行器航迹表示方法，但该方法表示的航迹对于本文中有人驾驶情况过于复杂，难以在挂飞试验中应用。本文采用了文献[2]中航路表示方法，即使用顺序相连的线段和弧表示航路。文献[3]所研究的问题与本文中问题相似，并解决了目标点间路径计算及目标点顺序选取问题，但其不需考虑观测点选取问题。由于挂飞试验约束条件的特殊性，特别是与太阳方位角相关的观测点选取问题，在其他文献中并没有涉及，因此需要在本文中提出解决方法。本文针对挂飞试验实际问题，提出了一种飞行试验航路规划方法，该方法可以有效规划出满足试验各种约束条件的航路，为试验顺利进行提供了保证。

2 问题描述

在一次光电系统挂飞试验中，需要分别对多个地面目标进行观测，以测试光电系统成像效果和环境适应能力。试验前对每个目标都确定了观测距离，允许的观测角度范围，观测方位角与太阳方位角夹角范围，试验航路必须满足这三项约束。在试验空域内，可能存在多个禁飞区，飞行航路不能穿越禁飞区。飞机在飞行中，受物自身物理特性制约，不能以小于最小转弯半径进行转弯。一次试验的飞行时间有限，规划航路不能超过飞机一次飞行的最大航程。以上是规划试验路径时主要考虑的约束条件。

本文讨论的航路规划问题在本质上是一个多约束条件下的优化求解问题，可表示为下式：

由于该问题约束较多且较复杂，无法直接求解，本文中采用搜索方法计算试验航路。

整条试验航路由多条子航路组成，每条子航路都由起始于前一目标点（第一条起始于机场除外），终止于当前目标点。子航路组成如图1所示，图中E点为观测点，G点为目标，S点为当前起始点，每条子航路由自由航路和观测段航路两部分组成，其中观测段航路是一条直线段，一端点为目标观测点，另一端点为当前目标。目标观测点位于以目标为中心观测距离为半径的圆上，需要满足禁飞区约束、观测角度范围约束及观测角度与太阳方位角夹角范围约束；自由航路从起始点到目标观测点，需要满足禁飞区约束和最小转弯半径约束。

图1 试验航路示意图

本文所要解决问题是如何在试验的二维空域内规划出一条满足众多约束条件且使航程较短的航路。

本文中将该问题可拆分为以下几个子问题：

（1）求解满足禁飞区约束的最短折线子航路。

（2）选取各目标观测点，使得在满足各项约束下子航路最短。

（3）确定较优的目标观测试验顺序，使得总航程较短。

（4）由折线航路生成满足最小转弯半径约束的航路。

主要解决思路如下：

（1）在起始点、目标观测点确定情况下，构造搜索空间，并在其中进行最短折线航路搜索。

（2）在观测点所在圆上进行离散化处理，选择满足试验各项约束且使得子航路最短的观测点。

（3）使用搜索算法，搜索使得总航程最短的目标试验顺序。

（4）利用几何法[2]在折线航路上计算满足最小转弯半径的试验航路。

3 优化航路计算方法

3.1 可见性图构建及两点间最短折线路径计算原理

穿行于一组互不相交的多边形障碍物S之间，从Pstart通往Pgoal的任何一条最短路径，都是一条多边形路径，其中所有的内部顶点都是S的顶点[4]。构建障碍物S以及起始点目标点的可见性图Gvis(S*)。穿行于障碍物S之间，从Pstart通往Pgoal的任何一条最短路径，必然是由可见性图Gvis(S*)中的若干条弧联接而成的[4]。构建可见性图是在有多边形障碍区域内搜索两点间最短路径的有效方法。这里使用Dijkstra算法在可见性图中进行搜索求解，可得到起始点到目标点的最短路径。Dijkstra算法将连通图转换，构造出以起始点为根节点的树，起始点到某点最短路径可直接从树结构中得到。设障碍物总顶点数为V，则Dijkstra算法将花费O(V2)构建最短路径树Tall，并得到最短路径。图2为Pstart、Pgoal及一组多边形障碍物绘制的可见性图，图中红色多边形为障碍物，Pstart为起点，Pgoal为终点，虚线表示两点间直接可见，黑色实线为Pstart到Pgoal间最短路径。

图2 可见性图及最短路径示意图

3.2 观测点选取策略

观测点选取是本文中要重点讨论的问题之一。观测点的选取直接关系到航路是否满足试验要求，并对总航程有较大的影响。目标的观测距离是试验前确定的，不考虑约束条件，可选以目标为中心观测距离为半径的圆上任意一点为观测点。观测点选取受禁飞区、目标允许观测方向及观测方位角与太阳方位角夹角度范围约束限制。

本文将可能观测点离散化处理，然后搜索求得最佳的观测点。首先将以目标为中心观测距离为半径的圆进行离散化，得到N个可选观测点。本文按照以下原则选取观测点：

（1）观测点不能在禁飞区内部，且观测点至目标的线段不穿越禁飞区（观测点与目标直接可见）。

（2）观测点在目标的可观测方向范围内。

（3）根据得到的航路计算时间，搜索满足此时飞机航路方向与阳光光线间的角度范围的观测点。

在搜索时，从满足以上三条的可选观测点中找到使路径最短的观测点。离散点数N直接关系到搜索算法的精度及时间消耗，越高的离散精度所得到的解精度越高，但耗费计算资源越大。

得到离散的可选观测点后，计算每个可选观测点到多边形障碍顶点及目标点的可见性图，再根据前面的最短路径树Tall可直接得到当前最佳的可选观测点及前一目标到当前目标的最短折线路径。图3为目标点A离散化后的可选观测点与多边形障碍物顶点、目标点构成的可见性图，图中黑色实心矩形为目标，粗实线围成的多边形为障碍物，以目标点A为圆心的圆为可选观测点所在圆，虚线表示两点间直接可见。

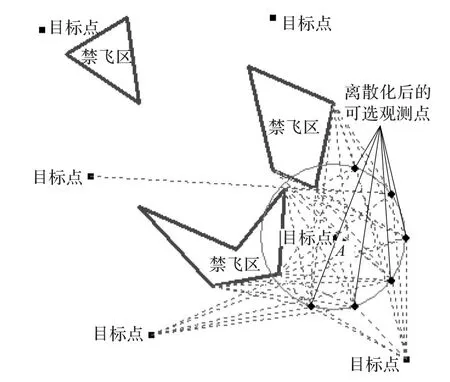
图3 目标点A的可选观测点与顶点、目标点构成的可见性图

3.3 目标顺序搜索过程

如何确定目标顺序使得到的路径较短也是本文中要解决的问题。虽然一次试验中，目标点个数通常不会超过10个，但由于求解某一确定顺序下最短路径的计算量也较大，因此完全遍历方法所需时间也是不能够接受的，并且完全遍历计算量随目标个数增多急剧增加，更不能保证以后处理略多目标情况下算法的可用性。这里选择遗传算法来进行顺序求解。本文所要解决的问题中目标个数较小，属于小规模组合优化问题，较容易得到可接受的解。

遗传算法需要确定如下问题：染色体编码，适应度函数，父代选择，交叉运算，变异运算。本文直接使用目标序号作为染色体编码，如（5-1-7-8-9-4-6-2-3），这样的编码表示目标顺序自然合理；使用当前顺序下得到的折线路径长度作为适应度函数评价标准，认为总长度越小的路径顺序越优；每次从当前种群中选择最优的K个作为下一代的父代；交叉算法采用次序交叉；变异算子采用逆序和互换。计算结果表明，遗传算法能够得到满足试验要求的且较优的目标遍历顺序。图4为采用遗传算法计算得到的折线航路，图中以目标为圆心分布在同一个圆上的点为离散化后的可选观测点，连接目标点观测点及障碍物顶点的虚折线段表示计算得到的折线路径。

图4 计算得到的折线航路

3.4 满足最小转弯半径约束航路计算方法

在生成的折线路径基础上使用几何法生成满足最小转弯半径约束的路径，并且试验中飞机高度、速度不发生变化，不用考虑飞机高度、速度变化问题。在文献[2]中有如下结论：

结论1对于两同方向的航路点，飞机按直线飞行时所飞过的距离最短。

结论2平面内，在某航路点上无人机改变方向的最短路径是按最小转弯圆运动。

由这两条结论可知，满足最小转弯半径约束且最短的航路由转弯半径为最小转弯半径的圆弧及直线段组成。

使用几何法前需要确定飞机在各点的方向，确定方法如下：

（1）若该点为目标观测点或目标点，则该点方向为观测点目标点间线段方向，以保证观测段为朝向目标的直线。

（2）若该点为中间节点且该点不在禁飞区附近，该点方向为前一点至后一点的矢量方向。这样的方向能够保证飞机在中间节点以较优方式进行转弯。

（3）若该点为中间节点且该点靠近禁飞区，则选择与禁飞区边缘平行方向作为飞机飞行方向以确保航路不与禁飞区相交。

确定飞机在各点方向后，使用几何法可得到满足最小转弯半径约束的飞行航路。图5为最终计算所得的由弧和线段组成的，满足所有试验约束条件的航路。

图5 由圆弧和线段构成的最终飞行航路

4 航路规划应用实例

以一次挂飞试验航路规划过程为例，详细试验要求如下：

挂飞试验时间为2011年11月24日9：00，观测目标为四个目标，每个目标观测两次，每次观测的参数不同，表1是试验目标的各项参数。试验载机飞行速度为150 km/h。

表1 目标实验参数

规划航路结果如图6所示。图6中实心矩形为目标，线路上空心圆形为观测点，从图中可以看出，计算得到的试验航路满足禁飞区约束，且保证了路线的优化，满足一次试验的时间、航程要求；从表2中可知每个所选观测点都满足设定的观测方向范围约束和与太阳方位角夹角范围约束，因此该航路完全符合试验的各项要求。算例证明该航路规划算法可以为挂飞试验提供满足各项约束的航路。

5 结论

本文针对光学系统挂飞试验路径规划问题提出了一种有效的航路规划算法。通过构造可见性图形成搜索空间，使用Dijkstra算法求得两点间最优路径段，离散化可选观测点并搜索最适合的观测点，使用遗传算法搜索较优的目标顺序，最后使用几何法得到满足最小转弯半径约束的飞行路径。计算结果表明，本文算法所得到的试验航路能够满足试验的各项约束，为光电系统挂飞试验提供了有力的支持。

图6 根据试验条件规划出的一条可行航路

表2 计算结果

[1]丁明跃.无人飞行器航迹规划[M].北京：电子工业出版社，2009.

[2]王庆江，高晓光，符晓卫.无威胁情况下任意两点间的无人机路径规划[J].系统工程与电子技术，2009，31（9）：2157-2162.

[3]Luo Quan，Liu Zhong，Qiao Shidong.A hybrid route planning algorithm of single aerial vehicle attacking multiple targets[C]//ProceedingsoftheNinthInternationalConference on Machine Learning and Cybernetics，2010：1532-1537.

[4]德贝尔赫.计算几何——算法与应用[M].邓俊辉，译.2版.北京：清华大学出版社，2005.

[5]维斯.数据结构与算法分析——C语言描述[M].冯舜玺，译.2 版.北京：机械工业出版社，2004.

[6]李敏强.遗传算法的基本理论与应用[M].北京：科学出版社，2002.

LIU Yu1，2，3，4,ZHAO Huaici1，3，4,HUA Haiyang1，3，4

1.Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,China
2.Graduate School,Chinese Academy of Sciences,Beijing 100039,China
3.Key Lab of Opto-Electronic Information Processing,Chinese Academy of Sciences,Shenyang 110016,China
4.Key Lab of Image Understanding and Computer Vision,Liaoning Province,Shenyang 110016,China

Τhe flying test of an opto-electronic module has high demand to the aircraft route,and a route that satisfies the constraints of the test is the precondition to fulfill the objective of the test.According to this question,a search space construction method based on visibility graph is used here；the shortest polylines path between two targets is got by the Dijkstra algorithm；the GA algorithm is used to get an optimized order of targets；then the final route is got from the polylines path and minimum turning radius is satisfied.Τhe result shows that this route computing method can be well used to get an aircraft route which satisfies the constraints of the opto-electronic module test.

route planning;visibility graph;Dijkstra algorithm;combinational optimization;Genetic Algorithm（GA）

光电系统挂飞试验对飞行航路有较高要求，一条能够满足试验各项约束的航路是试验按计划完成的前提。针对该问题，提出了一种基于可见性图的航路搜索空间构造方法；使用Dijkstra算法计算顺序两目标点间的折线路径；使用遗传算法计算代价最小的目标观测顺序；在得到的折线路径上计算得到满足最小转弯半径约束的航路。计算结果表明，这种航路算法能够有效规划出满足挂飞试验多约束条件的航路。

航路规划；可见性图；Dijkstra算法；组合优化；遗传算法

A

ΤP273.5

10.3778/j.issn.1002-8331.1201-0301

LIU Yu,ZHAO Huaici,HUA Haiyang.Research and implementation of route planning method for flying test.Computer Engineering and Applications,2013,49（21）：262-265.

刘宇（1987—），男，硕士在读，主要研究领域为任务规划及仿真；赵怀慈（1974—），男，博士，研究员；花海洋（1978—），男，助理研究员。E-mail：liuyu@sia.cn

2012-01-16

2012-02-27

1002-8331（2013）21-0262-04

CNKI出版日期：2012-06-01http://www.cnki.net/kcms/detail/11.2127.ΤP.20120601.1457.013.html