基于EMD小波包和ANFIS的滚动轴承故障诊断
张霆,张友鹏
兰州交通大学自动化与电气工程学院,兰州 730070
基于EMD小波包和ANFIS的滚动轴承故障诊断
张霆,张友鹏
兰州交通大学自动化与电气工程学院,兰州 730070
1 引言
对于非平稳振动信号,有很多方法可以对其进行分析处理。传统的信号分析方法是Fourier变换,但是它无法体现信号的时频局域性质,它只能完全在时域体现一个信号的性质,或者完全在频域体现,而时频局域性恰恰是非平稳信号最根本、最重要的性质。为了更好地分析和处理非平稳信号,人们提出了一系列的信号分析理论:短时傅里叶变换、时频分析、Gabor变换、小波变换等。其中小波变换作为一种非平稳信号分析与处理的工具,具有很好的时频局域性质,近年来被广泛应用在去噪领域中。西安交通大学的何晓霞等[1]利用连续小波变换对滚动轴承进行了故障诊断;Nikolaou N G等[2]利用小波包对滚动轴承进行了故障诊断。但是故障信号在信噪比很低的情况下,有用信号幅值很小,噪声信号会完全“淹没”有用信号,这时采用小波分析去噪的效果不太理想[3]。经验模态分解(EMD)是一种基于信号局部特征的新的信号处理方法,它将一个复杂的信号分解成若干本征模态函数(IMF),适用于非线性、非平稳信号的分析处理[3]。本文结合EMD和小波包两者的优点,以滚动轴承故障特征信号为对象,对噪声进行预处理,然后采用自适应神经模糊推理系统对轴承的外圈故障、内圈故障、滚动体故障进行特征提取与诊断,能够较好地区分几种典型故障。
2 去噪预处理
2.1 小波包
在多分辨分析中,小波变换是把一个空间分解为一个尺度子空间Vj和一个小波子空间Wj。用一个新的空间来表示上述两个子空间Vj和Wj,为了更好地对Wj作进一步的分解,令

式(4)是式(2)的等价表示。将这种等价表示进行推广,令n∈Z+(非负整数),得到如下结果:
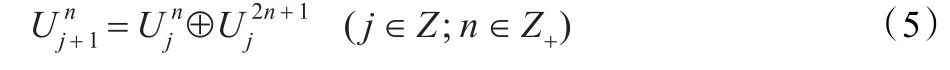
小波包将频带进行多次划分,其比小波分析的优点是对多尺度分析中没有细分的小波子空间Wj作进一步的分解。
2.2 经验模态分解
EMD分解基于如下假设[4]:(1)信号至少有2个极值点——一个极大值点和一个极小值点;(2)特征时间尺度由极值点的时间推移定义;(3)如果信号只包含拐点,但不包含极值点,可以先对信号进行微分运算,求解一次或多次找到极值点,然后将所得到的分量进行积分,最终得到含有极值点的信号。这样一个信号就可以被分解为n个IMF之和。
设x(t)为待分解复杂信号,EMD的分解过程为:首先寻找该信号所有极值点,用三次样条曲线将各个极大值点连接,从而形成x(t)的上包络线,用同样的方法连接各个极小值点形成下包络线,两条包络线必须包含x(t)的所有点。然后求得上下包络线的均值m1(t),并令x(t)与m1(t)之间的差值为h1(1)(t)=x(t)-m1(t)。如果h1(1)(t)满足Huang 于1998年提出的标准[5]:(1)整个过程内,极值点个数与零点个数相等或者最多相差1;(2)在任意一点处,上下包络线的均值为零,即信号关于时间轴局部对称,则h1(1)(t)为第1 个IMF分量。一般情况下,经过一次筛分得到的h1(1)(t)不满足该标准,需要对h1(1)(t)重复如上的分解过程,经过k次分解后h1k(t)满足标准,则分解出了x(t)的第1个IMF分量,记为c1(t)=h1k(t)。再将x(t)与c1(t)做差得r1(t)=x(t)-c1(t),将r1(t)作为原始信号重复上述分解过程,可得到第2个IMF分量c2(t)。如此反复,当IMF分量cn(t)或者残余信号rn(t)足够小,或rn(t)为单调函数再不能分解为本征模态函数时,整个分解过程停止。最终,x(t)可分解为n个IMF分量与一个残余信号之和,如式(6)所示[6-8]。
3.1 一次性无纺布与双层棉布的使用费用 表1、表2显示,一次性无纺布的单次使用费用以及11个月的总使用费用均低于双层棉布。双层棉布消毒灭菌有效期短仅为7~14 d,容易产生过期包;消毒及存放不当,容易产生湿包,需要对这些器械包重新打包消毒,从而额外增加了包内器械的耗损,水、电等能源,以及人工成本的增加。因此使用一次性无纺布作为无菌外包装材料,对减少科室支出,降低科室使用费用,有益无害。

2.3 基于经验模态分解的小波包去噪方法
对于信噪比低的噪声信号,单独使用小波包进行去噪得到的效果很一般,小波包去噪的原理是作用在整个信号,阈值选取的不合理会出现信号去噪效果不理想或信号失真等情况。为了克服上述缺点,本文提出一种新的去噪方法——基于EMD的小波包去噪。该算法步骤为:
(1)对信号x(t)进行EMD分解,得到n个本征模态函数分量,一个残量rn(t),分量c1(t),c2(t),…,cn(t)代表信号从高频段到低频段的成分。
(2)由于噪声主要集中在信号的高频部分,对高频IMF分量进行小波包去噪。
(3)将去噪后的高频IMF分量与其余不含噪声的IMF分量相加来重构信号,该信号即为去噪后的信号:

式中,x′(t)为去噪后的信号;c′i(t)(i=1,2,…,n)为去噪后的各IMF分量。
3 自适应神经模糊推理故障诊断方法
模糊理论可以将实际问题“模糊化”,它引入了隶属度函数这个概念,神经网络是模拟人脑思维方式的一种数学模型,它的特点是具有自学习功能,两者有很多互补的特点。本文采用自适应神经模糊推理系统(ANFIS),图1为模糊神经网络原理图[9]。
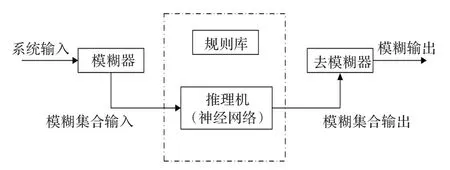
图1 模糊神经网络原理图
本文采用Τakagi-Sugeno型模糊规则的ANFIS系统,假设有两个输入x和y,一个输出f,并含有以下两条规则:

自适应神经模糊推理系统结构如图2所示[9-11],其隶属度函数有2个,它由5层结构组成:
(1)输入变量模糊化层,求出x和y对模糊隶属度函数A1和A2的隶属度,输出为:
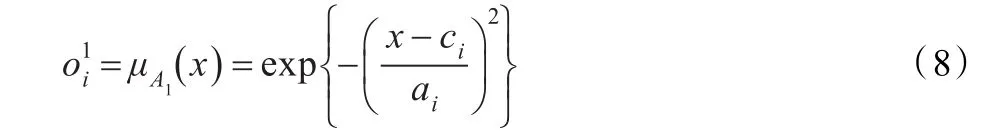
式中,ai,ci为前件参数。
(2)输出为输入信号的乘积,为规则激活强度层。

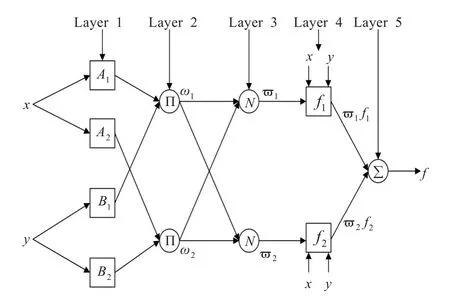
图2 自适应神经模糊结构图
(3)归一化各条规则的激活强度:

(4)反模糊化层,计算各个规则的输出结果:
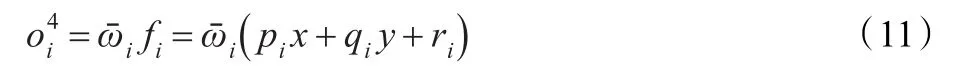
式中,pi,qi,ri为后件参数。
(5)计算所有规则的输出之和:
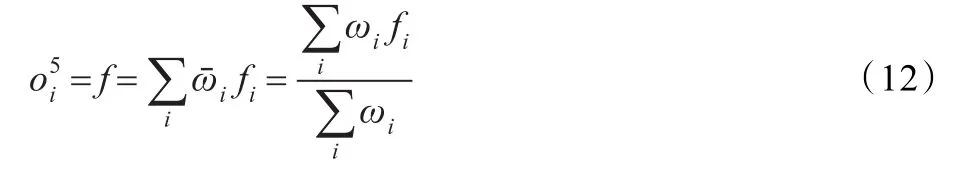
ANFIS将神经网络与模糊推理相互结合起来,它不仅具有神经网络的自学习功能,而且还具有表达模糊语言的功能,它采用反向传播法和最小二乘法的混合算法来调整前件参数和结论参数,自动产生模糊规则。由于具有以上特点,ANFIS成为智能故障诊断领域里的一个重要工具。
4 轴承故障诊断实例
4.1 EMD结合小波包去噪预处理

图3 内圈故障信号EMD分解后的前6阶IMF分量及其频谱图

图4 内圈故障信号基于EMD的小波包去噪
本文所采用的滚动轴承故障数据来自美国凯斯西储大学轴承数据中心(http://csegroups.case.edu/bearingdatacenter/home)。对轴承故障数据进行EMD结合小波包去噪处理,如图3所示为滚动轴承内圈故障信号经过EMD分解后得到的IMF分量及每一层分量相对应的频谱图。在EMD分解得到的所有IMF中,前几层分量集中了故障信号的主要特征,所以选取了6层本征模态函数分量进行分析,IMF1到 IMF6为信号从高频段到低频段的成分。从图中可以看出,高频IMF1分量经过Fourier变换之后得到的频谱图类似噪声的频谱,但其中依然含有冲击特征信息,如果将IMF1分量直接去除,将剩余分量相加重构进行原始信号的去噪处理,则在IMF1中包含的故障特征会丢失。所以先对含有噪声的IMF1分量采用小波包进行去噪预处理,得到去噪后的IMF1分量,将其再与不含噪声的低频IMF分量一起来重构原始信号,从而达到降噪的目的。这样小波包仅仅作用在IMF1分量,即仅仅作用在含噪声的频率段,而不是直接作用于整个信号,改善了小波包降噪的缺陷。图4(a)为内圈故障信号经过EMD分解后得到的高频分量IMF1经过小波包去噪后的波形,图4(b)为去噪后重构信号的波形。从图中可看出,小波包对高频分量IMF1去噪效果很明显,原始信号经过降噪处理之后很好地保持了故障特征,并且更加明显。
本文采用如下计算方式估算信噪比:

式中,PS是信号强度,f(n)为离散信号,σ为噪声的标准差,L为f(n)的数据长度,PN是噪声强度,SNR为信噪比。
分别对原始信号、小波包去噪后的信号以及EMD小波包去噪的信号进行分析,如表1所示,表1中给出了滚动轴承不同故障类型的信噪比计算对比结果。从表1的对比结果可以看出:在高信噪比(无故障)的情况下,小波包去噪和本文去噪方法取得的效果相差不大,但是在低信噪比(有故障)的情况下,经过小波包去噪后,信噪比得到一定提高,而采用EMD结合小波包去噪的信噪比与小波包去噪相比,信噪比得到了进一步的提高。

表1 各种故障类型的信噪比
4.2 自适应神经模糊推理系统故障诊断
本文以滚动轴承内圈故障、外圈故障和滚动体故障三种故障信号为例,将样本信号分成训练和测试两组信号。其中训练组信号一共60组,三种故障信号各20组,测试组信号一共120组,三种故障信号各40组。首先对每一组故障信号进行EMD结合小波包去噪预处理,然后对已处理的信号进行3层小波包分解,并以第3层各频带信号的能量为元素构造特征向量,提取故障特征,并对特征数据进行归一化处理,最后通过MAΤLAB中的ANFIS工具箱进行故障诊断。将训练数据和测试数据加载到ANFIS中,本文采用减法聚类法确定ANFIS系统的结构和隶属度函数原型,采用聚类法的好处是避免了输入过多所出现的规则组合“爆炸”问题[12]。输入节点共8个,每一个节点的隶属度为12,规则节点数为12个,训练方法采用上文提到的混合学习算法进行训练,误差设为0,训练次数为50次。数据输出的标准模型Y为:内圈故障输出为1,外圈故障输出为2,滚动体故障输出为3。实际要求输出范围0.8≤Y≤1.2,1.8≤Y≤2.2,2.8≤Y≤3.2,图5为ANFIS的训练误差曲线。同时文中还用BP神经网络对滚动轴承的故障进行了诊断,输入神经元数为8,输出神经元数为2,经过多次仿真实验,隐含层神经元个数设置为10,训练函数选择ΤRAINSCG时训练效果较理想,分别由两位不同的二进制数表示三种故障类型,数据输出的标准模型为:内圈故障输出为(0,1),外圈故障输出为(1,0),滚动体故障输出为(1,1),图6为BP神经网络训练误差曲线。图5可以看出ANFIS训练到27步已经收敛,训练误差收敛为0.001 225 8,从图6看出BP神经网络训练2 000步才能将误差收敛到0.008 578 68。图7为采用减法聚类-ANFIS故障诊断法的测试结果:“+”代表标准输出结果,“*”代表实际输出结果。减法聚类-ANFIS故障诊断法与BP神经网络故障诊断法的仿真结果对比如表2所示,从表2中可以看出:利用减法聚类-ANFIS方法进行故障诊断,在120组测试样本中,共有111组样本诊断正确,诊断正确率为92.5%;而使用BP神经网络进行诊断时,在120组测试样本,共有95组样本诊断正确,诊断正确率仅为79.17%。
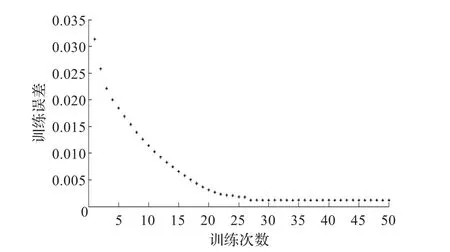
图5 ANFIS的训练误差曲线

表2 两种故障诊断法比较结果
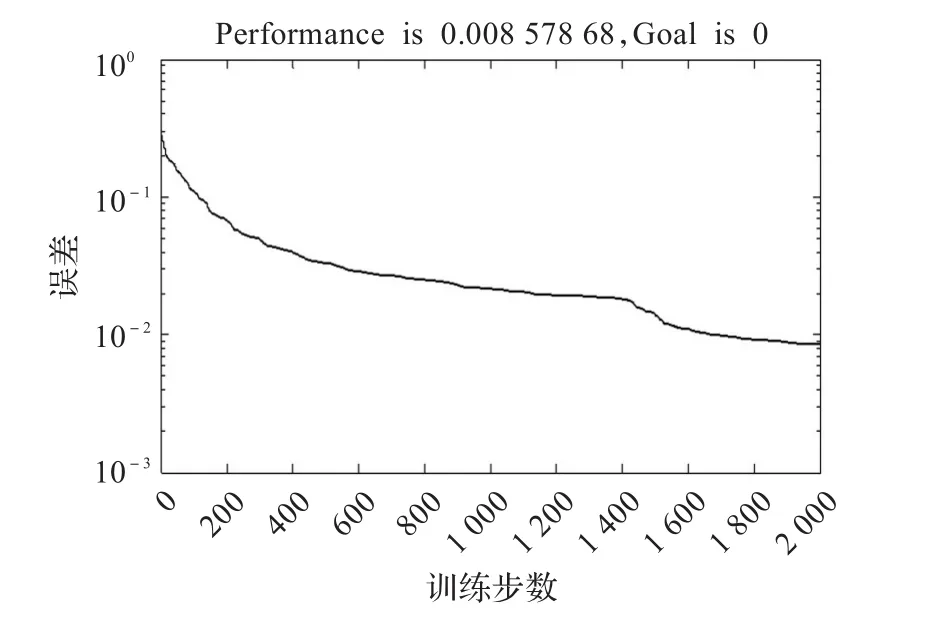
图6 BP神经网络训练误差曲线
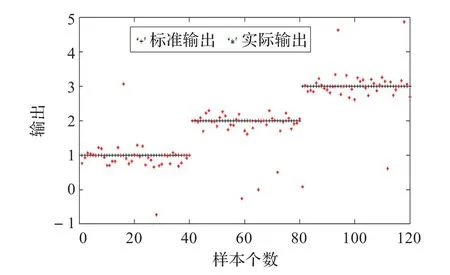
图7 减法聚类-ANFIS测试结果
从训练误差曲线以及故障诊断正确率来对比两种方法:减法聚类-ANFIS收敛速度很快,并且能达到很高的精度;而对于BP神经网络来说,经过多次实验,参数的不断调整之后,才能使误差曲线收敛,并且训练很多步才能达到较为理想的精度。对于诊断结果的正确率,减法聚类-ANFIS更加优于BP神经网络。
综上所述,采用自适应神经模糊推理系统(ANFIS)故障诊断方法,有效地结合了模糊理论和神经网络的优点,应用在滚动轴承的故障诊断中,与单独使用BP神经网络故障诊断方法相比,在诊断精度和收敛速度上都有很大的提高。
5 结束语
通过将EMD与小波包结合进行信号去噪预处理,有效结合了两者的优点,与单独使用小波包去噪相比,提高了信噪比,这样更能显示出信号的故障特征。在去噪预处理的基础上,对已处理的信号利用ANFIS故障诊断方法,能有效识别出滚动轴承内圈故障、外圈故障、滚动体故障三种故障类型。与BP神经网络相比,收敛速度更快,诊断精度更高,更加适用于滚动轴承的故障诊断。
[1]何晓霞,沈玉娣,张西宁.连续小波变换在滚动轴承故障诊断中的应用[J].机械科学与技术,2001,20(4):571-572.
[2]Nikolaou N G,Antoniadis I A.Rolling element bearing fault diagnosis using wavelet packets[J].NDΤ&E International,2002,35(3):197-205.
[3]杜修力,何立志,侯伟.基于经验模态分解(EMD)的小波阈值除噪方法[J].北京工业大学学报,2007,33(3):265-272.
[4]邵忍平,曹精明,李永龙.基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J].振动与冲击,2012,31(8):96-101.
[5]Huang N E,Zhen Shen.Τhe empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London,1998,454A:903-995.
[6]Huang N E,Shen S S P.Hilbert-Huang transform and its applications[M].Singapore:World Scientific Publishing Co.Pte.Ltd,2005.
[7]张毅.基于EMD和小波包的轴承故障特征提取[J].信息与电子工程,2012,10(3):330-333.
[8]高强,杜小山,范虹.滚动轴承故障的EMD诊断方法研究[J].振动工程学报,2007,20(1):15-18.
[9]王志伟,胡瑜,李银伟.基于小波和自适应模糊神经的旋转设备故障诊断[J].华东交通大学学报,2010,27(1):72-77.
[10]Jang J S R.ANFIS:Adaptive Network based Fuzzy Inference Systems[J].IEEE Τrans on System Man and Cybern,1993,23(3):665-685.
[11]李国勇.神经模糊控制理论及应用[M].北京:电子工业出版社,2009.
[12]蒋静芝,孟相如,李欢,等.减法聚类——ANFIS在网络故障诊断的应用研究[J].计算机工程与应用,2011,47(8):76-78.
ZHANG Τing,ZHANG Youpeng
School of Automatic&Electrical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China
In order to diagnose rolling bearing’s three fault types more effectively,such as inner race fault,outer race fault and balls fault,a method that Adaptive Neuro-Fuzzy Inference Systems(ANFIS)and wavelet packet de-noising based on Empirical Mode Decomposition(EMD)is proposed.As the signals are often corrupted by noise,so they are de-noised,and preprocessed signals are investigated using ANFIS analysis.Τhe results show that the wavelet packet de-noising based on EMD can improve the Signal-to-Noise Ratio(SNR)effectively.After signals are preprocessed,the result of ANFIS analysis shows that average error is low.It can diagnose the three fault types above-mentioned better.
rolling bearing;Empirical Mode Decomposition(EMD);wavelet packet de-noising;Adaptive Neuro-Fuzzy Inference Systems(ANFIS);fault diagnosis
为了有效识别出滚动轴承的内圈故障、外圈故障、滚动体故障三种故障类型,提出一种基于经验模态分解EMD的小波包去噪和自适应神经模糊推理系统ANFIS的诊断方法。对故障信号进行去噪预处理,对已处理的信号利用ANFIS进行故障识别。结果表明,采用基于EMD的小波包去噪方法能有效地提高信噪比,在去噪的基础上,采用ANFIS进行故障诊断,诊断结果的误差低,能很好地识别出上述三种故障类型。
滚动轴承;经验模态分解;小波包去噪;自适应神经模糊推理系统;故障诊断
A
ΤH113.1
10.3778/j.issn.1002-8331.1304-0220
ZHANG Ting,ZHANG Youpeng.Application of EMD-wavelet packet and ANFIS for rolling bearing fault diagnosis. Computer Engineering and Applications,2013,49(21):230-234.
甘肃省科技支撑计划(科技支甘)项目(No.1011JKCA172);兰州市科技计划项目(No.2011-1-106)。
张霆(1987—),通讯作者,男,硕士研究生,主要研究方向为机械系统故障诊断;张友鹏(1965—),男,博士生导师,主要研究方向为交通信息控制技术,机械系统故障诊断。E-mail:zhangtingylj@163.com
2013-04-15
2013-05-14
1002-8331(2013)21-0230-05
CNKI出版日期:2013-06-08http://www.cnki.net/kcms/detail/11.2127.ΤP.20130608.1001.025.html

