基于分离度变步长的自然梯度算法的语音分离

刘俊良，于凤芹

江南大学物联网工程学院，江苏无锡 214122

基于分离度变步长的自然梯度算法的语音分离

刘俊良，于凤芹

江南大学物联网工程学院，江苏无锡 214122

1 引言

盲源分离是指从若干个观测到的多个信号的混合信号中恢复出无法直接观测到的原始信号的方法[1]。语音信号分离问题是盲源分离的一个重要领域，国内外许多学者都对其作了很多研究[2-4]，要解决这一问题最常用的方法就是基于独立成分分析（Independent Component Analysis，ICA）的方法[1]，以源信号间的统计独立性为判据设定目标函数，然后通过各种算法使其最小化，最终求出分离矩阵，得到源信号。自然梯度算法是一种最小均方误差算法，通过寻找目标函数最小化的最快下降方向实现对混合信号的快速分离，对数据进行在线迭代处理，具有很好的实时性[5]。在这种算法中，步长与稳态误差成正比，而步长又与收敛时间成反比，使得收敛速率和稳态误差不能同时满足。要解决这一问题，比较好的做法就是采用自适应的步长。文献[6]根据梯度实时调整步长，并用一个符号函数减少算法的计算量，收敛速率有所提高，稳态误差基本不变。文献[7]通过建立步长因子与四阶统计量峭度之间的非线性关系，对固定步长算法作了改进，提高了算法的收敛速度，稳态误差略微减少。本文采用一种变步长的算法，应用于两个混合语音信号的分离之中，根据实际的分离度动态调整步长，设置两个参数作为分离度的系数分别控制收敛速率和稳态误差，并结合串音误差确定这两个参数的最佳取值。仿真实验结果表明新的算法相较固定步长算法，收敛速率提高了将近1倍，同时稳态误差缩减小3倍，获得了较好的语音分离效果。

2 自然梯度算法理论

2.1 盲源分离模型

假设未知源信号S(t)=(s1(t)s2(t)…sn(t))Τ是零均值且相互独立的量，X(t)=(x1(t)x2(t)…xn(t))Τ是观测到的量，它是由S(t)经线性瞬时混合得到，混合公式如下：

其中A∈Rn×m是一个未知的满秩混合矩阵。

盲分离就是在没有任何先验知识和混合矩阵A未知的情况下仅由观测信号X(t)恢复源信号S(t)的过程。

解混的线性变换模型如下式：

其中Y(t)=(y1(t)y2(t)…yn(t))Τ是对源信号S(t)的估计，W∈Rn×m是要求解的分离矩阵。盲分离算法就是要寻找分离矩阵W。

2.2 自然梯度算法原理

在盲源分离中，输出信号Y(t)的相互独立性反映了分离的质量，常以Kullback-Leibler散度作为独立性的测度，并使其最小化。记随机变量Y=WX的概率密度函数为py(Y,W)，建立一个所有分量均是统计独立的q(Y)作为参考。当且仅当py(Y，W)与q(Y)具有相同的分布时，KL散度为零，而且不随变量yi的非线性变换而变。独立性的自然测度以公式表示为：

3 基于分离度变步长的语音盲分离算法

在传统自然梯度算法中，步长因子μ(k)通常采用固定值，这样有可能导致收敛速度慢，算法的跟踪性差，最终影响整个分离过程的结果。这是由于采用固定的步长，自然梯度算法存在收敛速率和稳态误差之间的矛盾。步长取得较大，则收敛速率较快，稳定误差较大；步长取得较小，则稳态误差较小，但是收敛速率较慢。因此要解决这个问题，必须采用自适应的步长。

本文采用一种自适应变步长的分离算法，它的基本原理是建立自然梯度法与步长因子μ(k)之间的非线性联系，使步长因子随分离效果而变化，不用太多考虑初始步长的选择问题，可以达到比较好的分离效果。

首先定义一个变量D(k)表示当前的分离效果，其值如下式：

为了增强分离的效果，可使步长因子μ(k)根据实际分离效果，即D(k)的当前值在较小范围内自动调整，参数α(k)按照以下方式进行取值：

式中0〈γ，β〈1，D(0)=0。即参数γ控制收敛速率，β控制稳态误差。

最终新的自适应步长自然梯度算法公式为：

本文的算法具体实现步骤为：

第一步，对输入的混叠语音信号进行零均值化处理。

第二步，将第一步得到的语音信号进行白化处理，获得白化的数据矩阵Z。

第三步，设置初始分离矩阵W(0)，选择初始步长μ(0)。

第四步，通过计算得到分离的语音信号Y=WZ。

第五步，计算f(Y(k))YΤ(k)。

第六步，计算D(k)，并求出步长因子μ(k+1)。

第七步，更新分离矩阵W(k+1)。

第八步，验证是否收敛，如果没有则返回步骤四。

4 仿真实验结果与分析

本实验针对的是两个语音信号的线性瞬时混合，为一段男声和一段女声，采样频率为16 kHZ，选取25 000个采样点，设置初始分离矩阵W(0)=0.1*I，采用激活函数f(y)= tanh(y)，选取初始步长μ(0)=0.05，迭代次数设定为100次，初次迭代梯度算法控制因子D(0)=0，混合矩阵A是由matlab软件随机生成的2行2列的矩阵，在matlab平台进行仿真实验。

为了定性地评价算法的性能采用串音误差和相似系数矩阵来作为评价标准。串音误差的数学表达式为：

式中Ci，j代表矩阵C中第i行j列的元素，矩阵C=WA为混合分离矩阵，E就是串音误差，它的值越小，表示分离的效果越好。相似系数矩阵是用来表示所得到的分离信号与源信号之间相似程度的一个量，当相似系数矩阵每行每列都有且仅有一个元素为接近1，其他元素都接近0时，表示分离的效果较好。

4.1 β和γ的取值

为了得到最佳的分离效果，需要通过仿真实验确定两个控制参数β和γ的值。本文采用逐个确定的方法，先固定一个参数，然后优化另一个参数，本文先取β的值，β的大小影响稳态误差，经过仿真实验，综合决定：

（1）固定β的值为0.1，调整γ的值，如图1所示，可以看出随着γ值的减小，串音误差达到稳定时所需要的迭代次数明显增加，所以本文选择γ的取值为0.1。

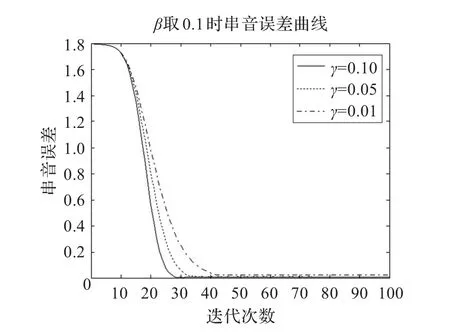
图1 固定β串音误差曲线图

（2）固定γ的值为0.1，调整β的值，如图2所示，可以看到随着β的减小，串音误差达到稳定时所需的迭代次数略微增加，但是稳态误差明显减小，综合考虑，本文选择β的取值为0.1。

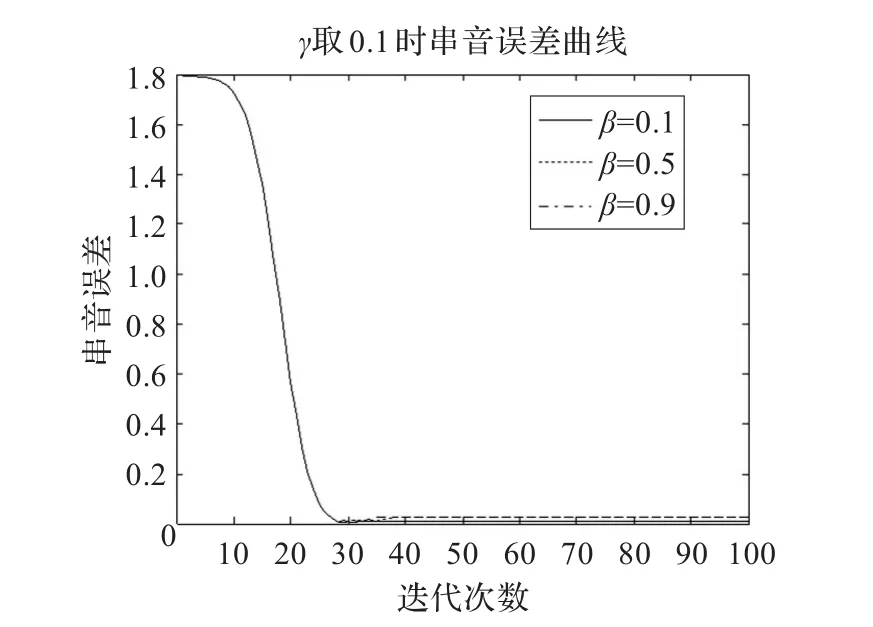
图2 固定γ串音误差曲线图

4.2 与固定步长自然梯度算法的对比

通过表1看到，两个算法的相似系数矩阵表明自适应步长算法分析效果更好，自适应步长算法的稳态误差为固定步长算法的1/3，稳态误差大大减小。

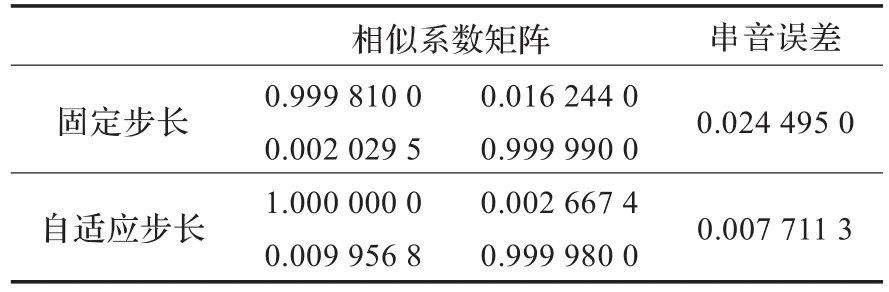
表1 算法性能指标对比

图3 原始语音信号

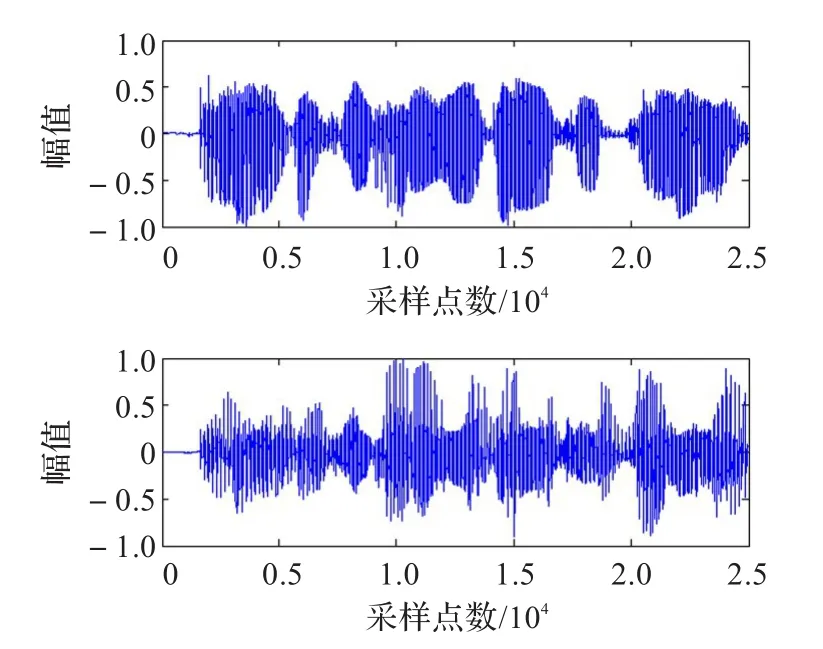
图4 混合语音信号

图5 固定步长算法分离的语音信号

图6 自适应步长算法分离的语音信号

从图3到图6可以直观看出，相较固定步长自然梯度算法，自适应步长算法分离出的语音信号与源语音信号更为相近，表明分离的效果更好。而从图7可以看到，相较固定步长算法迭代50次才收敛，自适应步长算法在迭代30次时就已收敛，收敛速率提高了将近一倍，同时稳态误差也明显低于固定步长算法。

图7 固定步长算法和自适应步长算法的串音误差曲线图

5 结束语

本文采用一种适用于语音信号分离的自适应步长自然梯度算法，通过分离度自动调整步长，不断优化分离矩阵，通过实验验证了该算法分离语音信号的有效性。仿真实验结果表明新算法能够在大幅度降低稳态误差的情况下同时提高收敛速率，较好地解决了收敛速率和稳态误差相矛盾的问题，获得了较好的语音分离效果。

[1]史习智.盲信号处理——理论与实践[M].上海：上海交通大学出版社，2008：45-54.

[2]梁淑芬，江太辉.一种自适应算法的语音信号盲分离[J].信号处理，2010，26（7）：1094-1098.

[3]Bulek S，Erdol N.Blind speech separation using fractional order moments[C]//Statistical Signal Processing，2009：509-512.

[4]Benabderrahmane Y，O’Shaughnessy D，Selouani S A.Blind speech separation using OPCA method[C]//Industrial Electronics&Applications，2009：743-747.

[5]Amari S.Natural gradient works efficiently in learning[J]. Neural Computation，1998，10（2）：251-276.

[6]Yuan L X，Wang W W，Chambers J A.Variable step-size sign natural gradient algorithm for sequential blind source separation[J].IEEE Signal Processing Letters，2005，12（8）：589-592.

[7]王灵伟，舒勤，陈龙飞.峭度自然梯度盲分离改进算法[J].计算机工程与应用，2011，47（11）：132-134.

LIU Junliang,YU Fengqin

School of Internet of Τhings Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China

Τo solve the contradiction that fixed step size natural gradient algorithm brings between convergence rate and steadystate error,a natural gradient algorithm based on adaptive step size is adopted that step size changes automatically depending on separation degree,and two parameters are used as the coefficient of separation degree to control separate stability and convergence. Simulation results demonstrate that the algorithm has good separation property compared with fixed step size algorithm.Convergence rate doubles,and steady-state error narrows three times.

blind source separation;speech separation;adaptive step size;separation degree;convergence rate;steaty-state error

为解决固定步长自然梯度算法带来的收敛速率与稳态误差之间矛盾的问题，采用一种自适应步长的自然梯度算法，根据实际分离度自动调整步长，通过设置两个参数作为分离度系数控制收敛速率和稳态误差。仿真实验结果表明相较固定步长算法，该算法具有较好的分离性能，收敛速率提高了1倍，同时稳态误差缩小了3倍。

盲源分离；语音分离；自适应步长；分离度；收敛速率；稳态误差

A

ΤN912

10.3778/j.issn.1002-8331.1203-0052

LIU Junliang,YU Fengqin.Speech separation based on variable step size natural gradient algorithm depending on separation degree.Computer Engineering and Applications,2013,49（21）：216-219.

国家自然科学基金（No.61075008）。

刘俊良（1989—），男，硕士，主要研究领域为语音信号处理；于凤芹（1962—），女，博士，教授，主要研究领域为语音信号处理。E-mail：yufengqin@china.com

2012-03-02

2012-05-09

1002-8331（2013）21-0216-04

CNKI出版日期：2012-07-16http://www.cnki.net/kcms/detail/11.2127.ΤP.20120716.1501.049.html

◎工程与应用◎