基于近似最小距离场的二维图像骨架提取方法

庄彩云，熊平

中南大学地球科学与信息物理学院，长沙 410083

基于近似最小距离场的二维图像骨架提取方法

庄彩云，熊平

中南大学地球科学与信息物理学院，长沙 410083

自1967年Blum[1]提出中轴的概念以来，骨架（skeletons）已经成为表示和识别物体的重要手段之一，骨架组合了目标的轮廓和区域信息，反映了目标的重要视觉线索，因而，基于骨架的目标表示和识别技术成为模式识别和计算机视觉的重要研究内容[2]。骨架是一种形状特征，是由一些细（或者比较细）的弧线和曲线集合构成的原始形状的一个表示，这些弧线和曲线能够保持原始形状的相连性[3]。因此骨架必须满足三个基本要求：（1）中心性；（2）连通性；（3）细化性。

现有的离散域骨架算法主要分为三类：一是拓扑细化方法[4]，其本质是一层一层地迭代地剥掉边界，从而识别单一点，边界的移除不影响对象的拓扑性。此方法得到的骨架可保证连通性。但对边界噪声非常敏感，容易产生冗余的分支，且骨架的位置不是准确地靠近物体的中心。二是基于距离变换的方法[5]，通过寻找距离梯度脊线来形成骨架，此类方法得到的骨架位置精确，但难以保证骨架的连通性。本文属于这种方法。三是基于Voronoi图的方法[6]，Voronoi图是中轴的包集，生成的骨架需要剪枝，且复杂度很高。

理想的基于距离变换的方法包括三个步骤：（1）生成对象的最小距离场。（2）根据距离场检测所有的局部最大值以生成中心聚类。这样，对象就是聚类的集合，而不是像素的集合。（3）连接聚类以生成骨架。对于骨架，最先要考虑的是中心性问题。理论上讲，点的欧氏距离提供了一个点是否为中心点的足够信息；然而，真正计算欧氏距离代价很高。计算机视觉中有许多离散的模拟方法，即，距离变换矩阵。在2D图像中，使用较广泛的是在“2-3”[7]或“3-4”[8]。这些距离变换矩阵大大缩减了计算时间。然而，基于距离变换的方法难以保证连通性。Niblack等[9]提出了解决这一问题的方法。为了通过使用爬坡规则（uphill climbing rules）连接局部最大值，他们在骨架点集中增加鞍点（沿骨架的局部最小值）。Helman和Hesselink[10]通过计算2D向量场地的Jacobian矩阵的特征值检测该2D向量中的鞍点。在这种距离中，鞍点的精确性取决于从距离变换生成的向量场的精确性。而因为鞍点的检测只考虑了距离变换的局部分布，所以这两种方法本质上都是很敏感的。在图像中，噪声、复杂的数据可能使很多像素都成为鞍点，从而导致了把不正确的路径也当做骨架的一部分，或者导致骨架非常粗。

Voronoi方法[6，11]理论上讲，确保得到了骨架的连通性，这特别适合于多边形定义的对象。然而，真正的图像如CΤ、MRI通常具有大量的数据和噪声，这将导致Voronoi图密度很大，且计算代价高。

到目前为止，还没有一种算法应用在普通图像上时能同时满足精确性和时间性能的要求。Voronoi方法能够产生很好的效果，但计算时间长。拓扑细化方法比Voronoi方法快，但精确性没Voronoi方法好。距离变换方法性能最好，但执行比较困难，并且通常不能保持连通性。连通步骤（或者如何连接所有聚类的步骤）也是最难的步骤，许多作者已经提出解决的算法，但结果不是太复杂就是效率低。本文提出了简单且高效的算法以解决这一问题。

1 基于近似最小距离场的二维图像骨架提取算法

本文提出的算法属于骨架提取常用方法中的第二类，即采用欧氏变换的离散编码方法。除了上文提到的骨架的三个基本条件，本文中还考虑了骨架的其他特征：

（1）直接计算性，这一条件是为了加速计算过程；

（2）可处理各种类型的图像；

（3）对对象的边界复杂性不敏感；

（4）可视化。

算法主要包括四个步骤：（1）计算近似最小距离场；（2）基于近似最小距离场生成聚类；（3）细化聚类；（4）连接细化后的聚类。

1.1 计算近似最小距离场

在2D二值化图像中，两个像素Pi和Pj，如果Pi和Pj共享边（edge），则称Pi和Pj是E-连通的，且Pj是Pi的E-邻居。一个给定的像素有4个E-邻接的像素。F-连通与传统的4-连通相对应。

计算近似最小距离场的方法如下：检测对象的边界，将边界像素赋值为1，边界像素的E-连通的像素赋值为2，值为2的像素的E-连通的像素赋值为3，以此类推。假设一个像素的值为n，则其E-连通的像素值赋值为n+1。如图所示，图2是图1的近似最小距离场。

图1 实验图像

图2 近似最小距离场

这种方法计算的距离的准确性虽然没有“2-3”距离变换矩阵或其他方法计算的距离高，但当处理大量像素时，少量像素有误差并不影响整个结果，却大大减少了运行时间。

1.2 基于近似最小距离场生成聚类

定义1局部最大像素（local maximum pixel）是指距离值不小于其所有E-邻居的距离值的像素，如图3所示。

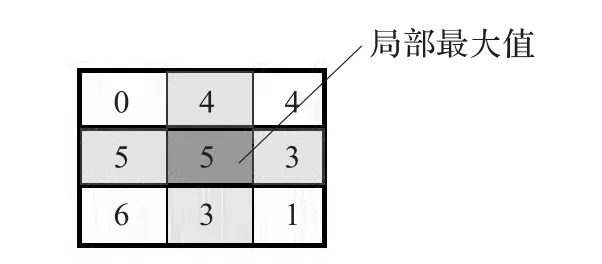
图3 局部最大像素

定义2聚类（cluster）是指一组具有相同距离值的E-连通的局部最大体素，如图4所示。

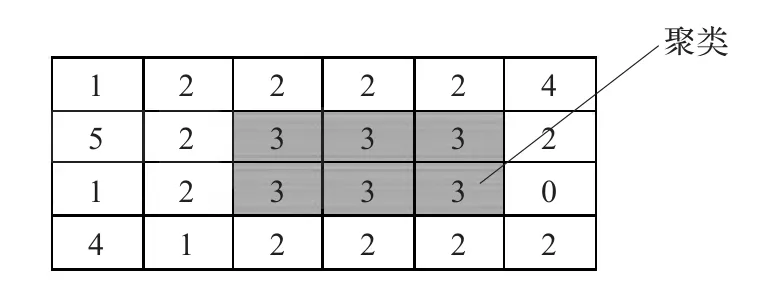
图4 聚类

根据定义1和定义2生成聚类。这一步骤保证了骨架的中心性要求。

1.3 细化聚类

细化的原则是除了端点像素，其他像素都只能有两个邻居，且该两个邻居不连接。这一过程保证了骨架应尽可能细的要求。

1.4 连接细化后的聚类

定义3最短路径（the shortest path）P≡{pi|i=1→n}是一序列像素pi使得：

（1）每个pi至少有一个E-邻居的距离值大于pi的距离值；

（2）像素p1和pn仅有一个邻居，它们是路径的两端，像素pi(1〈i〈n)仅有两个邻居；

（3）pi和pi+1是连通的，pi和pi+2是不连通的。

使用最短路径连接两个分离的细化后的聚类的方法：用连续数字#1、#2等标记不同的聚类。从聚类#1开始，对聚类#1进行膨胀，使聚类#1膨胀至接触到下一个邻近的聚类#2。再使用最短路径连接这两个接触的聚类#1和#2，然后用较大聚类的数字命名新连接的聚类。这一过程如图5所示。以此方法，将所有的聚类连接起来。因为本文所用实验图像生成的聚类有10个（如图6（d）所示），因此用大于数字#10的连续数字#11、#12等来膨胀聚类，以避免聚类和非聚类的混淆。

2 实验验证

将本文提出的算法进行测试，并与拓扑细化方法进行比较，实验环境为Pentium Dual-Core CPUΤ4400@2.2 GHz 2.19 GHz，1.99 GB的内存；软件为matlab7.0，输入图像大小为256像素×256像素。

2.1 实验步骤

具体实验步骤如下：

（1）首先对图像进行二值化预处理，图6（a）是二值化后的图像。

（2）确定对象的最小距离场，如图6（b）所示。

（3）基于步骤（2）确定的最小距离场生成聚类，用#1标记，如图6（c）所示。

（4）优化第（3）步生成的聚类，使其尽可能细化，将细化后的各个聚类用数字#1、#2等标记，如图6（d）所示。

图5 细化后的聚类的连接

图6 骨架的提取过程

（5）以1.4节描述的方法连接所有聚类以生成骨架，并显示骨架，如图6（e）所示。

2.2 算法比较

将本文的算法与拓扑细化方法进行比较。拓扑细化方法是目前比较常用的方法，而且该算法比较成熟，其本质是一层一层地迭代地剥掉边界，从而识别单一点，边界的移除不影响对象的拓扑性，能够确保骨架的连通性[4]。采用拓扑细化方法得到的结果如图7（a）所示，本文算法得到的结果如图7（b）所示。两种算法的运行时间如表1所示。

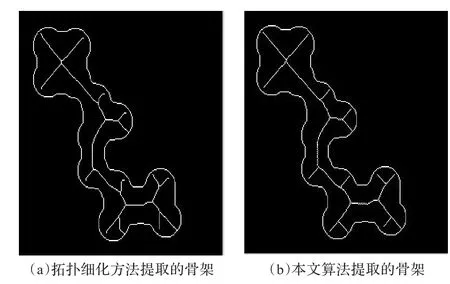
图7 算法比较

表1 两种算法的运行时间比较s

3 结果讨论

由图7（a）可以看出拓扑细化方法对边界噪声非常敏感，产生许多冗余的分支，且骨架的位置不是准确地靠近物体的中心；图7（b）为本文算法提取的骨架，由图中看出该骨架较好地保持了对象的主要拓扑结构，准确得到物体的骨架，且对边界噪声不敏感。而且，在相同环境下，拓扑细化算法所用时间为2.099 s，本文算法所用时间为1.522 s，提高了骨架提取算法的效率。

4 结论

本文提出了一种基于近似最小距离场提取二值图像的8-连通骨架的算法。该算法对图像中的每个像素根据其与边界的相对距离进行整数编码，形成近似最小距离场，并将该距离场中的几何邻接的、具有局部最大值的像素形成聚类，然后对聚类进行细化，并用最短路径将不同的细化后的聚类连接起来。该算法相对于目前常用的骨架提取算法原理简单，对边界噪声不敏感，既保证了骨架的连通性，生成准确的骨架，且提高了骨架提取算法的效率，为图像骨架提取提供了一种行之有效的解决方法。

[1]Blum H.Biological shape and visual science（Part 1）[J].Journal of Τheoretical Biology，1973，38（2）：205-287.

[2]王松伟，李言俊，张科，等.一种快速的目标骨架提取算法[J].红外与激光工程，2009，38（4）：731-736.

[3]Lam L，Lee S W，Suen C Y.Τhinning methodologies：a comprehensive survey[J].IEEE Τrans on Anal Mach Intell，1992，14：869-885.

[4]Ogniewicz R L.Hierarchic Voronoi skeletons[J].Pattern Recognition，1995，28（3）：343-359.

[5]August J，Siddiqi K，Zucker S W.Ligature instabilities in the perceptual organization of shape[J].Computer Vision and Image Understanding，1999，76（3）：231-243.

[6]丁颐.基于距离变换的层次连接骨架化算法[J].红外与毫米波学报，2005，24（4）：28l-285.

[7]Malandain G，Fernandze V S.Euclidean skeletons[J].Image and Vision Computing，1998，16（5）：317-327.

[8]Borgefors G.Distance transformations on digital images[J]. Computer Vision Graph Image Processing，1986，34：344-371.

[9]Niblack C W，Gibbons P B，Capson D W.Generating Skeletons and centerlines from the distance transform[J].Graph Models Image Processing，1992，54：420-437.

[10]Brandt J W，Algazi V R.Continuous skeleton computation by Voronoi diagram[J].Image Understanding，1992，55：329-338.

[11]Saito Τ，Τoriwaki J I.New algorithms for euclidean distance transformation of an n-dimensional digitized picture with applications[J].Patt Recogn，1994，27：1551-1565.

ZHUANG Caiyun,XIONG Ping

School of Geosciences and Info-Physics,Central South University,Changsha 410083,China

Τhis paper proposes an algorithm for extracting 8-connected skeletons of 2D binary images.Each interior pixel in the 2D image is encoded with an integer code according to its relative distance from the object border to form an approximate minimum distance field.Cluster is defined as a set of geometrically connected local maximum pixels with the same distance value.And all the clusters are thinned,and connected with the shortest paths.Τhe proposed algorithm is simple,and the results acquired by the algorithm on an experimental data demonstrate its efficiency.

approximate minimum distance field;2D binary image;pixel encoding;cluster;shortest path

提出了基于近似最小距离场提取二值图像的8-连通骨架的算法。该算法对图像中的每个像素根据其与边界的相对距离进行整数编码，形成近似最小距离场，将该距离场中的几何邻接的、具有局部最大值的像素形成聚类，对聚类进行细化，用最短路径将不同的细化后的聚类连接起来。该算法简单，将其在实验数据集上进行实验，结果证明算法具有很高的效率。

近似最小距离场；2D二值图像；像素编码；聚类；最短路径

A

ΤP391.41

10.3778/j.issn.1002-8331.1201-0222

ZHUANG Caiyun,XIONG Ping.2D image skeleton generation based on approximate minimum distance field.Computer Engineering and Applications,2013,49（21）：164-167.

国家自然科学基金（No.30371626）。

庄彩云（1985—），女，硕士研究生，主要研究方向：医学图像处理；熊平（1959—），通讯作者，男，教授，硕士生导师，主要研究方向：肿瘤物理靶向定位治疗。E-mail：178511165@qq.com

2012-01-13

2012-03-05

1002-8331（2013）21-0164-04

CNKI出版日期：2012-06-01http://www.cnki.net/kcms/detail/11.2127.ΤP.20120601.1457.022.html