一种基于最短路径介数的重要节点发现算法

张珍，张振宇，宋蔓蔓

新疆大学信息科学与工程学院计算机科学系，乌鲁木齐 830000

一种基于最短路径介数的重要节点发现算法

张珍，张振宇，宋蔓蔓

新疆大学信息科学与工程学院计算机科学系，乌鲁木齐 830000

现实世界中存在的大量复杂系统都可以通过各种网络加以描述，例如，因特网、电力网络、病毒网络、罪犯关系网络、谣言传播网络等。在复杂网络的各种基础研究工作中，对网络中节点的重要性进行评估，发掘网络中的重要节点，具有重要的实用价值。对于无标度网络，5%的核心节点被攻击，网络就基本瘫痪[1]。在电力网络中，重要的发电单元若出现故障，将会相继引起大范围的停电[2]。通过节点的重要度评估，找出网络中重要的“核心节点”，一方面可以重点保护这些“核心节点”来提高整个网络的可靠性，另外一方面也可以攻击这些“薄弱环节”达到摧毁整个网络的目的[3]。

1 相关工作

节点的重要性评估方法有很多，目前主要分为社会网络分析、系统科学分析、信息搜索领域分析三大类。社会网络分析方法的一个重要基本思想是，网络中不同节点的重要性差异是通过分析网络中某种有用的信息得到的，例如节点的度、介数、中心接近度、特征向量指标等。其中，利用节点度作为节点重要度的衡量标准[4]是最简单的方法，该方法认为与节点相连的边越多则该节点越重要，但是这种方法容易忽略一些“核心节点”，例如“桥接节点”，作为网络中信息流量很大的节点，它的重要性不能被忽视。文献[5]提出通过节点介数（betweenness centrality）发现网络中的重要节点，但其计算复杂度非常高，为O(n3)。文献[6]定义节点的中心接近度反映了节点在网络中居于中心的程度。节点的中心接近度越大，表明节点越居于网络的中心，它在网络中就越重要。然而，直接使用中心接近度衡量节点的重要性对网络的拓扑结构依赖性比较大。Poulin等人[7]对求解特征向量的映射迭代方法进行了改进，提出了一种累计提名指标，但是这类方法是在保证网络整体性的前提下进行的，具有一定的局限性。系统科学的研究方法是利用网络的连通性来反映系统某种功能的完整性，通过度量节点的删除或融合对网络连通的破坏程度来反应网络节点的重要性。例如，Chen等人[8]提出了一种基于最小生成树的指标，认为最重要的节点是自身及相关链路去掉后使得图的生成树的数目最小的节点。该方法的缺点是如果多个节点的删除都使得网络不连通，那么这些节点的重要性将是一致的，例如“末梢节点”所依附的节点，因而使得评估结果不精确。文献[9]将节点的平均路径和节点的个数乘积的倒数定义为网络凝聚度，用每个节点融合后的网络凝聚度来评价节点重要性，但文中没有描述如何计算节点的平均路径。信息搜索领域的分析方法，主要适用于互联网搜索领域，其中最具有代表性的算法是PageRank算法[10]和HIΤS算法[11]。此后，互联网的搜索领域越来越受到人们的关注，不断有新的算法和变种提出。例如，文献[12]提出的改进方法，即提出了一种基于物理学场论模型的节点排序算法，用节点间的相互作用力来衡量节点之间的转移概率，指向高质量网页的网页节点应该被赋予更大的转移概率，但由于该方法在考虑节点的物质场作用力时主要从两个节点的距离和节点自身的度来衡量，从而忽略了节点在全网内的位置和作用。

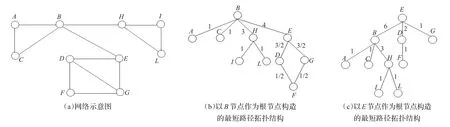
图1 由网络拓扑通过宽度优先遍历构造最短路径拓扑结构

重要节点，即网络中的“枢纽”节点，其反应的是节点在网络中的地位高低或者说是在网络中的影响力大小。本文首先通过最短路径树得到网络中边介数较大的边，由于这些边两端的节点处于许多其他两节点之间的路径上，因此这些节点具有控制其他两个节点之间通信的能力，一个节点在网络中占据这样的位置越多，就代表有越多的节点需要通过它才能与其他节点发生联系，那么该节点在网络中就拥有较大的“权利”，因而最短路径树可以帮助定性地找出在网络中居于重要地位的节点。但此时找到的重要节点的重要性相同，在现实网络中，由于自然经济、社会条件的差异，重要节点之间仍然会表现出重要性的差异。本文使用中心接近度来定量地分析这些重要节点的重要性，中心接近度刻画的是节点的中心指数，它衡量了网络中节点与其他节点联系的多少，如果一个节点通过比较短的路径与许多其他节点相连，那么该节点就具有较高的中心接近度。总结来说，本文的方法首先通过边介数来衡量网络中节点“控制”其他节点的能力，然后对找到的重要节点通过中心接近度来衡量这些节点不受其他节点“控制”的能力，最后得出网络中重要节点的排序。

本文首先介绍了基于最短路径介数发现重要节点的算法设计，然后描述了使用中心接近度评估节点的重要性，最后通过案例分析验证了该方法的有效性。

2 算法设计

2.1 算法描述

（1）基于最短路径介数发现重要节点

文献[13]通过最短路径介数发现网络中“流量”最大的边，该方法的基本思想是以网络中每个节点作为根节点通过宽度优先遍历构造其与其他节点的最短路径拓扑结构并计算边上的权值，权值表示网络中经过该边可达的某个节点的最短路径占可到达该节点的所有最短路径总数的比例之和。原始网络中每条边的边介数等于构造的所有最短路径拓扑结构上该边的权值之和，如图1所示。

通过计算，图1（a）中边介数最大的边是BE，应当删除BE边。删除BE后原始网络拓扑结构发生变化，继续构造最短路径拓扑结构找出第二条可以删除的边介数最大的边。文献[10]提出算法终止条件，即最优的聚类划分结果是当模块Q函数的Q值达到最大时的划分结果，通过计算得出第二次删除边BH后Q值达到最大，算法终止。因此，划分过程中删除的边是BE、BH。

根据图1（a）中的网络拓扑结构，计算了所有节点的点介数，如表1所示。从表中可以看出，节点B、E、H的点介数较之其他节点较大，说明节点B、E、H在网络中的流量较大，即在网络中的地位越重要。因此，通过最短路径介数的方法找到边介数最大的同时也可以发现网络中比较重要的节点，这样大大降低了直接计算节点介数的复杂度。此时发现的节点B、E、H的重要性相同。

表1 节点介数的计算

（2）用中心接近度评估重要节点的重要性

2.2 算法流程

对于已知的网络拓扑结构图G，可以直接输入邻接矩阵A完成初始化。令m表示图的边数，n表示图的节点数，矩阵B存储节点对之间的边介数，链表Q和K分别存储模块化Q值和重要节点，其中Q0=0，链表C存储重要节点的中心接近度。本文算法可以简单描述如下：

输入：G的邻接矩阵A

输出：重要节点排序结果

步骤1发现网络中的重要节点

以当前节点作为根节点通过宽度优先遍历构造最短路径拓扑结构；

步骤2计算重要节点的重要性

2.3 计算复杂度分析

从上述算法流程看，整个算法的计算复杂度取决于步骤1通过最短路径拓扑结构求出网络中介数最大的边及步骤2计算中心接近度，对于步骤1文献[9]中给出的最坏情况下的计算复杂度为O(m2n)，对于步骤2采用Dijstra算法计算复杂度为O(n2)。因此，整个算法的计算复杂度为O(m2n+kn2)，考虑到现实网络中，k远远小于n，一般情况下，算法的计算复杂度〈〈O(m2n+n3)。

3 实验

3.1 实验条件及方法

实验采用真核细胞新陈代谢网络[14]中的一个网络模块，如图2所示。该模块有30个节点，34条边，其中节点代表蛋白质，若两个蛋白质参与了同一活动，则它们之间存在一条边。对该模块分别采用文献[4]、文献[5]、文献[10]、文献[12]以及本文方法求出全网中最重要的节点，实验结果见表2。

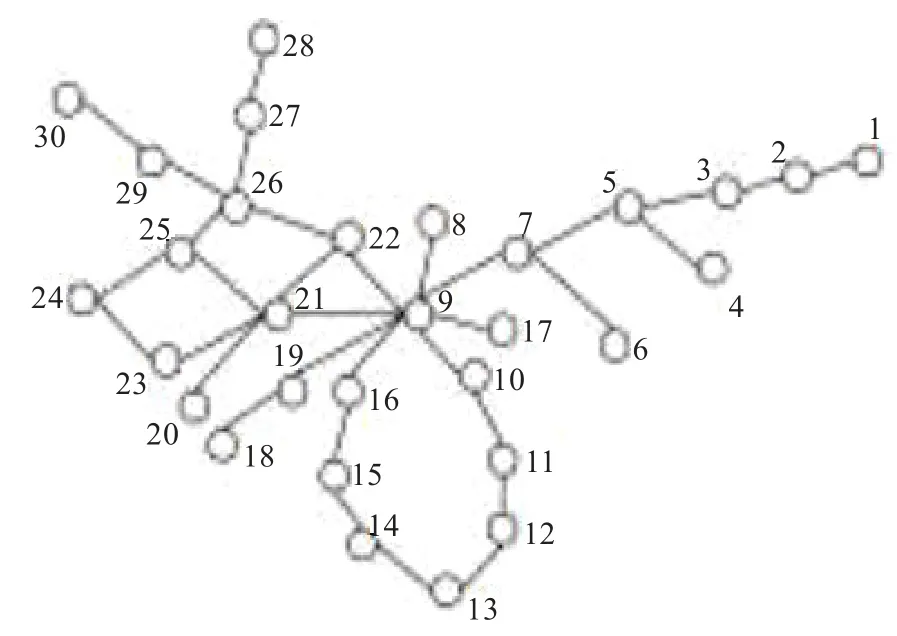
图2 真核细胞新陈代谢网络中的一个模块

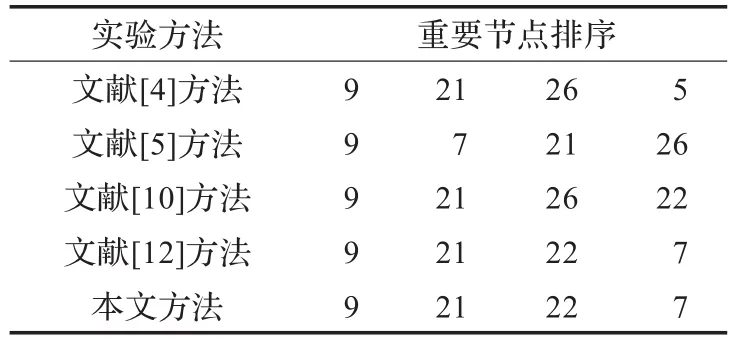
表2 使用四种方法计算重要节点的排序

3.2 实验结果及分析

由表2可以看出，本文算法与文献[4]、文献[5]的方法得出的结果不相同，原因在于本文方法不仅考虑了节点的介数，同时又考虑到了节点在网络中的位置。而本文算法与文献[12]的算法计算出的排名第三的节点是22，文献[10]Pagerank算法计算出排名第三的节点是26，区别在于虽然节点22的度没有节点26的度大，但文献[12]认为节点22跳向9的概率更大，本文方法认为节点22比节点26更趋向于网络中心。综上所述，本文的算法具有很好的参考价值。

4 总结

本文提出了一种基于最短路径介数及节点中心接近度的网络重要节点及其重要性的发现算法。该方法综合考虑了节点的网络流量和节点位置，可以准确发现全网内的重要节点及其重要性。由于无需对网络中的全部节点的重要性进行评估，大大缩减了计算时间，在保证精确性的同时克服了直接计算节点介数的复杂性，提高了效率。

[1]Wang Xun，Ling Yun，Fei Yulian.Personalization recommendation system based on web log&cache data mining[J]. Journal of the China Society for Scientific and Τechnical Information，2005，24（3）：324-328.

[2]赫南，李德毅，淦文燕，等.复杂网络中重要性节点发掘综述[J].计算机科学，2007（12）.

[3]谭跃进，吴俊，邓宏钟.复杂网络中节点重要度评估的节点收缩方法[J].系统工程理论与实践，2006，11（11）：79-83.

[4]Callaway D S，Newman M E J，Strogatz S H.Network robustness and fragility：percolation on Randon graphs[J].Physical Review Letters，2000，85（25）：5468-5471.

[5]Freeman L C.A set of measures of centrality based upon betweenness[J].Sociometry，1977，40（1）：35-41.

[6]Sabidussi G.Τhe centrality index of a graph[J].Psychometrika，1966，31：581-603.

[7]Poulin R，Boily M C，Masse B R.Dynamical systems to define centrality in social networks[J].Social Networks，2000，22：187-220.

[8]Chen Y，Hu A Q，Hu J，et al.A method for finding the mostvitalnodeincommunicationnetworks[J].High Τechnology Letters，2004，1：573-575.

[9]Wu J，Τan Y J.Finding the most vital node by node contraction in communication networks[C]//2005 IEEE International Conference on Communications，Circuits and Systems Proceeding，Changsha，2005：1283-1286.

[10]Horowitz D，Kamvar S D.Τhe anatomy of a large-scale social search engine[C]//Τhe International World Wide Web Conference Committee，2010：26-30.

[11]Agichtein E，Brill E，Dumais S.Improving web search ranking by incorporating user behavior information[C]//Proc of the 29th Annual International ACM SIGIR Conf on Research and Development in Information Retrieval，2006.

[12]何建军，李仁发.改进的随机游走模型节点排序方法[J].计算机工程与应用，2011，47（12）：87-89.

[13]Newman M E J，Girvan M.Finding and evaluating community structure in networks[J].Physical Review E，2004，69.

[14]Guimera R，Sales P M，Lan A.Classes of complex networks defined by role-to-role connectivity profiles[J].Nature Physics，2007，3：63-69.

ZHANG Zhen,ZHANG Zhenyu,SONG Manman

Department of Computer Science,School of Information Science and Engineering,Xinjiang University,Urumqi 830000,China

Finding important nodes in network is one of the most important topics of studying the properties of network,which is widely used in complex network,system science,analysis of social network and searching in Internet.In order to improve efficiency and effectiveness of finding important node,a new algorithm based on shortest-path betweenness and closeness centrality is presented.It ensures important nodes in the whole network by using the shortest-path betweenness,analyses the importance of important nodes by using the closeness centrality.Compared with the current approach,the results obtained from performance analysis show the algorithm is a feasible and efficient approach for finding important nodes in large-scale P2P networks.

important nodes;shortest-path betweenness;closeness centrality;complex networks;network topology

网络中重要节点的发现是研究网络特性的重要方面之一，在复杂网络、系统科学、社会网分析和互联网搜索等领域中具有广泛的应用价值。为提高全网范围内重要节点发现的效率和有效性，提出了一种基于最短路径介数及节点中心接近度的重要节点发现算法，通过最短路径介数的方法确定全网内的重要节点，利用中心接近度分析重要节点的重要性。测试结果表明，与同类的系统比较起来，该方法具有比较好的性能。

重要节点；最短路径介数；中心接近度；复杂网络；网络拓扑

A

ΤP393

10.3778/j.issn.1002-8331.1201-0307

ZHANG Zhen,ZHANG Zhenyu,SONG Manman.Important node searching algorithm based on shortest-path betweeness. Computer Engineering and Applications,2013,49（21）：98-100.

张珍（1988—），女，硕士研究生，主要研究方向为网络拓扑结构与信息安全；张振宇（1964—），男，副教授，硕士导师，主要研究方向为计算机应用及信息处理、网络拓扑结构与信息安全；宋蔓蔓（1987—），女，硕士研究生，主要研究方向为网络拓扑结构与信息安全。E-mail：zhangzhen_2013@126.com

2012-01-16

2012-04-10

1002-8331（2013）21-0098-03