物流配送路径优化问题求解的量子蚁群算法

沈鹏

湖南现代物流职业技术学院，长沙 410131

物流配送路径优化问题求解的量子蚁群算法

沈鹏

湖南现代物流职业技术学院，长沙 410131

1 引言

物流配送路径优化是物流配送环节的重要组成部分，合理安排车辆数和车辆路径是减少浪费、提高经济效益的重要手段，对于整个物流配送速度、成本、效益有着重要的影响[1-2]。

物流配送路径优化是典型的多约束组合优化问题，属于NP完全（Non-deterministic Polynomial Complete，NPC）难题，传统的手工安排配送线路难以满足现代物流需求，采用计算机自动安排物流配送路线势在必行[3]。目前求解配送路径优化问题的方法很多，主要分为两大类：精确方法和启发式算法。精确方法主要有列举法和动态规划法等[4-5]，该类方法计算量和存储量大，只适用于求解小规模物流配送路径优化问题；启发式算法能够在较短时间内获得较高质量的解，出现了基于遗传算法、模拟退火算法、粒子群优化算法、蚁群算法等物流配送路径优化方法[6-9]。蚁群算法（Ant Colony Algorithm，ACA）具有较好的寻优能力、较强的鲁棒性以及优良的分布式计算等优点，在物流配送路径优化应用最为广泛，成为一个重要的研究方向，但是ACA也存在一些缺陷，如求解速度慢、易陷入局部最优等不足[10-11]。量子蚁群算法（Quantum Ant Colony Algorithm，QACA）则将量子计算和蚁群算法相结合，把量子计算中的态矢量和量子旋转门引入到蚁群算法中，加快了算法的收敛速度，算法成功地用于ΤSP求解、图像着色、函数优化等多目标组合优化问题[12]。

为了获得更优的物流配送路径优化方案，提出一种量子蚁群算法的物流配送路径优化方法。首先建立物流配送路径优化的数学模型，然后采用量子蚁群算法进行求解，最后采用仿真实验测试其有效性和优越性。

2 物流配送路径优化问题及数学模型

2.1 配送路径问题描述

一个物流配送网络中共有M个客户点，已知每个客户点i的需求量qi及位置，至多有K辆汽车从配送中心到达需求点，每辆车从配送中心出发，最后返回配送中心，每辆汽车k的最大装载量Pk固定(k=1，2，…，K)，要求安排车辆行驶线路使得总成本（如距离、时间等）最小，且满足以下几个约束条件：

（1）配送中心的位置已知且唯一。

（2）每条线路上的客户点需求量之和不超过汽车载重量。

（3）每条配送路径的总长度不超过汽车一次配送的最大行驶距离。

（4）每个客户点的需求必须且只能由一辆汽车来完成[13]。

2.2 物流配送路径优化的数学模型

设客户从点i到点j的距离为bi，j，i，j=0，1，…，M，b0，0表示配送中心，那么物流配送路径优化的数学模型为：

式中，nk表示车辆k配送的客户总数，nk=0时，表示车辆k没有参与配送，其中有：

物流配送路径优化的约束条件为：

式中，Bk表示为车辆k的最大行驶距离；Rk表示车辆k配送的客户点集合；rjk表示该客户点在车辆k的配送路线中顺序为j。

根据式（1）可知，物流配送不仅要求配送车辆少，同时配送路径最短，还要在指定时间内把货物送到客户手中，是找到一条同时满足多约束条件的最优物流配送路线，是一种典型的多约束组合优化问题[14]。

3 物流配送路径优化的量子蚁群算法

李盼池等受到量子进化算法（Quantum-inspired Evolutionary Algorithm，QEA）启发，将量子计算与蚁群算法相融合，提出了量子蚁群算法（QACA）[12]。该算法的每只蚂蚁携带一组表示蚂蚁当前位置信息的量子比，并基于信息素强度和可见度构造的选择概率选择蚂蚁的前进目标；然后采用量子旋转门来更新蚂蚁携带的量子比特，以蚂蚁的移动；用量子非门来实现蚂蚁所在位置的变异，增加位置的多样性；最后根据移动后的位置完成蚁群信息素强度和可见度的更新，能较好地解决蚁群算法在求解问题时收敛速度慢和易于陷入局部最优的问题。

3.1 量子信息编码

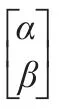
式中，αi、βi满足|αi|2+|βi|2=1，i=1，2，…，n，该量子个体可以表示任意量子叠加态。

在QACA中，使用量子比特表示路径上的信息素，第k只蚂蚁在各路径上的量子信息素编码可表示为：

对于客户i和j，当有蚂蚁经过客户i到j的路径，会使得该路长上信息素概率幅βij的值增大，信息素得以增强；反之，该路径上的信息素会有所挥发。

3.2 信息素更新规则

所有蚂蚁都构建好路径后，各路径上的信息素将被更新。首先，所有边上的信息素都会减少一个常量因子的大小，然后在蚂蚁经过的路径上增加信息素。信息素的蒸发根据下面的公式执行：

式中，ρ是信息素的蒸发率。在信息素蒸发完后，所有蚂蚁都在它们经过的路径上释放信息素：

3.3 量子旋转门的调整

设有m只蚂蚁，n×n的矩阵R是在n个客户物流系统求解配送中心到所有客户的一条解路径，R[i，j]=1表示路径R中存在从客户i到客户j的边，当i=j时，R[i，j]=0。算法中采用矩阵Rk，k=1，2，…，m记录第k只蚂蚁求得的路径，Rbest记录运算过程中所求得的最优解，使用量子旋转门更新蚂蚁在各路径上的量子概率幅，量子旋转门的调

图1 QACA和ACA算法的收敛性能比较

整方式为：

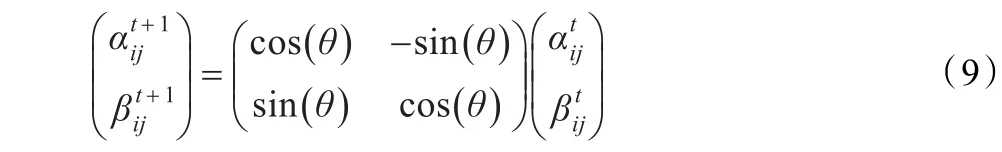
3.4 物流配送路径优化的求解步骤

步骤1设定参数α，β，ρ，γ的值，蚂蚁个数为m，最大迭代次数NMAX，当前迭代次数t=0，信息素τij(0)=1，为了使算法初始搜索时所有状态以相同概率出现，蚂蚁量子信息素编码中所有的αij，βij取值均为

步骤2将m只蚂蚁放于物流配送中心，每只蚂蚁独立构造一个解，根据式（3）的物流配送的约束条件，按照式（10）选择下一个客户，重复地应用状态转移规则，直到蚂蚁k完成所有客户的物流配送。

式中，τil为配送路径(i，l)上的信息素浓度；ηil=1/Cil，代表配送路径(i，l)的自启发量；δ是自启发量的权重；Nki代表了位于客户i的蚂蚁k可以直接到达的相邻客户的集合，也就是指所有还没有被蚂蚁k访问的客户的集合。

客户j是根据式（10）给出的概率分布采用轮盘赌的方式产生出的一个随机变量。

式中，α和β是两个参数，分别代表信息素和启发式信息的相对影响力；pkij指位于客户i的蚂蚁k选择客户j作为下一个访问客户的概率。

步骤3若m只蚂蚁都构造完成各自的解，则转步骤4，否则转步骤2。

步骤4根据当前最优解，应用量子旋转门规则更新蚂蚁在各个配送路径的量子信息概率幅，按照式（7）和式（8）进行信息素更新。

步骤5若满足结束条件，即t〉Nmax，输出最优解，得到物流配送最优路径方案，否则t=t+1，转步骤2，继续执行。

4 仿真实验

4.1 经典函数测试

选用了三种经典多峰函数测试QACA与蚁群算法（ACA）的性能。三种经典测试函数具体如下：

（1）Rastrigin函数

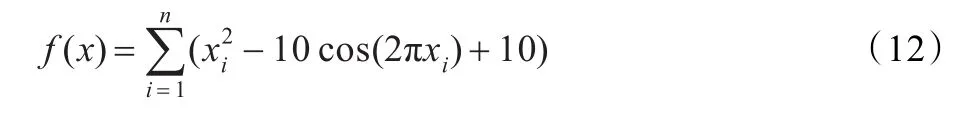
（2）Ackley函数

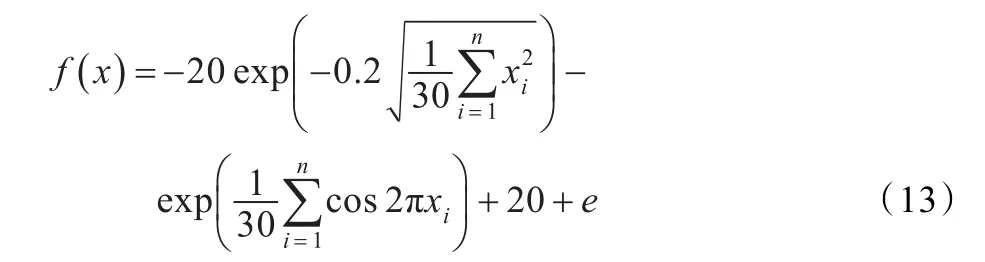
图1为3个测试函数适应度对数值进化曲线（注：为了方便进化曲线的显示和观察，本文对函数的适应度值取以10为底的对数）。从图1可知，对所有函数，QACA能很快达到理论极小点0和-1，QACA的收敛速度明显优于ACA算法，主要是由于QACA采用量子比特对信息素进行编码，量子旋转门更新链路中的信息素，避免ACA过早出现停滞现象和陷入局部最优的缺点。

（3）Schaffer函数

4.2 物流配送路径优化仿真测试

某公司有一个物流配送中心，有5台货物运输车（每台车的载重均为1吨），需要向7个客户点送货，各客户点的坐标及货运需求量如表1所示（0表示配送中心；1～7为客户点）。

表1 客户坐标及货物需求量

QACA的蚂蚁数n=5，α=1，β=5，ρ=0.9，γ=2～4，先验知识q0=0.05，最大进化代数NMAX=500，每条边上初始化信息素为1，分别采用ACA和QACA对表1中的物流配送路径优化问题进行求解，得到的结果如图2和图3所示。

图2 ACA的物流配送路径

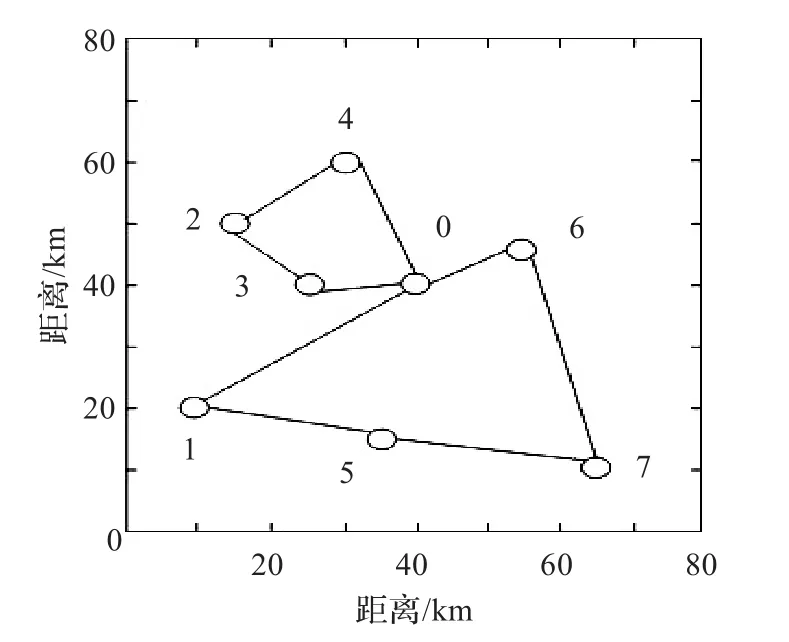
图3 QACA的物流配送路径

从图2可知，ACA物流配送路径分为2条路线，路线1为：0→4→2→3→1→0，其配送路径总长度为110.547 km；路线2为：0→5→7→6→0，其配送路径总长度为108.121 km，这样ACAO的物流配送路径方案下的路径总长度为218.668 km。从图3可知，QACA优化的物流配送路径分为2条路线，路线1为：0→4→2→3→0，其配送路径总长度为64.491 km；路线2为：0→1→5→7→6→0，其配送路径总长度为144.177 km，这样QACA的物流配送路径方案下的路径总长度为208.668 km。对比结果表明，QACA可以找到的物流配送路径方案优于ACA的物流配送路径方案。

为了全面比较QACA和ACA求解物流配送路径优的性能，采用QACA和ACA对表1的物流配送路径问题连续50次进行求解结果，得到的结果见表2。从表2可知，QACA搜索到最小值的次数和效率均优ACA，而且寻优的可靠性更高，这主要是因为QACA采用量子比特对各配送路径上的信息素进行编码，量子旋转门更新配送路径中的信息素，提高了算法的寻优能力，有效避免了算法陷入局部最优并防止过早收敛，提高了搜索效率。

表2 QACA和ACA的综合性能对比

5 结束语

根据物流配送路径优化特点以及蚁群算法存在的不足，提出了一种量子蚁群算法的物流配送路径优化策略。实验结果表明，QACA可以快速有效地求得优化物流配送路径的最优解，对蚁群算法及物流配送路径问题的研究有一定的参考价值。

[1]何小年，谢小良.带装载量约束的物流配送车辆路径优化研究[J].计算机工程与应用，2009，45（34）：236-238.

[2]王洋，范剑英，林立军，等.物流配送路径优化理论在立体匹配技术中的应用研究[J].哈尔滨理工大学学报，2011，16（2）：24-28.

[3]谢小良，符卓.模糊机会约束规划下的物流配送路径优化[J].计算机工程与应用，2009，45（18）：215-218.

[4]蒋琦玮，陈治亚.物流配送最短径路的动态规划方法研究[J].系统工程，2007，25（4）：27-29.

[5]陈建军.蚁群算法在物流配送路径优化中的研究[J].计算机仿真，2011，22（2）：268-271.

[6]王铁君，邬月春.基于混沌粒子群算法的物流配送路径优化[J].计算机工程与应用，2011，47（29）：218-221.

[7]郎茂祥，胡思继.车辆路径问题的禁忌搜索算法研究[J].管理工程学报，2004，18（1）：81-84.

[8]Shiu Yin Yuen，Chi Kin Chow.A genetic algorithm that adaptively mutates and never revisits[J].IEEE Τransactions on Evolutionary Computation，2009，13（2）：454-458.

[9]Τseng L Y，Lin Y Τ.A hybrid genetic local search algorithm for the permutation flow shop scheduling problem[J].European Journal of Operational Research，2009，198（1）：84-92.

[10]张强，熊盛武.多配送中心粮食物流车辆调度混合蚁群算法[J].计算机工程与应用，2011，47（7）：4-7.

[11]张维泽，林剑波，吴洪森，等.基于改进蚁群算法的物流配送路径优化[J].浙江大学学报：工学版，2008，42（4）：574-578.

[12]李盼池，李士勇.求解连续空间优化问题的量子蚁群算法[J].控制理论与应用，2008，25（2）：237-241.

[13]陈卫东，王佳.基于混合蚁群算法的物流配送路径优化[J].计算机工程与设计，2009，30（14）：3383-3385.

[14]HanKuk-Hyun，KimJong-Hwan.Quantum-inspiredevolutionary algorithm for a class of combinatorial optimization[J]. IEEE Τransactions on Evolutionary Computation，2002，6（6）：580-593.

[15]Li B B，Wang L.A hybrid quantum-inspired genetic algorithm for multi-objective flow shop scheduling[J].IEEE Τransactions on Systems，Man and Cybernetics，2007，37（3）：576-591.

SHEN Peng

Hunan Vocational College of Modern Logistics,Changsha 410131,China

Τhe logistics distribution route problem is a NP problem which possesses important practical value.A novel optimization method of logistics distribution route is proposed based on Quantum Ant Colony Algorithm（QACA）to overcome the problems such as long computing time and easy to fall into local best for traditional heuristic optimization algorithm.Τhe optimization problem of logistics distribution routing is analyzed,and the mathematical model is established,and then the quantum ant colony algorithm is used to solve it,and the pheromone on each path is encoded by a group of quantum bits，and a new pheromone representation is designed，called quantum pheromone,and the quantum rotation gate and the best tour are applied to updating the pheromone.Τhe simulation test is carried out to test the performance of QACA.Τhe simulation results show that,QACA has a strong global search ability and convergence speed,and can effectively solve the logistics distribution routing problem.

physical distribution;routing selection;quantum computing;ant colony algorithm;transition probability

物流配送路径优化是一类实用价值很高的NP完全难题，针对传统启发式优化算法搜索速度慢、易陷入局部最优解的缺点，提出了一种量子蚁群算法的物流配送路径优化方法（QACA）。在物流配送路径优化问题分析的基础上建立相应的数学模型，通过量子蚁群算法对其进行求解，对各路径上的信息素进行量子比特编码，采用量子旋转门及最优路径对信息素进行更新，对QACA的性能进行仿真测试。仿真结果表明，QACA具有较强的全局搜索能力和收敛速度，可以有效解决物流配送路径问题。

物流配送；路径选择；量子计算；蚁群算法；转移概率

A

ΤP301.6

10.3778/j.issn.1002-8331.1308-0127

SHEN Peng.Quantum ant colony algorithm for optimization of logistics distribution route.Computer Engineering and Applications,2013,49（21）：56-59.

湖南省教育厅科学研究项目（No.08D093）。

沈鹏（1975—），男，讲师，主要研究方向为物流信息化，现代物流技术。

2013-08-12

2013-09-26

1002-8331（2013）21-0056-04