基于UDCT系数的改进HMT和在图像去噪中应用
杨兴明,陈海燕,王 刚,王彬彬,赵银平
1.合肥工业大学 计算机与信息学院,合肥 230009
2.合肥工业大学 电气与自动化工程学院,合肥 230009
基于UDCT系数的改进HMT和在图像去噪中应用
杨兴明1,陈海燕1,王 刚1,王彬彬1,赵银平2
1.合肥工业大学 计算机与信息学院,合肥 230009
2.合肥工业大学 电气与自动化工程学院,合肥 230009
1 引言
图像处理的应用非常广泛,例如去噪、融合、分割等[1-2],图像噪声去除的基本方法有空间域的和变换域的,空间域滤波能够有效滤除光滑区域的噪声但容易模糊边缘;变换域去噪的方法主要由傅里叶变换和小波变换,而小波变换由于其多分辨率和时频局部等特性,广泛用于图像去噪。由两个一维正交小波基张成的二维小波具有各向同性使其在表示图像边界时候不具有稀疏性,不是最优基。
沿图像的曲线边缘表示是图像表示的一个突破。自2000年以后常用的方法有:曲波变换(Curvelet),轮廓波变换(Contourlet)等。Curvelet变换在描述二次光滑空间的曲线时具有独到的优势,其通过幅度窗口函数和角度窗口函数实现对图像曲线的完美重构,并且Curvelet变换的快速变换(Fast Discrete Curvelet Transform,FDCT)在频率域使用FFT算法实现的[3]。Contourlet变换是在空间域通过滤波器组结构实现的参数化Curvelet变换,故Contourlet基函数不是带限的[4]。Truong T.Nguyen和Hervé Chauris提出均匀离散曲波变换(UDCT)结合了Curvelet变换和Contourlet变换的优点:它是通过在频域用类似Contourlet结构的多分辨率滤波器组实现的;UDCT频率域的滤波器组的构造是满足Curvelet基函数要求;故UDCT既具有Curvelet完整的理论基础也有类似于Contourlet的易于实现滤波器组结构[5]。UDCT和折叠FDCT一样都是使用FFT算法实现的,但是二者的区别是:UDCT采用滤波器组结构下的采样来降低冗余率,而折叠FDCT是通过频率域的对频率进行折叠来降低冗余率的;UDCT基函数是在均匀的整数网格中的,而FDCT基函数是在非均匀网格中;UDCT系数具有和小波系数一样的树结构而折叠FDCT系数则不具有树的结构。
HMT能很好地描述这种具有树结构系数之间的关系。四叉树建立每个父系数和其四个子系数之间的隐状态联系。关于Wavwlet HMT模型和Contourlet HMT模型已有大量研究并且都证明其具有良好的去噪效果[6-7]。本文将HMT模型应用到UDCT系数上,实验证明:该模型具有良好的去噪效果。
2 均匀离散曲波变化(UDCT)的实现
均匀离散曲波变换(UDCT)是可逆多分辨率变换,是在频率域通过类似Contourlet滤波器组结构实现的。实现过程如图1示。

图1 UDCT的正变换和反变换
在频域将用到类似Contourlet滤波器组的参数化窗口,可以表示为有1个低通和2N个方向高通的二维滤波器组。在不同的分辨率下通过级联相同的滤波器组,即是UDCT频域离散分解。定义2-D参数化窗口函数族构成式(1)的单位分解;当N=3时,7个窗函数定义的如式(2)7带滤波器组。

其中u0(ω)为离散低通滤波器频率响应,ul(ω)为6个2-D方向滤波器组频率响应,l为方向个数。
在空间域,合成滤波器gl(n)和分解滤波器是一样的,gl(n)=fl(n),抽取比率依然是2I,在滤波器的输出端,重构图像是用傅里叶逆变换得到UDCT系数的实部进行重构的,如图2。

图2 UDCT频域完全重构滤波器组

3 UDCT系数统计特性分析
研究UDCT系数的统计特性首先要研究系数实部和虚部边缘分布和联合分布。对Lena图像进行4层分解,取最细节的一个方向子带,统计其系数的实部和虚部的概率统计和联合分布如图3示。
计算系数实部和虚部分布的峰值系数kurtosis分别为84.11和50.44,得到子带内的系数的实部和虚部都是呈非高斯分布的特性。UDCT系数的实部和虚部是零均值、不相关、同变性。从图3(c)中可以看出系数的实部和虚部关于圆点呈中心对称分布的,复系数的概率密度函数只和系数的大小有关。
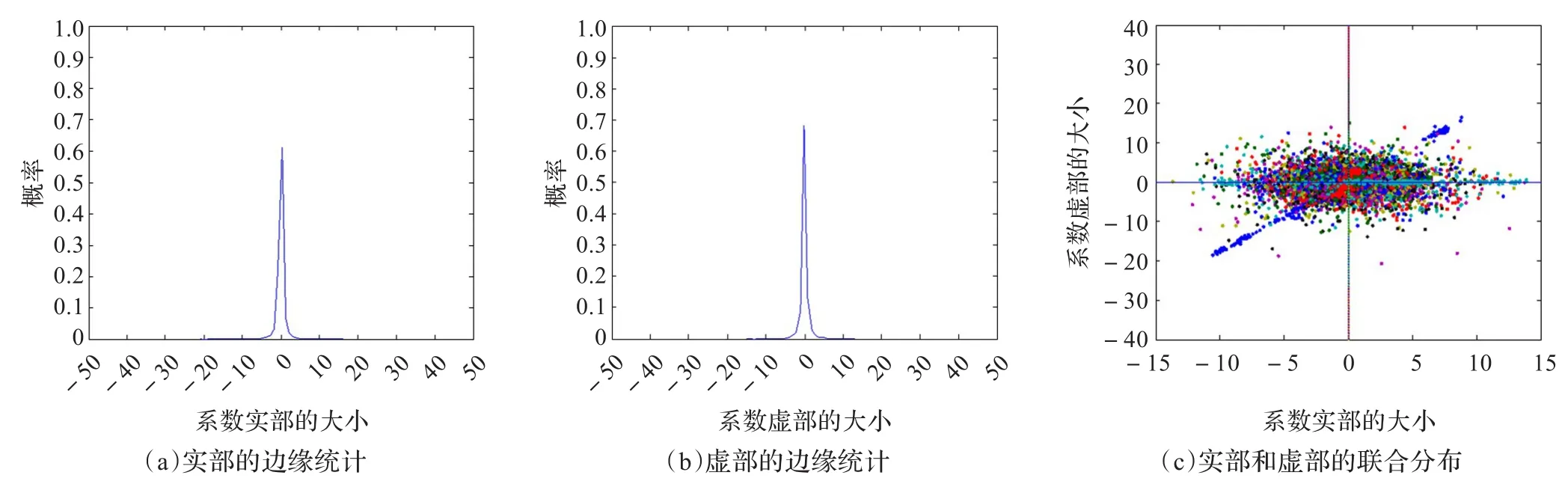
图3 Lena高频子带系数边缘统计和联合分布
同时,还需要对尺度间的系数的关系进行研究,系数X的邻系数集包括:其上尺度的父系数(parentPX)、同一尺度内的邻系数(neighborNX)和同一尺度的不同方向子带的方向系数(cousinCX),如图4所示。对Lena图像进行UDCT后得到的系数,选取一个细尺度系数X,在已知父系数情况下实部和虚部的Kurtosis分别为:4.12和3.95,所以,在已知父系数PX的条件下,系数X实部和虚部的分布可以用高斯混合分布进行建模。
4 基于信息理论系数依赖性分析
考察系数X和其PX,NX,CX的依赖性强弱,可以通过计算系数之间的互信息量。X和Y的互信息表示Y从X那得到的信息的多少,当X,Y独立时,互信息量为0,当X=Y时,互信息量最大为1。X,Y的互信息的定义如下:

其中,fX(x),fY(y)分别为X,Y的边缘概率密度函数,fXY(x,y)为X,Y联合概率密度函数。实际中用直方图结合熵和互信息中的方法计算I(X;Y)[8]。互信息量常被用于小波域和曲波域来评价系数的相关性[9-10]。由于UDCT系数的实数部分和虚数部分具有相似的性质,这里仅研究系数X的实数部分和其PX、NX、CX的互信息量,如表1所示。

表1 系数X和其邻系数PX、NX、CX的互信息量
从表1中,可以看出:

子带内系数之间的相关性具有对其他相关性的主导性。即:X服从什么分布和NX的依赖性最大的,这和已得的小波系数和曲波系数的依赖性结果是一致的[9]。
5 UDCT系数的HMT模型
5.1 UDCT系数的HMT模型建立
由第二、第三部分讨论得出的UDCT系数在已知父系数PX的条件下,系数X实部和虚部的分布可以用高斯混合分布进行建模的条件高斯特性和系数间的依赖性关系,选择HMT进行建模。首先进行UDCT进行4层分解,每一层的方向分别为:6、6、12、12,对其建立如图4(c)的多树模型。
图4(a)所示的是Wavelet系数的父子关系,每一个小波系数的子系数只能在一个子带内,图4(b)中UDCT系数的子系数可以在两个子带中,在图4(c)中树的第三层中可以看出两个子带对应于一个父系数。
对于在尺度j,方向k位置n的系数记为c(j,k,n),其相应的隐状态为S(j,k,n),值为L,S分别代表具有此状态的系数是服从大的方差和小的方差的分布。当S(j,k,n)=L对应的分布的均值和方差,当值为S时,对应分布的均值和方差分别为。则UDCT系数的概率密度函数为:

其中,UDCT系数为零均值的,则
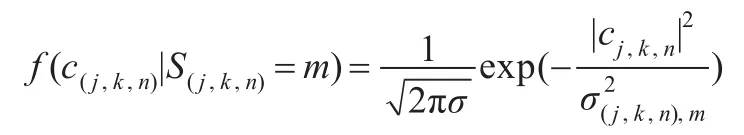
P(S(j,k,n)=m)表示系数s(j,k,n)是状态m(L,S)的概率,

5.2 模型参数的初始化和估计
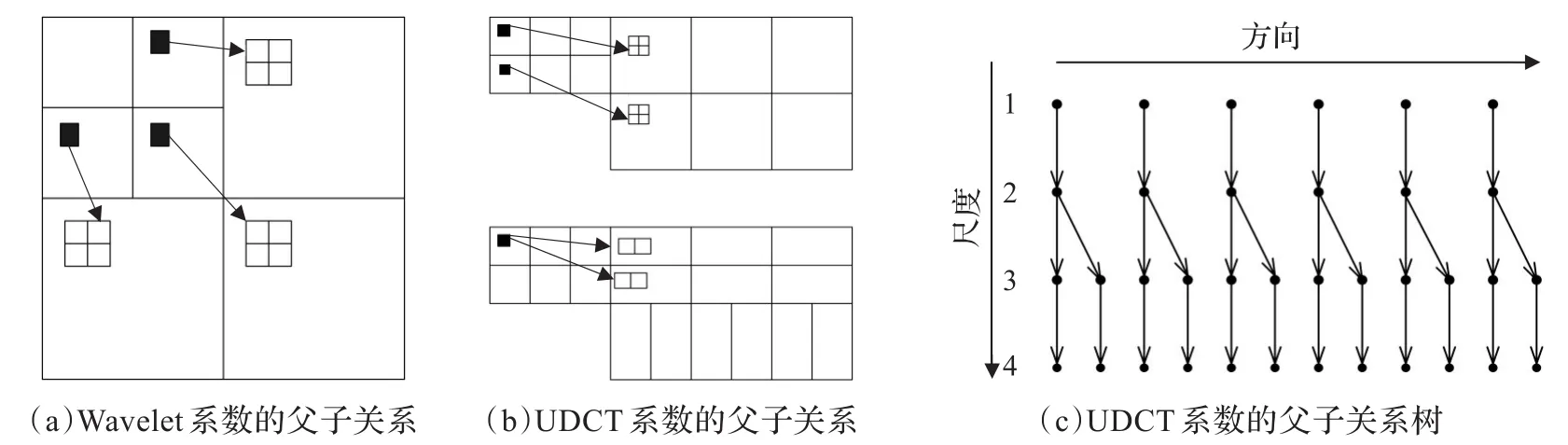
图4 Wavelet系数和UDCT系数父子关系
用EM算法对UDCT系数的HMT模型的参数估计,该算法估计的参数在图像去噪中取得非常好的效果,但是该算法由于计算量庞大导致运算时间较长,不利于对时间要求比较高的应用,针对这个问题,可以通过选择合适的初始参数来减小运算时间[11]。通过研究UDCT系数的延续性,发现其具有规律性。以图4(c)为例,UDCT分解层数为4层,6个方向,分别建立了6棵树,不同层,同层不同方向子带的状态转移概率是不同的,即:若原来父系数是服从大方差分布的但是其子系数是符合大方差还是小方差分布的概率和其所在的分解层数有关的;UDCT系数在高频上具有很强的方向性,随着尺度的增加,小系数产生小系数的概率不断增加,到一定的尺度之后,边界被完全分开只剩下平滑的区域,则小系数产生小系数的概率趋向于1,边界在任一高分辨率子空间可能存在也可能消失,不存在边界的高分辨率子空间的UDCT系数值较小,故大系数产生大系数的概率逐渐趋向于1/2。在中间层,由于UDCT函数的方向性,边界没有完全分开,出现大小系数的概率是差不多的。状态转移概率是用来刻画UDCT系数的尺度间的延续性的,考察的是子带与其父子带的状态概率的关系。为了研究这种关系,可以用子带和其父带的各状态的统计来揭示它们的状态概率的关系。由于用高斯混合模型来模拟UDCT系数的“大”、“小”状态,则根据UDCT变换的特点,用一个自适应的阈值T[n1,n2]把每个子带的UDCT系数分成大、小两类来分别统计其状态。

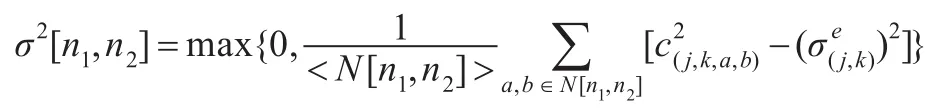
其中,<N[n1,n2]>为以n1,n2为中心的邻域;c(j,k,a,b)为邻域内的UDCT系数。利用式(6)得到子带和其父带的二值图像B[n1,n2],B[n1/2,n2/2]:

式(6)可以得到每个子带和其父带的二值图像即状态分布图,分别统计子带和其父带“大”、“小”状态个数,利用式(7)得到状态转移关系。

其中,number()表示事件发生的次数;m=L,S;按子带内每块是8×8,其父子带是4×4统计,经过多次实验得如图5所示关系。

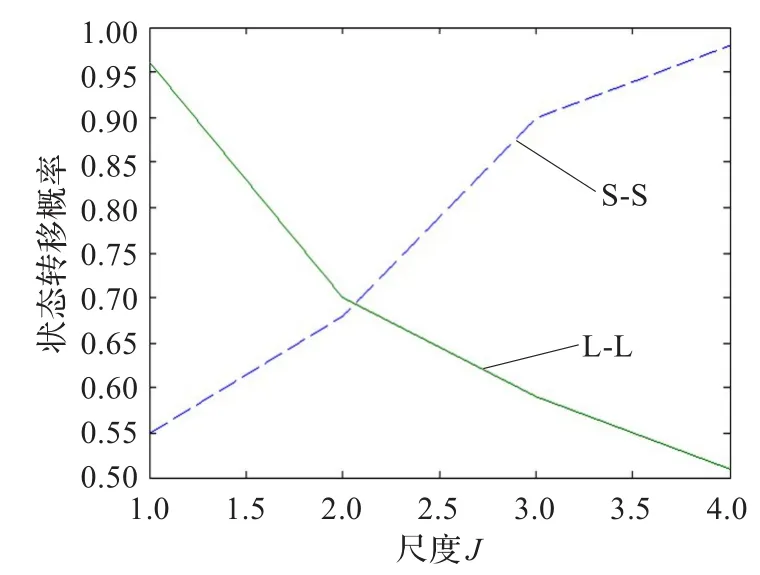
图5 UDCT系数状态转移概率和尺度关系
其中,j为分解层数。用式(8)初始化HMT参数,足以表征状态转移的趋势。UDCT系数随着尺度的增加成指数递减的规律,如图6所示。混合方差的值也反应了UDCT系数的指数衰减性,故可以利用这种规律性初始化方差为:
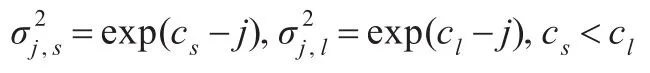

图6 UDCT系数随尺度衰减性
用UDCT系数方差和状态转移的规律对参数估计初始化后用EM算法做参数估计。EM算法过程如下(6通道同时进行):
(2)计算隐状态变量的联合概率密度函数f(c(j,k,n));
(3)更新模型参数θl+1=argmax[lnf(c(j,k,n))|c(j,k,n),θl],用初始化状态转移矩阵减少迭代次数;
(4)l=l+1,若满足收敛条件则停止,否则转(2)。
6 图像去噪
图像去噪问题一般被描述为如式(9)的问题。

y为去噪后的图像UDCT系数;x为含噪图像的UDCT系数;w为噪声的UDCT系数;x为已知的,w为通过随机噪声计算出来的。具体算法步骤为:
(1)对含噪图像进行4层分解,每层的方向分别为6,6,12,12,得到含噪系数x。
(2)对含噪系数进行HMT建模,用EM算法结合提出的改进参数估计方法得到参数集θv,在实验中取cs=2,cl=5,ps1=(0.5,0.5),ui,m=0。
(3)利用式(10)和模型参数θv得到去噪之后的参数θu:

图7 Lena加噪图像不同去噪结果的对比

为Monte-Carlo方法得到的在j尺度,k方向,n位置的噪声方差。
(4)对于给定状态的系数的分布是符合高斯分布的,求解过程可以简化为:

(5)对已求得去噪图像的UDCT系数进行重构就得到去噪之后图像。
通过这种初始化的状态矩阵在保证去噪精度的同时,训练序列的时间减少了2/5,证明该初始化是有意义的。表2所示为改进后的HMT模型算法用到图像序列训练和去噪的时间和其他算法时间的对比。实验图片均采用lena512。当噪声是加性噪声Wiener2函数进行滤波效果较线性滤波器是最好的,算法简单,但不适用于非平稳信号滤波。

表2 UDCT IHMT(优化的)与各种去噪方法时间对比 s
对去噪效果的评价选择峰值信噪比(PSNR)和图像重构以后的结构相似性(SSIM)[12];对lena512进行4层分解,分别用Wiener2、Wavelet HMT[9]、Contourlet HMT[7]、UDCT IHMT四种不同的去噪方法进行对比。表3对应的PSNR的值,表4是对应的结构相似性(SSIM)。
图7是lena512加标准差为40的噪声和各种去噪以后的图像。选择加高斯白噪声的标准差为40,从左到右依次分别为加噪、Wiener2、Wavelet HMT、Contourlet HMT、UDCT IHMT去噪图像。
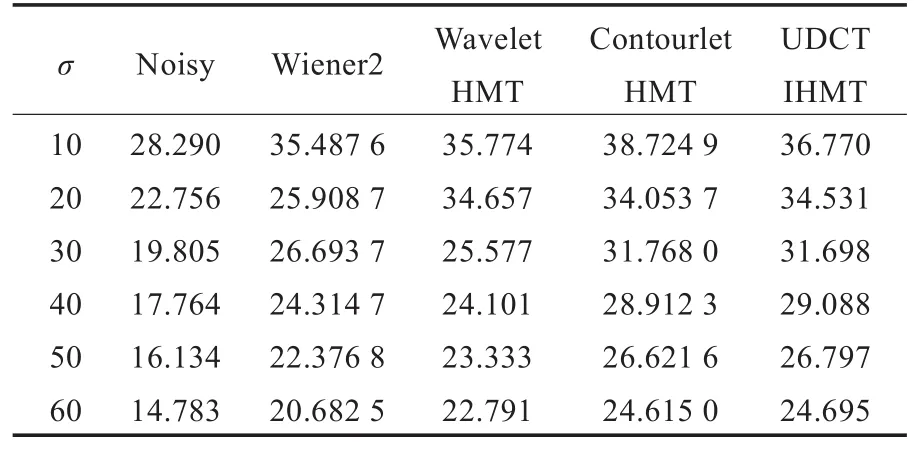
表3 UDCT IHMT与各种去噪方法的PSNR值 dB

表4 UDCT IHMT与各种去噪方法的SSIM对比
7 结论
通过研究UDCT系数X与其父系数PX,邻系数NX,方向系数CX的条件分布,根据互信息量表征各系数之间的联系,用HMT模型来模拟UDCT系数之间的关系,提出初始化方差和状态转移矩阵的方法,保证模型精确性同时节省数据训练时间。通过对比不同的去噪方法证明:虽然算法简单性不如Wiener2,但UDCT的IHMT模型在图像去噪效果方面优于其他方法。
[1]刘仁金,高远飊,郝祥根.文本图像页面分割算法研究[J].中国科学技术大学学报,2010,40(5):500-504.
[2]汪一休.一种交互式图像分割的修正优化算法[J].中国科学技术大学学报,2010,40(2):129-132.
[3]Candes E J,Donoho D L,Ying L.Fast discrete curvelet transform[J].Multiscale Modeling and Simulation,2006,5(3):861-899.
[4]Do M N,Vetterli M.The contourlet transform:an effect directional multi-resolution image representation[J].IEEE Trans on Image Processing,2005,14:2091-2106.
[5]Nguyen T T,Chauris H.Uniform discrete curvelet transform[J]. IEEE Transactions on Signal Processing,2010,58(7):3618-3633.
[6]Crouse M,Nowak R,Baraniuk R.Wavelet-based statistical signal processing using hidden Markov models[J].IEEE Trans on Signal Processing,1998,46:886-902.
[7]Po D D Y,Do M N.Directional multi-scale modeling of images using the contourlet transform[J].IEEE Trans on Image Processing,2006,15:1610-1620.
[8]Moddemeijer R.On estimation of entropy and mutual information of continuous distributions[J].Signal Processing,1989,16(3):233-246.
[9]Liu J,Moulin P.Information-theoretic analysis of inter-scale dependencies between image wavelet coefficients[J].IEEE Trans on Image Processing,2001,10:1647-1658.
[10]Alecu A,Munteanu A,Pizurical A.Analysis of the statistical dependencies in the curvelet domain and applications in image compression[C]//Lecture Notes in Computer Science,2007,4678:1061-1071.
[11]汪西莉,刘芳,焦李成.一种小波域HMT模型参数初始化方法[J].计算机科学,2003,30(1):85-87.
[12]Wang Z,Bovik A C,Sheikh H R,et al.Image quality assessment:from error visibility to structural similarity[J].Image Processing,2004,13:600-612.
YANG Xingming1,CHEN Haiyan1,WANG Gang1,WANG Binbin1,ZHAO Yinping2
1.School of Computer and Information Science,Hefei University of Technology,Hefei 230009,China
2.School of Electrical and Automation Engineering,Hefei University of Technology,Hefei 230009,China
Based on the statistical properties of coefficients of the Uniform Discrete Curvelet Transform(UDCT),and the analysis of correlation metric mutual information about the coefficients,this paper chooses the Hidden Markov Tree to model the coefficients finally and trains the sequence with the EM algorithm.With amount of time consuming,an optimization EM algorithm based on HMT of UDCT coefficients is presented;it further optimizes the algorithm by defining the variance and state transition matrix based on the attenuation of coefficients and continuity between the scales.Experimental results show that,in the use of similarity and Peak Signal to Noise Ratio effect as the measurement of image de-noising,under the same conditions,the algorithm proposed has better real-time and de-noising effect than the Wavelet HMT,Contourlet HMT,UDCT HMT algorithm.
Uniform Discrete Curvelet Transform(UDCT);mutual information;Hidden Markov Tree model(HMT);Expectation-Maximization(EM)algorithm;image denoising
通过对均匀离散曲波变换(Uniform Discrete Curvelet Transform,UDCT)系数的统计特性研究,同时对系数相关性度量指标互信息量的分析,最终选择隐马尔可夫树模型对其系数建模,且用EM算法训练序列;针对训练时间过长问题,通过分析系数的衰减性和尺度间系数延续性,提出一种新的对算法参数初值的方差和状态转移矩阵的优化方法,实验结果证明,在采用峰值信噪比和相似度作为图像去噪效果的度量时,同等条件下文中提出的算法比Wavelet HMT、Contourlet HMT、UDCT HMT算法有较好的实时性和去噪效果。
均匀离散曲波变换;互信息;隐马尔可夫树模型(HMT);最大期望(EM)算法;图像去噪
A
TP751.1
10.3778/j.issn.1002-8331.1112-0463
YANG Xingming,CHEN Haiyan,WANG Gang,et al.Improvement of HMT based on uniform discrete curvelet coefficients and application in image denoising.Computer Engineering and Applications,2013,49(18):195-199.
安徽省2009年度自然科学基金资助(No.090412041)。
杨兴明(1977—),男,博士,副教授,研究方向:小波分析处理,自动控制。E-mail:xmyang@hfut.edu.cn
2011-12-23
2012-02-27
1002-8331(2013)18-0195-05
CNKI出版日期:2012-06-05 http://www.cnki.net/kcms/detail/11.2127.TP.20120605.1519.001.html

