基于改进几何活动轮廓模型的图像分割算法

胡 慧，何聚厚2，，何秀青

1.陕西师范大学 计算机科学学院，西安 710062

2.现代教学技术教育部重点实验室，西安 710062

基于改进几何活动轮廓模型的图像分割算法

胡 慧1，何聚厚2，1，何秀青1

1.陕西师范大学 计算机科学学院，西安 710062

2.现代教学技术教育部重点实验室，西安 710062

1 引言

图像学中准确地进行图像分割和目标轮廓提取对于图像分析、模式识别具有重要意义[1]。传统的图像分割方法大多受噪声和边界轮廓的影响，鲁棒性较差：基于阈值的图像分割对噪声极为敏感且阈值难以选择[2]；基于边缘检测的图像分割不易形成一条封闭的边界轮廓[3]；基于区域的分割时间复杂度较大[4]。由于基于偏微分方程和水平集相结合的分割方法能够闭合、完整地提取目标边缘，故GAC模型近年来广泛应用于图像分割，尤其是用于定位目标边界[5-6]。该模型将二维演化曲线隐含地表达为三维连续函数z=Φ(x，y，t)的零水平集{(x，y)|Φ(x，y，t)=0}。其中，水平集函数Φ(x，y，t)定义为曲线的符号距离函数[7]。该模型存在的主要缺点之一是易出现边界泄漏，尤其是在弱边缘处，故如何减少边界泄露问题已成为该领域的研究热点[8-10]。

针对传统GAC模型的边界泄露问题，不同的研究者从不同角度进行改进。Sumengen等人提出了基于边界流的测地活动轮廓模型[11]，Tsai等人提出了基于图像全局信息的MS模型[12]，Chan等人提出了CV模型[8]，张建伟等提出了高斯混合模型改进的活动轮廓模型[13]。本文主要探讨由常量速度v引起的边界泄露问题。传统GAC模型中，在图像的同质区域和目标边缘演化曲线都具有相同的速度v，当到达目标边界上时，曲线仍然以恒定的速度演化，这样使得先到达弱边界的曲线继续前进，进入到目标的内部，导致边界泄露。针对此缺点，本文提出一个基于GAC模型的变速分割算法，引入与曲线演化位置和边缘角点坐标信息相关的速度改变量Dv对常量速度v进行调节：当演化曲线经过角点时，将角点处速度置零，避免角点丢失，影响边界轮廓提取的准确性；当演化曲线位于弱边缘，将常量速度v减小Dv，防止边界泄露。

2 改进GAC模型

设z=Φ(x，y，t)是水平集函数，GAC模型定义为：

其中，k为曲线的曲率，α＞0为权重系数，v为常量速度，(v+αk)相当于曲线沿法线方向的演化速度。g(|∇I|)为“边缘检测函数”，该函数取关于图像梯度的一个严格递减非负函数，且函数满足“在梯度较大的地方其函数值理想状态下为零，在平滑区域其函数值为较大的正值”的性质。边缘检测函数定义为式（2）：

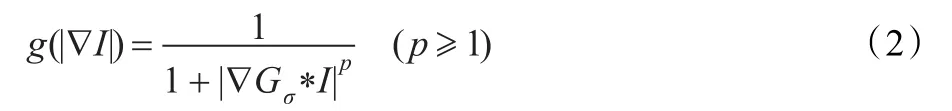
其中，Gσ为标准差为σ的Gaussian滤波器，∇为梯度算子，∇Gσ*I为图像I(x，y)经过Gaussian滤波后的梯度。

根据边缘检测函数g的表达式，停止速度在目标边界处并不为0，而且在弱边界上停止速度可能较大，因此，当演化曲线先到达目标弱边界或角点时，很容易继续演化进入目标内部，产生边界泄露。针对此问题，研究者对传统GAC模型式（1）进行了改进，Yezzi提出了如式（3）所示的测地活动轮廓模型（geodesic active contours）[14]：

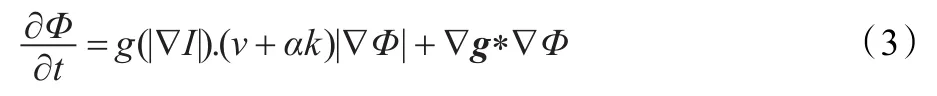
在原模型的基础上增加了∇g*∇Φ，这一项是向量∇g在水平集法线方向上的投影，吸引曲线向目标边界演化。该模型对于复杂边界和弱边界仍然有可能出现边界泄露，且曲线演化速度是常量。

针对上述缺点，本文提出的变速分割算法首先提取出目标边缘角点集Cοrners：

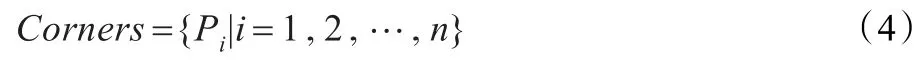
其中n为目标边缘的角点个数。对于每一个角点Pi，有：

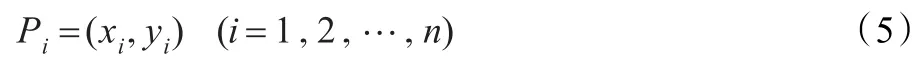
若两角点Pi、Pj(i≠j)之间为弱边界，则当曲线演化到xi＜x＜xj，yi＜y＜yj时，改变常量演化速度v：v′=v-Dv。

将式（1）中常量速度v替换为式（6）：

则改进GAC模型定义为：

改进GAC模型中以变化的速度v′代替传统GAC模型中的常量速度v，目的是使演化曲线在图像的同质区域以较大的常量速度v演化，减少演化时间；在曲线演化到目标的弱边界时速度趋近于零，在角点处时速度为零，减少因常量速度v引起的边界泄漏，提高目标轮廓提取的准确性。

3 基于改进GAC模型图像分割过程描述

3.1 算法模块图及概述

该分割算法模块图如图1所示。

图1 算法模块图

该分割算法主要针对传统GAC模型中的常量速度v进行改进，分割过程分为四大模块：

（1）图像预处理：将原图像转化为灰度图，并进行尺寸归一化及高斯去噪处理。

（2）角点提取：首先应用Canndy算子获得边缘图；再提取轮廓曲线并根据公式计算曲率，选取局部曲率极大值点作为候选角点，将圆角点剔除，得到正确的角点集；选取位于轮廓边缘的角点并在灰度图上标记坐标。角点提取过程如图2所示。

图2 角点提取过程

（3）水平集初始化及更新：根据公式计算边缘函数g并初始化水平集函数，再结合图像边缘梯度信息以速度v迭代更新水平集。水平集更新过程如图3所示。

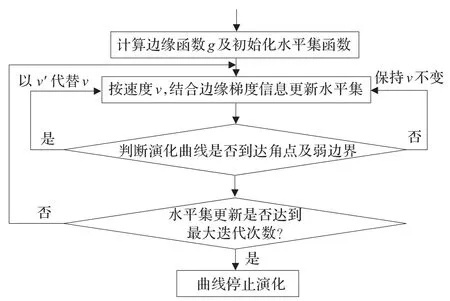
图3 水平集更新过程

水平集迭代更新的过程为：根据变分水平集方法的能量泛函E(u)得到梯度下降流表达式，并获得其显示方案；再根据角点坐标信息判断演化曲线是否抵达角点及弱边缘，若角点已在演化曲线上，将角点处速度置零；若曲线已演化到弱边缘处，将速度v替换为v-Dv，否则，常量速度v保持不变；最后按照预先设置的时间步长更新水平集，直到达到最大迭代次数，更新过程停止。

（4）分割结果输出：曲线停止演化后，Φ的零水平集{(x，y)|Φ(x，y，t)=0}即为最终的分割结果。

3.2 算法步骤

步骤1图像预处理：设I(x，y)是待分割图像，将I(x，y)转化为灰度图像I′(x，y)，归一化图像大小并做去噪处理。

步骤2角点提取及坐标信息记录。

步骤2.1对灰度图I′(x，y)应用Canndy算子，获得二值边缘图。

步骤2.2从二值边缘图提取轮廓曲线Curve，填充轮廓曲线中的断点。

步骤2.3根据式（12）计算曲线上任意一点处的曲率：

将曲线Curve写成如下以弧长s为参数的函数形式：

设Curve(s，σ)为曲线Curve在尺度σ下的参数形式，即

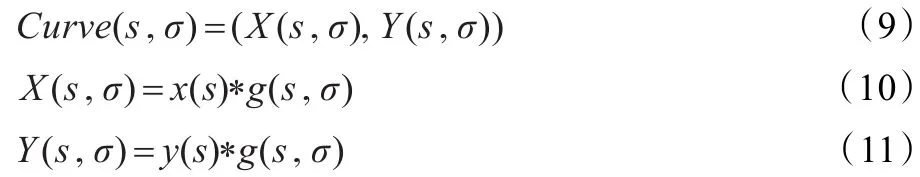
其中，*是卷积算子，g(s，σ)是尺度σ下的高斯函数。

则轮廓曲线Curve(s，σ)的曲率公式为：

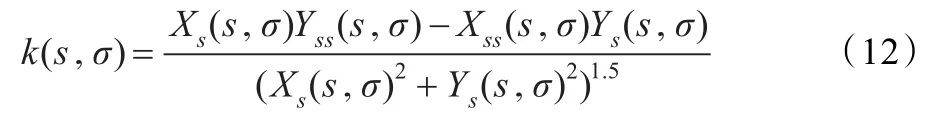
其中：

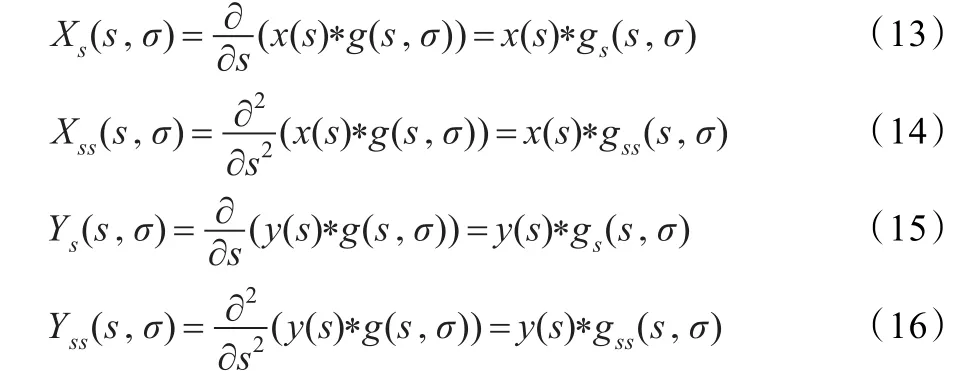
在式（13）～式（16）中，gs(s,σ)，gss(s,σ)分别表示g(s,σ)关于s的一阶和二阶导数。

步骤2.4将局部曲率最大点作为候选角点，剔除圆角点，得到正确的角点集合Cοrners。

步骤2.5返回轮廓边缘角点坐标并在灰度图中标记出角点位置(xi，yi)。

步骤3初始化时间步长Dt和最大迭代次数nmax。

步骤4计算目标区域图像的梯度模值和边缘函数g及初始化水平集u。

根据公式（2）计算边缘检测函数g，按照公式（17）初始化水平集u（c为符号距离）：

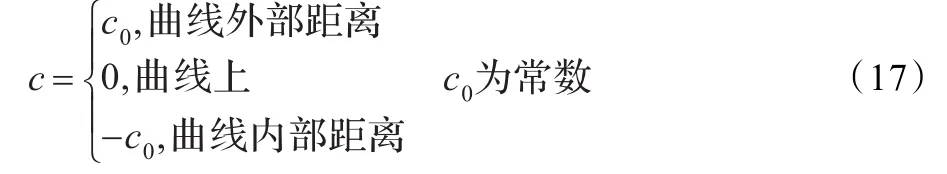
步骤5更新水平集u：根据变分水平集方法的能量泛函E(u)得到梯度下降流为：

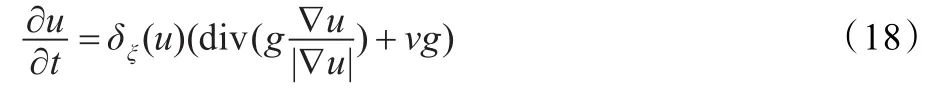
采用“半点离散化”计算div，即

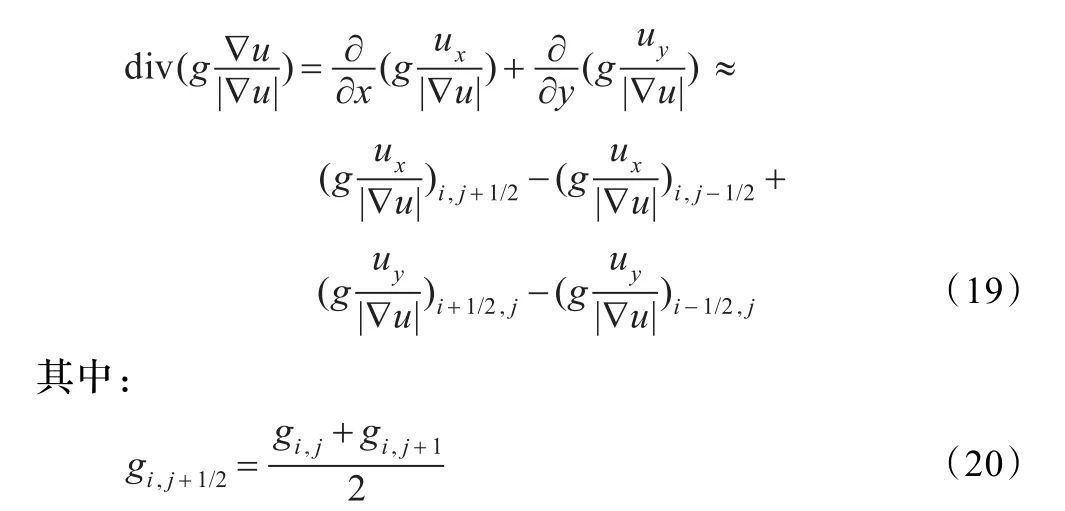
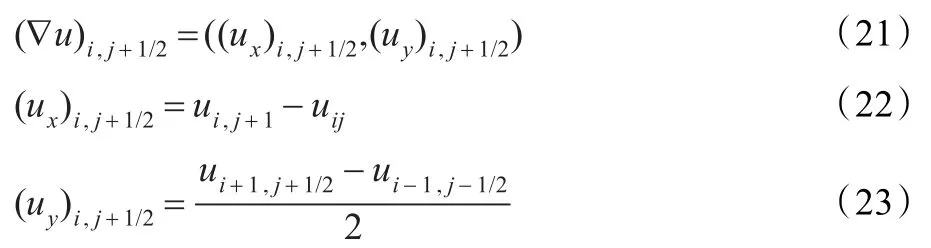
则公式（18）的显示方案为：

步骤6根据角点坐标和演化曲线位置，调整曲线速度v：若角点已在演化曲线上，将角点处的演化速度置零：v′=0；若曲线演化到弱边界处，改变常量速度v为v′=v-Dv。反之，保持常量速度v不变。

步骤7曲线演化终止条件的判断：当迭代次数n=nmax时，曲线停止演化，获得最终的分割结果。

4 实验及结果分析

为验证本文提出方法的有效性，实验中选取了两幅角点明显且具有弱边缘的图像，将图像转化为灰度图，尺寸归一化为256×256，并做去噪处理。分别使用传统GAC模型与改进GAC模型做对比实验，从分割性能和时间性能两个方面比较实验结果。

实验平台操作系统为Windows7，编程环境为Matlab7.0。实验参数设置为：时间步长Dt=5；根据图像设置最大迭代次数nmax，选取分割结果最准确的nmax作为最终迭代次数；初始常量速度分别设置为0.15、0.2、0.3、0.4。

将两幅彩图转化为灰度图后，如表1所示。

表1 灰度图

实验1第一幅灰度图像的分割实验：对图像1进行角点提取，边缘角点坐标Cοrners1为：

采用传统GAC模型与本文方法分别在不同初始化速度下对图像1进行分割，分割结果如表2所示。

结果分析：实验1中分别取常量速度v=0.15、0.20、0.30使用传统GAC模型与改进GAC模型对图像1进行分割。由表2可知，随着初始速度v的增大，传统GAC模型的边界泄露现象越来越明显，尤其是在弱边界处。采用本文方法，先提取灰度图的角点集Cοrners1，当曲线演化到角点和弱边界处，分别改变初始速度的值，防止活动曲线越过弱边界。表2第3列分割结果显示，改进算法有效地减少了边界泄露现象，分割结果比较准确。

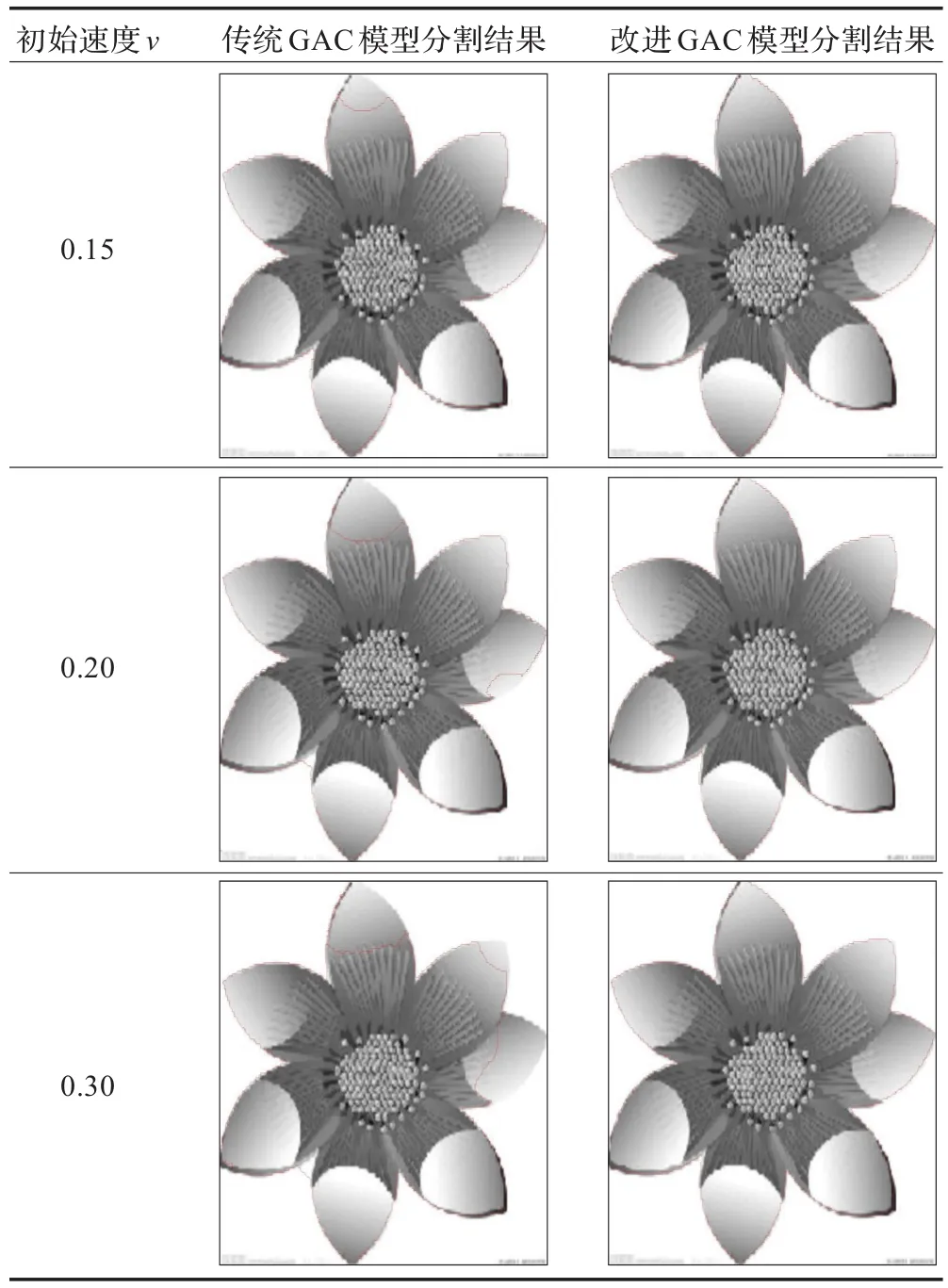
表2 不同速度下传统GAC模型和改进GAC模型图像1分割结果

实验2第二幅灰度图像的分割实验：对图像2进行角点提取，边缘角点坐标Cοrners2为：

结果分析：实验2中分别取常量速度v=0.2、0.3、0.4使用传统GAC模型与改进GAC模型对图像2进行分割。由表3分割结果对比可知，针对目标边缘及角点处与背景对比度较小的图像，传统GAC模型的分割结果显示，在不同初始速度下出现了不同程度的边界泄露及角点丢失现象，提取的目标轮廓极不准确；采用本文算法通过改变演化曲线到达角点及弱边界处的速度，分割效果较传统GAC模型有较大的改进。

使用传统GAC模型与改进GAC模型分别对图像1和图像2进行分割的时间对比如表4和表5所示。

结果分析：在改进GAC模型中，采用了变分水平集方法，故无需对演化曲线进行重新初始化，由表4和表5数据可知，改进GAC模型较传统GAC模型分割时间更短，且结合本文对曲线演化速度的改进，分割结果也更加准确。

表3 不同速度下传统GAC模型和改进GAC模型图像2分割结果

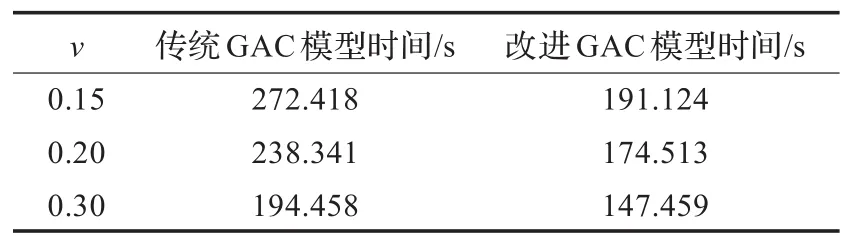
表4 不同速度下传统GAC模型和改进GAC模型对图像1的分割时间

表5 不同速度下传统GAC模型和改进GAC模型对图像2的分割时间

5 结束语

本文提出了一个基于改进GAC模型的变速图像分割算法，该算法用结合边缘角点坐标信息和演化曲线位置的速度v′代替传统GAC模型中的常量演化速度v，对角点处及弱边界的演化速度做不同调整。实验结果表明：相对传统的GAC模型，本文算法能够在更短的时间内得到更加准确的分割结果，在一定程度上减少了边界泄露，尤其是在弱边缘及角点处。但本文的分割算法仍然要求初始曲线包围目标物体，因此，下一步研究工作将是对任意位置初始曲线的分割算法的探讨。

[1]陈波，赖剑煌.基于水平集曲线演化的目标轮廓提取[J].计算机科学，2006，33（8）：227-235.

[2]石振刚，高立群.一种基于模糊连通度的图像闭值分割算法[J].计算机工程，2009，35（8）：241-243.

[3]Canny J.A computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1986，8（6）：679-698.

[4]Adams R，Bischof L.Seeded region growing[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1994，16（6）：641-647.

[5]Lee S H，Seo J K.Level set-based bimodal segmentation with stationary global minimum[J].IEEE Trans on Image Processing，2006，15（9）：2843-2852.

[6]He Chuanjiang，Tang Liming.Anisotropic diffusion of halting speed fieldsin geometric active contourmodel[J].Journal of Software，2007，18（3）：600-607.

[7]唐利明.基于GAC模型的自适应图像分割算法[J].小型微型计算机系统，2010，131（6）：1223-1225.

[8]Chan T F，Vese L A.Active contours without edges[J].IEEE Trans on Image Processing，2001，10（2）：266-277.

[9]Deng J W，Tsui H T.A fast level method for segmentation of low contrast noisy biomedical images[J].Pattern Recognition Letters，2002，23（1）：161-169.

[10]邱明，张二虎，张志刚.基于改进的GVF模型的CT图像分割方法[J].小型微型计算机系统，2006，27（1）：155-157.

[11]Sumengen B，Manjunath B S，Kenney C.Image segmentation using curve evolution[C]//Proc of the Conf on Record of the 35th Asilomar Conference on Signals，Systems&Computers，2001：1141-1145.

[12]Tsai A，Yezzi A，Willsky A S.Curve evolution implementation of the Mumford-Shah functional for image segmentation，denoising，interpolation，and magnification[J].IEEE Trans on Image Processing，2001，10（8）：1169-1186.

[13]张建伟，夏德深.高斯混合模型改进的活动轮廓模型MRI分割[J].计算机辅助设计与图形学学报，2005，17（12）：2647-2653.

[14]Yezzi A，Kichenassamy S，Kumar A，et al.A geometric snake model for segmentation of medical imagery[J].IEEE Trans on Medical Imaging，1997，16（2）：199-209.

HU Hui1,HE Juhou2，1,HE Xiuqing1

1.School of Computer Science,Shaanxi Normal University,Xi’an 710062,China
2.Key Laboratory of Modern Teaching Technology,Ministry of Education,Xi’an 710062,China

A variable speed image segmentation algorithm based on enhanced Geometric Active Contour（GAC）model is proposed in order to solve the problem that traditional GAC model usually leaks boundary.The algorithm combines image edge gradient information and coordinate information of corners.In the algorithm,the constant speed of evolution curve on the corners and weak boundary is changed to avoid active contour curve continue evolution into the target boundary,causing boundary leakage and corner loss,influencing the accuracy of target contour extraction.The experimental results show that the proposed algorithm can make the evolution curve stop at the edge of target more accurately and reach an obvious effect in terms of boundary leaking, in comparison with traditional GAC model.

geometric active contour model;level set;image segmentation;corner extraction;boundary leaking

针对传统几何活动轮廓（GAC）模型易出现边界泄露的缺陷，提出一个基于改进GAC模型的图像变速分割算法。该算法结合了图像边缘梯度信息和边缘角点坐标信息，通过改变演化曲线在角点及弱边界处的常量速度，避免活动轮廓曲线继续演化进入目标边界内，造成边界泄露和角点丢失现象，影响目标轮廓提取的准确性。实验结果表明：该算法可使演化曲线更加准确地停在目标边缘，并且在一定程度上减少了边界泄露问题。

几何活动轮廓模型；水平集；图像分割；角点提取；边界泄漏

A

TP391

10.3778/j.issn.1002-8331.1303-0097

HU Hui,HE Juhou,HE Xiuqing.Image segmentation algorithm based on enhanced geometric active contour model. Computer Engineering and Applications,2013,49（18）：149-152.

中央高校基本科研业务费专项资金资助（No.GK201002028，No.GK201101001）；陕西师范大学研究生创新基金资助（No.2013CXS042）。

胡慧（1987—），通讯作者，女，硕士研究生，主要研究方向：计算机支持的协作学习；何聚厚（1972—），男，博士，副教授，主要研究方向：计算机网络安全，技术增强学习；何秀青（1972—），女，博士，讲师，主要研究方向：技术增强学习。E-mail：huihu586@126.com

2013-03-08

2013-05-07

1002-8331（2013）18-0149-04