云计算环境下的PSO可信资源调度

丁燕艳，潘 郁，程仕伟

南京工业大学 经济与管理学院，南京 211816

云计算环境下的PSO可信资源调度

丁燕艳，潘 郁，程仕伟

南京工业大学 经济与管理学院，南京 211816

1 引言

云计算是并行计算（Parallel Computing）、分布式计算（Distributed Computing）和网格计算（Grid Computing）的发展[1]，是这些计算机科学概念的商业实现。云计算能提供动态资源池、虚拟化和高可用性的下一代计算平台的核心技术。它将计算任务分布在大量计算机构成的资源池上，使各种应用系统能够根据需要获取计算力、存储空间和各种软件服务，并按照使用付费。不同于网格计算，云计算具有更广泛含义的计算平台，能够支持非网格的应用。且云计算使用的是集中的资源，而网格计算实际上是收集分散的资源，在资源的占用上，区别于网格的独占式的资源分配模式，云中的资源将被所有的用户同时共享。考虑云计算本身的特性及与网格计算的差异性，现有的大量针对网格计算的资源分配和调度的算法无法直接移植到云计算环境下。

现有为数不多的关于云计算环境下资源调度的文献中，文献[2]提出的具有双适应度的遗传算法（DFGA）能有效地解决云计算环境下资源的分配问题，文献[3]提出的基于蚁群优化（Ant Colony Optimization）的计算资源分配算法通过在Gridsim环境下的仿真分析和比较，亦证明其能在满足云计算环境要求的前提下有效地调度资源。文献[4]运用离散粒子群算法对云计算环境下的负载均衡问题进行研究，根据云计算环境下资源需求动态变化建立相应的资源-任务分配模型，提高了资源利用率和云计算资源的负载均衡。但这些模型中鲜有考虑到任务间的输入输出关系、执行顺序，策略中也很少考虑动态节点资源的可信性问题。实际上，任务的串并联结构在实际的操作中是非常现实的，且动态提供的资源的可信性无论对云计算基础运营商，还是对服务运营商，都是非常关键的因素。因此，结合任务间的结构关系、云计算环境下节点本身性能低、易失效的特点和资源请求表现出的很强的波动性，为保证动态提供的资源的可信性，又不影响资源的使用效率，本文提出了一种基于任务结构的更加可信的资源动态调度策略。

本文首先介绍云计算环境下基于任务间串并联结构和输入输出关系的动态资源分配模型，然后在考虑了节点资源可信性的基础上，提出了云计算环境下基于可信性的动态资源分配模型，最后通过Matlab进行仿真实验，实验结果验证了算法的可行性，以及与其他没有考虑节点可信性算法相比时解的质量的优越性。

2 问题描述

资源调度具体包括三个子问题：映射任务；给出任务调度顺序；给出资源上任务的执行顺序。本文采用无环有向图 Directed Acyclic Graph（DAG）来映射任务[5]，由G=(V，E)表示，如图1所示。其中，每个节点V代表不同的任务T，T={T1，T2，…，Tk}表示任务T的集合。边E代表了任务间的关联度，即任务间是否存在输入输出关系。若(Tj，Tk)∈E，则用fik表示Tj产生数据并输入Tk。S={S1，S2，…，Sj}表示存储资源节点的集合，PC={PC1，PC2，…，PCj}代表计算资源节点的集合。

假设存在5个任务T={T1，T2，…，T5}，任务间的作业先后顺序如图1中左图所示。同时，假设有3个资源节点可供调度如图1中右图所示。则资源调度的目标就是在不超过截止期的前提下，充分合理地利用各种可用资源，最大限度地减少服务的开销，使服务价值最大化。

由于云计算服务中心的大量低性能、廉价计算机集群中，节点的失效对于调度策略的性能具有较大的影响，因此在问题模型中引入了可信度的概念，即在节点分配的过程中，结合节点失效的特征，选择可靠性较高的节点来运行作业，提高调度性能。

研究表明，节点资源的失效表现出很强的时间局部规律性，即在运行周期中不同的时间段内表现出不同的特征，可看作是一个随机过程，这个随机过程符合参数β为1的韦伯分布[6]，记为W(α，β)。其中α称为尺度参数，β称为形状参数，其概率密度和分布函数分别为：

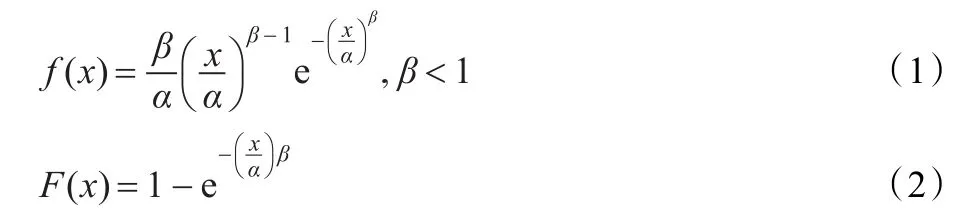
当β=1时，W(α，1)就是参数为α的指数分布。

韦伯分布是可靠性中广泛使用的连续型分布，它可以用来描述疲劳失效，真空管失效和轴承失效等寿命分布。结合式（1）、（2）易得单个节点的失效函数为：

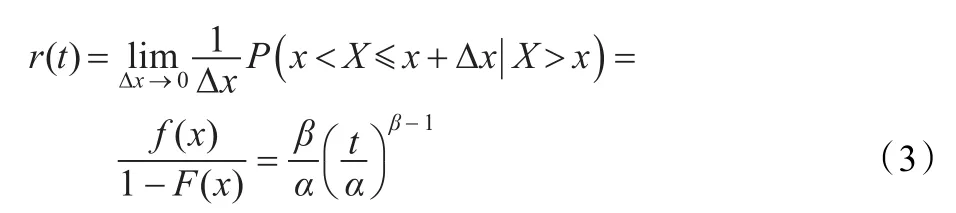
易见，当β＞1时，r(t)是递增的；当β＜1时，是递减的；当

根据节点失效的特征，可以将节点失效分为三类：永久失效、间歇性失效和瞬间失效。如果某节点发生永久性失，则使用另一个新的节点代替该节点的功能，对于用户而言相当于发生了一次节点重启事件。而间歇失效和瞬间失效则可以通过节点的重启来修复。因此，可以将计算机集群中节点的失效看作节点的重启[7]。当节点系统运行到一定的时间门限值tmax，即节点的恢复时间，对此节点进行重启，节点的可靠性提高。

文献[8]也指出了云计算环境下，节点无计划重启的失效概率有随运行时间先下降后上升的趋势。这说明节点在刚刚启动时可靠性较低，容易出故障，之后在正常运行时间超过一定值后，故障率又开始上升，节点变得越来越不可靠。

由此，根据资源节点失效的特性，得出节点正常运行的可信度函数为：

其中t是节点运行时间，根据云环境下节点运行的规律，在节点刚启动时α＜1，其可信性随着时间的增加而增加；当节点运行到一个稳定的时间门限tmid后，节点的可信性随着时间的增加而降低；当节点运行到时间门限值tmax后，节点进行重启，α＜1。

3 建立模型

本文以服务价值最大化为目标，其中总成本Ct由两个部分组成，一是计算资源的服务使用费Ca，另一部分为任务间数据传输引起的传输费用Cb，此项费用当且仅当任务节点间存在输入输出关系时产生。其中：

表示计算资源节点PCj上所有任务T的计算费用，wkj表示将任务Tk分配到节点PCj上的费用。

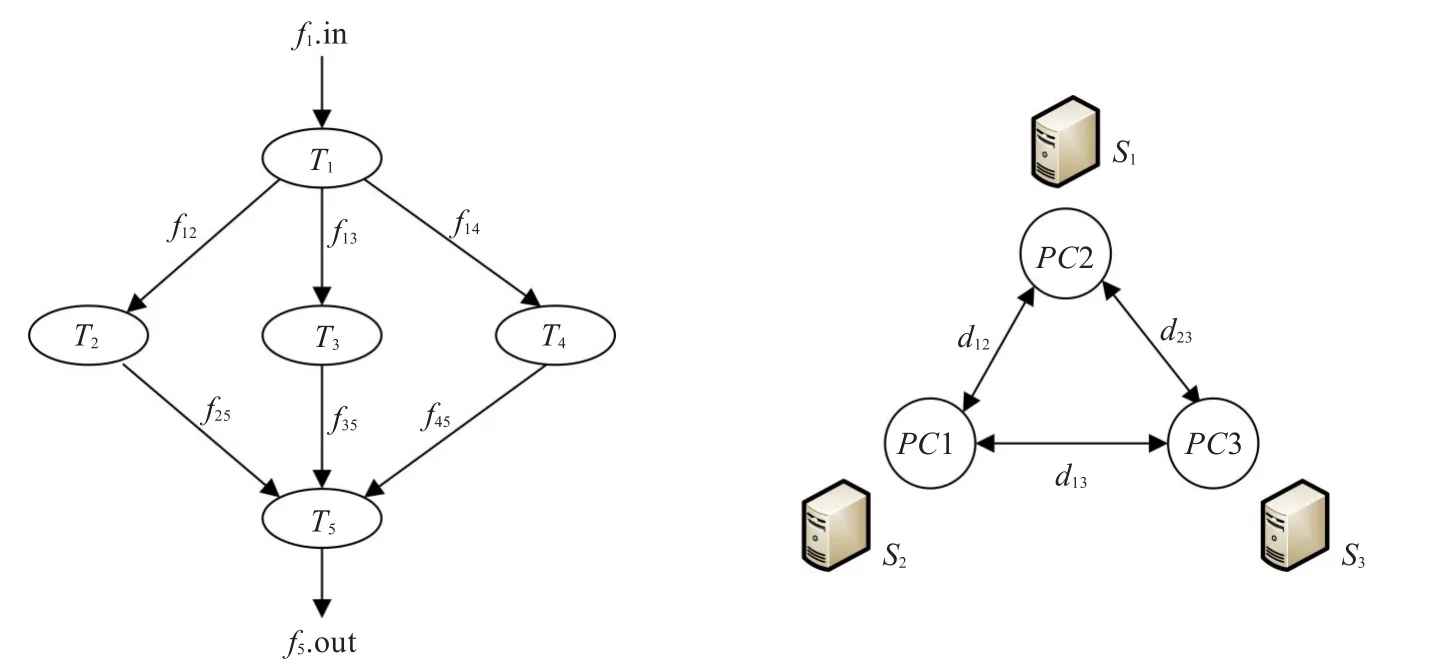
图1 任务映射图

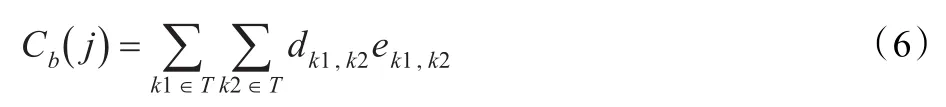
表示任务k1输出传输给任务k2产生的费用，其中k1≠k2，ek1，k2为DAG中边的权重，代表任务间的数据传输量，dk1，k2为单位数据传输费用。当且仅当ek1，k2＞0时，存在Cb(j)。

上文已指出，在资源调度的过程中，节点的失效将会大大地影响调度的效率和性能。因此结合资源节点的可信性，给出了节点的可信调度策略。定义目标函数为：

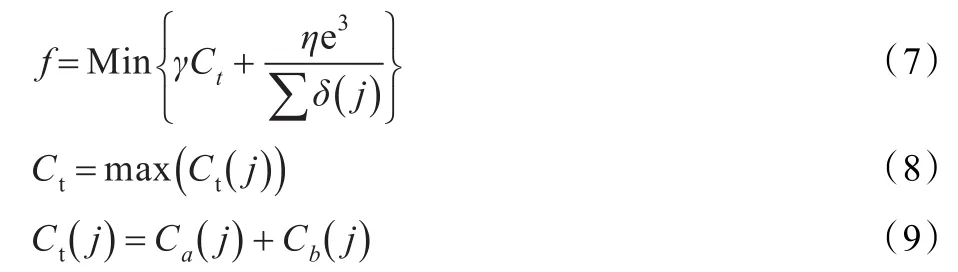
其中式（8）确保了在资源分配初期，所有的任务尽可能均匀地分派到各个节点上。式（9）为节点PCj的总费用。γ，η分别为费用和可信度的权重系数，0＜γ，η＜1，且γ+η=1。

4 算法求解

粒子群算法（Particle Swarm Optimization，PSO）最早是Kennedy和Eberhart于1995年提出的，该算法是通过群体粒子间的合作与竞争产生集群智能指导的并行搜索算法[9-10]，用来解决传统搜索方法解决不了的目标函数超曲面复杂和非线性问题。

该算法中每个优化问题的解都被抽象成搜索空间中的一个没有大小和质量的“粒子”。所有的粒子都有自己在空间中的位置和一个适应值，每个粒子还有一个速度决定它们飞翔的方向，然后粒子们就追随当前的最优粒子在解空间中搜索。在搜索过程中，粒子通过跟踪两个“极值”来更新自己。第一个就是初始到当前迭代历史中搜索产生的粒子本身的最优解，即个体极值Pbest，另一个极值为整个种群中当前的最优解，即全局极值Gbest。

在本文，因为资源调度属NP完全问题，因此用PSO算法中的离散粒子群算法求解。具体地，定义第t次迭代时第i个粒子在m维空间的位置为其中，表示任务T1第t次迭代时选择的资源

节点为PCi，k为总的任务数量。将目标函数值最小作为评价标准，即适应度函数为：

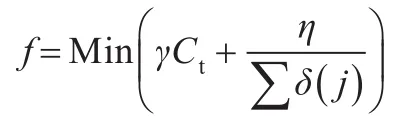
其中，i=(1，2，…，n)，w为惯性因子，Rand1()和Rand2()均是在（0，1）区间上独立同分布的均匀分布随机数。c1和c2为学习因子。以图1为例，随机产生一个初始解如图2所示，将其映射到PSO算法中，其解的形式为[1，2，1，3，2]。

图2 解的构造

5 算法实现

鉴于本问题模型的数学结构，设计粒子群优化算法伪代码如下。

（1）计算各个任务在所有节点上的服务使用费用，建立服务使用费列表

（2）建立各个节点数据传输费用列表

（3）建立任务间数据传输量表

（4）建立节点可信度列表

（5）建立任务执行顺序序表

（6）初始化PSO算法中相关参数

Repeat

扫描任务执行顺序序表，建立ready task表

%ready task存放符合任务先后执行顺序表的合法任务，且当下可以马上为其调度资源的任务。

for所有的 ready tasks{Ti}{Ti}∈Tdo

根据PSO算法将资源{PCj}分配到任务{Ti}上

end for

%派遣所有ready task的任务

等待系统投票执行

更新ready tasks列表

%为被阻塞的后续任务分配资源，将其加入ready task，并将已完成的任务从中ready task的任务集合中删除。

根据当前任务间的负载情况更新数据传输列表

计算PSO相关值

until所有的任务都调度完毕

6 算法仿真与结果分析

本文采用Amazon Web Service中的Elastic Compute Cloud（EC2）和Cloud Front服务的相关费用作为云计算服务中计算和传输服务的费用[11]。具体任务结构如图1所示。其中，为了更加符合商务活动、科学活动全球化趋势，以及凸显数据传输代价的差异性，本文使任务在不同云计算服务中心间进行数据传输，且假设终端所在地无服务中心。

为此设PC1、PC2、PC3分别为Amazon位于United States East的Virginia、European Union的Ireland和Asia Pacific的Singapore。不同区域的服务费用如下：矩阵AS、BI、BO分别为任务计算服务费用、单位（TB）数据输入和输出费用（数据量不同费用不同），DC表示不同任务输入输出时数据量的变化，费用单位为美元$，数据量单位为TB，具体如下：

由于云计算的一个局部可以看作一个特殊的网格环境，所以本文用Cloudsim来模拟一个云计算的局部环境，并采用Matlab7.1进行仿真分析。其中，主要参数设置如下：b=5，γ=0.45，η=0.55，c1=2，c2=2。该算例选取粒子群体规模为25，迭代次数为20。机器的可靠性概率初始分布和初始解均由计算机随机生成。执行结果如图3所示，图中可以看出，算法收敛于最优解9.897 5，证明了算法的可行性。

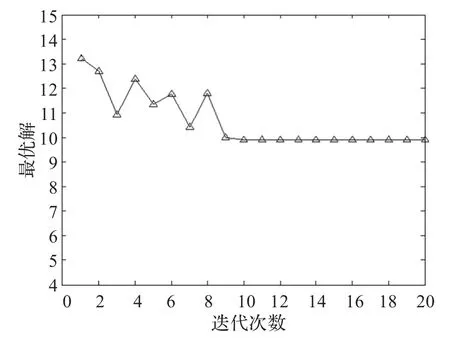
图3 算法收敛情况

针对上述的算例，本文对b的取值进行了变化使得最大数据传输量超越了10 TB、40 TB、100 TB、150 TB四个临界值，计算对应任务的资源调度分布情况，结果如图4所示。图4表明在该算法下，所有的任务都被均衡地分布在各个资源上，实现了资源最大化利用。从该图中也可以看出，当数据量较小时，任务以较大概率分配到计算费用较低廉的服务节点上，但随着数据量的上升，任务被均匀地分布到各个节点。此结果表明在数据量较小的情况下可优先考虑可信度高且费用开销较低的节点，数据量较大的时候可以均匀地分配任务提高完成效率。

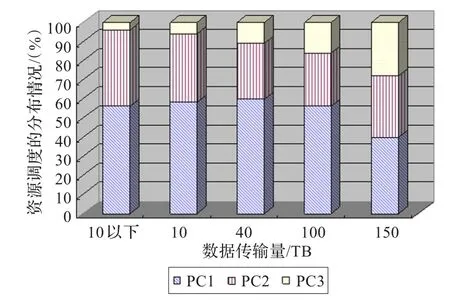
图4 负载分布情况

任务的成功分配率即云用户的任务能够在规定的期限di内完成的完成率，定义任务的成功分配率[12]公式如下：

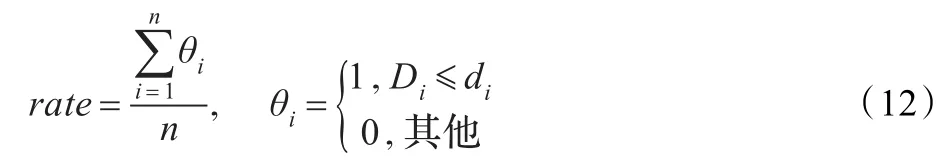
其中，Di表示任务Ti的完成时间。

为了更好地验证本文提出的算法的有效性，在上述的仿真环境和参数设置下，对算例中的规模进行扩展后，将文献[2]中提出的算法以及不考虑节点可信性的粒子群算法，与本文所提出的考虑节点资源可信性的分配算法进行失效测试比较，即比较各个算法的任务的成功分配率。

在模拟的云计算局部环境下，设置了模拟任务的任务截止期，将用户并发数量从50增加到350，记录其任务的成功完成情况，图5为50次实验的成功分配率的平均值。从图5可看出，基于可信性的资源分配策略相对于没有考虑可信性的资源分配策略有更高的任务成功执行率。

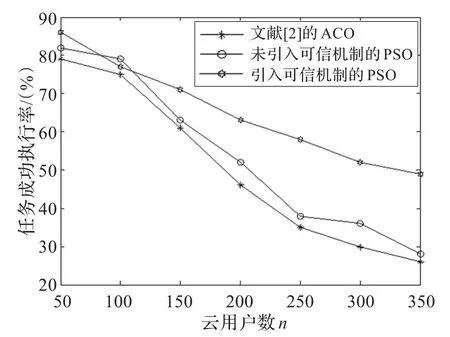
图5 任务成功分配率

7 结论

云计算环境下，面对海量信息的存储、计算和传输，其提供的诸如Saas，Paas等服务却比网格对基础设施的要求更高，所以一个好的资源调度算法尤为重要。本文提出的基于可信性的且有作业串并联结构的云计算资源分配模型能较好地模拟现实作业，且算例测试中采用了Amazon Web Service的真实数据，结合粒子群算法求解，结果能较好地说明算法的可行性，且该模型的执行性能明显优于没有考虑节点可信性的资源分配模型，能更可靠更高效地完成云计算环境下的计算资源搜索与分配工作。

[1]Marston S，Li Z，Bandyopadhyay S.Cloud computing—the business perspective[J].Decision Support Systems，2011，51（1）：176-189.

[2]华夏渝，郑骏，胡文心.基于云计算环境的蚁群优化计算资源分配算法[J].华东师范大学学报：自然科学版，2010（1）：127-134.

[3]李建锋，彭舰.云计算环境下基于改进遗传算法的任务调度算法[J].计算机应用，2011，31（1）：184-186.

[4]冯小靖，潘郁.云计算环境下的DPSO资源负载均衡算法[J].计算机工程与应用，2013，49（6）：105-108.

[5]Pandey S，Wu Linlin，Guru S M，et al.A Particle Swarm Optimization（PSO）-based heuristic for scheduling workflow applications in cloud computing environments[C]//24th IEEE International Conference on Advanced Information Networking and Applications，Australia，2010，1（1）：400-407.

[6]曹晋华.可靠性数学引论[M].北京：高等教育出版社，2006：15-16.

[7]武林平，孟丹.LUNF——基于节点失效特征的机群作业调度策略[J].计算机研究与发展，2005（6）：1000-1005.

[8]Sahoo R K，Sivasubramaniam A，Squillante M S.Failure data analysis of a large-scale heterogeneous server environment[C]//Proceedings of the DSN2004，Florence，Italy，2004：772-784.

[9]陈森发.复杂系统建模理论与方法[M].南京：东南大学出版社，2005.

[10]Zhu Hanhong，Wang Yi，Wang Kesheng，et al.Particle Swarm Optimization（PSO）for the constrained portfolio optimization problem[J].Expert Systems with Applications，2011，38（8）：10161-10169.

[11]Amazon products[EB/OL].（2011-04-29）.http：//aws.amazon. com/.

[12]Chang Guiran，Wang Chuan，Xiong Yu，et al.Efficient Nash equilibrium based cloud resource allocation by using a continuous double auction[C]//2010 InternationalConference on Computer Design and Applications，2010：194-199.

[13]刘鹏.云计算[M].北京：电子工业出版社，2010：16-56.

DING Yanyan,PAN Yu,CHENG Shiwei

School of Economics and Management,Nanjing University of Technology,Nanjing 211816,China

The resource scheduling problem in cloud computing environment is discussed.According to the characteristics of the cloud computing environment,the tasks structure and the node failure,a mathematical resource scheduling model is established.The discrete particle swarm algorithm is used to solve the problem.The simulation test example is created according to the facts of the cloud computing service operation and the verification shows that the model is rational and the algorithm is feasible and effective.

cloud computing;resource scheduling;particle swarm algorithm;creditability;Weibull distribution

对云计算环境下的资源调度问题进行了研究。针对云计算环境下资源调度的特点，结合节点失效以及任务间的网状结构特点，建立资源调度问题数学模型，运用离散粒子群算法求解该问题。针对模型特点结合云计算服务运营实情，设计算例进行仿真测试。验证表明了所建立模型的合理性及该算法求解的可行性和有效性。

云计算；资源调度；粒子群算法；可信度；韦伯分布

A

TP393

10.3778/j.issn.1002-8331.1112-0284

DING Yanyan,PAN Yu,CHENG Shiwei.Creditable resource scheduling based on particle swarm algorithm in cloud computing.Computer Engineering and Applications,2013,49（18）：78-81.

南京市科技计划项目（No.201007006）。

丁燕艳（1987—），女，硕士，研究方向：管理决策与人工智能；潘郁（1955—），男，教授，研究方向：计算管理与商务智能；程仕伟（1987—），男，硕士，研究方向：计算管理系统与人工智能。E-mail：dingyanyan77@163.com

2011-12-14

2012-04-09

1002-8331（2013）18-0078-04

CNKI出版日期：2012-05-21 http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1142.056.html