融合邻域粗糙集与粒子群优化的网络入侵检测
赵晖
陕西理工学院 数学与计算机科学学院,陕西 汉中 723000
融合邻域粗糙集与粒子群优化的网络入侵检测
赵晖
陕西理工学院 数学与计算机科学学院,陕西 汉中 723000
1 引言
入侵检测是一种通过收集和分析被保护系统信息来发现入侵的主动网络安全技术,主要功能是对网络和计算机系统进行实时监控,发现和识别系统中的入侵行为,发出入侵警报。入侵检测一般被视为系统状态是“正常”或“异常”的二分类问题。
入侵检测领域中所获得的数据具有非线性及高维特点,且数据往往并不服从某种已知分布,这就使得传统统计学的方法难以进行有效的检测,神经网络、贝叶斯网络、支持向量机以及K邻近等机器学习方法被用于入侵检测领域,其中支持向量机(Support Vector Machine,SVM)[1-4]是建立在统计学习理论基础上,以结构风险最小化为准则的机器学习方法,具有结构简单、全局优化、训练时间短、泛化性能好等优点,较好地解决了高维、非线性、小样本等问题。文献[5-6]采用支持向量机进行入侵检测,获得了较好效果,显示了支持向量机优于其他分类算法的性能。大量研究表明[7-8],支持向量机性能与其核函数的类型、核函数参数和惩罚参数有着密切的关系,这些参数会影响SVM的分类精度及泛化性能。目前,人们往往凭经验,通过大量反复实验获得较优参数,这种方法比较费时,获得的参数不一定是最优的。近年,很多学者提出一些其他参数优化方法,文献[9]利用梯度下降法进行参数优化,虽然缩短参数搜索时间,但对初始点的选取要求较高,且是一种线性搜索方法,极易陷入局部最优;文献[10-11]利用遗传算法、文献[12-13]利用蚁群算法对SVM参数进行优化选择,这些智能方法虽然降低了对初值选择的依赖性,但算法原理和思想比较复杂,对不同的优化问题都需要设计不同的交叉、变异和选择方式,且也易陷入局部最优。粒子群(ParticleSwarm Optimization,PSO)[14-15]算法是一种有效的全局寻优算法,通过种群中粒子之间的竞争与合作产生的群体智能来指导优化搜索过程寻找最优解,相对上述其他方法具有概念简单、效率高及容易实现的特性。本文采用粒子群算法优化支持向量机的参数,以提高算法的泛化性能。
入侵检测数据的属性中并非所有属性对入侵检测都是有效或起决定性作用的,而且含有大量噪声,同时属性之间也存在一定的冗余,这会降低检测精度,所以属性约简是提高入侵检测性能的有效途径。主成分分析、聚类、粗糙集、信息增益等是目前常用的属性压缩或约简方法。粗糙集(Rough Set,RS)[16]是建立在离散空间等价关系上的专门研究不精确性和不确定性知识的数学工具,其核心是知识约简,生成规则中包含了对分类起着不可或缺的条件属性。蔡忠闽等[16-18]将粗糙集应用于入侵检测,进一步提高检测效果。但传统粗糙集不能直接处理连续型数据,需要对连续属性进行离散化,这一处理过程必然会带来信息丢失,检测结果受离散化处理技术的影响很大并且降低了检测精度。邻域粗糙集(Neighborhood Rough Set)[19-21]是一种在经典粗糙集理论基础上发展起来的能够直接处理连续型数据的方法,它不需要事先对连续数据进行离散化处理,在约简之前不存在离散化带来的信息损失问题,使选择得到的属性子集具有更强的分类能力。
基于以上分析,本文融合了邻域粗糙集与粒子群进行入侵检测。首先采用邻域粗糙集方法对原始训练集进行属性约简,消除噪声及冗余属性,然后再使用经粒子群优化核函数、惩罚等参数的支持向量机进行训练与测试。本文并在KDD99数据集进行仿真实验来验证本文算法的有效性和优越性。
2 本文算法
2.1 基于邻域粗糙集的属性约简
入侵检测数据具有高维大样本特征,这就使得机器学习过程中存在如下两方面的问题:首先入侵检测数据集中存在大量噪声及冗余属性,严重影响分类器的分类精度;其次,机器学习算法的训练和分类时间随数据维数的增加而增加,会降低分类算法的效率。大量研究证明,进行属性约简是提高分类器分类精度、提高算法效率的有效方法。
粗糙集理论[16]是由波兰学者Pawlak于1982年提出的一种有效处理不完整、不精确信息的数学分析工具,该理论的特性是不需要任何先验信息,仅使用数据本身的内部信息便能从中发现隐含知识,揭示潜在规律,对不完整不精确数据进行有效处理。传统粗糙集理论首先要将连续数据离散化,这样会导致原始信息的丢失,计算处理的结果在很大程度上取决于离散化的效果。邻域粗糙集[19-21]是胡清华在经典粗糙集理论模型的基础上发展起来的能够直接处理连续型数据的方法,它不需要事先对连续型数据进行离散化处理,可直接用于知识约简等问题。因此,为保证入侵检测的准确性和原始信息的完整性,本文采用邻域粗糙集方法进行属性约简,在此基础上对入侵检测信息样本空间进行邻域粒化,直接计算样本距离,确定样本之间相邻关系。

如果∀si∈S且B∈G,样本si在子属性空间B中的邻域记为δB(si),则δB(si)={sj|sj∈S,ΔB(si,sj)≤δ},其中δ是一个预设的阈值,ΔB(si,sj)是在子属性空间B中的一个测度函数。通常使用的测度函数有:Manhattan距离、Euclidean距离和Chebychev距离。设s1和s2表示n维属性空间G={g1,g2,…,gn}中的两个样本,f(s,gi)表示样本s在第i维属性gi的值,则Minkowsky距离可定义为:,当p=1,则称之为Manhattan距离Δ1;p=2,则称之为Euclidean距离 Δ2;p=∞,则称之为Chebychev距离Δ∞。


设a∈B,则属性的重要度定义为:
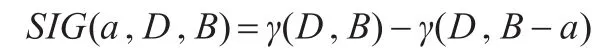
邻域粗糙集属性约简算法:

算法结束
2.2 基于粒子群优化的支持向量机参数选择
2.2.1 支持向量机
支持向量机[1-2]是一种基于统计学习理论的机器学习方法,以结构风险最小化为准则,较好地解决了高维、非线性、小样本等问题。基本思想是基于Mercer定理,通过适当的非线性变换将输入空间变换到一个高维特征空间,把在这个特征空间中寻找线性回归最优超平面归结为求解凸规划问题,并求得全局最优解。
对于给定样本点:

(1)线性可分。问题便归结为以下优化问题

判别函数:

为了求解式(2),使用Wolfe对偶定理把上述问题转化为其对偶问题进行求解:
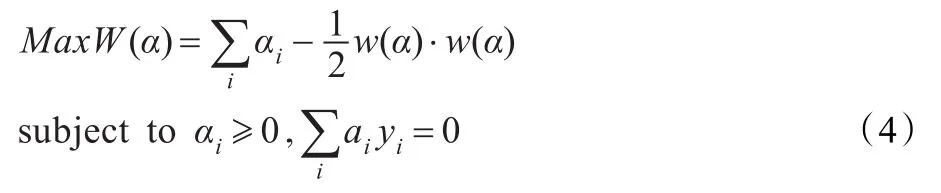
(2)线性不可分。引入松弛变量ξi,把式(2)改写为下面的求解问题。

类似的可以得到相应的对偶问题:

对式(4)、(6)的求解是一个典型的有约束的二次优化问题,已经有了很多成熟的求解算法。
2.2.2 粒子群算法
Eberhart于1995年提出了基于鸟群觅食行为的粒子群优化算法[14],由于该算法概念简明、实现方便、收敛速度快、参数设置少,是一种高效的优化算法。在粒子群算法中,每个个体称为一个“粒子”,其实每个粒子代表着一个潜在的解。在一个D维的目标搜索空间中,每个粒子看成是空间内的一个点。设群体由m个粒子构成。m也被称为群体规模,它的取值会影响算法的运算速度和收敛性。
PSO算法的数学描述为:设在一个D维空间中,由m个粒子组成的种群X=(x1,…,xi,…,xm),其中第i个粒子位置为xi=(xi1,xi2,…,xiD)T,其速度为Vi=(vi1,vi2,…,vid,…,viD)T。它的个体极值为pibest=(pi1,pi2,…,piD)T,种群的全局极值为pgbest=(pg1,pg2,…,pgD)T,按照追随当前最优例子的原理,粒子xi将按式(7)、(8)改变自己速度和位置。

式中j=1,2,…,D,i=1,2,…,m,m为种群规模,t为当前进化代数,r1,r2为分布于[ ] 0,1之间的随机数;c1,c2为加速因子,ω为权重向量。
2.2.3 基于粒子群算法的SVM参数优化算法
研究表明,支持向量机核函数及相关参数、惩罚参数是影响其分类性能的关键因素。其中,惩罚系数C反映了算法对离群样本数据的惩罚程度,其值影响模型的复杂性和稳定性。C过小,对超出离群样本点惩罚就小,训练误差变大;C过大,学习精度相应提高,但模型的泛化能力变差。C的值影响到对样本中“离群点”(噪声影响下非正常数据点)的处理,选取合适的C就能在一定程度提高抗干扰能力,从而保证模型的稳定性。
径向基K(x,y)=exp(-‖x-y‖2/σ2)是应用最广泛的核函数,无论是低维、高维、小样本、大样本等情况,RBF核函数均适用,具有较宽的收敛域,是较为理想的核函数。核函数的宽度系数σ反映了支持向量之间的相关程度。σ很小,支持向量间的联系比较松弛,学习机器相对复杂,推广能力得不到保证;σ太大,支持向量间的影响过强,难以达到足够的精度。
因此核函数参数σ和惩罚参数C是影响支持向量机分类精度的重要因素。本文将采用粒子群算法搜索一组最优的惩罚系数、核参数{ }C,σ,使得支持向量机的分类精度最高。以支持向量机在训练集上的交叉验证误差为适应度函数。算法具体步骤如下:
步骤1种群初始化与参数设置:种群粒子初始化{C,σ},种群规模m,迭代次数T,加速因子c1,c2,权重因子ω。
步骤2计算初始粒子的适应度值并进行比较,取适应度最好的粒子(即适应度最小的粒子)所对应的个体极值作为最初的全局极值pgbest。
步骤3按照式(7)与式(8)进行迭代计算,更新粒子的位置、速度。
步骤4计算当前粒子的适应度。
步骤5将每个粒子的适应度值与其pibest对应的适应度值比较,若优,更新pibest,否则保留原值。
步骤6将更新后的每个粒子的pibest与全局极值pgbest比较,若优,更新pgbest,否则保留原值。
步骤7判断是否满足终止条件,若达到最大迭代次数T,或所得最优粒子不再变化就终止迭代,否则返回到步骤3。
2.3 本文算法的步骤与框架
步骤1利用邻域粗糙集对训练集进行属性约简,产生约简的训练集。
步骤2在产生的训练集上利用粒子群算法优化支持向量机参数,获得最优(C,σ)。
步骤3将(C,σ)作为支持向量机的参数,在约简的训练集上进行训练,并在测试集上进行测试。
本文算法框架如图1所示。
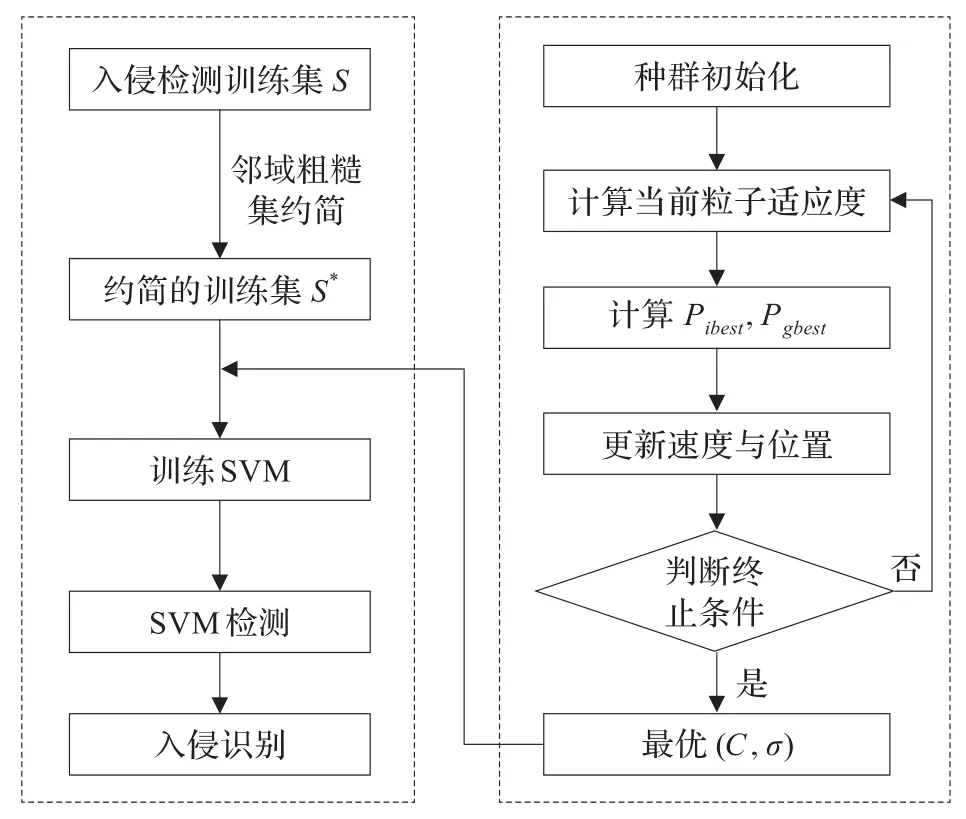
图1 本文算法框架
3 仿真实验及结果分析
3.1 实验数据
选取KDD CUP 99数据集中的10%数据集作为实验数据集。10%数据集包括训练集和测试集两部分,从10%数据集的训练集中随机抽取1 000个样本作为训练数据,其中包含入侵数据195个,其中包含四大类攻击11种,具体为Dos攻击有ueptne攻击40个、smurf攻击90个、back攻击6个,probing攻击有ipsweep攻击10个、portsweep攻击10个、satan攻击15个,U2R攻击有buffer_overflow攻击4个、rootkit攻击4个,R2L攻击有waremster攻击4个、Guess_passwd攻击6个、warezclient攻击6个。从10%数据集的训练集中随机抽取800个样本分别作为测试数据,其中已知攻击100个,为验证算法对未知攻击的检测效果,加入未知攻击100个。
为验证本文算法对未知攻击的检测能力,在测试数据集中加训练集中没有的攻击类型,分为4大类10种,分别为Dos攻击有teardrop10个、pod20个、land5个,probing攻击有nmap10个,U2R攻击有loadmodule2个、perl2个,R2L攻击有spy2个、phf2个、imap5个、multihop2个、ftp_write2个,测试集数据共包含攻击类型21种。
3.2 算法评价标准
入侵检测系统的性能评价指标主要有两个:检测率、误警率。

3.3 实验方法
为了研究算法的稳定性,实验重复100次,取其平均值作为实验结果。其中:
算法1:直接采用SVM进行分类(该算法中SVM参数随机生成)。
算法2:先采用粗糙集进行属性约简,然后利用SVM进行分类(算法中SVM参数随机生成)。
算法3:先采用邻域粗糙集进行属性约简,然后利用SVM分类(该算法中SVM参数随机生成)。
本文算法:先用邻域粗糙集进行属性约简,然后使用PSO优化SVM参数,最后利用SVM分类。
3.4 实验结果与分析
3.4.1 邻域粗糙集半径与入侵检测精度
在算法3与本文算法中,需要设置邻域粗糙集的半径,半径的不同会导致分类精度的差异,这里设置邻域半径在0.01到1之间,以0.01为步长的方式取值,对于邻域半径每一个取值,算法都得到一个属性子集,共获得100个属性子集。
图2、3分别直观地显示了入侵检测率、误警率与邻域半径之间的关系。从图2可以看出半径在0.01到0.24之间的时候,其入侵检测率保持在81%左右,而当半径增加到0.27到0.48之间时,检测率有大幅提高,大概在92%左右,说明邻域半径对检测率的影响是较大的。从图3看到,半径在0.01到0.48之间的时候,其误警率基本保持在2%左右,而0.48到0.6,误警率大幅增加。

图2 邻域粗糙集半径与入侵检测率关系

图3 邻域粗糙集半径与入侵误警率关系
综合以上分析可得,当邻域半径在0.3到0.48与0.6到0.66之间的时候,其检测率较高,同时误警率达到较低的状态,这为邻域粗糙集的使用提供一定借鉴。
3.4.2 不同算法的检测精度比较
粒子群算法中的参数设置如下:c1为1.5,c2为1.7,最大进化代数为200,种群规模为20,k为0.6,速率更新公式中速度前面的弹性系数为1,种群更新公式中速度前面的弹性系数为1,SVM Cross Validation参数为3,SVM参数c的变化范围为[0.1,100],SVM参数δ的变化范围为[0.01,1 000]。

表1 算法1、算法2、算法3与本文算法的实验结果 (%)

表2 不同算法对已知、未知攻击的平均检测率 (%)
表1给出了四种不同算法的实验结果。可以看到,本文算法的检测率平均值与最优值是四种算法中最高的,同时误警率是最低的。算法2采用了粗糙集对数据集进行了属性约简,使得检测率相对算法1提高约3%左右,说明通过属性约简可以剔除部分噪声和冗余属性,提高入侵检测效果;算法3检测率相对算法2提高约4%左右,说明了邻域粗糙集直接对连续型数据进行处理,避免传统粗糙集离散化过程中带来的信息损失,入侵检测效果进一步提高;当SVM参数C=1.47,σ=4.09,邻域粗糙集半径取0.31,本文算法的入侵检测率最优值达到95.42%,误警率到达0.81%,其检测性能优于其他算法,主要是SVM参数的选择对于增强分类器的泛化性能具有很大的影响,最终导致检测性能的大幅提高。
表2给出四种算法在已知、未知攻击上的检测率。发现本文算法对已知攻击和未知攻击检测上都有大幅度的提高,充分说明了该算法对未知攻击检测的有效性,算法具有较强的泛化性能和鲁棒性。
3.4.3 稳定性分析
图4显示了四种不同算法的稳定性。可以清楚地看出本文算法在稳定性以及精确率两方面都远优于其他算法,具有更好的泛化性能和鲁棒性。
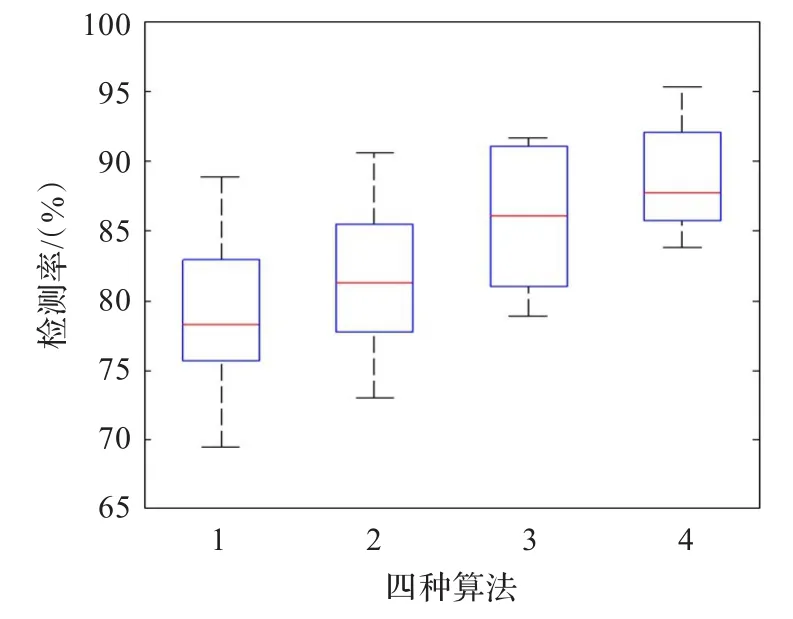
图4 四种不同算法的稳定性与精度比较
4 结论
入侵检测数据往往具有噪声和冗余属性,并且部分属性数据具有连续性,为了克服连续属性离散化过程中带来的信息损失,本文采用邻域粗糙集模型进行属性约简,并使用粒子群算法优化支持向量机核函数参数和惩罚参数,在KDD99数据集上的仿真实验结果表明本文算法可以进一步提高入侵检测率并同时降低误警率,该算法具有较强的泛化性能和鲁棒性。
[1]Sanchez A D.Advanced support vector machines and kernel methods[J].Neurocomputing.2003,55(1):15-20.
[2]陈涛.选择性支持向量机集成算法[J].计算机工程与设计,2011(5):259-263.
[3]陈涛.基于双重扰动的支持向量机集成[J].计算机应用,2011,28(1):46-49.
[4]陈涛.基于加速遗传算法的选择性支持向量机集成[J].计算机应用研究,2011,32(2):57-61.
[5]陈光英,张千里,李星,等.基于SVM分类机的入侵检测系统[J].通信学报,2002,23(5):51-56.
[6]饶鲜,董春曦,杨绍全,等.基于支持向量机的入侵检测系统[J].软件学报,2003,14(4):798-803.
[7]陈涛.基于差分进化算法的支持向量回归机参数优化[J].计算机仿真,2011(6):674-679.
[8]陈涛,雍龙泉,邓方安,等.基于差分进化算法的支持向量机参数选择[J].计算机工程与应用,2011,47(5):24-26.
[9]Chappelle O.Choosing multiple parameters for support vector machines[J].Machine Learning,2002,46(1):131-160.
[10]Zheng Chunhong,Jiao Licheng.Automatic parameters selection for SVM based on GA[C]//Proceedings of the 5th World Congress on Intelligent Control and Automation.Piscataway,NJ:IEEE Press,2004:1869-1872.
[11]杨洁.基于遗传算法的SVM带权特征和模型参数优化[J].计算机仿真,2008(9):48-51.
[12]齐亮.基于蚁群算法的支持向量机参数选择方法研究[J].系统仿真技术,2008(11):34-38.
[13]秦军立,倪世宏,苏晨.基于蚁群优化SVM及其应用研究[J].计算机仿真,2009(11):46-49.
[14]Fukuyama Y.Fundamentals of particle swarm optimization techniques[M]//Modern Heuristic Optimization Techniques:Theory and Applications to Power Systems.[S.l.]:IEEE Power Engineering Society,2002:45-51.
[15]Shao Xinguang,Yang Huizhong,Chen Gang.Parameters selection and application of support vector machines based on particle swarm optimization algorithm[J].Control Theory and Applications,2006,23(5):740-743.
[16]张义荣,鲜明,肖顺平,等.一种基于粗糙集属性约简的支持向量异常入侵检测方法[J].计算机科学,2006,33(6):64-68.
[17]赵曦滨,井然哲,顾明,等.基于粗糙集的自适应入侵检测算法[J].清华大学学报,2008,48(7):1158-1168.
[18]陈涛.基于动态粗糙集约简的选择性支持向量机集成[J].计算机仿真,2012,43(2):328-331.
[19]胡清华,于达仁,谢宗霞,等.基于邻域粒化和粗糙逼近的数值属性约简[J].软件学报,2008,15(3):121-125.
[20]胡清华,赵辉,于达仁,等.基于邻域粗糙集的符号与数值属性快速约简算法[J].模式识别与人工智能,2008,21(6):89-95.
[21]Hu Q H,Yu D R,Liu J F,et al.Neighborhood rough set based heterogeneous feature subset selection[J].Information Sciences,2008,178(18):3577-3594.
ZHAO Hui
School of Mathematics and Computer Science,Shaanxi University of Technology,Hanzhong,Shaanxi 723000,China
The intrusion detection data contains large redundant and noisy features,as well as some continuous attributes.This paper presents an algorithm based on neighborhood rough set and Particle Swarm Optimization algorithm for the effect of intrusion detection.Training subset is reduced by using neighborhood rough set,and new training subset is generated.The redundant attributes and noise are eliminated to avoid information loss when using traditional rough set;parameters of Support Vector Machine are optimized using particle swarm algorithm to avoid the risk of low precision by subjective choiced parameters.It improves the performance of the intrusion detection.The simulation results in the KDD99 dataset show that the algorithm can effectively improve the accuracy and efficiency of intrusion detection.It has high generalization and stability.
network intrusion detection;neighborhood rough set;Support Vector Machine(SVM);Particle Swarm Optimization(PSO)algorithm
入侵检测数据往往含有大量的冗余、噪音特征及部分连续型属性,为了提高网络入侵检测的效果,利用邻域粗糙集对入侵检测数据集进行属性约简,消除冗余属性及噪声,也避免了传统粗糙集在连续型属性离散化过程中带来的信息损失;使用粒子群算法优化支持向量机的核函数参数和惩罚参数,以避免靠主观选择参数带来精度较低的风险,进一步提高入侵检测的性能。仿真实验结果表明,该算法能有效提高入侵检测的精度,具有较高的泛化性和稳定性。
入侵检测;邻域粗糙集;支持向量机;粒子群算法
A
TP18
10.3778/j.issn.1002-8331.1301-0383
ZHAO Hui.Network intrusion detection algorithm based on neighborhood rough set and PSO.Computer Engineering and Applications,2013,49(18):73-77.
国家自然科学基金(No.81160183);陕西省教育厅科研基金(No.12JK0864);陕西理工学院科研基金(No.SLGKY11-08)。
赵晖(1979—),男,讲师,研究方向为数据挖掘、网络安全。E-mail:zh911@sina.com
2013-02-01
2013-03-18
1002-8331(2013)18-0073-05
CNKI出版日期:2013-04-08 http://www.cnki.net/kcms/detail/11.2127.TP.20130408.1646.001.html

