基于目标函数变化率的混合蚁群遗传算法

刘雪东，许 峰

1.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001

2.安徽理工大学 理学院，安徽 淮南 232001

基于目标函数变化率的混合蚁群遗传算法

刘雪东1，许 峰2

1.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001

2.安徽理工大学 理学院，安徽 淮南 232001

1 引言

随着生命科学的迅猛发展，社会性动物（如蚂蚁、鸟群、鱼群等）的自组织行为引起了人们的广泛关注。许多学者对这些动物的行为进行数学建模并用计算机对其进行仿真，群智能算法应运而生。

蚁群算法（Ant Colony Optimization，ACO）是近年来颇受国内外学者关注的一种新型模拟进化算法，由意大利学者Dorigo M于1992年首先提出[1]，Nature曾多次对蚁群算法的研究成果进行报道[2-4]。蚁群算法用蚁群在搜索食物过程中所体现出的寻优能力来解决优化问题，其算法的基本思想是模仿蚂蚁依赖信息素，通过蚂蚁间正反馈的方法来引导每个个体的行为。

遗传算法（Genetic Algorithm，GA）于1975年由美国Michigen大学的J.Holland教授等人受生物进化论的启发而提出的[5]。遗传算法把生物进化过程中的自然选择、优胜劣汰、适者生存和遗传变异的思想应用到优化问题中，是一种全局随机搜索算法。

蚁群算法具有分布式、自组织、正反馈等优点，缺陷是收敛速度较慢，易陷于局部最优解。遗传算法的优点是自适应、并行性、具有较强的全局收敛性，缺陷是局部搜索能力较弱。

将两种或多种智能优化算法按照某种规则相融合或在某种智能算法中引入其他优化思想，形成混合优化思想，可以有效地扬长避短，充分发挥智能算法的优点，大大提高算法的各方面性能[6]。

考虑到蚁群算法和遗传算法在收敛性上的互补性，有多位学者陆续提出了基于蚁群算法和遗传算法的混合优化算法[6]。这些混合算法通常采用固定进化代数来控制两种算法的调用，很有可能造成已经早熟的种群还在进行无用的进化，影响算法的收敛速度。本文提出了一种基于目标函数变化率的混合蚁群遗传算法，在进化过程中，根据目标函数的变化率动态地控制蚁群算法和遗传算法的调用次数，并根据数值实验结果对新算法的全局和局部收敛性进行了评测。

2 蚁群算法和遗传算法

2.1 蚁群算法

用于优化领域的蚁群算法吸收了生物界中蚂蚁群体的行为特征，其基本原理是：

（1）蚂蚁能感知小范围区域内的状况，并判断出是否有食物或其他同伴的信息素轨迹；

（2）蚂蚁能连续不断地释放自己的信息素；

（3）蚂蚁释放的信息素浓度随时间逐步减小。

蚂蚁有能力在没有任何提示下找到从其巢穴到食物的最短路径，并且能随环境的变化而变化，适应性地搜索新的路径，产生新的选择。其根本原因是蚂蚁在寻找食物时，能在其走过的路上释放信息素，随着时间的推移该物质会逐渐挥发。当一定路径上通过的蚂蚁越来越多时，其留下的信息素也越来越多，后来的蚂蚁选择该路径的概率也越高，从而更增加了该路径的信息素强度。而强度大的信息素会吸引更多的蚂蚁，从而形成一种正反馈机制。通过这种正反馈机制，蚂蚁最终可以发现最短路径。特别地，当蚂蚁巢穴与食物间出现障碍物时，蚂蚁不仅可以绕过障碍物，而且通过蚁群信息素在不同路径上的变化，经过一段时间的正反馈，最终收敛到最短路径。

蚁群算法在不同问题中有不同的表现形式，但其核心步骤均为信息素轨迹强度的更新方式和蚂蚁转移概率的确定。本文采用下列蚂蚁圈模型[7]：

若路径(i，j)在t时刻信息素轨迹强度为τij，蚂蚁k在路径(i，j)上留下的单位长度轨迹信息素数量为，轨迹的持久性为ρ(0≤ρ＜1)，则轨迹强度的更新方程为：

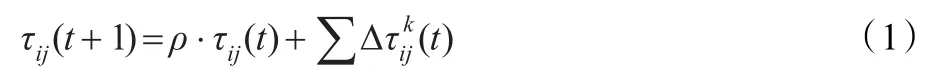
设Zk为第k只蚂蚁在本次循环中所走的路径的长度，则其中Q为一个常数。如果设ηij为路径(i，j)的能见度，通常取为1/dij，dij为路径(i，j)的长度，路径可见度的相对重要性为β(β≥0)，路径轨迹的相对重要性为α(α≥0)，U为可行顶点集，则蚂蚁k在t时刻的转移概率为：

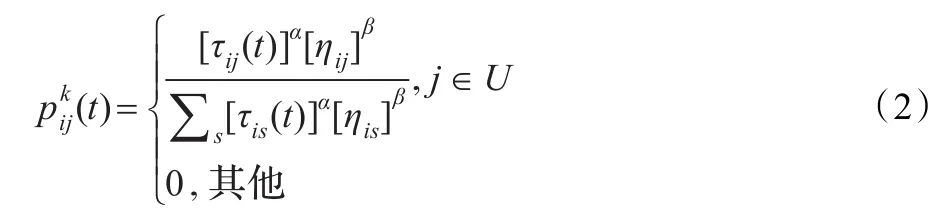
2.2 遗传算法

遗传算法的运算对象是由个体组成的群体。在遗传算法的运算过程中，群体按照优胜劣汰的法则进行遗传和进化，将适应度较高的个体更多地遗传到下一代，经过若干代进化后，在群体中会得到一个或一批优良的个体，它们即对应问题的最优解。

生物的进化主要是通过染色体之间的交叉和染色体的变异来完成的。遗传算法模拟这个进化过程，对群体使用遗传算子，从而得出新一代群体。

基本遗传算法的运算过程如下：

（1）选取适当的群体规模Μ、染色体编码长度l、进化代数T、交叉概率Pc、变异概率Pm等参数，随机生成规模为Μ的初始群体P(t)，t=0；

（2）解码并计算适应度；

（3）进行选择操作；

（4）进行交叉操作；

（5）进行变异操作，产生新一代种群P(t+1)；

（6）若t＜T，则t=t+1，转（2），否则输出最优解，停机。

3 混合蚁群遗传算法

蚁群算法已被证明是一种很有发展前景的求解复杂优化问题（特别是离散优化问题）的有效方法。但与其他智能优化方法一样，蚁群算法不可避免地存在着一些缺陷，如初始信息素生成速度较慢，全局收敛性较差，易早熟等。

近年来，许多学者将蚁群算法与其他优化算法相融合，相继提出了多种混合蚁群算法，并将其应用于不同的领域，取得了较好的效果。刘波将分布估计思想引入蚁群算法[8]；陈立华和张潇提出了含有变异算子的混合蚁群算法，并将其应用于水库群优化[9-10]；梁亮将Markov过程与蚁群算法相结合[11]；周永务在蚁群算法中引入2-opt算法，并将其应用于多时间窗车辆路径问题[12]；杜占玮提出了基于互信息的混合蚁群算法[13]；税薇提出了与人工势场相结合的混合蚁群算法[14]；丁建立[15]提出采用遗传算法生成信息素分布，利用蚂蚁算法求精确解，优势互补；毛宁[16]提出借助遗传算法中的变异帮助蚁群算法提高跳出局部最优解的能力；梁旭[17]提出了一种动态蚁群混合遗传算法，大大提高了蚁群算法的收敛速度。

本文提出一种基于目标函数变化率的动态混合蚁群遗传算法（Dynamic Ant Colony Genetic Algorithm，DACGA），其基本思想是：根据目标函数的变化率交叉地调用蚁群算法和遗传算法。用蚁群算法的解作为遗传操作的种子，每当种群进化接近停滞时，调用蚁群算法。这种方法可动态地控制蚁群算法和遗传算法的调用时机，再配合相应的信息素更新方法，可以提高算法的收敛性。

动态调用蚁群算法和遗传算法的具体方法是：

定义：

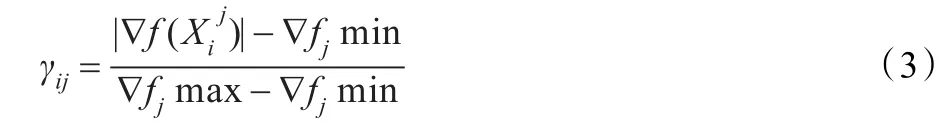
其中：

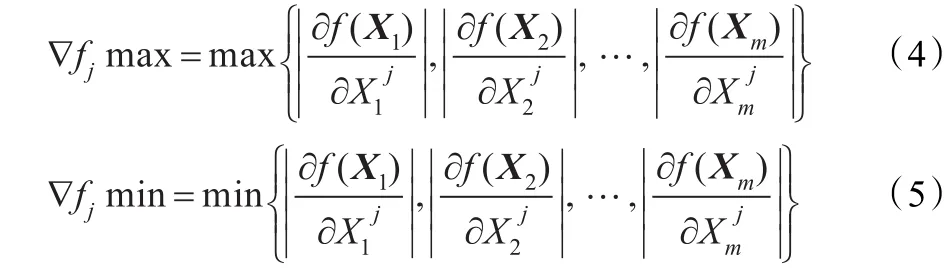
(i=1,2,…,m;j=1,2,…,n)表示向量Xi的第j个分量。

对于离散优化问题，f(X)不存在梯度，则

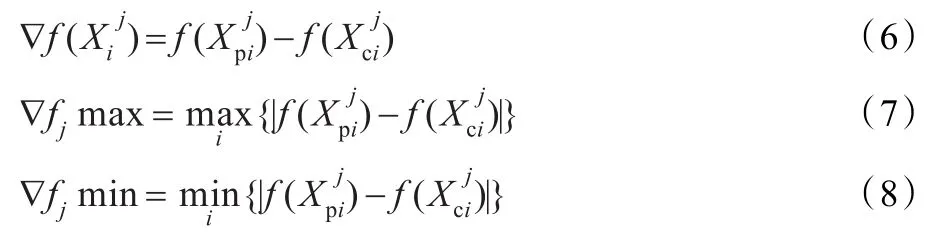
其中，Xp，Xc分别表示父代和子代个体。

当γij小于设定的阈值ε（通常取为10-2）时，选择蚁群算法，否则选择遗传算法。

DACGA的流程如下：

（1）取定参数NGmin，NGmax，NKmax，α，β，ρ。

（2）蚂蚁位置初始化。

（3）利用式（1）更新信息素，并转（5），否则转（4）。

（4）根据式（2）选择下一节点。

（5）将蚂蚁搜索到的初始解和全局最优解作为遗传算法的初始种群，进行选择、交叉、变异，更新种群。

（6）当遗传算法达到最小迭代次数NGmin时，则根据前述方法动态选择蚁群算法或遗传算法。若选择调用蚁群算法，则利用式（1）更新信息素，并转（8）。

（7）当遗传算法达到最大迭代次数NGmax时，则转（8），否则继续遗传操作。

（8）若混合算法的整体迭代次数达到NKmax，则输出最优解，算法结束，否则转（2）。

4 算法的收敛性分析与性能评测

4.1 收敛性分析

混合蚁群遗传算法的收敛性极为复杂，尚未完全解决。目前公认的结论是[18]：基于蚂蚁圈模型的蚁群算法和基本遗传算法的混合算法是收敛的。

由于本文采用的是基于蚂蚁圈模型的蚁群算法和基本遗传算法，只是对调用两种算法的条件作了改进，所以本文提出的算法在理论上是收敛的。

4.2 性能评测

鉴于混合优化算法已被公认为解决车间调度问题较为有效的方法[19]，下面用基于目标函数变化率的DACGA算法对车间调度问题中的两个基准测试问题FT06和FT10[19]进行仿真计算，并将计算结果与基本蚁群算法、基本遗传算法和一种蚁群遗传混合算法[16]（Ant Colony System Genetic Algorithm，ACSGA）的计算结果进行比较，从而检验新算法的收敛性能。

仿真程序采用Matlab编程，遗传算法中，编码长度为10，种群规模为50，交叉概率为0.85，变异概率为0.1，NGmin=20，NGmax=50；蚁群算法中，α=1，β=1，ρ=0.5，Q=800，NKmax=300；动态调用阈值ε=0.01。

考虑到计算结果的随机性，表1和表2中给出的是20次实验结果的平均值。

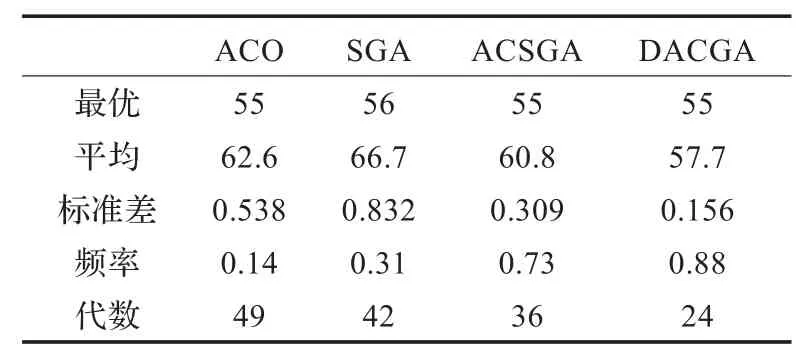
表1 FT06的优化指标结果

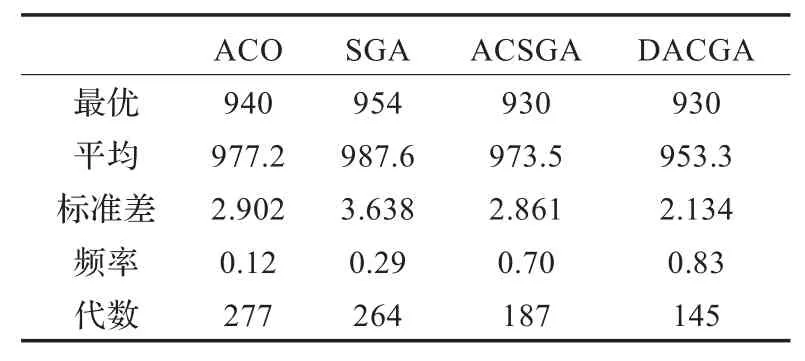
表2 FT10的优化指标结果

表1和表2中分别给出了FT06和FT10的最优值、平均值、标准差、20次仿真中求得最优值（达到理论最优解的95%即视为最优值）的频率及最小进化代数。FT06和FT10的理论最优解分别为55和930。

为了更直观地反映DACGA在收敛性方面的改进，图1给出了DACGA与ACSGA求解FT10的对比进化曲线。

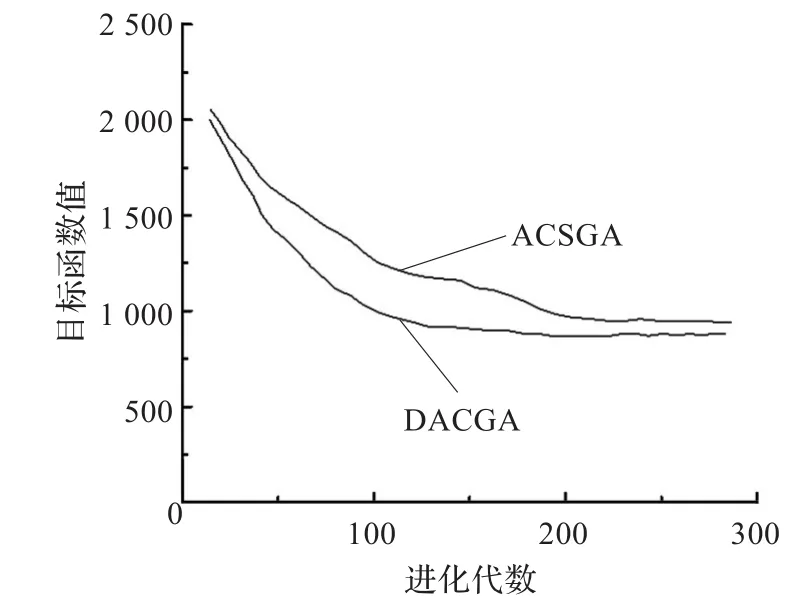
图1 FT10的DACGA和ACSGA进化曲线

从表1、表2和图1中可以很清楚地看出：

（1）ACO在最优值、平均值和标准差指标上优于SGA，而SGA在收敛频率和进化代数指标方面优于ACO，即ACO局部收敛性较强而全局收敛性较弱，SGA全局收敛性较强而局部收敛性较弱。

（2）ACSGA和DACGA在所有指标中均较ACO和SGA为优，即混合蚁群遗传算法的确可以优势互补，提高收敛性。

（3）相比较而言，DACGA较ACSGA在收敛性和收敛速度方面又有一定程度的提高。这表明，本文提出的ACO和SGA的动态调用机制是有效的。

5 结束语

通过对蚁群算法和遗传算法收敛性特点的分析，设计了一种基于目标函数变化率的算法调用机制，提出了一种新的混合蚁群遗传算法。新算法不仅实现了蚁群算法和遗传算法的优势互补，而且通过动态调用两种算法减少了冗余迭代次数，提高了收敛速度。数值仿真结果显示，新算法与蚁群算法相比有较强的全局收敛性，而与遗传算法相比则有较强的局部收敛性。

最后要特别指出的是，蚁群算法与粒子群算法、人工免疫系统、分布估计算法、协同进化算法等均为近年来出现的新型进化范例，理论体系尚不完善，收敛性等关键理论问题有待进一步研究。

[1]Dorigo M.Optimization，learning and natural algorithms[D]. Dipartimento di Elettronica，Politecnico di Milano，Italy，1992.

[2]Bonabeau E，Dorigo M，Theraulaz G.Inspiration for optimization from social insect behavior[J].Nature，2000，406（6）：39-42.

[3]Michael J B K，Jean-Bernarrd B，Laurent K.Ant-like task and recruitment in cooperation robots[J].Nature，2000，406（31）：992-995.

[4]Jackson D E，Holcombe M，Ratnieks F L W.Trail geometry gives polarity to ant foraging networks[J].Nature，2004，432（7019）：907-909.

[5]Holland J H.Adaptation in natural and artificial system[M]. Ann Arbor：The University of Michigan Press，1975.

[6]梁旭，黄明.现代智能优化混合算法及其应用[M].北京：电子工业出版社，2011.

[7]Dorigo M，Bonabeau E，Theraulaz G.Ant algorithms and stigmergy[J].Future Generation Computer System，2000，16（8）：851-871.

[8]刘波，李惠光，吴惕华，等.一种新的混合蚁群算法[J].数学的实践与认识，2009，39（6）：154-161.

[9]陈立华，梅亚东，杨娜，等.混合蚁群算法在水库群优化调度中的应用[J].武汉大学学报，2009，42（5）：661-665.

[10]张潇，王江晴.混合蚁群算法在车辆路径问题中的应用[J].计算机工程，2011，37（24）：190-192.

[11]梁亮，郭波.基于混合蚁群算法的产品开发过程优化方法[J].系统工程理论与实践，2009，29（10）：118-128.

[12]彭碧涛，周永务.多时间窗车辆路径问题的混合蚁群算法[J].计算机工程与应用，2010，46（31）：28-31.

[13]杜占玮，杨永健，孙永雄，等.基于互信息的混合蚁群算法及其在旅行商问题上的应用[J].东南大学学报，2011，41（3）：478-481.

[14]税薇，葛艳，韩玉，等.基于混合蚁群算法的无人机航路规划系统[J].仿真学报，2011，23（3）：574-577.

[15]丁建立，陈增强，袁著祉.遗传算法与蚂蚁算法的融合[J].计算机研究与发展，2003，40（9）：1351-1356.

[16]毛宁，顾军华.蚁群遗传混合算法[J].计算机应用，2006，26（7）：1692-1694.

[17]梁旭，刘鹏飞，黄明.一种新的蚂蚁遗传混合算法应用研究[J].计算机集成制造系统，2008，14（8）：1566-1570.

[18]丁建立，陈增强，袁著祉.遗传算法与蚂蚁算法的融合的马尔可夫收敛性分析[J].自动化学报，2004，30（4）：629-634.

[19]王凌.车间调度及其遗传算法[M].北京：清华大学出版社，2003：58-59.

LIU Xuedong1,XU Feng2

1.School of Computer Science and Engineering,Anhui University of Science and Technology,Huainan,Anhui 232001,China
2.School of Science,Anhui University of Science and Technology,Huainan,Anhui 232001,China

According to the complementary on convergence of ant colony algorithm and genetic algorithm,a hybrid ant colony genetic algorithm based on the change rate of objective function is put forward.The basic idea of new algorithm is that the solutions of ant colony algorithm are given as the initial population of genetic algorithm,and the ant colony algorithm and genetic algorithm are dynamically called according to the change rate of objective function.When population evolutionary is close to stagnation, ant colony algorithm is called.This approach can dynamically control the call timing of ant colony algorithm and genetic algorithm. Together with the pheromone update methods,the convergence of hybrid algorithm is improved.The new algorithm is used to solve the Job shop scheduling benchmarks problem,and the simulation results show that the global and local convergence performance of new algorithm has been significantly improved compared with basic hybrid ant colony genetic algorithm.

Ant Colony Optimization（ACO）;Genetic Algorithm（GA）;change rate of objective function;Job shop scheduling benchmarks problem

根据蚁群算法和遗传算法收敛性互补的特点，提出了一种基于目标函数变化率的混合蚁群遗传算法。该算法的基本思想是：用蚁群算法的解作为遗传算法的初始种群，根据目标函数的变化率交叉地调用蚁群算法和遗传算法。每当种群进化接近停滞时，调用蚁群算法。这种方法可动态地控制蚁群算法和遗传算法的调用时机，再配合相应的信息素更新方法，以提高算法的收敛性。将新算法用于车间调度基准测试问题，仿真结果表明，与常规混合蚁群遗传算法相比，新算法的全局收敛性和局部收敛性有了明显的提高。

蚁群算法；遗传算法；目标函数变化率；车间调度基准问题

A

TP301.6

10.3778/j.issn.1002-8331.1210-0278

LIU Xuedong,XU Feng.Hybrid ant colony genetic algorithm based on change rate of objective function.Computer Engineering and Applications,2013,49（18）：41-44.

安徽省教育厅自然科学基金项目（No.2010kb236）。

刘雪东（1986—），男，硕士研究生，主要研究领域为进化计算、群智能计算；许峰（1963—），男，教授，主要研究领域为进化计算、群智能计算。E-mail：fxu@aust.edu.cn

2012-10-26

2013-01-30

1002-8331（2013）18-0041-04

CNKI出版日期：2013-03-19 http://www.cnki.net/kcms/detail/11.2127.TP.20130319.1424.001.html