行星齿轮的固有特性研究❋

墨蕊娜，盛尚坤

（1.塔里木大学 机械电气化工程学院，新疆 阿拉尔 843300；2.山东光岳转向节总厂，山东 聊城 252000）

0 引言

行星齿轮传动与普通齿轮传动相比较，在相同体积和质量的情况下，能够实现更多的档位，承受更大的载荷，并且可以实现功率分流。因此，行星轮系被广泛应用于各种传动系统中。随着机械设备的高速发展，对齿轮传动系统的要求越来越高，为了避免共振就要对行星排进行固有特性计算，对系统的结构参数进行优化设计，使行星排的固有频率和激励频率合理地匹配。文献［1～8］对行星齿轮动力学固有特性进行了研究，获得了许多有益的结论。但上述文献都是针对行星轮系的某种特性工况，本文将对行星轮系在不同工况下的动态特性进行研究。

1 行星齿轮系统的力学模型的建立

图1 为行星齿轮动力学模型。行星轮系的动能和势能可以分别表示为：

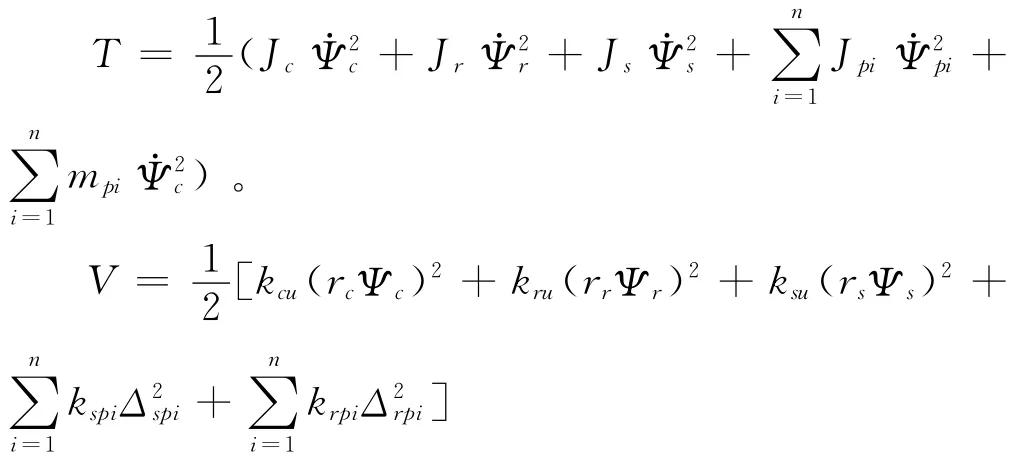
其中：Jj（j＝c，r，s，p1，p2，…，pn）分别为行星架 、内齿圈、太阳轮和各行星轮的转动惯量；Ψj分别为行星架、内齿圈、太阳轮和各行星轮的广义角位移；mpi（i＝1，2，…，n）分别为各行星轮的质量；rc为过行星轮圆心的行星架的回转半径；n为行星轮的个数；kju（j＝c，r，s）分别为行星架、内齿圈和太阳轮的扭转刚度；kspi和krpi分别为太阳轮和内齿圈与第i个行星轮的啮合刚度；Δspi和Δrpi分别为太阳轮和内齿圈与第i个行星轮啮合时沿啮合线上的相对位移。

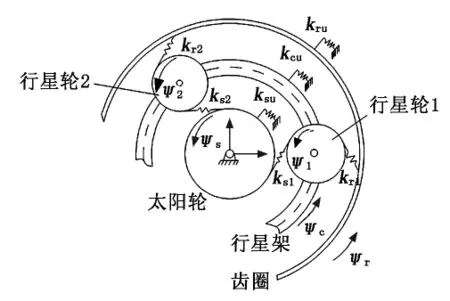
图1 行星齿轮动力学模型

运用拉格朗日方程来建立行星轮系的动力学方程：

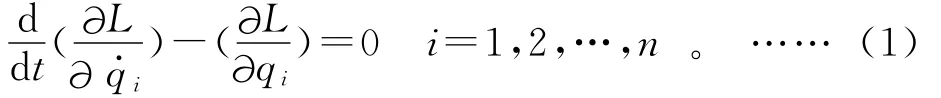
其中：L＝T－V；qi为广义坐标。

引入uj＝rjΨj（j＝c，r，s，p1，p2，…，n），得到行星轮系的无阻尼自由振动动力学方程，将动力学方程写成式（2）的形式，则系统的质量矩阵M可以用式（3）表示，刚度矩阵可以用式（4）表示。

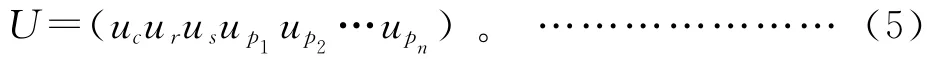
其中：α为压力角。

2 系统的固有特性分析

在研究系统的参数共振和动态特性时，需要了解系统的固有特性。本文以某风电增速箱中含有3个行星轮的行星排为例进行研究，行星轮系的基本参数见表1。

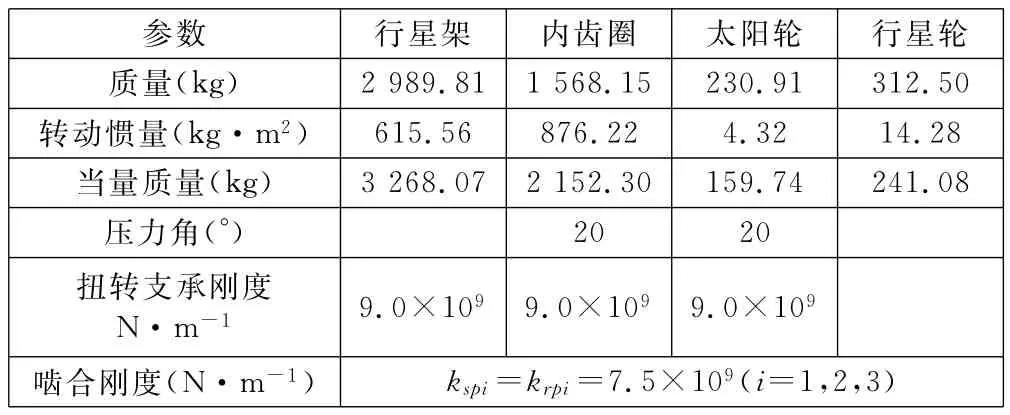
表1 某兆瓦级增速行星轮系的基本参数

本文忽略了啮合刚度的时变性，用平均啮合刚度代替啮合刚度，考虑固定基本构件内齿圈的刚度，以三行星传动为例，基于表1的数据，解式（2）得固有频率，见表2；不同工况下行星轮系的第1阶和第5阶的固有频率和经过归一化的对应振型如图2 ～图4 所示。

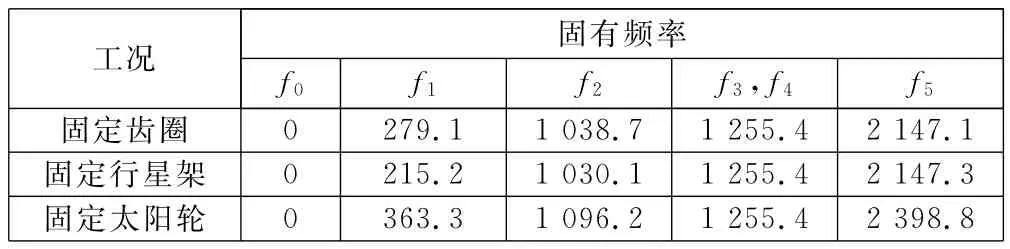
表2 不同工况下行星轮系的固有频率 Hz

由表2可知，在各种工况下均具有0频率，这表明行星轮系存在着刚体位移；在不同工况下除了具有重根的固有频率不变外，其余固有频率均发生变化。

图2 （a）、图2 （b）分别为齿圈固定时1阶、5阶频率对应的振型，其中横坐标编号1代表行星架、2代表太阳轮、3～5代表行星轮。从图2 （a）知，1阶模态中太阳轮和行星轮的振幅较大，行星架对应的振幅较小，此时修改行星架的惯量对改变1阶频率的贡献不大。从图2 （b）可以看出，在该频率下太阳轮的振幅最大，行星架的振幅接近于零，此时改变太阳轮的惯量对5阶频率的影响最大，行星轮次之，改变行星架惯量对5阶频率的影响最小。

图3 为行星架固定时1阶、5阶频率对应的振型，其中横坐标编号1代表内齿圈、2代表太阳轮、3～5代表行星轮。从图3 （a）知，1阶模态中太阳轮和行星轮的振幅较大，内齿圈对应的振幅较小，此时修改内齿圈的惯量对改变1阶频率的贡献不大。从图3 （b）可以看出，在该频率下太阳轮的振幅最大，内齿圈的振幅接近于零，此时改变太阳轮的惯量对5阶频率的影响最大，行星轮次之，改变内齿圈惯量对5阶频率的影响最小。

图2 固定齿圈时的1阶、5阶模态

图4 为太阳轮固定时1阶、5阶频率对应的振型，其中横坐标编号1代表行星架、2代表内齿圈、3～5代表行星轮。从图4 （a）知，1阶模态中行星架和行星轮的振幅较大，内齿圈对应的振幅较小，此时修改内齿圈的惯量对改变1阶频率的贡献不大。从图4 （b）可以看出，在该频率下行星轮的振幅最大，行星架的振幅次之，此时改变行星轮的惯量对5阶频率的影响最大，行星架次之，改变内齿圈惯量对5阶频率的影响最小。

3 结论

为避免行星齿轮传动中的共振现象，本文基于Lagrange方法建立了行星齿轮系统扭转振动力学模型。通过对不同工况下行星齿轮系统固有特性的计算，得出了如下结论：①不同工况下系统的固有特性各不相同，但都有零频率存在，即都存在刚体振动；②太阳轮、行星轮、行星架和内齿圈的惯量在不同工况下对行星轮系的固有频率的影响各不相同。通过比较分析可知，行星架在3种工况下振动都不是最显著的，因此改变行星架的惯量对系统频率的影响有限。

图3 固定行星架时的1阶、5阶模态

图4 固定太阳轮时的1阶、5阶模态

［1］Velex P，Flamand L.Dynamic response of planetary trains to mesh parameter excitations［J］.ASME Journal of Mechanical Design，1996，118：7-14.

［2］Lin J，Parker R G .Analytical characterization of the unique properties of planetary gear free vibration ［J］.Journal of Vibration and Acoustics，1999，121：316-321.

［3］孙智民，沈允文，李素有.封闭行星齿轮传动系统的动态特性研究［J］.机械工程学报，2002，38（2）：44-48.

［4］巫世晶，潜波，路红山，等.车辆传动系扭转振动分析系统研究与开发［J］.系统仿真学报，2006，18（11）：3100-3104.

［5］王世宇.行星传动固有特性分析［J］.中国机械工程，2005，16（16）：1461-1464.

［6］Kahraman A.Natural modes of planetary gear trains［J］.Journal of Sound and Vibration，1994，173（1）：125-130.

［7］王世宇，宋轶民，沈兆光.行星传动系统的固有特性及模态跃迁研究［J］.振动工程学报，2005，18（4）：412-417.

［8］马朝锋，刘凯，崔亚辉.风电增速箱行星轮系的扭转振动模型［J］.机械科学与技术，2010，29（6）：788-791.