连杆大端滚针轴承滚子歪斜分析

康献民，杜春英，万一夔

(五邑大学 机电工程学院，广东 江门 529020)

1 活塞连杆轴承的结构

用于活塞连杆大端的无内、外圈的滚针轴承如图1所示，连杆销的外径面为内滚道，连杆大端孔为外滚道。连杆在轴承轴线方向没有轴向约束，在工作过程中存在轴向偏移，端面会与曲轴及活塞发生摩擦[1]。文献[2-4]研究表明，连杆端面的过度磨损是导致曲柄连杆机构破坏的主要原因之一。假设连杆机构的各个轴线保持平行，那么连杆的轴向偏移与滚针轴承有必然的联系。由于滚针的径向尺寸较小,保持架引导部分的局部微小误差将对滚针的运动产生极大影响，使滚针在运动过程中出现歪斜，对连杆大端滚针轴承歪斜滚针的受力及运动进行了分析。

图1 连杆大端结构示意图

2 滚针轴承的接触特点

滚针轴承中,由于滚针直径远小于轴承滚道直径，因此曲面导向作用弱，滚针更易于发生歪斜运动，也易于发生弹性弯曲。由于滚针与滚道之间存在间隙，滚针靠保持架引导，在运动中受保持架的影响更为明显。

2.1 保持架与滚针的接触运动分析

在轴承转动时，滚针中心与保持架槽孔的中心线并不重合。当滚针中心超前于保持架槽孔中心线时(滚针在承载区时)，滚针推动保持架运动；当滚针中心滞后于保持架槽孔中心线时(滚针在非承载区时)，保持架推动滚针运动。

保持架的主要功能是保证滚针在运动中与内、外滚道为线接触状态。保持架槽孔表面存在倾斜时，会使滚针进入承载区时出现类似于螺旋滚道的受力情况。

2.2 轴承径向载荷分布

为了使滚针旋转灵活, 滚针与内、外圈和保持架之间通常有一定的间隙。在轴承的运转过程中，滚针位置不断变化使得滚针在承载区的数目呈奇、偶数交替变化。滚针轴承的径向载荷分布如图2所示[5]。

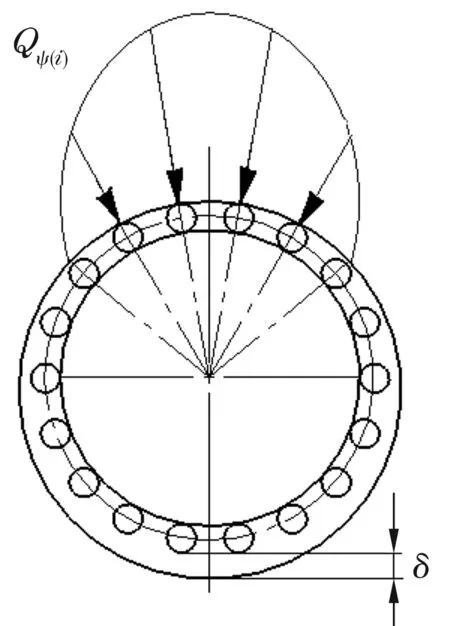
图2 滚针轴承径向载荷的分布

3 歪斜滚针的受力分析及运动分析

3.1 歪斜滚针进入承载区时的轴向摩擦力分析

当保持架引导面存在倾斜时，滚针在保持架的推动下进入承载区时，会产生歪斜，滚针轴线会与轴承轴线产生一个夹角。假设滚针左端先进入承载区(以下均基于此分析)，滚针进入承载区时，由于自身歪斜，会与滚道间产生一定的滑动摩擦，特别是端部滑动摩擦力较大。滚针进入承载区时的摩擦力及保持架作用力分布如图3所示，歪斜滚针的受力方程为

图3 滚针进入承载区时的摩擦力及保持架作用力分布

Qrf+Qrb+Febcosβ+Fef-Fif+Qψebsinβ=0，

(1)

Qψef+Qψebcosβ-Qψif-Frf-Frb-Febsinβ=0 ，

(2)

(Qrf+Qrb+Frf+Frb+Fef+Feb)rn=εnIn，

(3)

式中：Qrf为保持架对滚针左端的正压力；Qrb为保持架对滚针右端的正压力；Feb为外圈对滚针右端的摩擦力；Fef为外圈对滚针左端的摩擦力；Fif为内圈对滚针左端的摩擦力；Qψeb为外圈对滚针右端的正压力；Qψef为外圈对滚针左端的正压力；Qψif为内圈对滚针左端的正压力；Frf为保持架对滚针左端的摩擦力；Frb为保持架对滚针右端的摩擦力；εn为滚针的转动加速度；In为滚针的转动惯量；rn为从滚针中心到内、外圈接触面上点的半径；β为滚针两端相对于轴线形成的角度。

由于滚针与轴承轴线歪斜角α的存在，则滚针在轴承轴向上的受力为

∑Fxncosα+∑Fynsinα=mnan，

(4)

式中：mn为滚针质量，an为滚针发生轴向移动时的加速度。

将(1)～(2)式代入(4)式得，滚针在进入承载区时所受的轴向作用力Fxn0为

Fxn0=(Qrf+Qrb+Febcosβ+Fef+Fif+Qψebsinβ)cosα+(Qψef+Qψebcosβ-Qψif-Frf-Frb-Febsinβ)sinα=mnan。

(5)

在滚针歪斜的情况下，滚针与滚道之间的摩擦力与轴承轴线有一定的夹角，如图3所示。设内圈静止不动，外圈沿逆时针方向旋转，对于无内、外圈的滚针轴承而言，滚针在歪斜的情况下受到轴向力的作用，将发生一定的轴向偏移，轴承性能会受到影响。

3.2 歪斜滚针的回复力分析

如图4所示，在歪斜滚针进入承载区的过程中，滚针右端与外圈滚道接触，在接触部位产生微小的摩擦力，但由于歪斜滚针右端没有接触内圈滚道，故没有摩擦力作用。根据力矩平衡原理，滚针在进入承载区的过程中，由于摩擦力的作用，滚针的歪斜角度会减小并最终消除。

图4 滚针在承载区回复过程的受力分析

在承载区，该回复作用力最终使滚针轴线回复到与轴承轴线平行的状态。设滚针在开始进入承载区时为起点，滚针脱离保持架的推力作用后，由于在左端受滚道的作用，以该接触点为回转中心，在右端的回复力的作用下，向减小歪斜角方向转动，由图4可得回复扭转力矩Mnf为

Mnf(t)=μKμQψeb(t)l(t) ，

(6)

式中：Kμ为变形接触系数；μ滑动摩擦因数；l(t)为滚针的接触回复扭转半径随时间变化的函数。

滚针刚进入承载区时的回转半径最大，使得扭转回转力矩为最大，即为

Mnfmax=Febrn=μKμQψebln。

(7)

回复力矩随时间逐渐减小到零，滚针最终也回到自身轴线平行于轴承轴线的位置。

3.3 歪斜滚针回复过程的运动分析

由于内、外滚道的约束作用，滚针的歪斜是有限的，当进入承载区后，滚针承受径向力、轴向力的同时,还要承受回转力矩的作用；滚针受到滚道的约束作用力，最终回复与滚道的正常接触，其歪斜角α也逐渐接近于零。

假设滚针匀速的进入承载区，在滚针歪斜的条件下，其接触长度Lg为

(8)

式中：0≤t≤tg；ωe为轴承外圈角速度；tg为滚针回复所需的时间；ln为滚针的长度；E为外滚道直径；Dw为滚针直径。

由(8)式可得，随着滚针回复过程的进行，滚针与滚道的接触长度逐渐增加，直至全滚针长度正常接触。

3.4 歪斜滚针回复过程中的轴向摩擦力分析

在回复摩擦力矩的作用下，歪斜滚针在tg时间内回到与轴承轴线平行的正确轨道上，此过程滚针从α角回复到正常状态(不存在歪斜角)，滚针的轴向力也从最大减小到接近于零。同时，由于滚针脱离保持架的推力作用，此期间轴向力为

Fxn=(Febcosβ+Fef+Fif+Qψebsinβ)cosα+(Qψef+Qψebcosβ-Qψif-Febsinβ)·sinα。

(9)

由于β很小，可以设进入承载区的滚针的径向载荷不变，即Qψ不变，则轴向力的变化由歪斜角的变化引起，根据以上分析，可得轴向力Fxn(t)为

(10)

由(10)式可得，轴向作用力与歪斜角有较大关系，α角越大，Fxn越大，对轴承偏移有决定性作用。回复时间tg与外圈的转速成反比，外圈转速越大，则tg越小，轴向摩擦力作用的时间也就越短，对减小偏移越有利，但是这种滚针的快速复位，必然会引起轴承的振动与噪声。轴向作用力还与进入承载区时滚针的径向载荷正相关。轴承游隙越大，则承载的滚针数量相对越少，承载区滚针的径向载荷越大，因此，减小轴承游隙可以减小外圈的偏移量。

4 歪斜滚针接触应力

滚针歪斜后,在平行于轴承轴线的截面上截得的滚针截面为椭圆, 其长轴在轴承轴线方向,大小与滚针歪斜角有关，短轴在滚针的直径方向。滚道的约束作用使得滚针向减小歪斜的趋势运动，直至歪斜角为零。

对于理想的滚针轴承接触，每个滚针承受的载荷为[6-7]

(11)

式中：ψ为滚针的位置角；ε为载荷分布系数；Qmax为滚针的最大法向载荷。

在歪斜状态下，滚针与滚道之间为点接触(2个椭圆相接触)。根据Hertz点接触理论，歪斜滚针与滚道之间的接触变形区域为一个椭圆形区域[8-9]，则可得在Qψ力作用下，歪斜滚针与滚道间的弹性接触变形量δψ为

(12)

式中：K(e)为接触椭圆的积分系数；∑ρ为主曲率之和；E′为滚针材料当量弹性模量；ma为接触椭圆归一化的长半轴系数；E1，E2分别为滚道、滚针的弹性模量；μ1，μ2分别为滚道、滚针的泊松比。

滚针与滚道的接触长度即为接触椭圆的长半轴a

(13)

在进入承载区的过程中，滚针与滚道的接触情况从点接触开始，到线接触结束，其接触应力从点接触的最大到线接触的最小，如图5所示。因为从点接触到线接触是一个逐渐过渡的过程，接触应力的计算可以类比点接触的模型来表示。根据(12)式可得滚针与内、外滚道之间的接触变形量δψi，δψe分别为

图5 滚针在进入承载区过程中接触长度及接触应力的变化

(14)

(15)

式中：∑ρi，∑ρe分别为滚针与内、外滚道接触点的主曲率和。

由(13)式可知，接触椭圆的长半轴a与轴承接触副的接触半径以及载荷有关，假设载荷不发生变化，滚道接触长度发生变化会使接触应力发生变化。

由(14)～(15)式可知，由于轴承内、外滚道的曲率半径不同，在径向载荷(滚针法向力)的作用下，其与滚针的接触变形也不相同，相对而言，由于轴承内滚道的曲率半径小于外滚道的曲率半径，因而滚针与内滚道间的接触变形量大于滚针与外滚道间的变形量。

由图5可知，滚针偏斜角越大，则滚针进入滚道初始阶段的接触变形越大，越易使滚针的两端偏磨。

由以上分析可知，歪斜滚针进入承载区的起始阶段，滚针与滚道处于点接触状态，接触应力较大，极易造成疲劳损坏；在此过程中，其由于承受弯曲应力的循环作用，也极易发生折断。

5 结论

(1)保持架引导面误差会使滚针在进入轴承承载区的过程中处于歪斜状态，滚针歪斜将产生轴向摩擦力，使轴承产生轴向偏移，极大地影响轴承的接触质量。

(2)滚针歪斜工况下,滚针与滚道间为点接触，滚针与内圈间的接触应力最大，极大地影响滚针轴承的接触强度。

(3)滚针进入滚道过程中,滚道有修正滚针歪斜的作用，外圈会对歪斜滚针施加回复力，使其在进入承载区的过程中回复到理想正常状态。