基于量子遗传算法的水下图像增强

饶星星，盛惠兴，李佳佳

(河海大学计算机与信息学院，常州 213022)

1 引言

图像增强是把原来模糊不清晰的图像变得清晰，或者抑制图像的某些特征而使另外一些特征得到增强。其主要目的是使处理后的图像质量得到改善，增加图像的信噪比，增强图像的视觉效果。由于水下图像对比度低，识别度不高且边缘和纹理模糊不清，因此需要寻找一种有效的增强方法。传统的图像增强方法对水下模糊图像的增强效果不是很明显，基于上述特点，提出了一种基于量子遗传的算法，实现在小波域中对水下图像进行非线性增强。

2 常用图像增强算法

常用的图像增强方法大致可以分为空域法和频域法两大类。空域法是直接对图像的像素进行处理，主要方法有直方图均衡化和灰度级映射变换［1］;而频域法则是在某个变换域(如傅里叶变换、DCT 变换)内进行，处理的是变换后的系数，需要对处理后的变换系数进行反变换，才能得到增强的图像。在变换域下通常采用低通滤波、高通滤波、带阻滤波等方法处理图像。除此之外，还有同态滤波增强、自适应迭代滤波增强以及伪彩色和假彩色等许多增强方法。目前使用最多的增强算法还是直方图均衡化法、灰度级映射变换法和频域图像增强。在频域增强中主要有低频滤波和高频滤波，而常用的频域低通滤波器有理想低通滤波器、巴特沃斯低通滤波器和指数低通滤波器［2］;常用的高通滤波器有理想高通滤波器、巴特沃斯高通滤波器和指数高通滤波器。

3 量子遗传算法的图像小波域自适应非线性增强

3.1 遗传算法基本原理

遗传算法是一类仿生型的优化算法，它以达尔文的生物进化论和孟德尔的遗传变异理论为基础，利用简单的编码技术来模拟生物进化的优胜劣汰规则和染色体的交换机制，是一种自适应概率性的搜索算法。它可以在人工系统中实现特定目标的优化而不依赖于问题本身的特征，具有高级鲁棒性和广泛适应性，为解决许多传统算法难以解决的复杂问题和非线性问题提供了崭新的途径。

遗传算法的基本思想是从一组随机产生的初始解(“种群”)中开始进行搜索，种群中的每一个个体，即问题的一个解，被称为“染色体”。染色体的优劣是用“适应度”来评价的，适应度高的染色体被选择的概率高。被选择的染色体进入下一代，同时对下一代的染色体进行交叉和变异等操作从而产生新的后代，这样一直进行下去，直到算法收敛，这时的染色体就是最好的染色体，即是问题的最优解［3］。然而它的局限性在于其算法编码不能全面地表述优化约束，在解决一些复杂问题时容易陷入局部最优、早熟收敛和收敛速度慢的缺陷。

3.2 量子遗传算法基本原理

近几年新发展起来的量子遗传算法是量子计算和遗传算法相结合的产物，它用量子位编码来表示染色体，种族规模小而不影响算法性能，使得一个染色体可以表达多个模态的叠加，增加了种群的多样性，使全局达到最优的能力更强。它采用量子旋转门来对染色体进行更新和搜索，加快了算法的收敛，且可以避免早熟现象。

在量子遗传算法中，基因是用量子位存储和表示的:

式中，(α，β)都是常数，且满足:|α|2+|β|2=1。其中，|0〉表示自旋向下态，|1〉表示自旋向上态。即一个量子位不再是表达某一个确定的信息，它可能是0 态，也可能是1 态，也可能是它们的任意叠加态，即可以包含所有可能的信息。因此，对这个量子位进行任意操作会影响到所有可能的信息。

1个包含有m个基因的染色体可以具体定义为:

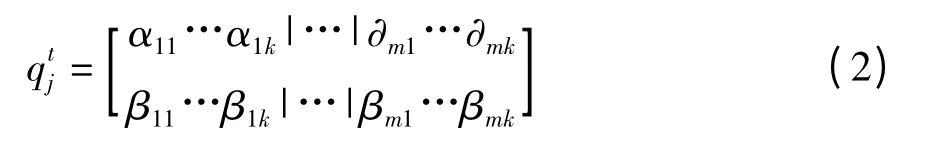
量子遗传算法通过构造量子旋转门作用于量子态叠加，使其相互干扰，改变旋转角度，更新种群，从而代替了传统遗传算法中的选择、交叉、变异等操作方法。常用的量子旋转门为:

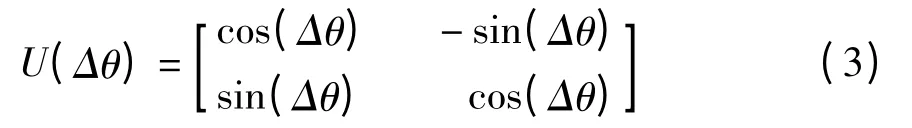
量子遗传算法的流程图见图1 所示。

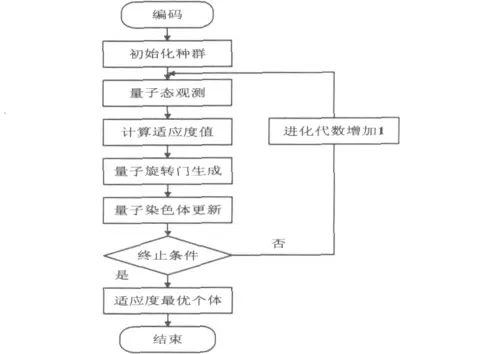
图1 量子遗传算法流程图

3.3 利用量子遗传算法实现图像小波域自适应非线性增强

为了在增强水下图像细节的同时去除残留的噪声，提高对比度，分别选用了两种非线性增益函数对分解出来的小波低频系数和小波高频系数进行处理。

因为低频系数反应的是图像的基本信息，是整个图像对比度的体现，因此对低频系数采用归一化的非完全Beta 函数进行非线性增强。非完全Beta函数是F(u)，表达式为:

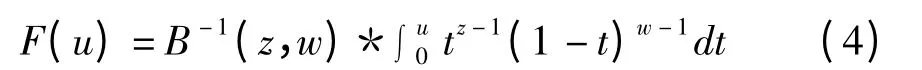
图像经小波变换后高频系数主要反应的是图像的细节信息，而噪声又主要集中在高频方向子带中。所以对于高频方向子带系数采用阈值法进行处理，抑制较小的系数，保持较大的系数，放大绝对值介于中间的系数。这里阈值由最细子带的水平方向分量的方差估计得到［4］。

通常，对低频系数处理所采用的非线性函数中的两个参数z 和w 值比较难以确定，一般采用人工干预的方法或穷举法，这种方法比较耗时，并且没有智能性。针对人工方法或穷举法的弊端，采用了一种量子遗传算法。该算法首先根据水下图像的特点自动找出对低频进行处理的非线性函数中最优的z，w 值，然后在小波域内用两个非线性函数分别对低频系数和高频系数进行处理，最后反变换得到增强后的图像。

3.4 小波域自适应非线性增强算法步骤

(1)统计图像的灰度级分布范围及其分布情况，分别用f(x，y)和f'(x，y)表示输入图像和输出图像的灰度值，对输入图像的灰度值进行归一化处理:

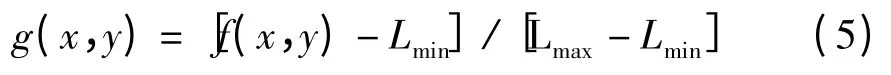
其中，Lmax和Lmin分别表示输入图像灰度的最大值和最小值，0≤g(x，y)≤1。

(2)利用量子遗传算法将输出图像和输入图像的对应关系进行编码，产生一组随机对应关系即初始群体。每条染色体中包含两个基因段，分别为z和w。根据式(4)，每个个体都对应一个非线性变换函数F(u)，0≤u≤1。在小波域内用式(4)中的非线性变换函数对低频系数进行处理，然后进行反变换得到处理后的图像，处理后的图像所对应的灰度值为g'(x，y)，则对应关系可以表示为:

其中，0≤g'(x，y)≤1。

根据g'(x，y)的值可以得到输出图像f'(x，y):

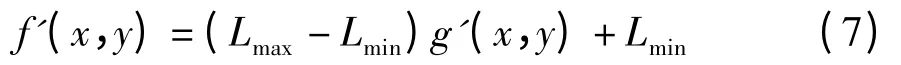
(3)采用对比度测量函数作为量子遗传算法的适应度函数，表达式为:

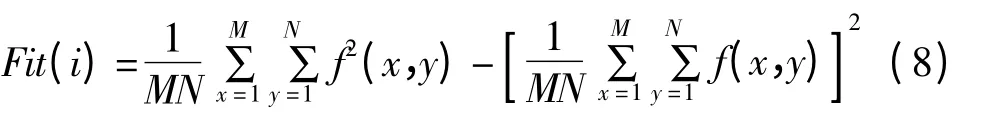
其中，M，N 分别为图像的行数和列数，f 代表增强后的图像，i 表示染色体。对比度测量函数反映了图像灰度分布的均匀性，该值越大，代表图像灰度的分布越均匀，对比度越高，图像的视觉效果越好。

(4)选择适应度值最大的个体作为当前代的最优个体，利用量子旋转门对其它个体进行更新，得到新的群体，重复上述操作，不断生成新的灰度对应关系组，直到满足规定好的优化准则。在所有的进化代中找到最优或者近似最优的灰度变换关系，从而得到非线性变换函数中最优的z 和w 值。

(5)对输入图像进行四层小波分解，根据得到的z 和w 值所组成的非完全Beta 函数对分解得到的低频系数进行处理，然后再用一组非线性函数对小波分解后的高频系数进行增强处理［5］。

(6)对小波系数进行重构，得到增强后的图像。

4 实验结果与分析

为了验证本算法的有效性，现对一组从水下视频中截取的图像采用该改进算法进行增强处理，并将结果同直方图均衡化以及灰度级非线性拉伸算法的结果进行对比。为了说明该改进算法的优越性，实验中给出各个图像的直方图，便于分析各种方法增强后的对比度。

三种算法的增强效果如图2 所示，其中，图2(a)为从水电站拦污栅视频中截取的原图;图2(b)为采用直方图均衡化处理的结果;图2(c)为采用Beta 函数进行灰度非线性拉伸的结果;图2(d)为改进算法的结果。图3 中的图3(a)～图3(d)为三种方法对应的直方图。

图2 水电站拦污栅图像三种增强效果对比

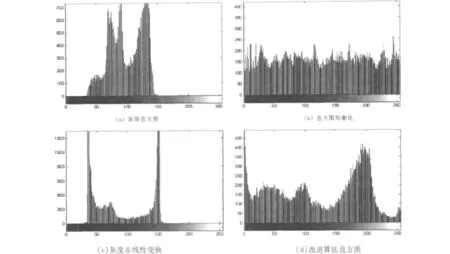
图3 各种方法增强后直方图

从图2 中可以看出图2(a)的对比度很低，拦污栅的纹理和边缘都模糊不清;图2(b)经过直方图均衡化后，图像的对比度得到了较好的拉伸，但是局部出现了过度增强的现象，如第2 条栅栏的中间部分及第一条栅栏的右半部分都出现过度增强;图2(c)为经过非完全Beta 函数灰度级非线性拉伸的结果，效果不是很理想，对比度只得到了略微改善，纹理和细节依旧无法突出;而从使用改进后的算法处理过的图像(图2(d)所示)可以看到，不仅对比度得到了改善，而且边缘和细节也得到了较好的增强，如第一条栅栏的边缘及其上面的铁锈明显比直方图均衡化的结果看起来清晰。从直方图上看，原图像各像素点的值分布比较集中，而经过改进算法处理过的图像像素点在整个灰度范围上得到了很好的分布。

5 结束语

为了提高水下图像的对比度，突出纹理和边缘细节信息，将基于量子遗传算法的小波域自适应非线性增强方法应用到水下图像增强中。实验结果表明，对于图像模糊，对比度较低的水下模糊图像，传统的直方图均衡化以及灰度级拉伸算法的效果在对比度上有所提高，但会出现过度增强的现象。而改进算法对水下模糊图像的增强表现出了较好的效果，不仅使图像的对比度得到了拉伸，而且突出了图像的边缘和纹理等细节信息，使其视觉效果得到了明显改善。

［1］张强，王正林.精通MATLAB 图像处理［M］.北京:电子工业出版社，2009.

［2］高赟.图像灰度增强算法的研究［D］.西安:西安电子科技大学，2007.

［3］张丽丽.基于遗传算法的区域水资源系统多目标优化方法研究［D］.辽宁:辽宁工程技术大学，2005.

［4］田晓东，刘忠.基于自适应迭代阈值的声纳图像增强算法［J］.舰船电子工程，2006，152(2):154－157.

［5］M Elad，A Feuer.Super_resolution restoration of an image sequence:adaptive filtering approach［J］.Digital Object Identifier，1999，8(3):387－395.