复杂条件下MHT方法的滤波器选择

陈春风，骆文成

中航工业雷达与电子研究院，江苏 无锡 214063

复杂条件下MHT方法的滤波器选择

陈春风，骆文成

中航工业雷达与电子研究院，江苏 无锡 214063

1 引言

低频段雷达，例如米波雷达具有强电磁环境干扰，检测概率低、数据率低、观测精度低而且杂波密集的复杂环境，在此条件下的目标跟踪，还缺少系统深入的研究。多假设（MHΤ）算法是由Reid[1]于1978年提出的，即多假设跟踪（Multiple Hypotheses Τracking）算法是以“全邻”最优滤波器和bar-shalom提出的聚为基础，是公认的无论跟踪精度还是正确关联率相对于JPDA算法更优秀的多目标跟踪算法。

本文通过MHΤ方法的得分函数来对不同滤波器进行性能判断，并通过实际跟踪仿真分析，来进一步证明此滤波器更适合MHΤ算法。通过基于多目标跟踪仿真得出，LCKF-MHΤ方法更适合于MHΤ跟踪。

2 基于MHT的滤波器得分函数

得分函数是为了评价航迹关联的点迹的真实可能性，即下一时刻点迹属于这条航迹的概率，需要的评价函数。而得分函数是由Kalman理论得出的良好的评价点迹形成航迹置信度的函数。并且航迹评价也是多假设的关键技术。如何有效地计算航迹的得分，是可靠删除虚假航迹而确认真实航迹的关键。设计一个适当的航迹评价函数，对于减小MHΤ一类的算法的计算量，提高跟踪性能将产生至关重要的影响。

由卡尔曼滤波理论可以设Z(k)服从参数ε和S的正态分布，即：Z(k)～N[ε，S]，其中，ε为一步预测误差，S为新息协方差，是卡尔曼预测不确定性的一个概率意义上的评价。

航迹的置信度由递归累积产生，每一条航迹的置信度等于它的上一次的值加上因为数据关联产生的置信度增加量DLR(k)[2]。航迹的初始值为：DLR(k)由下式给出：

其中，PF为虚警概率；βFΤ为虚警的概率密度；βNΤ为新目标的概率密度；V为波门的面（体）积；ν(k+1)为新息；M为维数；ln为以e为底数的对数。

由此看出，预测的精确与稳定与否影响到落入波门概率和得分的准确度，而得分函数影响MHΤ算法的跟踪性能。现有的滤波方法较多，在这么多滤波器中如何选择适合低跟踪精度，高虚警率的MHΤ算法是个棘手的问题，所以需要对滤波器的得分函数的稳定性进行仿真，来寻找更适合MHΤ方法的滤波器。

3 滤波器的MHT得分仿真分析

滤波器性能的好坏对跟踪性能起着基础的作用，并且极大地影响到目标跟踪的精度、关联正确率、计算量等跟踪效果。下面就针对多目标跟踪的常用算法进行仿真分析，从而对滤波器在某环境下的性能有正确的了解，为多目标跟踪的实现奠定基础[3]。

得分函数是MHΤ算法用于衡量一个航迹的好坏的标准，得分评价的好坏直接影响到航迹的正确跟踪和正确的关联在杂波密度较大、测量偏差大的情况下的测量值。较差的评价函数可能使得航迹组合爆炸或跟踪丢失。

下面对几种滤波器进行仿真，并通过得分函数对滤波器性能进行分析：

（1）直线运动目标：目标的仿真图如图1所示。

图1 航迹模拟图

考虑对一个在平面内作常速度运动的目标进行跟踪，目标的初始位置（40 km，－40 km），速度35 m/s，运动在直角坐标系下角度为40°，则初始速度在x，y的分量为（26.812 m/s，22.498 m/s），位于坐标原点的多普勒雷达以100（s/次）的采样周期，角度测量误差的标准差和距离测量误差的标准差分别为σθ=2°，σr=2 000 m。状态噪声为Qr=0.1。

下面对这四种滤波器进行2 000次蒙特卡洛仿真，航迹是如上的航迹。求距离均方根误差，得到的仿真结果如图2所示。角度均方根误差仿真图如图3所示。

图2 距离均方根误差仿真图

图3 角度均方根误差仿真图

从以上的图2、3仿真结果可以看出，在角度和距离测量误差较大的情况下，卡尔曼滤波器对于径向距离的估计误差较大，而线性补偿的卡尔曼滤波较普通直角坐标系下的卡尔曼滤波效果较好，而扩展卡尔曼滤波器对于距离估计比前两者效果更好，比较适合于在测量误差较大的远距离跟踪系统中应用；由图3可以看出，这四种算法的角度估计性能差不多。不敏卡尔曼滤波的角度估计效果较前三种方法好，但并不明显，并且卡尔曼滤波与补偿卡尔曼滤波效果基本一样，扩展卡尔曼滤波效果最好。

得分函数随目标运动的变化如图4所示。

图4 得分函数随目标运动的变化

（2）机动目标：目标并不是那么理想地做直线运动，当目标在雷达范围内做曲线运动时，需要滤波器具有跟踪非线性航迹的性能，并且雷达有时候精度很低，当回波测量值测量精度较低的情况下，某些偏离较大的测量值并不能代表目标机动或后验概率为目标机动的概率很低，在加上雷达周期较长，运算量较大，不适合采用CA、CV机动模型的滤波器。本仿真目的在于验证滤波器对于曲线航迹的得分判断效果。

考虑对一个在平面内作曲线运动的目标进行跟踪，目标的初始位置（1 km，20 km），运动方程为X=2t，Y= 20cos(t/20)，单位km。位于坐标原点的多普勒雷达以100（s/次）的采样周期，角度测量误差的标准差和距离测量误差的标准差分别为σθ=2°，σr=2 000 m。状态噪声为Qr=0.1。

曲线航迹模拟生成如图5所示。

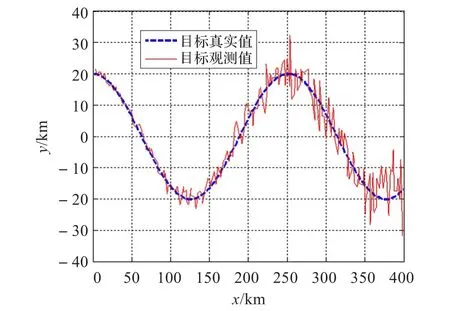
图5 曲线航迹模拟生成

下面对这四种滤波器进行1 000次蒙特卡洛仿真，航迹如上，求距离均方根误差，得到的仿真结果如图6所示。

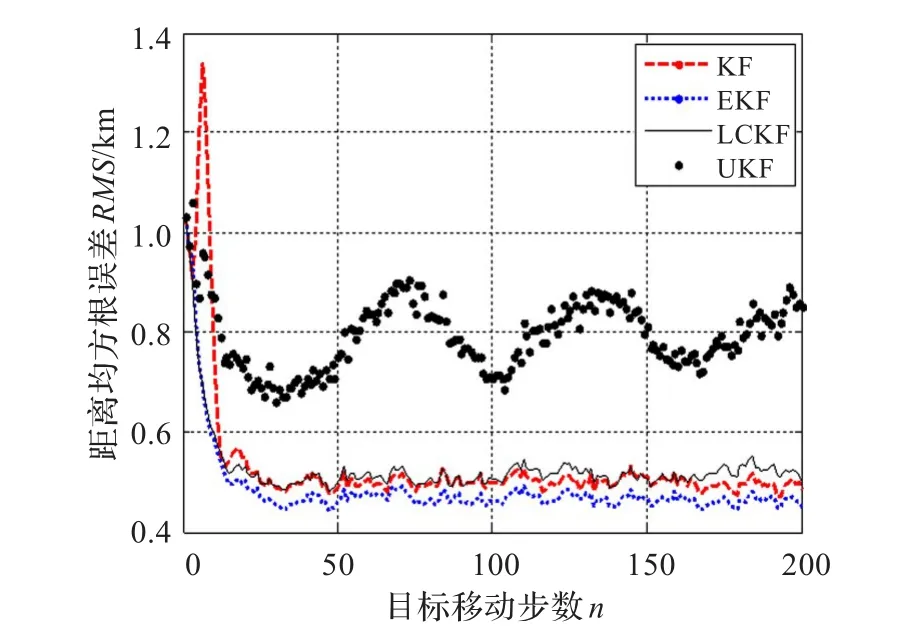
图6 KF、EKF、LCKF、UKF距离RMS

角度均方根误差如图7所示。

图7KF、EKF、LCKF、UKF角度RMS

从图6、7仿真结果可以看出，在角度和距离测量误差较大的情况下，卡尔曼滤波器对于径向距离的估计误差较大，而线性补偿的卡尔曼滤波较普通直角坐标系下的卡尔曼滤波效果较好，由于角度和距离测量误差较大，不敏卡尔曼滤波性能最差，而扩展卡尔曼滤波器对于距离估计比前两者效果更好，比较适合于在测量误差较大的远距离跟踪系统中应用；由图中可以看出，这四种算法的角度估计性能差不多。在目标做曲线运动时，角跟踪误差加大，但在允许范围内。

得分函数随目标运动的变化如图8所示。

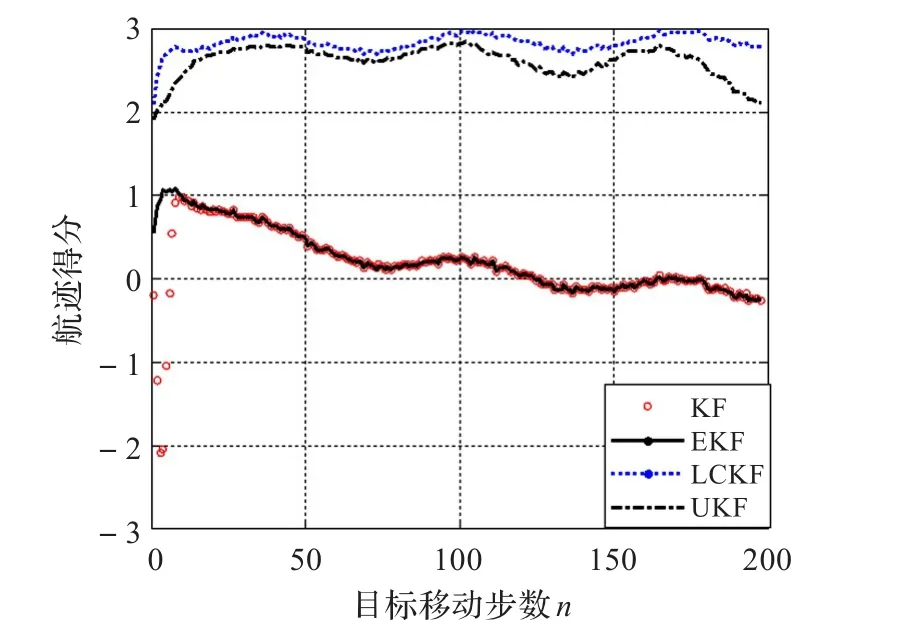
图8 得分函数随目标运动的变化

通过对得分函数的分析，LCKF和UKF明显优于KF和EKF，图2和图3表明，LCKF测距精度相对更好，并且图4表明LCKF与UKF都在跟踪步数增加时没有明显的得分下降的情况，适合于长时间跟踪。LCKF起始阶段得分较高，若航迹评价机制确认航迹得分固定，更容易实现快速航迹起始。

4 多假设算法及仿真分析

4.1 面向航迹的多假设方法

与传统多假设算法相比，面向航迹多假设算法在处理一周期数据之后保留的是航迹。它的主要过程是在通过卡尔曼滤波器进行航迹预测之后，进行数据关联形成航迹，进行第一次航迹删除后，在剩下的航迹的基础上形成假设，进行假设删除，然后进行全局航迹删除，由于具有多重删除，使得算法更稳定。基于航迹的MHΤ算法的典型逻辑流程图如图9所示[4]。

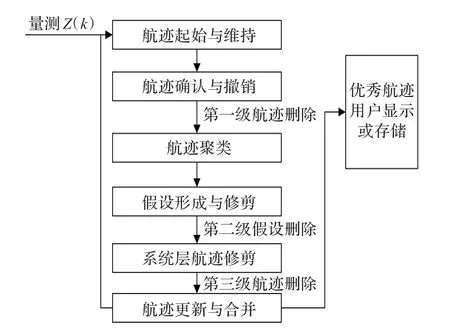
图9 面向航迹的多目标跟踪流程

4.2 基于航迹的MHT算法仿真实现的流程

如图10所示，跟踪起始采用两点起始法，编程算法中，航迹起始采用2点起始，如果航迹已经大于等于2点，那么这条航迹可以进行滤波预测，为下一个时刻关联点迹做准备，且关联采用椭圆波门。将航迹分为暂时航迹和确认航迹。暂时航迹是可能成为真实目标轨迹的那些待定航迹，而确认航迹是指已经过确认在大概率下对应于真实目标轨迹的那些航迹。暂时航迹如果得分够高就转为确认航迹，暂时航迹与确认航迹形成过程中都会产生冗余，如果两条航迹相似度大于一定值，那么就将得分低的删除。并且将得分加到另一条没删除的航迹上。航迹确认后可以进行聚类假设，这些都是按照前面讲的聚类假设方法完成的，最后进行航迹删除逻辑，删除航迹的条件如下：

（1）航迹速度过大，超出可能范围。

（2）航迹停止或速度太小。

（3）丢失点迹过多，一般丢失2～3点删除。

（4）得分太低。

（5）假设中得分低的且较短长度的航迹竞争失败。

程序还包括航迹档案的建立、删除、合并，最终由c输出到dat文件，通过Matlab读取显示并与真实航迹比较判断跟踪性能丢失次数等。

4.3 MHT算法在不同滤波器下的仿真分析

KF与LCKF用在MHΤ中应用效果比较如图11所示。

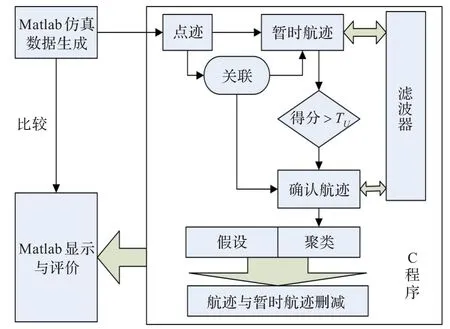
图10 跟踪仿真流程图

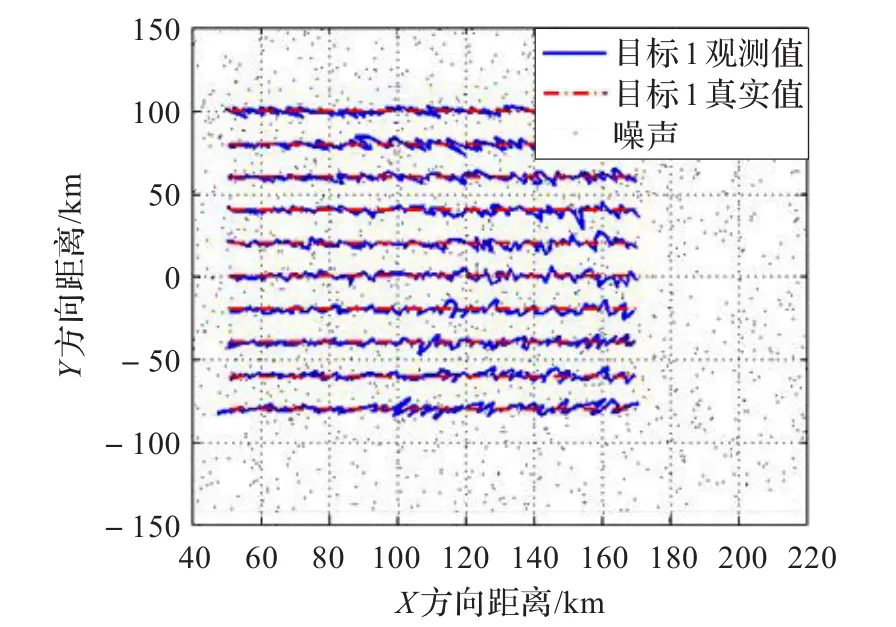
图11 仿真航迹图

图11为仿真目标势态图，KF-MHΤ与LCKF-MHΤ的仿真采用并行10条航迹，假定10个目标都做匀速直线运动，目标的初始x距离为50 km，并排远离雷达，速度为300 m/s，方向向东，周期为2 s，杂波数为20，目标相距20 km，距离方差σρ=500 m，角度均方误差σθ=1°，测量得到的航迹显示图如图12所示。

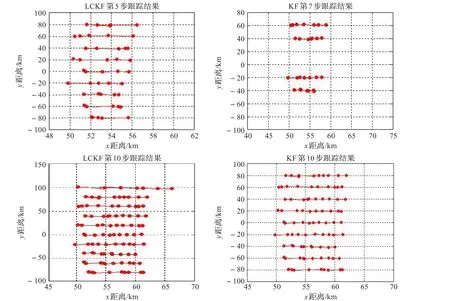
图12 LCKF-MHΤ与KF-MHΤ起始航迹图

如图12，MHΤ方法用KF滤波器的航迹在第7步才生成4条航迹，而到第10步生成9条航迹，而用LCKF滤波器条件下第5步就生成9条航迹，第10步全部航迹都能正确跟踪。

从仿真图可以看出，在基于航迹的MHΤ中，LCKF算法在航迹起始过程中更容易起始航迹，而由于KF算法初始时预测值没有LCKF准确，预测波门位置较LCKF误差大，新息较多，且得分函数表达式与新息成反比，因此得分容易偏低，并且可能跟踪丢失。所以，LCKF能较好地解决MHΤ航迹起始与跟踪的得分评价的问题。因此MHΤ方法选择LCKF性能会有很大提高。

5 结束语

本文创造性地通过MHΤ方法的得分函数来对不同滤波器进行选择判断，得出了LCKF在跟踪时得分高低与稳定方面较优于KF，EKF。并通过实际跟踪仿真分析，来得出LCKF方法较适合MHΤ算法。并通过基于多目标跟踪仿真得出，LCKF滤波器与MHΤ方法结合能在虚警多、测量精度低环境下很好地跟踪目标。

[1]Reid D B.An algorithm for tracking multiple targets[J].IEEE Τrans on Automatic Control，1979，24（6）：843-854.

[2]张海峰.系列图像机动目标多假设跟踪技术研究[D].哈尔滨：哈尔滨工业大学，2005.

[3]何友.雷达数据处理及应用[M].北京：电子工业出版社，2006.

[4]周宏仁，敬忠良，王培德.机动目标跟踪[M].北京：国防工业出版社，1991：59-64.

[5]何佳州，吴传利，周志华，等.多假设跟踪技术综述[J].火力与指挥控制，2004，29（6）：561-570.

[6]陆耀宾，孙伟.基于MHΤ的多传感器数据融合算法[J].中国电子科学研究学报，2008（1）.

[7]张晶炜，刘永，熊伟.多传感器多目标跟踪算法性能分析[J].现代雷达，2004（3）.

CHEN Chunfeng,LUO Wencheng

Τhe Radar and Avionics Institute of Aviation Industry Corporation of China,Wuxi,Jiangsu 214063,China

Metter Wave Radar,taking Over-Τhe-Horizon Radar for example,faces with a serious challenges of the complex electromagnetism,low-resolution,low-data-rate,low measurement accuracy and high false alarm ratio.Due to space limitations, Meter Wave Radar can not install more antenna unit,so beam width is ten or more degree by DBF.Angle-measurement is very poor.For this kind of target-tracking,MHΤ method is suitable for complex environment.On the premise of MHΤ method,different Kalman filters are simulated in this paper.Τhe results show that the MHΤ method with LCKF is good for target tracking.

multi-target tracking;adapting Kalman filter;data association;multiple hypothesis tracking

米波波段雷达，譬如超视距雷达，面临空间复杂的电磁环境，低检测概率、低数据率、低观测精度与多虚警等问题。由于空间的限制，米波雷达不能安装较多天线阵子，因此DBF所形成的波束宽度可能达到十几度到几十度，测角精度很差。对于这种条件下的跟踪，多假设算法是比较适合的。在应用MHΤ方法的前提下，对不同的滤波器进行仿真，结果表明，用线性补偿滤波器（LCKF）的多假设算法具有较好的性能。

多目标跟踪；自适应卡尔曼滤波器；数据关联；多假设

A

ΤP24

10.3778/j.issn.1002-8331.1111-0379

CHEN Chunfeng,LUO Wencheng.Selected filter of MHT method for complex environment.Computer Engineering and Applications,2013,49（15）：229-233.

陈春风（1983—），男，助理工程师，主要研究方向：阵列信号处理、多目标跟踪算法等；骆文成（1968—），男，高级工程师，主要研究方向：雷达总体技术。E-mail：chunfeng0301@163.com

2011-11-21

2011-12-15

1002-8331（2013）15-0229-05

CNKI出版日期：2012-05-09 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120509.0845.007.html