新阈值函数下的小波阈值去噪

王 瑞，张友纯

中国地质大学（武汉）机械与电子信息学院，武汉 430074

新阈值函数下的小波阈值去噪

王 瑞，张友纯

中国地质大学（武汉）机械与电子信息学院，武汉 430074

1 引言

现实环境中，由于噪声的存在，语音信号会不可避免地受到干扰，严重时甚至会被噪声淹没。语音去噪一直是语音信号处理中的热点，它的目的是从被噪声污染的语音信号中尽可能多地提取出原始语音信号。小波变换发展于20世纪80年代末，它克服了短时傅里叶变换的缺点，可以对信号进行多尺度（多分辨率）的分析，特别适合分析像语音这样的非平稳信号[1]。目前小波去噪主要有三种方法：模极大值重构去噪法[2]、空域相关去噪法[3]和小波域阈值去噪法[4]。其中，小波域阈值去噪法由于计算量小，去噪效果好而被广泛研究和应用。

阈值的处理是小波阈值去噪的关键，Donoho提出了硬阈值法和软阈值法，但这两种方法都有自身的缺陷：硬阈值法连续性差，重构可能会产生震荡；软阈值法虽连续性好，但估计值和实际值之间总存在恒定偏差，会给重构信号带来一定的误差。因此，寻找新的阈值处理方法是小波域阈值去噪的热点研究方向[5]。

本文提出了一种新的阈值函数，来克服传统小波阈值去噪法的上述缺点，提高语音信号的信噪比。实验证明，本文提出的新的阈值函数与传统的阈值函数，如硬阈值函数，软阈值函数和折衷阈值函数相比，能更明显地改进语音去噪效果，提高语音去噪后的信噪比，可作为小波阈值去噪法的重要参考。

2 小波阈值去噪的原理

20世纪90年代初，小波去噪（de-noising）和降噪（noise reduction）的概念开始出现。1992年，Donoho和John Stone提出了小波域阈值滤波方法，它采用Mallat算法，大大减小了计算量，而且实现简单，去噪效果好，因而得到了深入的研究和广泛的应用。

一般的，含噪语音信号的模型可假定为：其中f(n)为真实语音信号，s(n)为含有噪声的语音信号，e(n)为噪声，σ是噪声强度，N为离散采样序列x(n)的长度。

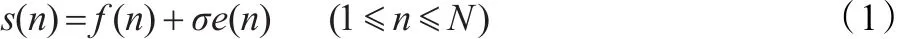
由于小波变换具有局部时频特性，在小波域中可以使信号的能量相对集中，而噪声信号的能量相对分散，表现为能量集中区域的信号的小波系数绝对值比较大，而分散区域的小波系数的绝对值小。通过设定一个合适的阈值，认为小于该阈值的小波系数由噪声产生而将其去除，大于该阈值的小波系数由信号产生而将其保留或收缩，从而达到信号和噪声的分离[6]。

小波域阈值去噪一般分为三个步骤：

（1）小波分解：选择合适的小波基和小波分解层数，对含有噪声的语音信号进行离散正交小波变换。

（2）阈值处理：在小波域对小波系数进行阈值处理。

（3）小波重构：利用处理后的小波系数进行小波重构。

小波阈值去噪的原理如图1所示。

图1 小波阈值去噪原理

2.1 阈值的确定

小波域阈值去噪法的关键在于阈值的选取[7]，如果阈值太小，去噪后的信号中仍会存在噪声；如果阈值太大，信号的有用部分又将被滤掉，从而引起失真。

常用的阈值确定规则有：固定阈值（sqtwolog规则），基于Stein无偏似然（SURE）估计（rigrsure规则），启发式阈值Τ3（heursure规则）和极值阈值Τ4（minimaxi规则）。在信号的高频分量小的情况下，无偏似然估计阈值和极值阈值不容易丢失信号中的有用成分，但固定阈值和启发式阈值可以更有效地去除噪声。

Donoho给出的固定阈值为：

其中，σ为噪声强度，N为信号的长度。由于语音信号的小波变换系数的模值随尺度的增大而增大，噪声的小波变换系数的模值随尺度的增大而减小，因而尺度增大时的语音成分就有可能被当做噪声处理了。因此，在固定阈值的基础上，本文采取修正的通用阈值[7]，表达式如下：

其中，γ为调整因子，当噪声为白噪声时，可取为1。j为小波尺度，Nj为第j层信号的长度。当j增大时，噪声的小波系数减小，阈值也减小，这样阈值就能根据不同的尺度进行调整。

2.2 阈值的处理

常用的阈值处理方法有硬阈值法和软阈值法两种方法，它们的表达式分别如式（4）和式（5）所示。

硬阈值法：

软阈值法：

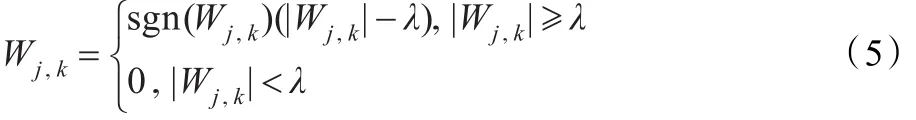
其中Wj，k为小波系数，λ为阈值。硬阈值法就是把信号分解后的小波系数的绝对值和阈值作比较，小于阈值的点变为0，大于或等于阈值的点保持不变。硬阈值法能够更多地保留真实信号中的尖峰特征，但在某些点不连续，会在重构语音信号时出现一定振荡。软阈值法连续性好，重建信号比较光滑，但处理后的信号的小波系数和原信号的小波系数间存在恒定的差值，这使得重构信号的信噪比较低，均方误差较大。

为了克服硬阈值和软阈值的缺陷，很多学者提出了新的阈值函数，最常用的有以下三种方式[8]：

（1）多项式插值法：为了克服硬阈值函数不连续和软阈值函数有偏差的缺点，采用以下多项式插值模型：

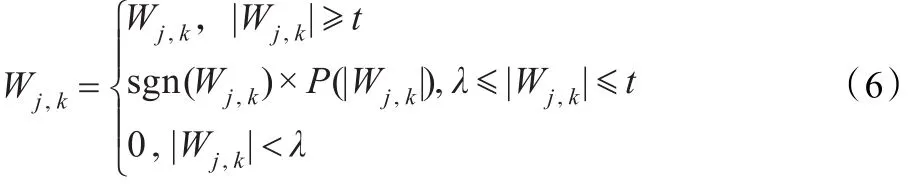
其中，P(|Wj，k|)称为插值多项式，通常可取为二次或三次多项式。多项式插值法得到的Wj，k在整个定义域内是连续的，当P(|Wj，k|)为三次多项式时，Wj，k在整个定义域内可导，因而易于处理，克服了硬阈值函数的不连续性。当|Wj，k|≥t时，Wj，k是无偏估计，也弥补了软阈值函数的不足。

（2）软、硬阈值函数折衷法：软、硬阈值函数折衷法表达式如下：

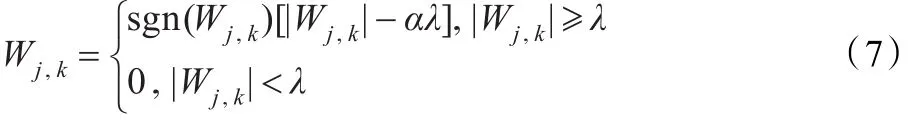
其中，0≤α≤1。当α分别取0和1时，上式即成为硬阈值函数和软阈值函数。该方法思路简单，去噪效果很好。

（3）模平方处理法：把|Wj，k|/λ看成一个整体，则软阈值函数可等效为：

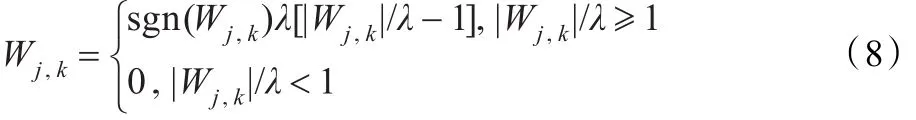
上式的含义为：当|Wj，k|/λ≥1时，Wj，k被认为主要是信号对应的小波系数，予以保留；否则，Wj，k被认为主要由噪声引起，应当消除。将|Wj，k|/λ进行平方处理，使得每一个系数与1的偏离程度增大，这样可以促进信号和噪声的分离，然后进行软阈值处理，最后开平方得到Wj，k。模平方处理法表达式如下：

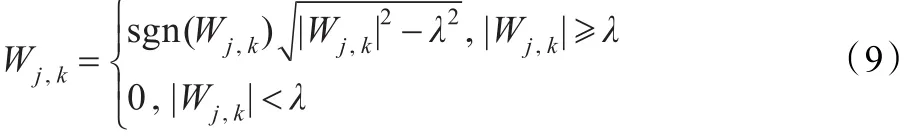
该方法估计出的值也介于软、硬阈值方法之间。

其他的阈值函数，如折衷非平滑函数阈值法，均方根非平滑阈值函数法，对数平滑函数法，指数平滑函数法，比值平滑阈值法和消去平滑阈值函数法等，都可看做上述三种阈值函数法的变形式。如指数平滑函数法[9]，就是将软、硬阈值函数折衷法中的α变为α=1-exp(-m(|Wj，k|-λ)2)，通过改变m来调整α的变化。

多数阈值函数在小波系数小于阈值(|Wj，k|＜λ)时，将小波系数(Wj，k)置为0，也即认为比阈值小的小波系数均为噪声产生。由于部分语音信号（如清音）[10]与噪声比较类似，如果直接将该部分置为0，将很有可能除去部分有用的语音信号。因此，结合折衷函数和μ律阈值函数，本文提出了一种新的阈值函数：

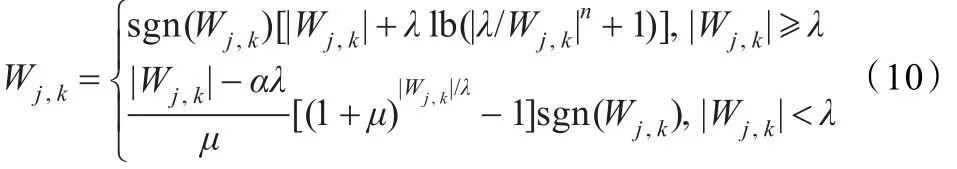
其中0≤α≤1。当|Wj，k|≥λ时类似于折衷函数，折衷因子为lb(|λ/Wj，k|n+1)，通过调节n来改变其大小。当|Wj，k|＜λ时，采用类似于μ律阈值函数[11]，通过改变α来对小波系数进行压缩。新的阈值函数克服了硬阈值函数和软阈值函数的缺点，保留了折衷函数和μ律阈值函数的优点。

3 新的小波阈值去噪算法

本文利用新的阈值函数进行小波阈值去噪，具体步骤为：首先，向纯净语音信号中添加高斯白噪声，然后选取合适的小波基，小波基阶数和小波分解层数进行小波变换。通过式（3）确定不同层次上的阈值，然后通过新的阈值函数（式（10））进行阈值处理。最后，用小波逆变换重构去噪后的信号。流程图如图2所示。

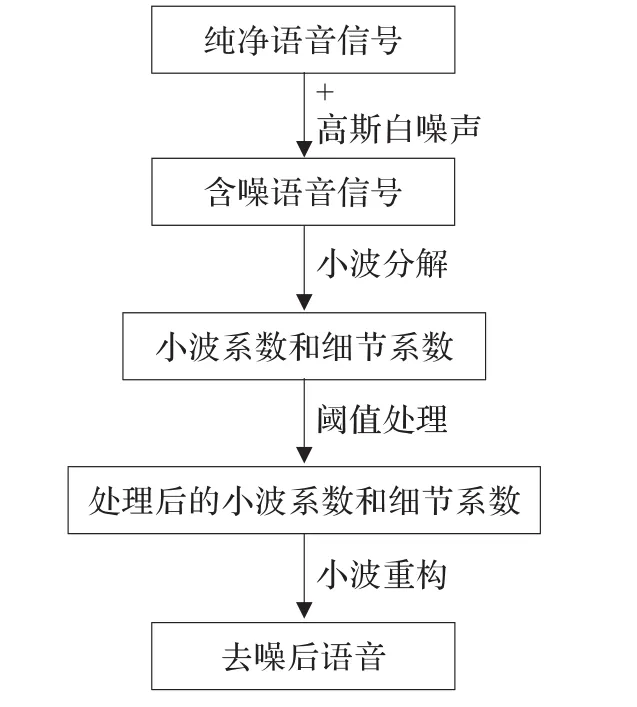
图2 小波阈值去噪

4 实验结果与分析

在语音信号处理中，信噪比（SNR）是最常用的一种衡量信号消噪有效性的指标，其公式为：

此外，去噪后的信号是否平滑，和原信号的接近程度也是消噪效果的标准之一。去噪后信号越平滑，毛刺越少，听起来与原信号越接近，则去噪效果越好。

在Matlab环境下，分别进行了最优小波基的选择实验，新阈值函数最优参数的选择实验以及新阈值函数与硬阈值函数，软阈值函数和折衷函数的比较实验。小波分解尺度越大，低频部分被分解的次数也就越多，去除噪声的效果也要好一些，但是计算量会增大。综合考虑，实验中选择小波分解层数为4。通过实验可以看出，新的阈值函数相比硬阈值函数，软阈值函数和折衷阈值函数，都有明显优势，从而证明了本阈值函数的有效性和可行性。

4.1 最优小波基的选择

不同的小波基函数有不同的性质，如对称性，消失矩等[12]。由于这些不同的性质，使得不同的小波基在时域和频域上表征信号局部特点的能力不同。表征信号局部特点的能力越强，越有利于检测信号的瞬态或奇异点。而对于某种特定的小波基，阶数不同，表征信号局部特点的能力也不同。一般情况下，阶数越高表征信号局部特点的能力就越强，但是计算量也会相应变大。

在输入信噪比为5 dB，α=0，n=1 000时，分别利用Daubechies小波族、Symlets小波族和Coiflet小波族进行了四层小波变换，然后进行阈值去噪处理，选取去噪效果最好的最优小波基。

由表1可以看出，在相同的条件下，coif族小波的去噪效果优于db族小波和sym族小波。db族小波和sym族小波的去噪效果差别不大，N=1，2，3时，它们的输出信噪比完全一致。随着N的增大，db族，sym族和coif族的小波去噪后的信噪比都增大。因此，在本实验中，选择coif5作为最优小波基。

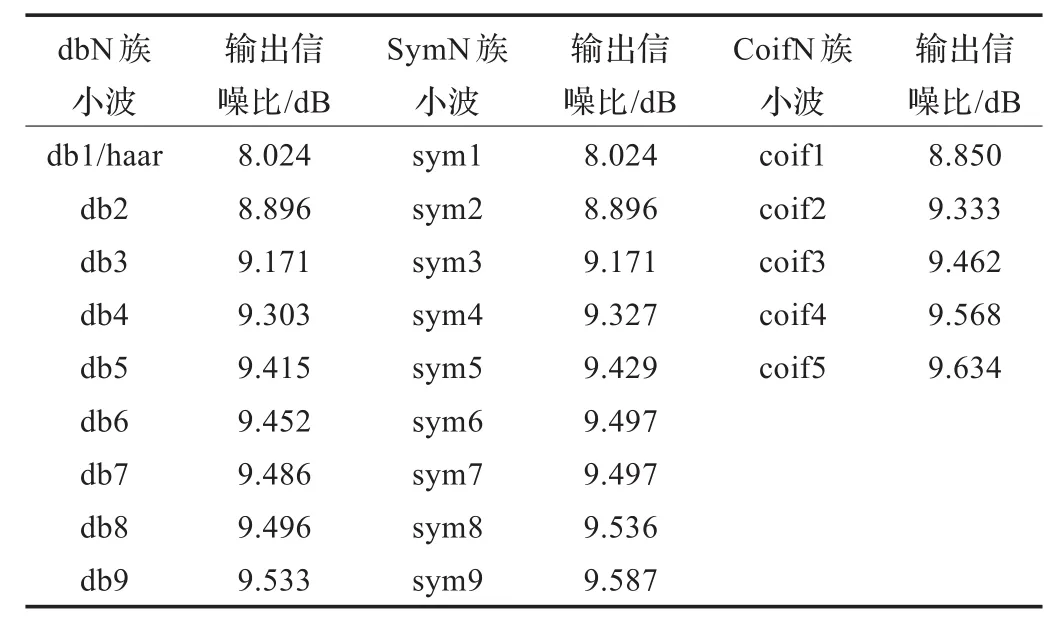
表1 最优小波基的选择

4.2 新阈值函数的最优参数的选择

在μ=255，输入信噪比SNR=5 dB时，采用“coif5”小波进行4层小波分解，选择阈值函数（式（5））的最优参数α和n，结果如表2所示。

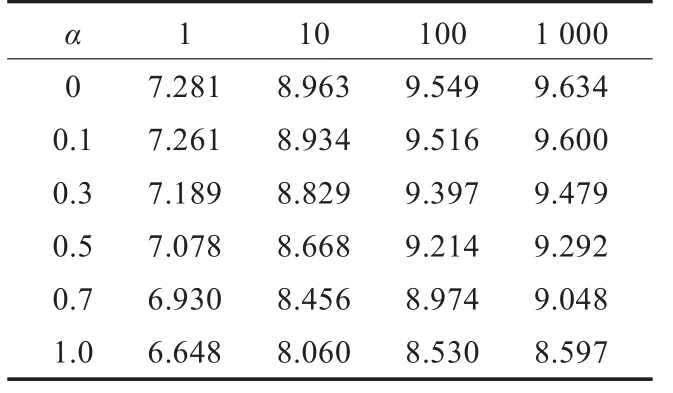
表2 最优参数的选择

通过结果可以发现，α越小，n越大，去噪效果越好。n越大，计算量也会越大，而信噪比提高变得缓慢，因此，实践中n取1 000以内比较合适。

在输入信噪比为5 dB，α=0，n=1 000时，新阈值函数去噪后语音信号与原始语音信号，含噪语音信号的对比如图3，图4所示。

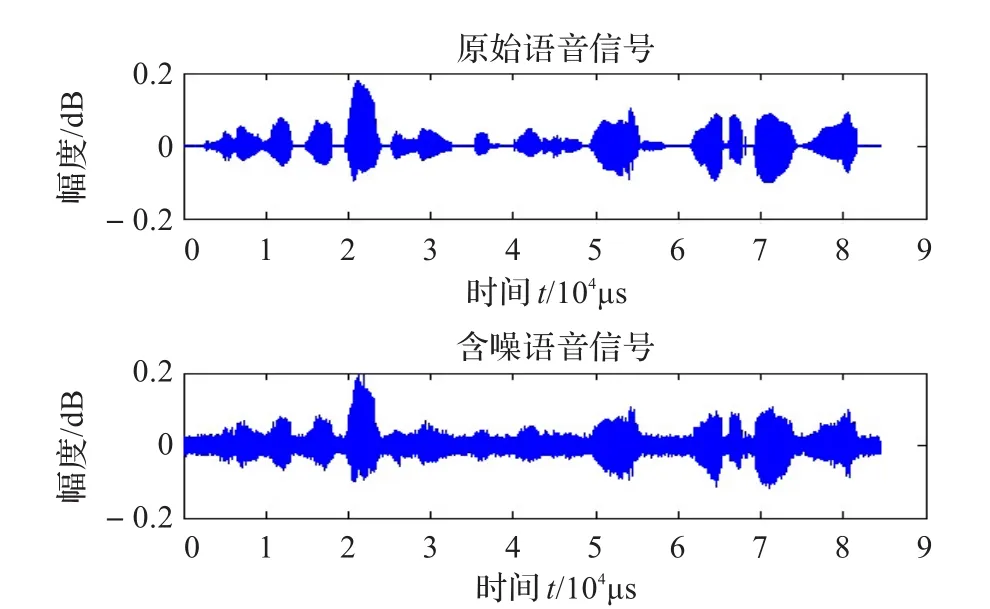
图3 原始语音信号与含噪语音信号

图4 新阈值函数的去噪结果

从图中可以看出，用新阈值函数进行小波阈值去噪后，保留了较多的原始语音信号，减小了噪声信号的影响。试听对比后发现，用新阈值函数进行去噪后的语音片段虽还有少量噪音，但能够清晰听懂语音片段的有用信息。

4.3 新阈值函数与硬阈值函数和软阈值函数的比较

选择α=0.1，n=100，利用“coif5”小波进行4层小波分解，在不同输入信噪比下，比较了本文提出的阈值函数和硬阈值函数，软阈值函数，折衷阈值函数的去噪效果。如表3所示。

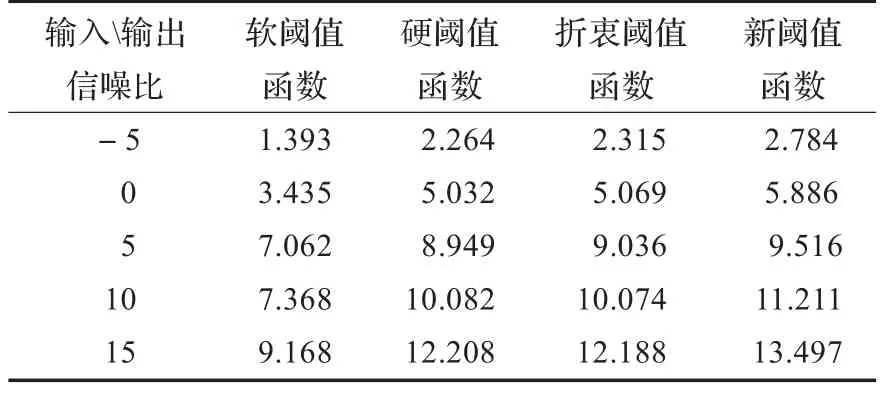
表3 四种不同阈值函数的比较 dB

通过比较可以看出，在不同信噪比下，新阈值函数的去噪效果都明显优于硬阈值函数，软阈值函数和折衷阈值函数。

四种阈值函数去噪后的语音信号如图5所示。

从图中可以看出，软阈值函数处理后，语音信号有明显的失真；硬阈值处理后语音信号比较尖锐，毛刺较多；折衷函数处理后，削去了较多的信号；新阈值函数处理后，语音信号比较平滑，和原始信号最为接近。

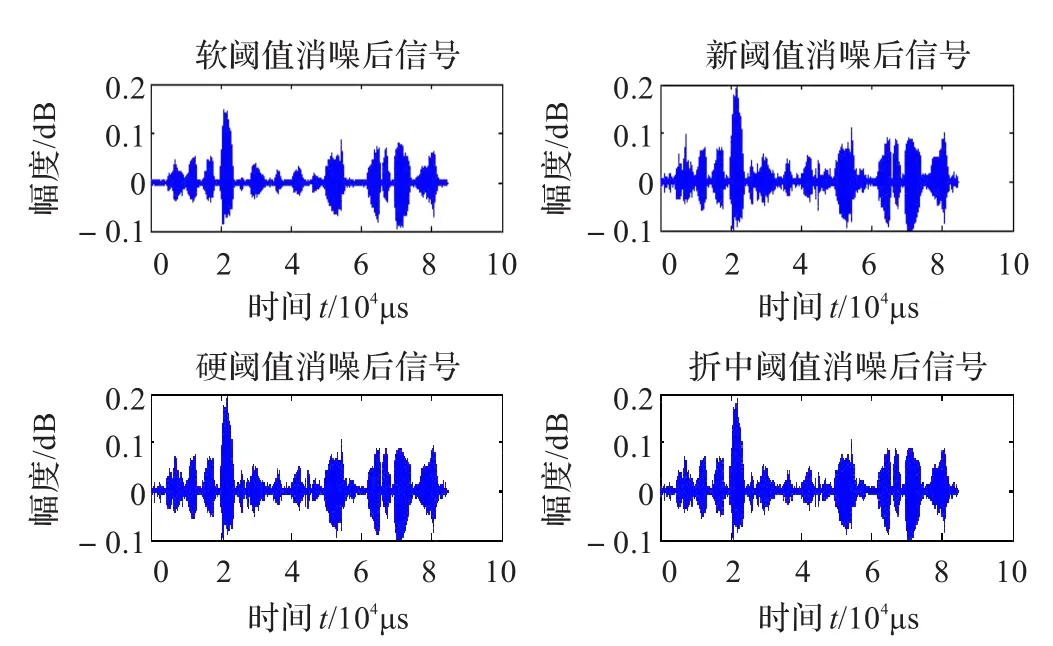
图5 四种阈值函数去噪效果

5 结束语

在小波阈值去噪中，小波基函数的选取，阈值的确定和阈值函数的处理至关重要。Donoho提出的固定阈值和传统的硬阈值、软阈值函数都存在一些缺陷，使语音信号的去噪效果不够理想。本文提出了一种新的阈值函数，并使用了改进的阈值，通过三组实验分别选取了适于本语音信号的最优小波基，新阈值函数的最优参数，并和硬阈值法、软阈值法进行了比较。通过实验可以看出，本文提出的阈值函数具有更好的去噪性能，能更多地保留原始语音信号，去除背景噪声。无论是主观感受还是信噪比的提高程度都明显优于传统方法和改进算法。

[1]袁莉芬，何怡刚.一种改进型的小波变换语音去噪算法[J].现代电子技术，2009（18）：120-122.

[2]Mallat S，Hwang W L.Singularity detection and processing with wavelets[J].IEEE Τrans on Inform Τheory，1992，38（2）：617-643.

[3]Xu Y S，Weaver J B，Healy D M.Wavelet transform domain filters：a spatially selective noise filtration technique[J].IEEE Τransactions on Image Processing，1994，3（6）：747-757.

[4]Donoho D L.De-noising by soft-thresholding[J].IEEE Τrans on Information Τheory，1995，41（3）：613-627.

[5]王拴中,朱玉田.改进小波阈值去噪法的对比性仿真实验与分析[J].噪声与振动控制，2012（1）：128-132.

[6]Donoho D L，Lain M J.Ideal spatial adaptation by wavelet shrinkage[J].Blomelrika，1994，81（3）：425-455.

[7]周夕良.基于μ律拟合的小波自适应阈值去噪算法[J].计算机工程与应用，2011，47（27）：141-143.

[8]冯象初，甘小冰，宋国乡.数值泛函与小波理论[M].西安：西安电子科技大学出版社，2003：159-164.

[9]陶红艳，秦华峰，余成波.基于改进阈值函数的小波域去噪算法的研究[J].压电与声光，2008，30（1）：93-95.

[10]马宏锋，高晶晶，党建武，等.基于最优小波基函数的语音增强研究[J].通信技术，2010，43（12）：135-137.

[11]郭兴明，柯明，肖守中.3σ规则和μ律阈值法在心音信号去噪中的应用[J].计算机工程，2010，36（7）：279-281.

[12]张君昌，刘红，姜菲.基于清浊音分离的优化小波阈值去噪方法[J].计算机工程与应用，2009，45（31）：130-133.

WANG Rui,ZHANG Youchun

School of Mechanical and Electronic Information,China University of Geosciences（Wuhan）,Wuhan 430074,China

Τo overcome the disadvantage in traditional wavelet threshold de-noising approach,the hard threshold function is discontinuous while the soft threshold function has fixed deviation;a new threshold function is proposed.An adaptive threshold is proposed to enhance the fixed threshold put forward by Donoho.Under the Matlab environment,three experiments are separately carried to select the optimum wavelet base,the optimum parameters of the new threshold function and to compare the new threshold function with traditional threshold functions such as the hard threshold function,the soft threshold function and the compromise threshold function.Experimental result shows that the new threshold function is more effective to enhance the Signal-to-Noise Ratio and to improve the quality of the de-noised speech signal.

wavelet transform;threshold de-noising;threshold function;adaptive threshold;optimum wavelet base

针对传统小波阈值去噪法中硬阈值函数不连续，软阈值函数有固定偏差的缺点，提出一种新的阈值函数。对Donoho的固定阈值进行改进，提出一种自适应的阈值。在Matlab环境中，分别进行了实验选取最优小波基，新阈值函数的最优参数以及新阈值函数与传统硬阈值函数，软阈值函数和折衷阈值函数的对比。实验结果表明，新的阈值函数能更有效地提高语音信号的信噪比，改进语音质量。

小波变换；阈值去噪；阈值函数；自适应阈值；最优小波基

A

ΤP306.1

10.3778/j.issn.1002-8331.1211-0364

WANG Rui,ZHANG Youchun.New threshold function in wavelet threshold de-noising.Computer Engineering and Applications,2013,49（15）：215-218.

王瑞（1988—），女，硕士研究生，研究领域为信号处理；张友纯（1954—），男，教授，研究领域为通信与信息系统、计算机应用技术。E-mail：keria1988@yahoo.cn

2012-11-29

2013-01-22

1002-8331（2013）15-0215-04