基于格林函数的图像增强算法

席志红，赵蓝飞，邢代玉

哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001

基于格林函数的图像增强算法

席志红，赵蓝飞，邢代玉

哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001

1 引言

随着对于图像处理技术的深入研究，数字图像越来越广泛地应用于各个领域。绝大多数的图像都存在图像质量不高，主观效果不佳等缺陷，这些缺陷极大地约束了后续的图像处理算法的效果。为了解决该问题，应用最为广泛的是图像增强技术。较优秀的图像增强算法能够突出图像的局部或整体特性，改善图像的质量，增强图像的视觉效果。

图像增强算法有很多，这些算法都能够在一定程度上改善图像的主观视觉效果，但这些算法同样存在一定的缺陷，例如直方图均衡化方法[1]能够有效地提高图像的整体对比度，但是图像局部区域内的对比度下降，该方法易造成灰度级的过度合并导致增强图像丢失部分原始图像的细节，增强图像的质量有所下降。Retinex是一种关于人类视觉的光亮度和色彩感知的模型，该模型被广泛地应用于图像增强领域[2]。虽然Retinex模型采用分层式的结构，能够有效地提高图像的对比度，但是增强图像存在严重的光晕现象[3]，导致高对比度的图像边缘的细节被覆盖。非线性灰度拉伸法[4]对于对比度的提高有较明显的效果，但是该方法未考虑人眼的主观视觉效果，并且灰度级的合并造成图像信息熵的减小，增强图像的视觉效果较差。

针对以上算法的缺陷，本文提出了一种基于格林函数的图像增强算法。由于Retinex模型分离出的细节层包括了图像的细节信息，光照层包括了图像的对比度信息[5]，所以为了尽可能地保持图像的细节，在保持细节层不变的前提下，单独对光照层进行图像增强。由于格林公式是基于平面区域，还需要已知区域的狄利克雷边界条件[6]，电像法求解格林函数的前提条件是具有规则、对称的区域[7]，所以首先采用“二次分块”将原始图像分割为多个圆形区域，通过灰度映射得到各圆形区域的边界像素的灰度值。由于梯度域包含了原始图像的部分信息，为了保证增强图像与原始图像具有较高的相似度，在保持梯度域信息一致的前提下，将求解光照区域内像素的亮度值转化为求解相应的泊松方程。采用电像法得到各光照区域的格林函数，根据以求得的狄利克雷边界条件以及平面区域的第二格林公式得到泊松方程的解，即光照区域内各像素的增强亮度值。由于曲线积分的复杂度较高，不利于实时处理，提出一种边界采样方法，有效地降低了格林函数的复杂度。最后将增强后的亮度层与细节层相乘得到增强图像。实验证明，该算法能够在提高对比度的同时，有效地保持原始图像的细节信息，增强图像的主观视觉效果较高。

2 Retinex模型与泊松方程

2.1 Retinex模型

根据Retinex理论，图像由反射层与光照层构成，Retinex模型可表示为：

式中R、I、S分别代表细节层、光照层和原始图像。其中细节层包含了原始图像的细节信息，光照层决定了图像的对比度以及动态范围。Retinex理论核心的部分是得到光照层I，很多学者在Retinex模型的基础上提出了一些光照估计算法。其中应用范围最广的是单尺度SSR（Single Scale Retinex）算法[8]。SSR算法通过高斯函数与图像进行卷积估计光照图像，表达式如下：

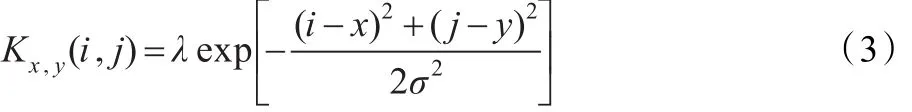
式中σ是环绕函数的尺度，λ是归一化常数。SSR算法虽然能够估计光照变化较缓慢区域内的亮度信息，但是光照变化较剧烈的图像边缘，SSR算法易造成光晕[9]。

2.2 基于梯度域的泊松方程

算法原理如下：令梯度图像是F，根据梯度算子的性质，光照层I和F满足如下关系：

式中∇是梯度算子。假设增强后的光照层表示为，根据梯度的一致性则可以表示为：

对于1维数据，直接对式（5）的两边进行积分就能够得到对于2维数据，由于方程（5）无解[10]，所以无法直接积分得到增强后的光照图像。Fattal等人[10]采用式（6）的形式：

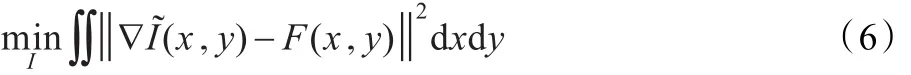
间接得到式（5）的解。令P，根据变分法原理，式（6）满足欧拉-拉格朗日方程。

将P带入式（7）得到如式（8）的泊松方程：

式中D是拉普拉斯算子，div是散度算子，满足如下关系：

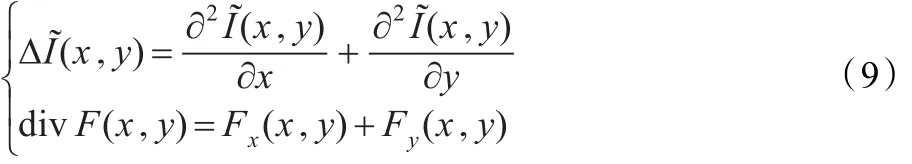
3 本文算法

3.1 算法原理

光晕的存在是由于算法单纯地考虑像素间的空间关系，忽略了像素间的灰度关系所造成的光照图像的边缘附近产生较严重的灰度突变。由于双边滤波在考察像素位置关系的基础上综合了像素的灰度变化信息，所以双边滤波能够有效地抑制光晕。双边滤波与SSR算法唯一的不同之处在于对卷积核的选取，双边滤波的卷积核如下：

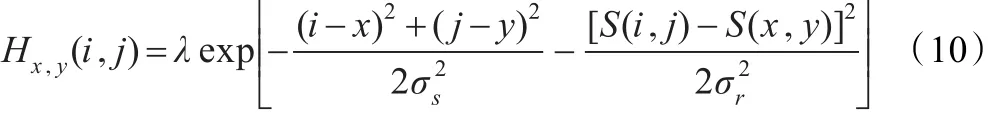
式中分别是空域以及灰度域的尺度。

由于双边滤波器的形状是由像素的灰度以及位置信息综合决定的，所以时间复杂度是O(r2)远大于SSR的O(r)，其中r是卷积窗尺寸。本文采用文献[11]提出的快速双边滤波算法估计光照图像。该算法通过快速中值滤波以及多列同步的并行算法减小了双边滤波算法的冗余信息，将算法的复杂度降低为O(lbr)。

为了保证增强图像与原始图像在梯度域上保持一致，将求解增强后的光照图像转化为求解如式（8）的泊松方程。根据2.2节所述，在原始图像光照层的梯度图像已知的情况下，只要求得如式（4）的泊松方程的解，得到增强后的光照图像I，再将I替换为式（1）的原始光照图像I就能得到保持细节的增强图像。

3.2 格林公式求解泊松方程

解泊松方程的方法有很多，例如格林公式法、快速傅里叶变换法、中心差分法、多重网格法[12]等。本文采用基于狄利克雷边界条件的平面第二类格林公式法求解式（8）的泊松方程，其中狄利克雷边界条件能够控制平面区域整体的亮度情况，也就是说只要将亮度较低或曝光度较高的区域的边界像素的亮度值映射到适于人眼分辨的亮度值，再根据格林公式就能够得到增强的光照图像。

假设ω是平面闭区域，∂ω是区域边界，边界条件ω*已知，r是ω内任意一点，则式（9）满足狄利克雷边界条件，表达式如下：

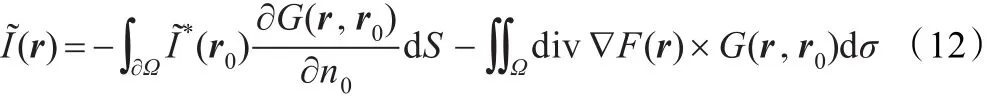
根据平面第二格林公式，式（11）的解可以表示为：式中n0是∂ω的外法线方向，r0是平面区域ω内点源电荷的位置，G(r，r0)是格林函数满足点源函数性以及边界的齐次性，表达式如下：

式中和div∇F(r)已知，只有格林函数G未知，因此只要构造出满足点源函数性以及边界齐次性的格林函数就能够得到式（12）的解。

3.3 电像法构造格林函数

常用的格林函数的构造方法是电像法，该方法能够得到规则、对称区域的格林函数。假设一个平面圆形区域ω，该区域内部的介电常数ε=1，ω内任一点放置一个电量为q的标准正点电荷，边界∂ω由m个不重复的点组成且满足关系∂ω∈{b1，b2，…，bm}，∀bi∈R2。据电像法原理，点电荷在任意边界点处形成的感应电荷的等效电荷q′在圆心与q点的延长线上，且位于圆外。图1为点电荷、边界点以及等效电荷示意图。

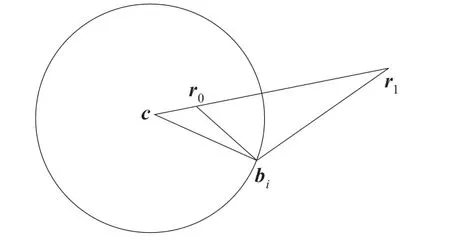
图1 电荷、边界点以及等效电荷示意图

图1中c是圆心，r0是点电荷，r1是等效电荷，bi点是任意的边界点并且满足关系：

又因为∠r0cbi=∠bicr1，推出Dr0cbi相似于Dbicr1，得到以下关系：

式中R是圆的半径。根据电磁场理论，格林函数G(r，r0)描述了点电荷r0在r的电势，对于无界空间中任意一点的格林函数可以表示为：

对于图1的圆形区域，区域内一点r的电势由r0在无界空间中产生的电势与边界等效电荷产生的电势叠加而成，此时G(r，r0)可以表示为：

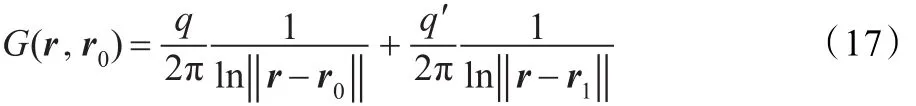
由于格林函数具有边界齐次性，即任意边界点bi处的电势为0，所以任意边界bi的格林函数恒等于0，表达式如下：

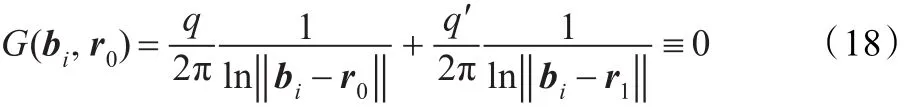
整理式（14）、（15）并将结果带入式（18）得到：

将式（19）带入式（17）得到圆形区域格林函数的表达式：

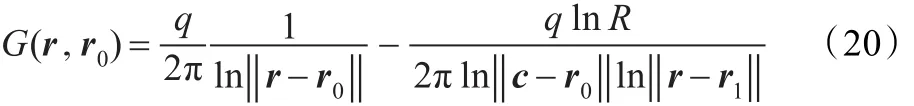
将式（20）带入式（12），得到泊松方程的解，即增强后的光照图像。

3.4 边界采样

根据式（12），求解区域内部像素的灰度值等价于对整个区域的边界求格林函数的第二类曲线积分，该算法的复杂度是O(mn)，其中m是边界点的个数，n是区域内的像素总数。此时算法的复杂度较高，不利于实时性处理。这里通过边界等间隔采样的方法，降低算法的复杂度。

算法原理如下：首先对于边界∂Ω进行间距为d的等间距采样，得到的边界点集可以表示为其中区域内任意一点xi到采样后边界点bc欧氏距离是由式（12）可知，当点电荷与边界点距离较小时，该边界点对于曲线积分的“贡献”较大，反之亦然。根据这个结论，设置一个衡量距离的阈值λ，当阈值满足以下条件时：

说明采样后的边界点与xi的距离较大，对于曲线积分的贡献较小，此时附近的采样前的边界点对于曲线积分的影响可以直接用代替；否则边界点与xi的距离较小，需要进一步增加附近的边界点的采样密度。图2是区域内一个任意位置的点电荷以及对应的边界采样得到的点集。

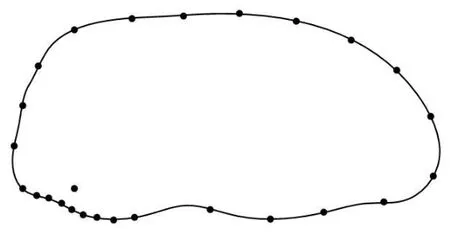
图2 边界采样原理

从图2可以看出，距离该点越近，边界采样得到的有效的边界点越多，反之亦然。所以当满足式（21）时，有效的边界像素减少，所以复杂度较低。

3.5 自适应亮度映射

根据式（12），只要得到格林公式作用的平面区域的狄利克雷边界条件，就能够得到区域的内像素的灰度值，所以边界像素的灰度值控制该平面区域内像素的整体亮度情况。虽然显示器能够显示较为广阔的亮度范围，但是人眼对于不同亮度值的敏感程度是不相同的。例如随着亮度的降低，人眼分辨细节以及局部对比度的能力下降，造成图像质量下降，强光对人眼的刺激性较强，导致图像细节被高光所淹没。

综上所述，对于较暗的平面区域，需要适当提高边界像素的亮度值，对于较亮的区域，需要适当降低边界像素的亮度值，将边界条件带入到格林公式中，得到泊松方程的解，即从整体上保证人眼的视觉效果。本文采用文献[13]提出的分段式自适应亮度值，将边界像素的亮度值映射到适于人眼观察的亮度值。该算法采用如表1所示的分段映射。

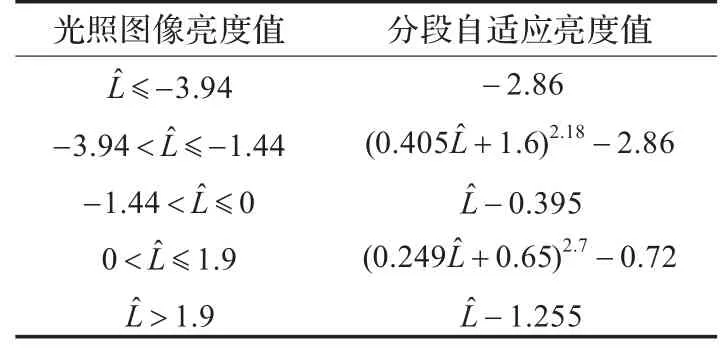
表1 分段自适应亮度映射 (cd·m-2)

表中Lˆ是亮度值，单位是坎德拉(cd/m2)。由于灰度图像采用灰度值衡量像素的亮度信息，所以无法直接采用表1的分段自适应亮度映射方法。首先需要将灰度值转化为相应的亮度值，转换方法如下：假设Lmin、Lmax分别是显示器的最小与最大亮度值，像素的灰度范围是0～255，则像素的灰度转换到亮度的公式如下：

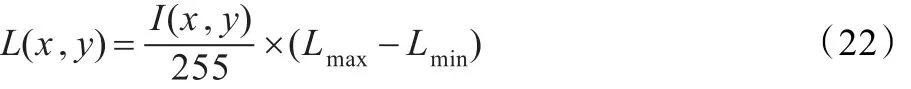
式中I是通过快速双边滤波得到的光照图像，L是对应的亮度图像。得到亮度图像L后，将L带入表1得到各像素自适应的亮度值。最后还需通过式（21）将亮度值转化为灰度值，得到对应的灰度图像。

3.6 算法步骤

根据前文所述，电像法首先需要将图像分割为一组对称的平面闭区域，再根据区域的狄利克雷边界条件，求得泊松方程的解。由于电像法只适用于规则、对称的区域，这里采用“二次分块”的方法将图像划为多个规则的圆形子块，通过电像法获得每个子块对应的泊松方程的解，最后合并各个子块的解得到增强图像。算法具体步骤如下：

步骤1通过快速双边滤波将光照层与细节层分开。

步骤2按照原始图像尺寸将光照图像划分为多个相切的圆形区域，如图3所示。

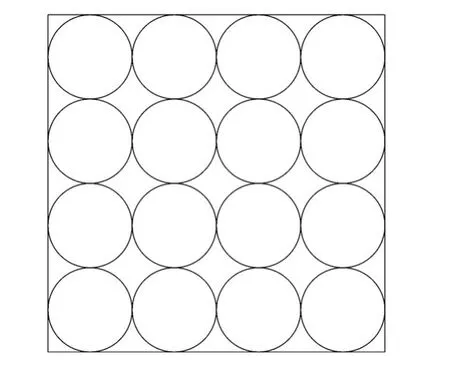
图3 初次分块

步骤3对全部边界点进行亮度分段映射，得到所有区域的第一类边界条件。

步骤4抽出一个区域，在区域内任取一个点放置电量为q的点电荷，对该区域进行间隔为d的边界采样算法，根据式（20）解得该区域的格林函数。

步骤5将格林函数带入式（12）求出区域内各像素的灰度值，并将已经解出的像素做标记。

步骤6重复步骤4～5，直到遍历完全部分割出的圆形区域。

步骤7采用二次分块将剩余的像素划入各个子块，如图4所示，对于超出图像边界的子块，采用复制边界的方法对原始图像进行扩展。

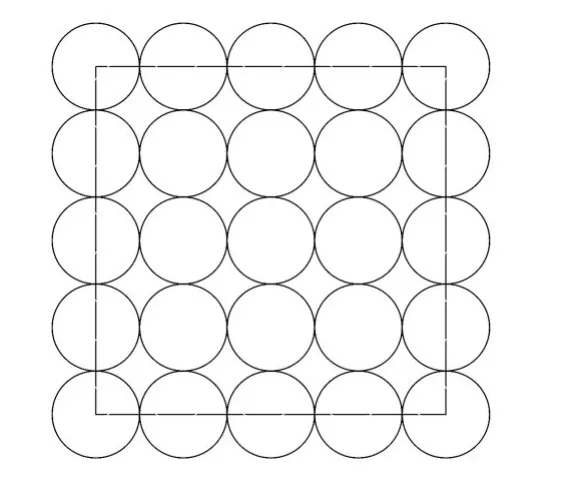
图4 二次分块

步骤8对于二次分块出来的区域，在该区域内的未标记像素中任选一点用来放置点电荷，对该区域进行间隔为d的边界采样算法，根据式（20）解得区域的格林函数。

步骤9将格林函数带入式（12）解得未标记像素的灰度值。

步骤10重复步骤8～9直到遍历完全部二次分块的区域。

步骤11将增强后的光照图像带入Retinex模型得到增强图像。

由于第一次分块解得的像素灰度值已经完全涵盖了二次分块得到的区域边界条件，所以二次分块后，并没用采用如步骤3的亮度分段映射得到狄利克雷边界条件。

4 实验结果与分析

4.1 主观视觉效果

图5 原始图像

本文采用的硬件平台是Pentium Dual-Core 2.70 GHz处理器，2.00 GB内存，软件仿真环境是Microsoft Visual Studio 2010。采用色深24 bit/pixel的位图文件作为输入和输出。图5是原始图像，图6、7是各算法得到的增强图像，其中本文算法采用的参数是：采样间隔d=4，圆形区域半径R=8，距离阈值λ=2，SSR算法的空域尺度σ2=80，非线性灰度拉伸的校正系数是2.0。

图6 cameraman的增强图像

图7 Lena的增强图像

从图6、7可以看出，几种增强算法都在一定程度上提高了图像的整体对比度，增强图像的主观效果有一定的差异。其中直方图均衡化方法图像造成灰度级的过度合并导致增强图像丢失部分原始图像的细节，造成图像的质量下降。SSR算法存在严重的光晕现象，导致高对比度的图像边缘的细节被覆盖。非线性灰度拉伸法未考虑人眼的主观视觉效果，并且灰度级的合并造成图像信息熵的减小，增强图像的视觉效果较差。本文算法得到的增强图像不但提高了图像的整体对比度，增强图像的细节较丰富，人眼视觉效果较高。图8是不同的采样间隔对应的增强图像。

由图8可以看出不同的采样间隔得到的增强图像的效果有差异。采样间隔太大导致采样后的边界点无法重建区域内像素的灰度值，并且根据内奎斯特采样定律，采样频率过小易造成频谱的重叠。

4.2 评价指标

由于文献[14]提出并证明了在无参考图像条件下衡量图像清晰度的方法（CSFNRS）满足评价指标的准确性、单调性、一致性，所以本文采用该评价方法衡量各算法对应的增强图像的质量。当CSFNRS越大时，表明增强图像越清晰，图像质量越高。各算法对应的评价系数如表2、3所示。

图8 cameraman的增强图像

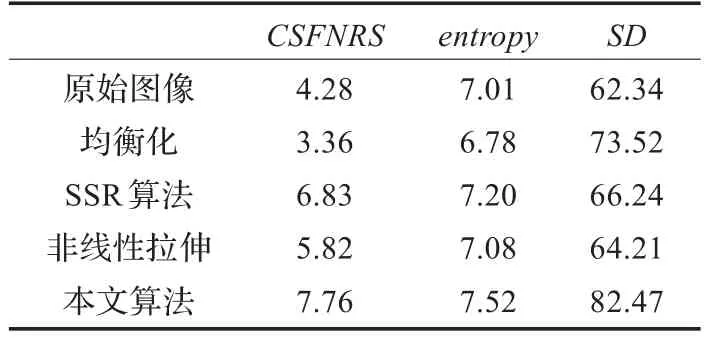
表2 cameraman的评价指标

表3 Lena的图像评价指标

表中信息熵（entropy）描述了图像包含的信息量的大小[15]，方差（Standard Deviation，SD）描述了图像的整体对比度[16]。从表2、3可以看出，相比于其他算法，本文算法得到增强图像所包含的信息量，清晰度以及对比度都比较高，与图6和图7的增强图像的主观效果保持一致。

采用文献[17]提出的基于梯度的结构相似度的评价指标（GSSIM）。GSSIM利用人眼对于梯度信息较为敏感的特性，计算出参考图像与增强图像的梯度域信息的差异。如果GSSIM越小，说明增强图像在结构和细节方面与原始图像保持一致。增强图像与原始图像的形似度评价指标如表4所示。

表4中，PSNR是图像的峰值信噪比[18]，单位是dB。PSNR反映了增强图像与原始图像的相似度，PSNR越小时，说明增强图像在灰度信息方面与原始图像较为相似。从表4可以看出，本文算法对应的GSSIM和PSNR是最小的，说明本文算法能够有效地保持原始图像的结构、梯度信息等信息。

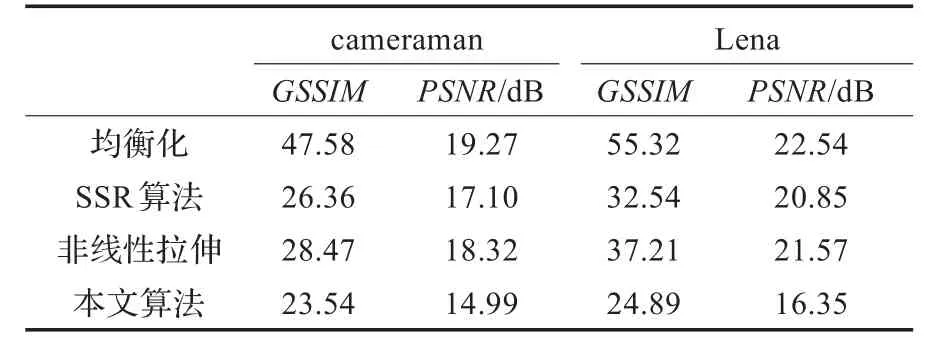
表4 图像的相似度指标

图9是在不同参数条件下的峰值信噪比。

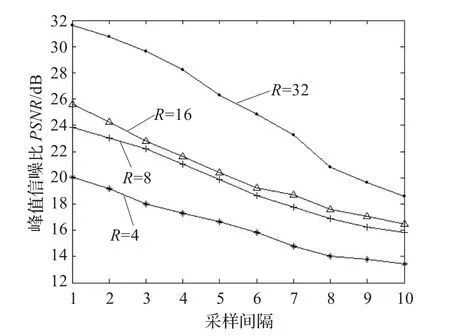
图9 不同参数对应的峰值信噪比

从图9可以看出在区域半径R相同的条件下，随着采样间隔的增加，PSNR的值越来越小，其原因是随着间隔的变大，曲线积分可供参考的边界点越来越少，导致积分结果无法精确地得到泊松方程的解。但是随着采样间隔的增加，算法的复杂度越来越大，表5是不同参数对应的算法复杂度。

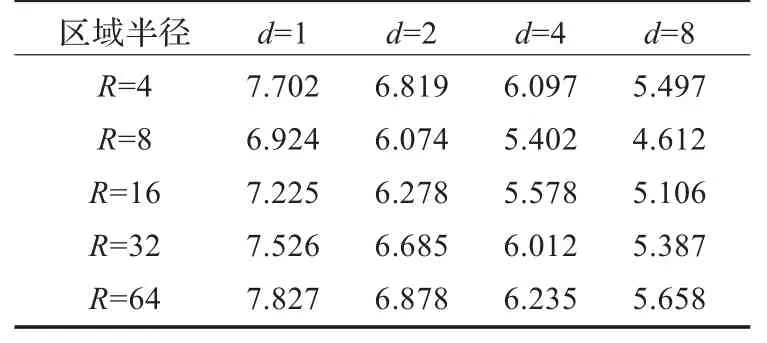
表5 不同参数下的算法复杂度 dB

表5中，算法复杂度的单位是dB。经过大量实验，得到R=8，d=4时，增强图像的视觉效果较好，并且算法的复杂度较低。

5 结束语

为了解决传统的图像增强算法的缺陷，本文提出了一种图像增强算法。算法将求解增强图像转化为求解梯度域内的泊松方程，通过电像法求解格林函数，通过边界采样方法降低算法复杂度，通过灰度映射得到狄利克雷边界条件，通过格林函数求解泊松方程，得到最终的增强图像。实验证明该算法能够有效地提高对比度，增强图像具有较丰富的细节和较高的清晰度。

[1]陈文飞，廖斌，许雪峰，等.基于Piecewise直方图均衡化的图像增强方法[J].通信学报，2011，32（9）：153-160.

[2]Majumdar J，Nandi M，Nagabhushan P.Retinex algorithm with reduced halo artifacts[J].Defence Science Journal，2011，61（6）：559-566.

[3]Morel J M，Petre A B，Sbert C.A PDE formalization retinex theory[J].IEEE Τransactions on Image Processing，2010，19（11）：2825-2837.

[4]刘艳莉，陈燕，桂志国.基于灰阶熵的模糊对比度自适应图像增强算法[J].测试技术学报，2012，26（5）：441-445.

[5]纪则轩，陈强，孙权森，等.基于双边滤波的单尺度Retinex图像增强算法[J].微电子学与计算机，2009，26（10）：99-102.

[6]Polyanin A D，Zaitsev V F.Handbook of exact solutions for ordinary differential equations[M].2nd ed.Boca Raton：Chapman&HallCRC Press，2003：72-80.

[7]王雪君.电动力学解题指导[M].北京：北京师范大学出版社，1998：32-33.

[8]许欣，陈强，王平安，等.消除光晕现象的快速Retinex图像增强[J].计算机辅助设计与图形学学报，2008，20（10）：1325-1331.

[9]Michael K N，Wei W.A total variation model for retinex[J]. SIAM Journal on Imaging Sciences，2011，4（1）：345-365.

[10]Fattal R，Lisehinski D，Werman M.Gradient domain high dynamic range compression[J].ACM Τransactions on Graph，2002，21（3）：249-256.

[11]沈丰，赵宇明.基于实时Retinex与双边滤波的图像增强算法[J].计算机应用与软件，2009，26（11）：234-238.

[12]刘冬梅.高动态范围图像显示算法的研究[D].上海：上海交通大学出版社，2009.

[13]Larson G W，Rushmeier H，Piatko C.A visibility matching tone reproduction operator for high dynamic range scene[J]. IEEE Τransactions on Visualization and Computer Graphics，1997，3（4）：291-306.

[14]范媛媛，沈湘衡，桑英军.基于对比度敏感度的无参考图像清晰度评价[J].光学精密工程，2011，19（10）.

[15]周书敬，高延安.基于信息熵改进的粒子群算法在桁架结构优化设计中的应用[J].工程设计学报，2012，19（5）：340-344.

[16]张涛，平西建，徐长勇.基于图像平滑度的空余LSB嵌入的检测算法[J].计算机辅助设计与图形学学报，2006，18（10）：1607-1612.

[17]杨春玲，陈冠豪，谢胜利.基于梯度信息的图像质量评判方法的研究[J].电子学报，2007，35（7）：1313-1317.

[18]王益艳.基于平滑核的广义变分法去噪模型[J].重庆师范大学学报：自然科学版，2010，27（6）：59-63.

XI Zhihong,ZHAO Lanfei,XING Daiyu

College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China

As the traditional image enhancement is suffered from uncomfortable details and visual effect,this paper proposes a new algorithm.Τhe details are ensured by using Retinex model.Τhe consistency in gradient domain between original image and restoration is guaranteed by solving the Poission equation.It adopts the adaptive luminance method to obtain the Dirichlet boundary condition.Τo reduce the complexity,boundary sampling method is executed.By making comparison with restorations, it shows that this algorithm effectively improves contrast,meanwhile the restorations represent excellent effect of sense.

image enhancement;Retinex;Poission equation;Green’s function;gradient domain;method of images;Dirichlet boundary condition

由于传统的图像增强算法得到的增强图像存在细节的缺失，主观效果较差等缺陷，提出了一种图像增强算法。通过Retinex模型保证了增强图像具有较突出的细节特性；通过求解泊松方程满足了增强图像与原始图像在梯度域的一致性；采用自适应亮度映射得到适于显示的边界条件；对区域的边界进行采样降低算法的复杂度。实验对比了几种图像增强算法得到的增强图像以及相关的评价系数，验证了该算法能够有效地提高图像的对比度，增强图像的主观视觉效果较高。关键词：图像增强；Retinex；泊松方程；格林函数；梯度域；电像法；狄利克雷边界条件

A

ΤP391.41

10.3778/j.issn.1002-8331.1303-0146

XI Zhihong,ZHAO Lanfei,XING Daiyu.Image enhancement algorithm based on Green function.Computer Engineering and Applications,2013,49（15）：204-209.

国家自然科学基金（No.60875025）。

席志红（1965—），女，博士，教授，博导，研究领域为数字图像处理，嵌入式系统设计，模式识别等；赵蓝飞（1985—），男，博士研究生，研究领域为数字图像设计，嵌入式系统设计；邢代玉（1988—），女，硕士研究生，研究领域为计算机图形学，信息处理等。E-mail：zlf82563144@163.com

2013-03-12

2013-05-09

1002-8331（2013）15-0204-06

◎信号处理◎