自适应的最大散度差图像阈值分割法

祝 贵，杨恢先，岳许要，冷爱莲，何雅丽

1.湘潭大学 光电工程系，湖南 湘潭 411105

2.湘潭大学 能源工程学院，湖南 湘潭 411105

自适应的最大散度差图像阈值分割法

祝 贵1，杨恢先1，岳许要1，冷爱莲2，何雅丽1

1.湘潭大学 光电工程系，湖南 湘潭 411105

2.湘潭大学 能源工程学院，湖南 湘潭 411105

1 引言

图像分割是指将一幅图像分成若干个互不交叠的、有意义的、具有相同性质的区域，它是图像分析、理解和模式识别中基础而关键的问题，也是图像处理中一个难点。阈值法是一种简单而广泛使用的方法，许多研究人员和学者对阈值的自动选取进行了大量的研究，并提出了最大熵法、最大相关性法及最大类间方差法（即Otsu法）[1-3]等方法。其中基于直方图的最大类间方差法因简单实时性好而被广泛应用，但在图像背景和目标面积相差较大，或图像的信噪比较低时，最大类间方差法的分割效果不理想甚至不能有效地分割。文献[2]提出了一种二维Otsu图像分割算法，该方法同时包含了像素的灰度信息和邻域空间信息，比一维Otsu算法具有更强的抗噪能力。然而，其算法涉及多次平方运算，计算复杂程度较高，且阈值选择标准仅考虑到类间方差的最大性，未考虑到目标和背景二类像素的自身内聚性，因而常导致分割后目标轮廓的细节比较模糊。也有学者仅从类内散度出发提出新的阈值分割方法[4-5]，但又因没有兼顾类间散度，分割效果依然不理想。

针对Otsu阈值分割法的不足，文献[6]通过引入模式识别中Fisher准则而提出一种将Fisher评价函数图像分割的准则函数（该方法简记为Fisher准则法），该评价函数使得类间方差最大且类内方差最小时取得最佳分割阈值，类内方差可能是奇异的而且类内方差在分离性中的作用是固定的，导致该算法不稳定。文献[7]对Fisher准则作了必要的修正，并基于新的鉴别准则设计了最大散度差分类器，文献[8]将最大散度差分类的思想运用到图像分割中，通过调节C的取值控制类内方差在分离性中的作用，达到了比较好的分割效果，证明了最大散度差分类思想的有效性，但是C的取值不能自适应地确定，从而使该方法难以运用在实时处理中。在此基础上，提出一种自适应地得到参数C的方法，得到自适应的最大散度差（Adaptive Maximum Scatter Difference，AMSD）的图像阈值自动分割方法（记为AMSD分割法），通过对大量图片的有效分割证明了该方法具有很好的稳定性，且分割效果较好。

2 最大类间方差（Otsu）分割方法

对于一幅大小为M×N的灰度图像，灰度级范围为{0，1，…，L-1}，记灰度级为i的像素的频数为fi，则该像素出现的概率为：

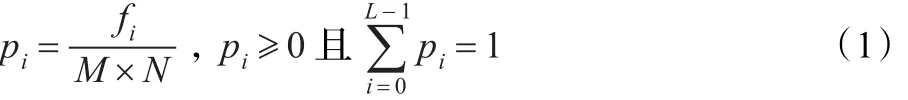
Otsu阈值分割法就是以最大类间方差为评价函数得到一个阈值k，以该阈值将图像各像素按灰度分成(I0，I1)两类，像素灰度级范围为{0，1，…，k}划为I0类中，像素灰度级范围为{k+1，k+2，…，L-1}划为I1类中。那么I0类和I1类两类图像的概率p0(k)、p1(k)和均值u0(k)、u1(k)分别为：

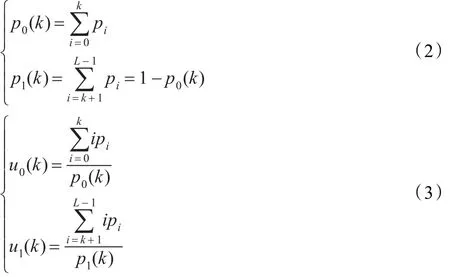
图像的总体均值为：

I0和I1类的类间方差为：

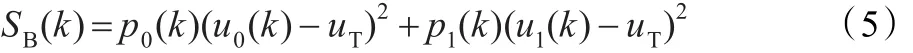
Otsu分割法以式（5）为评价函数，表征了I0和I1两类图像到图像中心的距离和，若在灰度阈值为k时I0和I1类的类间方差最大，此时I0和I1类到图像中心距离和最大，I0和I1类分得最开，取该灰度值为最佳阈值并记为k*，即

遍历各个灰度级并求对应的SB(k)，找到最佳阈值k*。在图像各像素中，灰度小于阈值k*的灰度置为0，灰度大于k*的灰度置1，从而将图像的背景和目标分离开来，得到分割后的二值化图像。

3 最大散度差阈值分割法

3.1 最大散度差分割法原理

当I0和I1类的类间方差最大时，表示I0和I1两类的距离最大，分离得越开；当类内方差最小时，各类内像素点到类中心的距离越小，表示各类的内聚性越好；同时考虑类间方差和类内方差，定义类间方差减去C倍类内方差为散度差作为分离性度量。类间方差达到最大且类内方差达到最小时散度差最大，用使散度差达到最大时的灰度值作为图像分割的最佳分割阈值。

I0和I1两类图像的类内方差分别为：

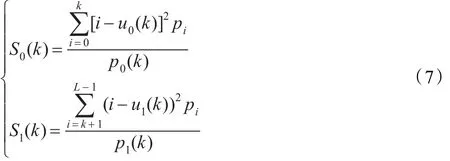
图像的类内方差为：

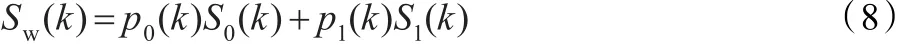
由于Otsu分割法中类间方差会使总体均值偏向峰值大的一侧，进而导致得到的阈值向峰值大的一侧“漂移”，为此定义新的类间方差：

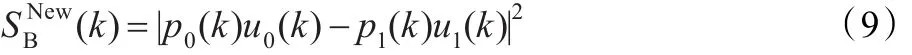
则Fisher准则和最大散度差准则的数学定义分别为：

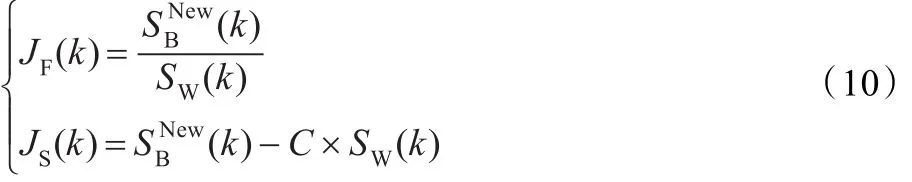
使式（10）取得最大值的灰度值k*为最大散度差分割法分割图像的最佳阈值，即

3.2 参数C的初步确定

事实上，最大散度差准则中参数C的取值对分类的结果影响很大，因此要使图像分割取得好的效果必须对参数C选择合适的值。图像分割实质上可以看成像素灰度数据的聚类[9-10]和分类问题，各像素点即为分类的样本点，将像素点的灰度值i视为样本值。I0和I1类的样本均值u0(k)、u1(k)为I0和I1类的中心，将模糊概念引入类间方差、类内方差得如式（12）的模糊类间方差SFB(k)、如式（13）的模糊类内方差SFW(k)，进而得出模糊最大散度差准则表达式式（14）。

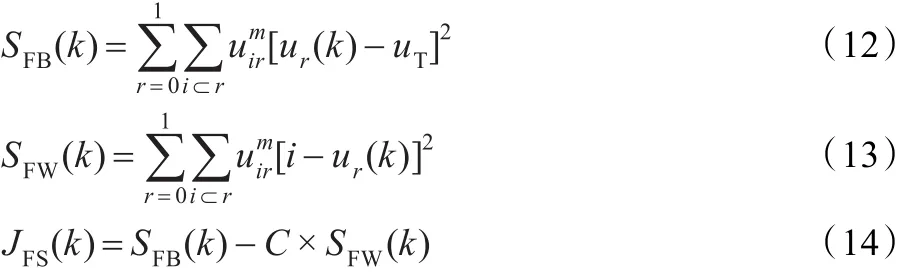
式（12）、式（13）中uir为灰度值为i的像素点隶属于类Ir(r= 0，1)的隶属度，m为模糊指数，且有：

根据拉格朗日数乘法求模糊最大散度差，拉格朗日公式：

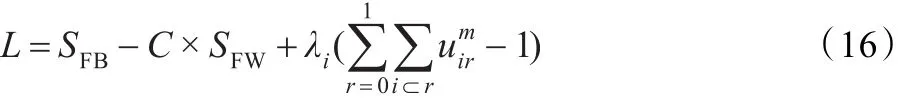
对uir求偏导数，并令：

解得：

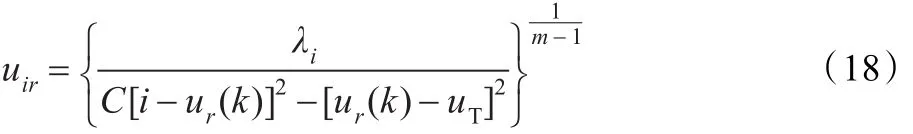
将式（18）的结论代到式（15）中得：

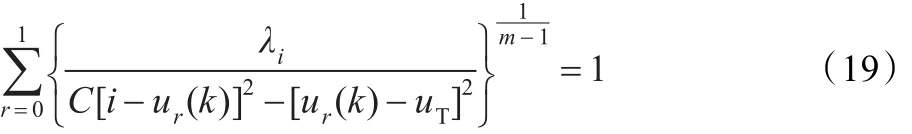
由式（18）、式（19）有：

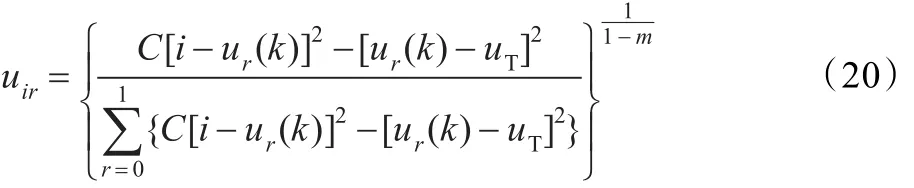
同模糊-C均值聚类算法一致，模糊指数m一般取为2，将像素点硬划分到I0和I1类要求隶属度uir范围在[0，1]，有如下重要结论：

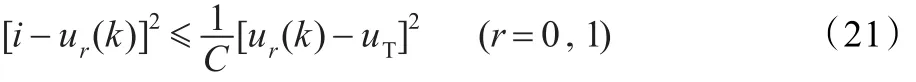
若像素点到图像中类I0(I1)中心的距离为I0和I1两类中心距离的η倍。一般情况下，当η≤1/2时将该像素点硬划分到类I0(I1)较为合理。

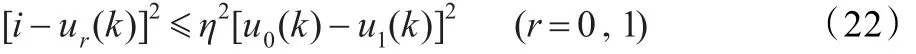
不难发现，当满足式（23）时一定满足硬划分条件：

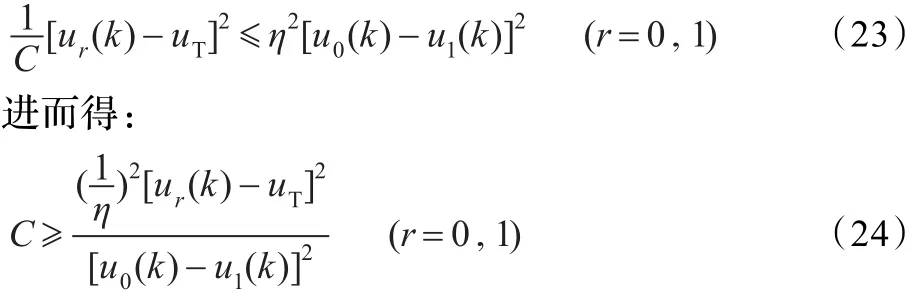
对不同的图像，为了自动地得到一个确切的参数值，取C的值为：

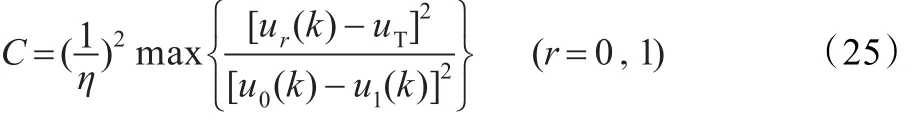
式（25）中uΤ为总体均值。式（25）参数C的取法保证了C的值足够大，完全能满足式（24）的要求，由于参数C的推导是根据拉格朗日数乘法求最大散度差过程中得到的，故得到的参数C的值不会使散度差的最大值发生偏差。当η的值趋于1时，像素点到图像中类I0中心的距离趋于I0和I1两类中心距离，像素点必趋于类I1的中心附近；或像素点到图像中类I1中心的距离趋于I0和I1两类中心距离，像素点必趋于类I0的中心附近，此时η也可视为趋于0，并用式（25）计算对应的参数C的值。通过调节η的取值，可以改变参数C的取值，将C的值代入式（10）中，根据式（11）便可计算得到相应的阈值k。

4 自适应的最大散度差阈值分割法的实现

由参数η的意义，η的值趋近于0或1得到的相应参数C的值较为合理，且考虑边界值1/2和1/4这样的中间值也是有意义的。设定三个η的值，记为(η，η1，η2)，由这三个η值可以得到三个相应的参数C值，记为(C，C1，C2)。由于(C，C1，C2)对应的阈值(k，k1，k2)并不一定是理想的图像分割阈值，借助二分法的迭代思想，不断改变C、C1、C2的值，并根据最大散度差准则计算对应的(k，k1，k2)，AMSD分割法的流程图如图1所示。记|k-k1|为 Δ1；|k-k2|为 Δ2。若Δ1＜Δ2，重新设置：C2←C，C←0.5(C1+C2)，C1的值不改变；当 Δ1＞Δ2时，重新设置：C1←C，C←0.5(C1+C2)，C2的值不改变。再次计算参数(C，C1，C2)对应的(k，k1，k2)，直到 Δ1或 Δ2的值为零，即调整参数C的取值而获得阈值不再改变，可以认为此时参数C对应的k就是最佳的分割阈值。

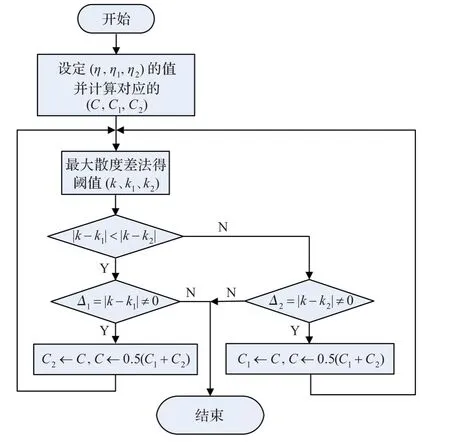
图1 AMSD分割法流程图

AMSD分割法实现的具体步骤：

（1）由图像的灰度直方图得到像素的灰度概率分布pi(i=1，2，…，L-1)。

（2）分别计算隶属于I0和I1两类的p0(k)、p1(k)和u0(k)、u1(k)(k=1，2，…，L-1)，并计算总体均值uΤ。

（3）设定(η，η1，η2)的值，并按式（25）计算(η，η1，η2)对应的(C，C1，C2)。

（4）按照公式（5）～（10）计算散度差，由式（11）得到近似的最优阈值(k，k1，k2)。

（5）比较 Δ1和 Δ2的大小，当 Δ1和 Δ2均大于1时，若Δ1＜Δ2，重置C2←C，C←0.5(C1+C2)，C1的值不变；若Δ1＞Δ2，重置C1←C，C←0.5(C1+C2)，C2的值不改变。

（6）返回步骤（4），直到出现Δ1=0或Δ2=0，取此时的k值为图像分割的最佳分割阈值k*。

（7）在图像中将像素灰度值小于k*置为0，其余像素灰度值置为1，算法结束。

5 实验结果与分析

仿真实验在Τ6570，1 GB内存的笔记本电脑上使用Matlab7.4.0完成，将AMSD分割法分别与传统Otsu法、Fisher准则法对比。对于目标和背景面积相差不大的图像，(η，η1，η2)取为（1/4，1/16，1/2），以调大参数C从而增强类内方差在分离性中的作用；对于目标和背景面积相差较大的图像，(η，η1，η2)取为（1/4，1，1/2），以减小参数C从而减弱类内方差在分离性中的作用。对于用传统Otsu法分割得不到理想效果的图像，用AMSD分割法得到了较好的分割效果，为了说明这一点，选取大小为122×145的帆船图像、大小为308×242的硬币图像和大小为272×280的电路图像进行实验，并设置(η，η1，η2)的值为（1/4，1，1/2）。

图2～4分别为对帆船图像、硬币图像和电路图像的分割效果图。图2（b）中，传统Otsu法没有将帆船底部与水面分开，包含大量虚假信息，Fisher准则法分割结果（见图2（c））相对于Otsu分割法有所改善，但与AMSD分割效果（见图2（d））比较还是有很多误分割的地方；图3（b）、图3（c）显示传统Otsu法、Fisher准则法分割硬币图像时丢失了部分目标信息，而图3（d）中AMSD分割法保留了硬币上许多目标的细节部分；图4（b）中，传统Otsu法没有将距离较近的电路连线分离开来，丢失了轮廓信息，图4（c）中Fisher准则法虽然很好地分离开了不同的布线，但分离出的布线不连续，从图4（d）可以看出，AMSD分割法不但能将电路布线分离开来，还保留了较好的轮廓细节。表1给出了实验所得的分割阈值和处理时间，由于AMSD分割法增加了阈值的搜寻次数和类内方差的计算，略慢于传统Otsu法、Fisher准则法，但完全能够用于实际应用中。

图2 帆船图像的分割效果对比

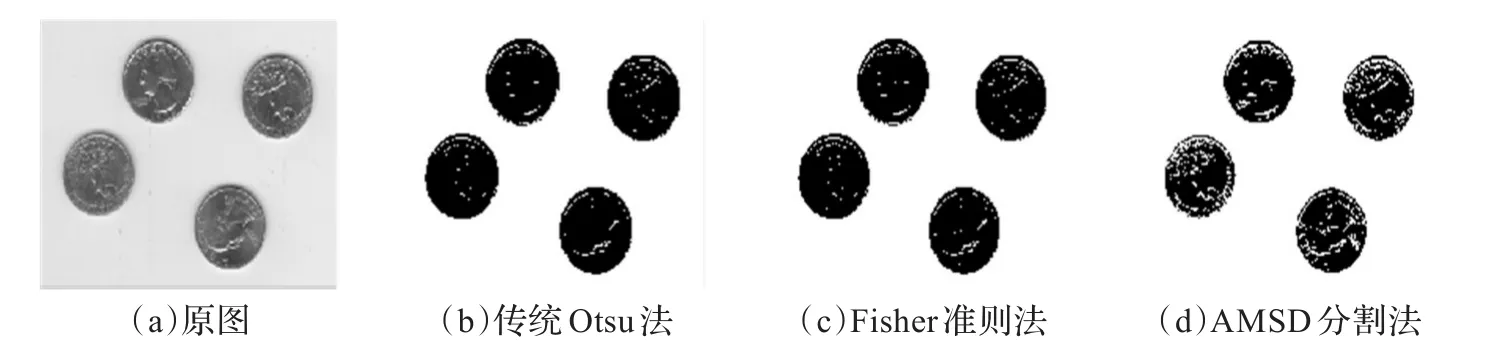
图3 硬币图像的分割效果对比

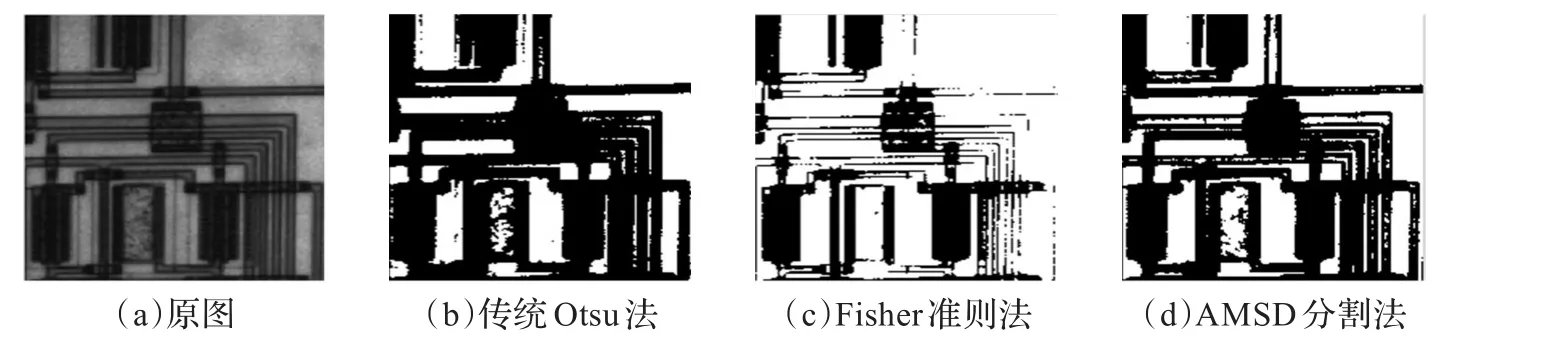
图4 电路图像的分割效果对比

表1 传统Otsu法、Fisher准则法与AMSD分割法图像分割阈值和时间

6 结论

最大散度差准则同时考虑了类间方差和类内方差，提出的AMSD分割法能够自适应地优化参数C的取值和对应的分割阈值，通过与传统算法的比较，证明了AMSD分割法能更好地保留图像中的细节部分，对目标和背景面积相差较大的帆船图像也有较好的分割效果。由于增加了类内方差的计算和阈值的搜寻次数，分割速度略慢于传统算法，但完全能够满足实时应用系统的要求，进一步提高AMSD分割法的处理速度将是下一步要研究的内容。

[1]Otsu N.A threshold selection method from gray-level histogram[J].IEEE Τrans on Systems，Man and Cybernetic，1979，9：62-66.

[2]刘健庄，粟文青.灰度图像的二维Otsu自动阈值分割法[J].自动化学报，1993，19（1）：101-105.

[3]景晓军，蔡安妮，孙景鳌.一种基于二维最大类间方差的图像分割算法[J].通信学报，2001，22（4）：71-76.

[4]孙光灵，周庆松，方传刚.基于最小类内方差的快速阈值分割算法[J].安徽理工大学学报，2005，25（1）：39-42.

[5]吴一全，吴文怡，潘喆.基于二维直方图斜分的最小类内方差阈值分割[J].仪器仪表学报，2007，29（12）：2644-2655.

[6]陈果.图像阈值分割的Fisher准则函数法[J].仪器仪表学报，2003，24（6）：564-567.

[7]宋枫溪，程科，杨静宇.最大散度差和大间距线性投影与支持向量机[J].自动化学报，2004，30（6）：890-896.

[8]王志斌，谷越，李志全.基于最大散度差准则的阈值图像分割[J].应用光学，2010，31（3）：404-405.

[9]皋军，王士同.基于模糊最大散度差判别准则的聚类方法[J].软件学报，2009，20（11）：2939-2949.

[10]支晓斌，范九伦.基于模糊最大散度差判别准则的自适应特征提取模糊聚类算法[J].电子学报，2011，39（6）：1360-1361.

ZHU Gui1,YANG Huixian1,YUE Xuyao1,LENG Ailian2,HE Yali1

1.Department of Photoelectric Engineering,Xiangtan University,Xiangtan,Hunan 411105,China
2.Energy Engineering College,Xiangtan University,Xiangtan,Hunan 411105,China

Aiming at the uncertainty of parameterCin Maximum Scatter Difference（MSD）criterion applied in image segmentation,a preliminary formula is derived with fuzzy concept to calculateC,then optimizeCadaptively based on dichotomy iterative,and the threshold obtained by MSD segmentation accordingly is optimized to a best value.Experimental results show that the Adaptive MSD（AMSD）segmentation can not only make the regions of the segmented image more uniform,but also keep the image details better.

maximum scatter difference;image segmentation;fuzzy;adaptive

针对最大散度差准则运用到图像分割时存在参数C不确定的问题，借助模糊概念导出参数C的初步计算公式，用二分法的迭代思想自适应地优化参数C，使最大散度差分割法获得的分割阈值相应地优化到最佳。实验证明自适应的最大散度差阈值分割法能使分割后的图像区域更均匀、细节保留得更好。

最大散度差；图像分割；模糊；自适应

A

ΤN911.73

10.3778/j.issn.1002-8331.1111-0470

ZHU Gui,YANG Huixian,YUE Xuyao,et al.Thresholding image segmentation based on adaptive maximum scatter difference.Computer Engineering and Applications,2013,49（15）：188-191.

湖南省教育厅资助科研项目（No.10C1263）；湘潭大学资助科研项目（No.11QDZ11）。

祝贵（1986—），男，硕士研究生，主要研究方向：数字图像处理、模式识别；杨恢先（1963—），男，教授，主要研究方向：图像处理、人工智能；岳许要（1984—），男，硕士研究生，主要研究方向：模式识别、人工智能。E-mail：zhugui1218@126.com

2011-11-25

2012-02-03

1002-8331（2013）15-0188-04

CNKI出版日期：2012-04-25 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120425.1719.027.html