月球撞击坑边缘清晰度评价方法的研究

都 骏，苗 放，鲁宇航，唐中林，李 淼

成都理工大学 地球探测与信息技术教育部重点实验室，成都 610059

月球撞击坑边缘清晰度评价方法的研究

都 骏，苗 放，鲁宇航，唐中林，李 淼

成都理工大学 地球探测与信息技术教育部重点实验室，成都 610059

1 引言

2007年10月24日18时05分04秒，我国第一颗探月卫星——“嫦娥一号”（“CE-1”）在西昌卫星发射中心成功发射升空。在随后不到一年的时间内，“嫦娥一号”卫星CCD相机共获得508轨南北纬70°以内和589轨南北纬70°～90°极区的全月球影像数据，第一次实现了对月球表面的100%覆盖[1]。“嫦娥一号”的CCD影像提供了大量关于月表形貌的信息，而撞击坑无疑是最为明显的特征之一。撞击坑能够为研究月球撞击坑历史和演化提供有用信息[2-4]，因此有必要为描述月球撞击坑的影像和几何特征建立模型与标准。提出一种“六位数字十级分级法”，以0至9共十个数字量化描述撞击坑的特征。这六位数字分别是边缘清晰度、直径大小、边缘连续度与圆规则度、坑壁宽度半径比、坑底结构复杂度以及坑底的高程信息。其中，对边缘清晰度的判定能为研究月球撞击坑的风化程度、月表形态特征、进行边缘自动提取等提供科学依据，因而在这六种指标中占有重要地位。本文即是研究边缘清晰度评价的模型建立与评价算法。

2 基本思路

2.1 算法综述

目前国内外并没有关于边缘清晰度的准确定义，现有工作主要集中在对图像清晰度的探讨，尤其是对于相机镜头自动对焦技术的研究比较多。常用的调焦评价函数有灰度差分绝对值之和（SMD）、Laplacian函数、ΤenenGrad函数、基于图像变换的函数等[5-8]。本文提出一种基于图像清晰度评价的边缘清晰度判定算法，该方法首先在边缘上进行点采样开窗、对每个小窗口运用图像清晰度评价算法进行判定，然后综合各窗口的评价结果作为整个撞击坑边缘的清晰度评价结果。在评价算法的选择上，选取基于Sobel算子的空域评价算法、小波变换的频域评价算法以及信息熵的评价算法。最后，运用标准撞击坑的数据对BP神经网络进行训练，将三种算法的评价结果作为网络的输入，得到最终的清晰度量化评价等级，工作思路框架如图1。

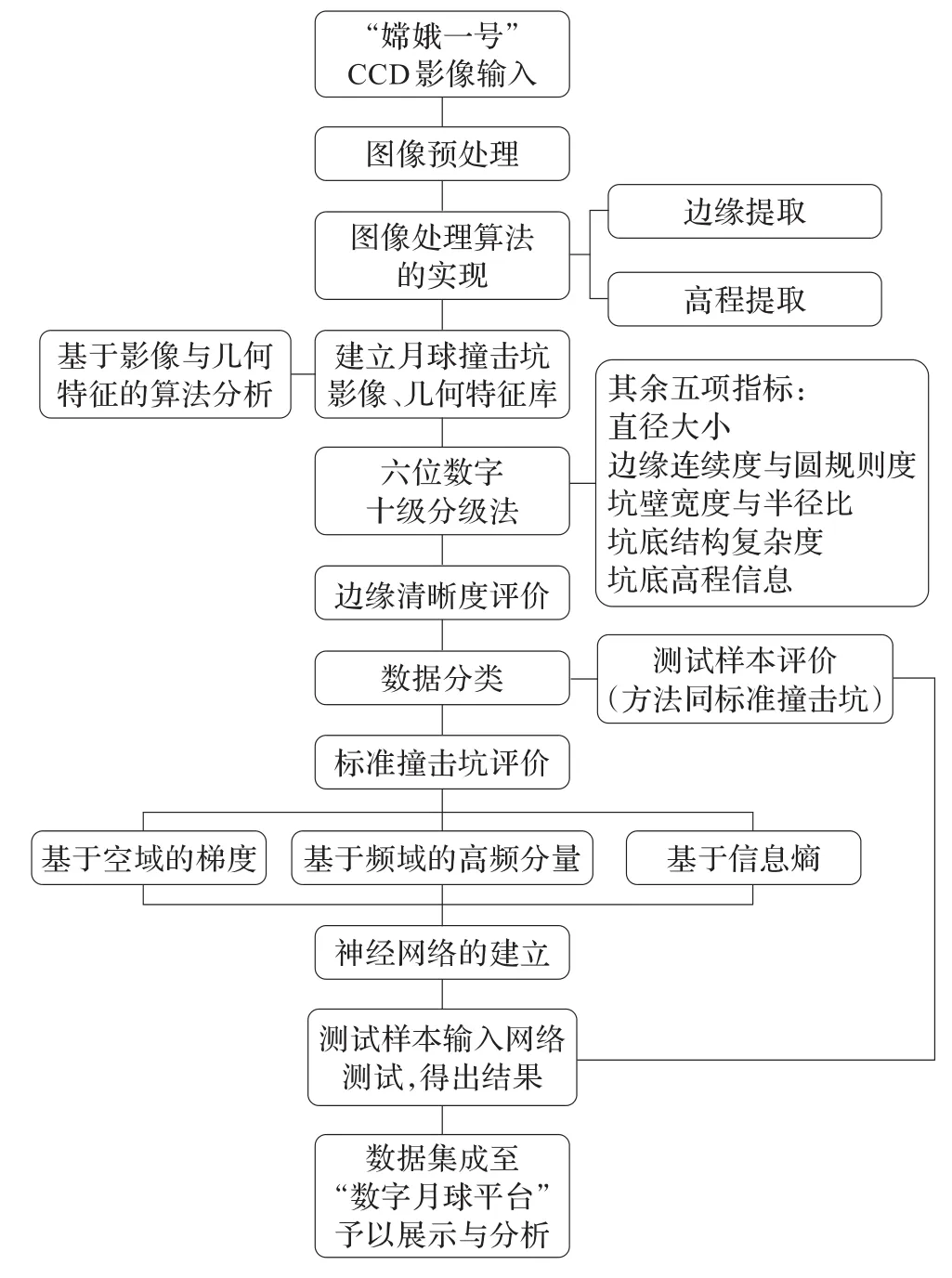
图1 工作思路框架图

2.2 边缘清晰度的定义

边缘清晰度的定义应从空域、频域和信息论三方面入手。具体而言，边缘清晰度可被分别定义为：空域上灰度值的梯度大小，频域上高频成分的含量多少，信息论中信息熵的大小。梯度越大、高频分量越多、信息熵越小，边缘就越清晰。以“六位数字十级分级法”的角度出发，从定性来看边缘清晰度分为三级：模糊、一般、清晰；从定量来看，分为0至9级，清晰度逐渐提升。

2.3 采样开窗法

采样开窗法旨在将图像清晰度评价运用在边缘清晰度评价中。从微观上看，所开的窗口可以当做小幅图像进行清晰度评价；从宏观上看，因为窗口较小，因此可以认为评价结果只反映了窗口中心点附近的清晰度，而不是整个图像的清晰度。边缘是由点组成的，考虑到若对边缘上所有的点进行开窗，算法复杂度与计算时间都会比较大，而且相邻点的空间相关性较高，因此可以在边缘上进行点采样。选择八方向采样的原因是：数字图像阵列表现为二维数组，在二维数组中存在三个方向：水平、垂直、对角线，正好对应在圆周上每隔45°取一个点。而无论是已知中心点想要遍历邻近的8个点还是已知圆上8个点后遍历各点法线方向上的各像素，都只需将其索引加减1或0便可，这为以后的编程提供了方便。采样开窗的示意图见图2。

图2 采样开窗示意图（以Sobel窗口为例）

值得注意的是，由于太阳高度角、CCD镜头拍摄角度等原因，撞击坑内经常会出现高亮与阴影区，二者往往相伴存在并且重心之间的连线与太阳光入射矢量基本保持平行。尤其是在一些小型撞击坑内，由于半径较小，在太阳高度角接近0°时，会出现大面积的高亮与阴影区，几乎占到坑底一半的面积并覆盖大部分坑壁，见图3（a）。因为高亮区和阴影区并未真实反映坑内的地质特征，因此在开窗时可以只向外开窗而不向内开窗，见图3（b）。判定边缘处采样点位于大面积高亮阴影区的方法是，向内法线方向搜索，如果搜索长度内的像素灰度值均大于阈值220或小于阈值30，即认为该点应向外开窗。搜索长度宜定在半径长度的30%左右，或大致覆盖坑壁。

图3 高亮与阴影区的处理示意图

3 边缘清晰度评价算法

3.1 基于Sobel算子的空域评价算法

Sobel算子原是边缘检测中的一个常用算子，它包括两个3×3的方向模板，通过遍历图像中的每个点并与之进行邻域卷积，分别求出该点在水平和垂直方向上的灰度的方向导数，然后通过设定阈值来判断该点是否为边缘点。同样，可以用方向导数值作为撞击坑边缘清晰度的评价指标。考虑到大部分撞击坑都近似圆形且具有对称性，引入一种八方向Sobel算子来处理圆形边缘[9]，它包含八个方向模板以分别用来处理八个方向上的像元，记为t0～t7。模板如下所示：

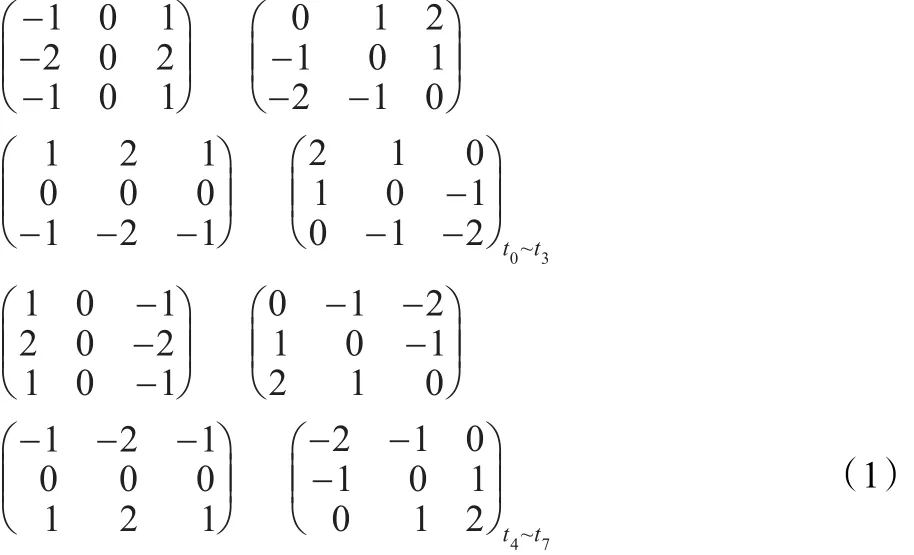
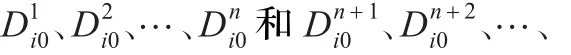
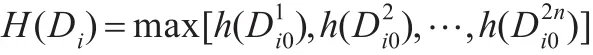
作为撞击坑在ODi0方向上的方向导数。最后，综合八个方向的方向导数作为撞击坑边缘清晰度的评价值F：

3.2 基于小波变换的频域评价算法

小波变换结合能量函数是构造数字图像清晰度评价函数的研究方向之一[10]。小波变换是一种时频分析手段，并且具有多分辨率的特点。图像处理对应的是二维小波变换，其基本原理如下：

由一维的尺度函数ϕ(x)与一维的小波函数ψ(x)可构成一个可分离的二维尺度函数与三个可分离的二维小波函数：

在数字图像处理中需要将上述四式离散化：

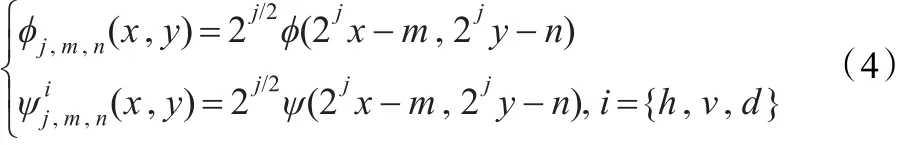
则对于第j层小波变换，可以写成内积的形式：

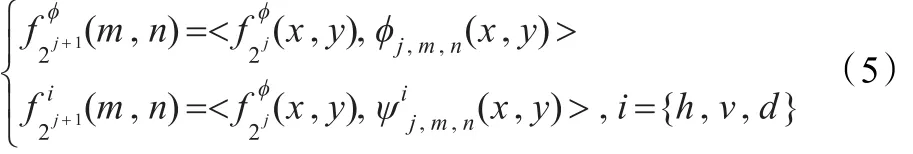
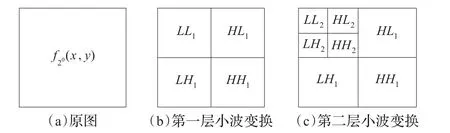
图4 小波变换两层分解示意图

3.3 基于熵的信息论评价算法

月球遥感图像可以被理解为一种光的能量的分布。设一景图像为一张二维网格，拍照时光量子会以某种概率分布的形式进入到网格中。如果某个网格中的光量子越积越多，那么在灰度值上反映为越接近255（8位BMP图像），在概率论上反映为光量子到达的概率越大。

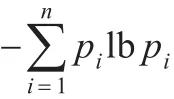
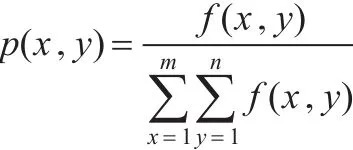
f(x，y)为某点灰度值。所以可以得到基于信息熵的评价函数为：

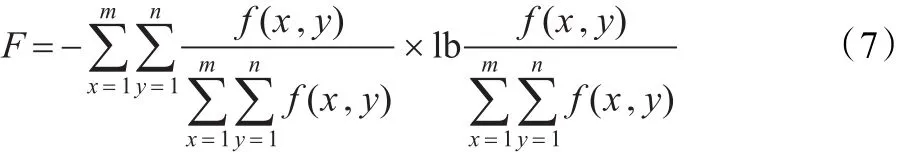
对F的研究是多元函数在约束条件下取极值的问题，可由拉格朗日乘子法解决。经过推导易知，当p1=p2=p3=…=pi=…=pm×n时，F取最大值，对应的情况就是每点的灰度值相同；而当pi=1，pj=0(j=1，2，…，m×n，j≠i)时，F取最小值。因此有推论：图像越模糊，灰度值就越接近均匀分布，信息熵便越大，反之亦然。

3.4 算法的可行性验证与误差分析

为了验证上述三种算法的可行性，共选取50幅撞击坑图像进行测试。分别对每个撞击坑进行两次模糊化处理后，再用以上三种算法进行评价，比较算法的评级结果与客观模糊等级是否一致。由评价函数可知，随着图像由清晰变模糊，Sobel算子与小波变换的评价结果严格单调递减，信息熵的评价结果严格单调递增。如果三幅具有不同清晰度的图像的算法评价结果并未严格单调，便认为算法出现误差。测试数据结果见表1。

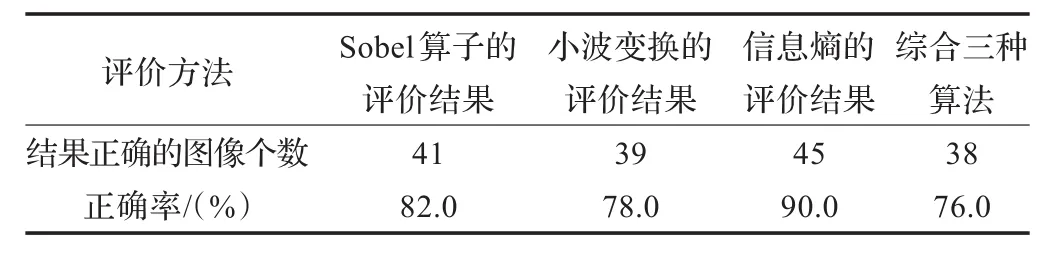
表1 算法验证结果

对于每一幅撞击坑图像，对其人为加噪，并用三种不同方法评价后，不能保证这三种方法的评价值都严格单调。有可能只有两种方法的评价值是单调的，而另一种评价值不单调，因此，三种方法都正确的比例必定小于每一种方法的正确率。本实验中，小波变换的正确率最小，共39幅正确，而这39幅图像中又有1幅的Sobel算子评价值不是单调的，而其他38幅图像的三种评价值均单调，因而综合三种方法都正确的图像的数目为38幅。从验证结果来看，三种评价方法均满足严格单调的图像比例达到76.0%，其中信息熵的评价正确率较高，而小波变换的正确率较低。从人眼视觉角度出发，一幅图像的清晰与否主要还是一种宏观感受，而在边缘点采样所取的结构元素中，由于受各清晰度等级影像中事物灰度值连续的普遍存在性以及所开窗口较小的影响，清晰度不同的图像在某一局部区域的灰度变化剧烈程度实际上并没有整体上大，因此三种评价算法的结果与客观事实存在一定误差。就具体算法而言，因为频率域评价算法是一种变换域评价算法，所关心的是单位距离内灰度值的变化剧烈程度，受所取结构元素较小的影响，在清晰与否的判别上误差较大；而空域与信息熵评价算法主要还是基于对像元灰度值进行分析，因而与视觉评价结果较为一致、误差更小。

4 基于神经网络的清晰度等级判定

前文所述的三种评价方法从不同方面对同一问题进行了研究，但如果考虑到月球表面形态的复杂性与评价结果的局部误差，如果只是单纯地对三种结果加权求和然后作归一化得出的清晰度等级未免缺乏准确性与说服力并且难以推广[13]。因此，需要建立一种标准的清晰度等级划分模式对待检测样本进行判定。考虑到BP神经网络对复杂非线性映射问题的优良处理能力，设计出一种适应于月球表面特征的神经网络判定算法。

4.1 学习样本的建立

首先以边缘类圆完整、周围地貌起伏不大、坑壁较窄、坑底较平缓、高亮阴影区较少以及三种评价算法结果均严格单调为标准，从前述的50个撞击坑中选取20个作为标准撞击坑，对其进行两次人为模糊处理，分为清晰、一般、模糊3个清晰度等级。用三种评价方法对上述标准撞击坑进行评价，再将不同清晰度等级的撞击坑的评价结果线性内插为10个评价值，对应0到9级。然后，将得到的200个评价值用于建立学习样本P=p(i，j)3×200，再将神经网络的期望输出设置为清晰度等级T=[0,0.1,…，0.9,…，0,0.1,…，0.9]1×200。需要指出的是，神经网络的输入数据应进行归一化。传统的最大最小值法易将数据归一化为传递函数Sigmoid的极小值0和极大值1，导致连接权值应足够大才能使网络的输出值与期望值匹配，进而致使训练次数增多、训练时间延长。为避免这种现象，可以通过将输入数据规范到[0.15，0.85]区间内来解决，提出如下的改进型归一化公式：

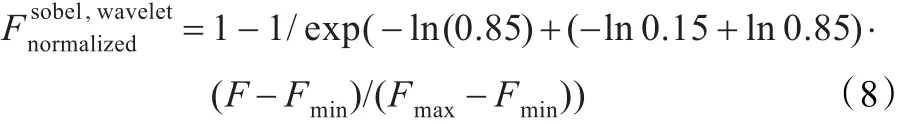
信息熵评价为逆指标，因此归一化公式可改为：

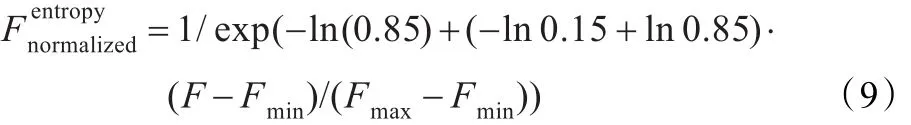
4.2 神经网络的训练

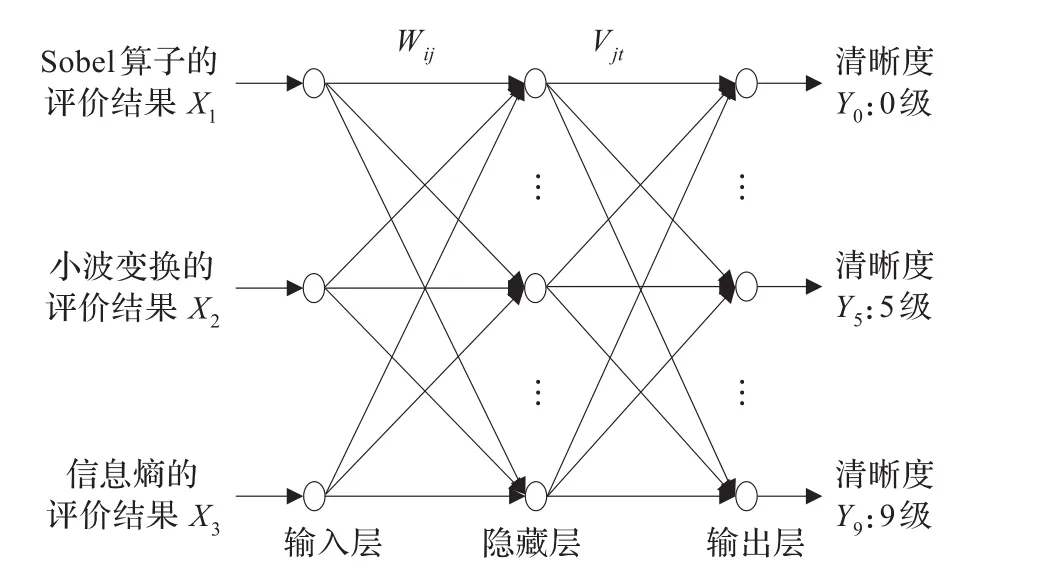
图5 神经网络组合评价示意图

BP神经网络分为三层：输入层、中间层（又称隐含层）和输出层。输入层X1、X2、X3为三种评价算法的值，中间层的各神经元通过Wij(i=1，2，…，n;j=1，2，…，p)与输入层建立权重连接、通过Vjt(j=1，2，…，p;t=1，2，…，q)与输出层建立权重连接。输出层的结果即为最终的评级结果，见图5。由图5可知，神经网络各层单元均与上或下一层各单元建立连接，但每层之间并无连接。神经网络学习的基本步骤为：（1）正向传播：将输入层输入的学习样本通过权值连接送入中间层，经中间层传递函数激活后再通过连接权重送入输出层，经输出层传递函数激活后得到输出结果。（2）反向调整：BP神经网络是一种前馈型（Back-Propagation）神经网络，定义误差函数E，若E不满足预定精度，则应向中间层、输入层反向传递误差，不断修改连接权重与阈值以减小误差。（3）循环调整：不断调整连接权重与阈值，直至误差函数E满足要求，设置迭代上限以避免学习陷入死循环。神经网络的误差变化曲线如图6（a）所示，在训练了746步后，神经网络的输出误差开始小于误差上限0.001。为了检测神经网络的准确性，再次将学习样本输入网络进行检验，得到的误差散点图见图6（b）。由图可知，清晰度评价等级的检验误差基本上都小于0.1，可见神经网络的准确性得到了较高保证。

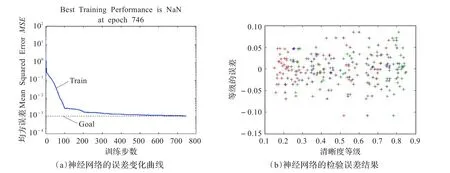
图6 神经网络的训练结果

4.3 评价结果的输出与展示

实验所选取的测试集为20个类圆型撞击坑。为了使判定结果能够与主观判断相互印证，从中选取10幅在主观上即可判断清晰与否的图像予以展示，相关数据见图7、表2。表2神经网络测试结果一栏中的评价结果即对应清晰度评价等级，评价值属于[0，0.05）范围内对应的清晰度等级为0级，评价值属于[0.05，0.15）范围内对应的清晰度等级为1级，以此类推。将所得结果加载到数字月球平台上，可进行全月性的统一展示与分析，见图8。

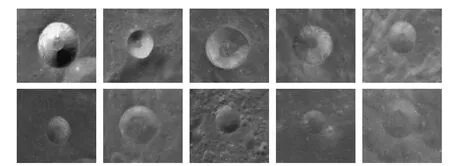
图7 测试图像集（由左至右，由上至下逐渐模糊）

5 结语

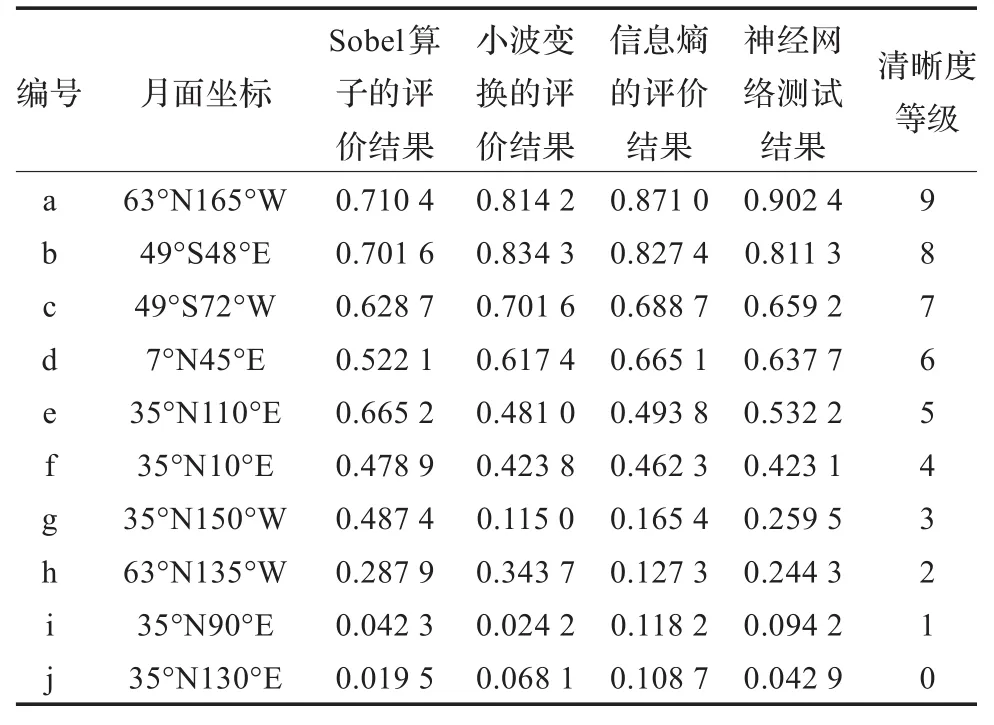
表2 测试集的结果

图8 数字月球平台示意图

本文提出一种基于图像清晰度评价算法的撞击坑边缘清晰度评价算法，用BP神经网络综合处理空域、频域和信息论三方面的评价结果，进而得到最终的清晰度等级。文中以标准撞击坑为基础，通过前述算法建立了撞击坑边缘清晰度评价模型，并对测试样本进行了评价。边缘清晰度评价结果可与其他五项指标一起，为月球表面的撞击坑建立全月性的标准的影像与几何特征库，为探月工程后续工作的展开提供帮助。

[1]欧阳自远，李春来，邹永廖，等.嫦娥一号的初步科学成果[J].自然杂志，2010，32（5）：249-254.

[2]Neukum G，Konig B，Arkani J H.A study of lunar impact crater size-distributions[J].Moon，1975，12：201-229.

[3]Wilhelms D.Τhe geologic history of the moon[R].U.S.Geological Survey Professional Paper 1384，1987.

[4]Gallant J，Gladman B.Lunar cratering asymmetries[C]//Lunar Planet Sci，2006.

[5]Yao Yi，Abidi B，Doggaz N，et al.Evaluation of sharpness measures and search algorithms for the auto-focusing of high magnification images[C]//Visual Information Processing，2006，6246：1-12.

[6]Chen Chihyung，Hwang R，Chen Yuju.A passive anto-focus camera control system[J].Applied Soft Computing，2010，10：296-303.

[7]Kehtarnavaza N，Oh H J.Development and real-time implementation of a rule-based auto-focus algorithm[J].Real-time Imaging，2003，9：197-203.

[8]Meng Bo，Zhu Ming，Cai Changjin.Design of video auto focusing based on image processing[C]//Optical Information Processing，2006，6027：501-509.

[9]蒋婷，谭跃刚，刘泉.基于Sobel算子的图像清晰度评价函数研究[J].计算机与数字工程，2008，36（8）：129-131.

[10]Al-hudhud G，Ibrahim M K，Al-Akaidi M.Automatic production of quantisation matrices based on perceptual modeling of wavelet coefficients for grey scale images[J].Image and Vision Computing，2010，28：644-653.

[11]刘斌.基于图像技术的自动调焦方法研究与实现[D].杭州：浙江大学，2004.

[12]Wellmann J K，Regenauer-Lieb K.Uncertainties have a meaning：information entropy as a quality measure for 3-D geological models[J].Τectonophysics，2012，526.

[13]Gastaldo P，Zunino R，Heynderickx I，et al.Objective quality assessment of displayed images by using neural networks[J]. Signal Processing：Image Communication，2005，20.

DU Jun,MIAO Fang,LU Yuhang,ΤANG Zhonglin,LI Miao

Key Lab of Earth Exploration&Information Τechniques of Ministry of Education,Chengdu University of Τechnology,Chengdu 610059,China

Impact crater is one of the most important geological structures on the surface of moon.By appraising the edge definition of impact craters in the CCD images of“CE-1”,some geological information can be inverted such as the rate of decay and the undulation of topography.Considering the gradient in spatial domain,the high-frequency component in frequency domain and the theory of information,an algorithm derived from image definition appraisal is presented,aiming at appraising the edge definition of impact craters.Altogether three algorithms are realized,respectively based on Sobel algorithm,wavelet transform and entropy of information.A kind of BP neural network which is adapted to the feature of impact crater is designed and results from different algorithms are combined as the inputs to the network,thus the final rank of the edge definition is achieved.Τhe final results are loaded into the Digital Platform for Moon（DPM）to be displayed and make further analysis.

impact crater;edge definition;appraisal algorithm;Sobel algorithm;wavelet transform;entropy of information; Back Propagation（BP）neural network;Digital Platform for Moon（DPM）

撞击坑是月球表面最重要的地质构造之一，通过对“嫦娥一号”CCD影像中撞击坑的边缘清晰度进行评价，可以进一步反演出月球表面的风化程度、地表起伏等地质信息。提出一种基于图像清晰度评价的边缘清晰度评价方法，从空域的梯度、频域的高频分量以及信息论三个方面，运用基于Sobel算子、小波变换和信息熵的算法对撞击坑的边缘清晰度予以评价。设计出一种适应于月球撞击坑特征的BP神经网络，组合三种评价算法的结果作为其输入，进而得到最终的清晰度等级。将最终结果加载到具有自主知识产权的数字月球平台上予以全月性的展示和进一步分析。

撞击坑；边缘清晰度；评价算法；Sobel算子；小波变换；信息熵；反向传播（BP）神经网络；数字月球平台

A

ΤP751.1

10.3778/j.issn.1002-8331.1111-0435

DU Jun,MIAO Fang,LU Yuhang,et al.Research on appraisal of edge definition of impact craters.Computer Engineering and Applications,2013,49（15）：179-183.

国家高技术研究发展计划（863）（No.2010AA12202）。

都骏（1990—），男，主要研究方向为空间信息与数字技术；苗放（1958—），男，教授，博士生导师，主要研究方向为空间信息技术、计算机网络；鲁宇航（1990—），男，主要研究方向为空间信息与数字技术；唐中林（1989—），男，硕士研究生，主要研究方向为空间信息技术；李淼（1988—），女，硕士研究生，主要研究方向为空间信息技术。E-mail：mf@cdut.edu.cn

2011-11-23

2012-01-04

1002-8331（2013）15-0179-05

CNKI出版日期：2012-04-25 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120425.1719.031.html