图像脉冲噪声检测

罗海驰，李岳阳，孙 俊

江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122

图像脉冲噪声检测

罗海驰，李岳阳，孙 俊

江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122

1 引言

数字图像是由以有限数值表示的像素构成的二维图像，与传统的模拟图像相比，数字图像具有易存储、可加密、处理速度快、复制成本低、传输效率高等优势。目前，数字图像处理技术在地球资源遥感、医学成像、空间探测、刑事侦察、媒体传播等领域均有广泛应用[1]。

数字图像在其获取、传输过程中因种种原因可能导致在正常的图像数据中混入噪声信号。这些噪声信号降低了数字图像的质量，也影响了后续应用的开发[2]。为解决这一问题，相关领域研究人员已提出了许多图像去噪的方法。

图像中一般既有较为平滑的区域，也有丰富的细节或边缘，这些细节或边缘通常包含重要的视觉感知信息。因此，图像滤波的目的除了去除噪声外，还要尽可能地保留细节或边缘等信息[3]。在针对被脉冲噪声污染的图像滤波技术中，非线性滤波的效果要优于线性滤波，因为线性滤波会造成图像的细节和边缘模糊，影响图像的视觉效果[4]。标准中值滤波[5]（SMF）方法是一种经典的非线性滤波方法，它用预先定义的滤波窗口中所有像素的灰度值的中值来替换该窗口中心点像素的灰度值。该方法简洁有效，能很好地滤除图像中的脉冲噪声。为进一步提高SMF的滤波性能，O.Yli-Harja等提出了加权中值滤波器[6]（WMF），S.J.Ko等提出了中心加权中值滤波器[7]（CWMF），这两类滤波器给予滤波窗口内特定的像素更多的权值。

以上这三种滤波器对于噪声图像中所有的像素都采用相同的滤波处理，这就在滤波的同时不可避免地破坏未被噪声污染的像素。因为对于脉冲噪声图像，只是图像中的部分像素会被噪声污染，所以在实际应用中，希望滤波方法仅对噪声像素进行处理，而对非噪声像素则保持不变。因此，在滤波前，可采用一个噪声检测器，把图像中的噪声像素和非噪声像素区分开来。如果一个像素被检测出是噪声像素，它将被中值滤波器的输出替代；反之，该像素保持不变。对于这类开关型中值滤波器，脉冲噪声检测器的性能好坏是至关重要的。基于这一思想，Z.Shuqun等提出了EDMF方法[8]，C.Τao等提出了MSMF方法[9]，W.Zhou等提出了PSMF方法[10]，E.Abreu等提出了SDROMF方法[11]。这些滤波器能较好地检测出图像中的脉冲噪声，但在算法中需确定一些参数的值，而这些参数的最优值的确定，是一个比较困难的问题。

在噪声图像中，细节或边缘与噪声之间的区别并不明显。这种信息的不确定性和不完整性给滤波操作带来了困难，而模糊理论正好能适应这些非确定性，因此在图像滤波过程中应用模糊理论可以取得较好的噪声去除效果。F.Russo等将模糊系统理论应用于图像滤波，提出了FF方法[12]。人工神经网络方法与传统方法相比表现出很大的优越性，人工神经网络具有高度并行处理能力，具有自学习、自组织能力，能够根据学习样本找出输入与输出数据之间的内在联系，具有非线性映射功能，特别适合图像处理中许多非线性问题。近年来，神经模糊理论综合了模糊理论模拟滤波过程中的不确定性的能力和人工神经网络强大的学习能力，逐渐应用在图像的滤波[13-15]中。

在本文中，提出了一个包含两个自适应神经模糊推理系统和一个后处理块的网络，用于检测灰度图像中的椒盐脉冲噪声，并用该噪声检测器与中值滤波器配合，对测试图像进行滤波。网络中每个自适应神经模糊推理系统都是一个四输入单输出一阶Sugeno模糊推理系统[16]。所提出的噪声检测方法分两步进行，在使用该网络对噪声图像进行噪声检测前，首先人工构造一个训练图像，使用混合学习算法[16]对两个自适应神经模糊推理系统分别单独进行训练，确定系统中的参数；当两个自适应神经模糊推理系统都训练完毕，就可以和一个后处理块一起构成网络，对测试图像进行噪声检测。

2 噪声检测算法

2.1 神经模糊网络

图1是包含两个自适应神经模糊推理系统和一个后处理块的网络结构图。每个自适应神经模糊推理系统都是一个四输入单输出一阶Sugeno模糊推理系统。每个自适应神经模糊推理系统对应一个数据提取块。每个数据提取块为相应的自适应神经模糊推理系统提供四个输入。数据提取的具体步骤如下：

（1）如图2所示，以当前操作像素p2为中心，得到一个3×3滤波窗口，依照水平和垂直二种不同的拓扑结构得到像素灰度值p1、p2和p3。

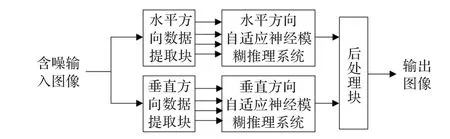
图1 自适应神经模糊推理系统网络结构图

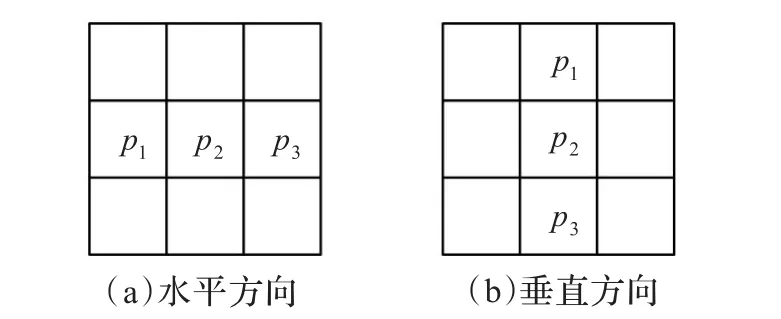
图2 两个数据提取块所对应的拓扑结构

（2）仍以当前操作像素p2为中心，另外得到一个预先定义的中值提取操作窗口，由该窗口内所有像素点的灰度值，得到中值m，中值提取操作窗口大小的确定将在第3章中详细介绍。

（3）令每个自适应神经模糊推理系统的四个输入x1、x2、x3和x4分别为：

2.2 自适应神经模糊推理系统

图1中两个自适应神经模糊推理系统的内部结构都相同，都是一个四输入单输出一阶Sugeno模糊推理系统。对于输入图像中的当前操作像素，根据2.1节，每个数据提取块为相应的自适应神经模糊推理系统提供四个输入x1、x2、x3和x4。对于每个输入，分别定义三个广义钟型隶属函数，则每个自适应神经模糊推理系统包含81（即34）条规则，其模糊规则集如下：

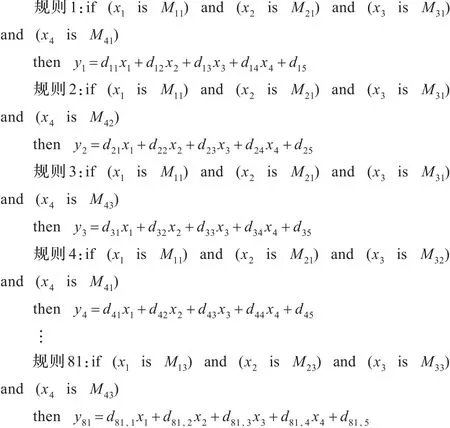
其中Mij表示第i个输入的第j个隶属函数，dkl为结论参数，yk为系统根据第k个规则得到的输出，i=1，2，3，4，j=1，2，3，k=1，2，…，81，l=1，2，3，4，5。对于输入xi，定义的广义钟型隶属函数为：

其中aij，bij和cij为前提参数，i=1，2，3，4，j=1，2，3。

自适应神经模糊推理系统的输出Y等于各yk的加权平均：

式中加权系数wk表示第k条规则的激励强度，wk的计算公式如下：

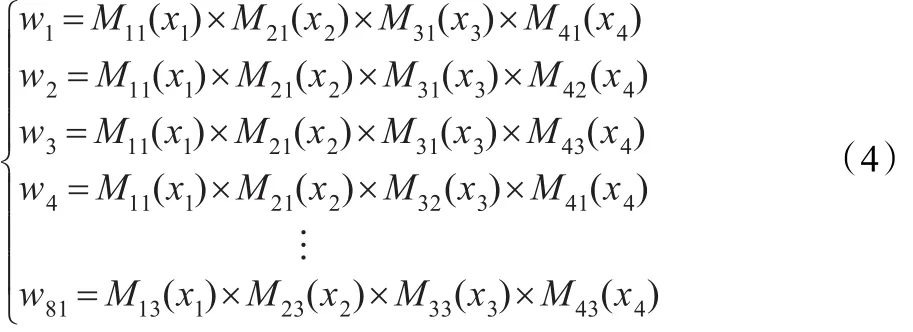
每个自适应神经模糊推理系统中的前提参数aij，bij，cij和结论参数dkl都需要通过训练确定其值，系统进行训练时所使用的优化算法为混合学习算法[16]，即前提参数aij，bij和cij通过梯度法进行优化，结论参数dkl通过线性最小二乘法进行优化，这样可大大提高优化速度，提高学习效率。

图1中由两个自适应神经模糊推理系统可分别得到两个输出，记为Yk(k=1，2)。这两个输出即为后处理块的输入。后处理块按式（5）对这两个输入取平均值，记为YF，再按式（6）求得神经模糊网络的最终输出Y，该值为1表示当前操作像素是噪声点，为0表示当前操作像素不是噪声点。

2.3 混合学习算法

在本文中，采用混合学习算法[16]对自适应神经模糊推理系统中的参数进行优化，即前提参数aij，bij和cij通过梯度法进行优化，结论参数dkl用线性最小二乘法进行优化，采用的学习策略为离线（批量）学习法。

假设有N组训练数据，对于每一组输入xt=(x1，x2，x3，x4)Τ，系统的实际输出和期望输出分别为Yt和Ydt，t= 1，2，…，N，Τ表示矩阵转置，定义代价函数：

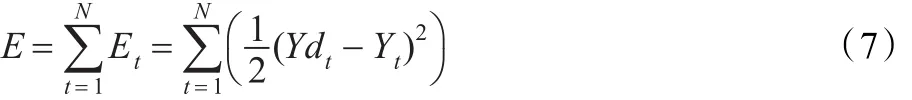
对于前提参数aij，bij，cij，根据梯度法有：

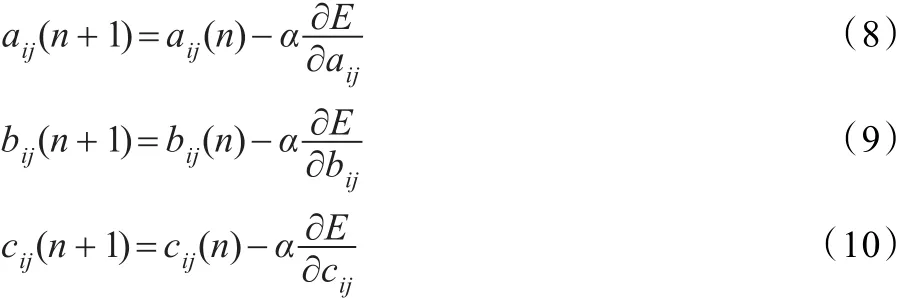
其中n为迭代次数，α为学习速率，i=1,2,3,4，j=1,2,3。训练时，可以根据N组训练数据来确定前提参数aij，bij和cij的初始值。

对于结论参数dkl，首先根据前提参数的初始值、式（3）和N组训练数据（包括输入和期望输出），采用线性最小二乘方法来确定其初始值，然后由式（3）求得N组训练数据的系统实际输出，再根据式（7）的代价函数以及式（8）～（10）来更新前提参数aij，bij和cij，并在每次更新前提参数之后，采用线性最小二乘方法更新结论参数dkl。这样一直迭代下去，直到式（7）的代价函数值小于预先设定的阈值或者迭代次数达到预先设定的上限时，则系统训练结束。

2.4 训练过程

在使用图1所示网络对测试图像进行噪声检测前，每个自适应神经模糊推理系统都需单独进行训练，确定前提参数aij，bij，cij和结论参数dkl的值。图3是单个自适应神经模糊推理系统训练优化过程图。训练图像可通过计算机人工构造得到，每个自适应神经模糊推理系统都采用相同的训练图像。图4（a）是每个自适应神经模糊推理系统的原始训练图像，该图像大小为64×64，是由256个4×4色块组成，每个色块中的16个像素具有相同的灰度值，不同色块的灰度值各不相同，256个色块的灰度值遍取0到255中的所有值，不同灰度值的色块在图像中的位置是随机的。图4（b）是系统的输入的训练图像，是在图4（a）上添加30%的椒盐脉冲噪声得到的噪声图像。图4（c）是系统期望输出的训练图像。若图4（a）中像素点与图4（b）中对应位置像素点的灰度值的差为0，则图4（c）中相应像素点的值为0，显示为黑色，表示图4（b）中该点不是噪声点；若图4（a）中像素点与图4（b）中对应位置像素点的灰度值的差不为0，则图4（c）中相应像素点的值为1，显示为白色，表示图4（b）中该点是噪声点。在仿真实验中，为测试所提出的网络的噪声检测效果，分别对8张原始图像添加3%～80%椒盐脉冲噪声。由仿真实验可知，采用计算机人工构造的图像训练后的网络，对于图像噪声检测具有鲁棒性，即测试图像与训练图像可完全不同，且训练图像中的噪声密度也无需与测试图像中的噪声密度相同，也就是说，该训练后的网络对受不同噪声密度污染的各类图像噪声检测效果都较好。

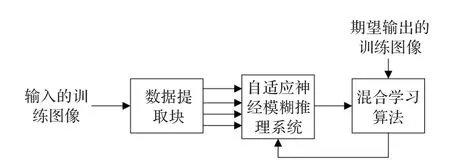
图3 自适应神经模糊推理系统训练优化过程图

图4 人工训练图像

每个自适应神经模糊推理系统中的参数都需要通过训练确定其值，训练过程如下：

（1）对输入的训练图像中的所有像素，按从上到下，从左到右的顺序，逐个进行操作。

（2）对当前操作像素，数据提取块按2.1节中所述方式得到系统的四个输入，再由这四个输入得到系统的一个实际输出。

（3）选取输入的训练图像中下一个像素作为当前操作像素，重复步骤（2），通过这样的方式可得到输入的训练图像中所有像素噪声标志值的系统实际输出。

（4）根据输入的训练图像中所有像素噪声标志值的系统实际输出和由期望输出的训练图像得到的期望输出的差值，得到式（7）的代价函数值，使用2.3节中混合学习算法对系统中的前提参数和结论参数进行更新。

（5）当式（7）的代价函数值小于预先设定的阈值或者迭代次数达到预先设定的上限时，系统训练结束；否则，重复上述步骤，进行下一次迭代训练。

2.5 检测过程

如图1所示，当两个自适应神经模糊推理系统都训练完毕，就可以和一个后处理块一起构成一个网络，对测试图像进行噪声检测。

检测过程如下：

（1）以测试图像为输入图像，对其中所有像素，按从上到下，从左到右的顺序，逐个进行操作。

（2）对当前操作像素，两个数据提取块分别按2.1节中所述方式得到相应系统的四个输入。

（3）每个自适应神经模糊推理系统都会得到一个输出，这两个输出即为后处理块的两个输入，后处理块按2.2节中所述方式对这两个输入进行相应处理，得到一最终输出，该输出即为输入图像当前操作像素的噪声标志值（图1中的输出图像）。

（4）选取输入图像中下一个像素作为当前操作像素，重复步骤（2）至（4）。

（5）当输入图像中所有像素经过网络都得到输出后，就能得到一个输出图像，该输出图像即为测试图像对应的噪声标志图像。

2.6 滤波过程

对于测试图像，首先按本文所提方法进行噪声检测，得到与测试图像相对应的噪声标志图像后，然后就可与任何一种噪声滤波器配合对测试图像进行滤波。在本文中，选择中值滤波器，即对标志为噪声的像素以中值滤波结果作为该像素的输出，对标志为非噪声的像素以原值作为该像素的输出。对测试图像进行滤波的过程图如图5所示。

滤波过程如下：

（1）以测试图像为输入图像，按2.5节中所述方式进行噪声检测，得到其对应的噪声标志图像。

图5 图像滤波过程图

（2）对测试图像进行中值滤波得到滤波结果图，滤波窗口大小与噪声检测时所用中值提取操作窗口大小一致，在第3章中将详细介绍。

（3）对噪声标志图像中所有像素，按从上到下，从左到右的顺序，逐个进行操作：若当前操作像素的值为1，则表明测试图像中对应位置的像素点为噪声点，以中值滤波结果作为该像素的输出值；若当前操作像素的值为0，则表明测试图像中对应位置的像素点不是噪声点，以原值作为该像素的输出值。

（4）当噪声标志图像中所有像素都操作完成后，就能得到一个输出图像，该输出图像即为测试图像对应的滤波后图像。

3 实验结果

为测试基于自适应神经模糊推理系统噪声检测方法的性能，将其与传统滤波方法EDMF[8]、MSMF[9]、PSMF[10]、SDROMF[11]和FF[12]的噪声检测及图像滤波能力相比较，对图6中8张图（图像大小都为256×256）进行测试分析。为避免偶然性，更客观地评测各种滤波方法的噪声检测性能，在本文的实验中，首先图6中8张图分别被3%～80%椒盐脉冲噪声污染，以生成一组测试图像，然后将该过程重复十次，生成十组不同的测试图像，最后实验结果取十组测试图像的平均值。

图6 测试图像

在2.1节中，数据提取块为相应的自适应神经模糊推理系统提供四个输入，在选取中值m时，需确定中值提取操作窗口大小。通过对常规中值滤波器的性能分析可知，中值的选取受滤波窗口尺寸的影响较大，它在抑制图像噪声和保护细节这两个方面存在一定的矛盾：若选取的滤波窗口较小，则有利于保护图像中某些细节，但会限制滤噪能力；反之，若选取的滤波窗口较大，则可加强抑噪能力，但对细节的保护能力会减弱。这种矛盾在图像中噪声干扰较大时表现得尤为明显。在本文中，通过仿真实验证明，根据脉冲噪声强度的大小不同，采用表1中方法确定提取操作窗口大小，实验结果为最好。

表1 提取操作窗口大小的选择

3.1 检测性能定量评价

对于采用噪声检测器的滤波方法，检测器的性能好坏是至关重要的，直接影响到最后的滤波效果。在对噪声检测器的检测能力进行测试的过程中，有两种情况需要考虑[13]。第一，有可能有一部分噪声像素被检测器误检为非噪声像素，也就是说这些噪声像素没有被检测器检测出来；第二，也有可能有一部分非噪声像素被检测器误检为噪声像素。为了对噪声检测器的检测能力进行定量评价，分别按式（11）～式（13）计算其漏检率Pu、错检率Pm及总误检率PF。

其中Nu是误将噪声像素判断为非噪声像素的数目，即没有被检测出来的噪声像素数目；Nm是误将非噪声像素判断为噪声像素的数目；Nt是含噪图像的总像素数。

在仿真实验中，为评价本文所提出的噪声检测方法，将其与传统滤波方法EDMF[8]、MSMF[9]、PSMF[10]、SDROMF[11]和FF[12]的噪声检测能力相比较。实验过程描述如下：

（1）对于被同一种噪声密度污染的8张图像，生成十组共80幅测试图像，选择其中一种噪声检测方法，分别计算出80个不同的Pu、Pm及PF值，取平均值作为该种方法在该种噪声密度下的Pu、Pm及PF的代表值。

（2）对于被其他噪声密度污染的图像，采用同样的实验过程，得到该种方法在这些噪声密度下的Pu、Pm及PF的代表值。

（3）对于其他的噪声检测方法，采用上述相同的实验过程，得到这些方法在所有噪声密度下的Pu、Pm及PF的代表值。

图7是各方法对受3%～80%强度椒盐脉冲噪声污染的图像的噪声检测性能对比图，其中图7（a）是漏检率Pu值比较曲线，图7（b）是错检率Pm值比较曲线，图7（c）是总误检率PF值比较曲线。从图中可以明显地看出，对受不同强度椒盐脉冲噪声污染的图像，本文方法得到的漏检率、错检率、总误检率值都小，这说明了该方法的噪声检测能力比其他方法好。

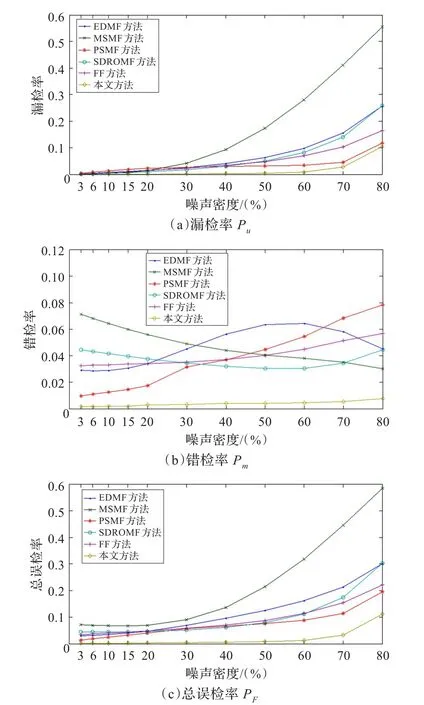
图7 噪声检测性能定量评价对比

3.2 滤波性能定量评价

在实验中，采用平均均方误差MSE，峰值信噪比PSNR评价标准定量评价滤波器的性能。MSE值越小或PSNR值越大表明滤波器滤波效果越好。实验过程描述如下：

（1）对于被同一种噪声密度污染的8张图像，生成10组共80幅测试图像，选择其中一种滤波方法进行滤波，得到使用该种方法滤波后的80个不同的MSE值和PSNR值，取平均值作为该种方法在该种噪声密度下的MSE和PSNR的代表值。

（2）对于被其他噪声密度污染的图像，采用同样的实验过程得到该种方法在这些噪声密度下的MSE和PSNR的代表值。

（3）对于其他滤波方法，进行相同的实验过程，得到这些滤波方法在所有噪声密度下的MSE和PSNR的代表值。

图8（a）和图8（b）分别给出了2.6节所述滤波方法和传统的滤波方法，对受3%～80%强度椒盐脉冲噪声污染的图像滤波后的MSE和PSNR比较曲线。从图中可以明显地看出，对受不同强度椒盐脉冲噪声污染的图像，2.6节中滤波方法得到的MSE都小而PSNR都大，这说明了该方法的滤波效果较传统的滤波方法为好。

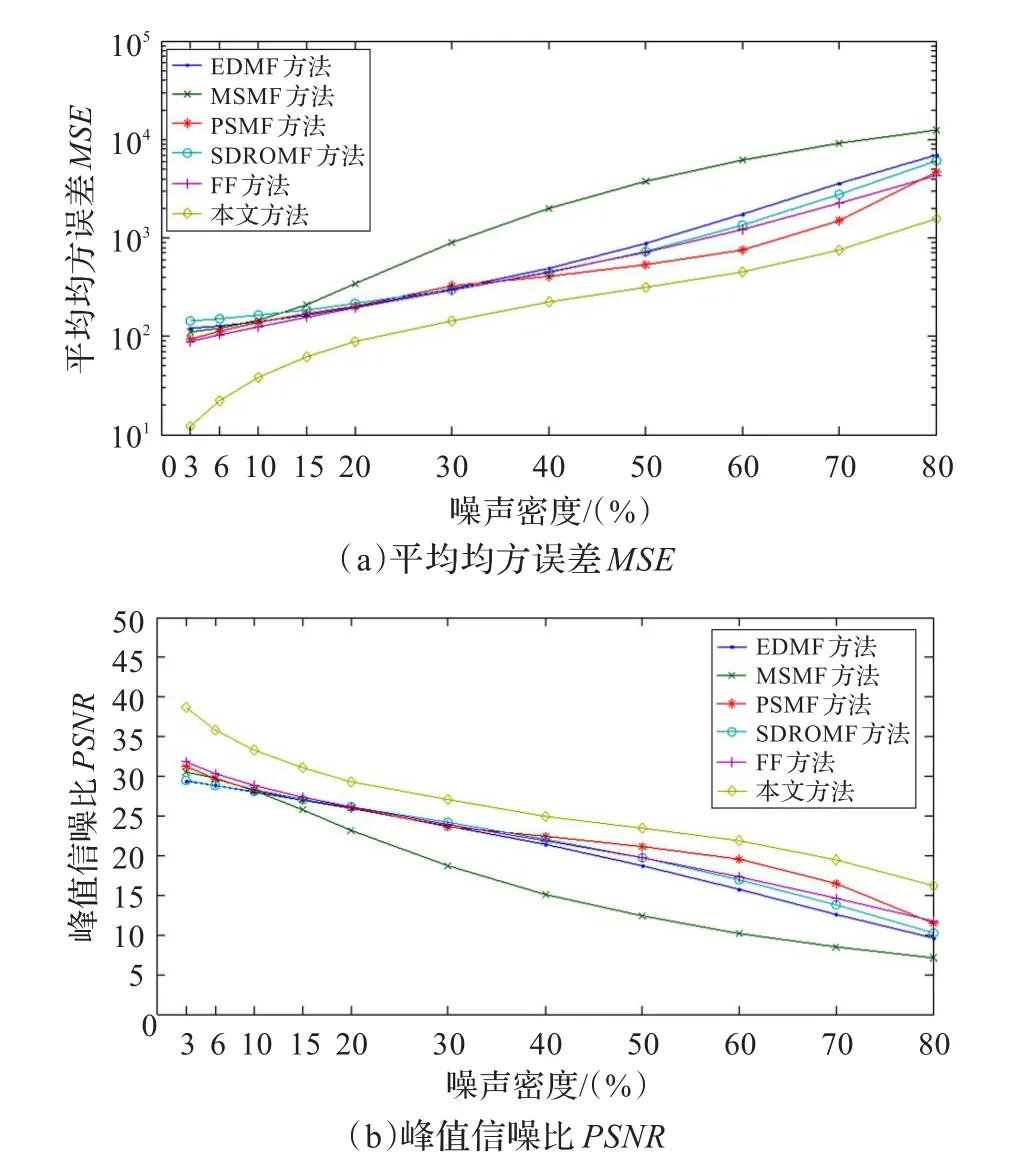
图8 滤波效果定量评价对比

3.3 滤波性能定性评价

对于评价滤波性能，除了上述的定量评价之外，还需进行定性评价。主观的定性评价就是从视觉上观察各种滤波器的滤波效果。图9显示的是测试图像为Baboon图的滤波效果对比图。图9（a）为原始图像（未被噪声污染图像）Baboon图，图9（b）为含30%的椒盐脉冲噪声图，图9（c）～（g）分别为各传统滤波方法所输出的结果图像，图9（h）为2.6节所述滤波方法所输出的结果图像。由这些滤波效果图可以看出，常用的传统滤波方法（EDMF、MSMF、PSMF、SDROMF和FF）的输出图像中，有明显的没有被去除的噪声点，特别是MSMF方法的输出图像中，没有被去除的噪声点很多。而在本文滤波方法的输出图像中，噪声去除得比较干净，这说明，该滤波方法去除脉冲噪声的能力较传统滤波方法为强。另外，与传统滤波方法的输出结果相比，本文滤波方法更能保留原有图像的细节或边缘，这可以从Baboon的眼睛周围和胡须部位可以明显看出。

4 结论

在本文中，提出了一个基于自适应神经模糊推理系统的网络，该网络包含两个自适应神经模糊推理系统和一个后处理块，每个自适应神经模糊推理系统都是一个四输入单输出一阶Sugeno模糊推理系统。该网络可作为一种新的噪声检测方法，用于被椒盐脉冲噪声污染的灰度图像的噪声检测。所提出的新噪声检测方法，有以下一些特点。

（1）不需要确定一些可调参数的值。

（2）在网络的训练过程中，采用混合学习算法，用于提高网络中前提参数和结论参数的更新速度。

（3）训练图像很容易可由计算机人工构造，并由仿真实验可知，采用这样的方法构造的图像训练后的网络，对于噪声检测具有鲁棒性。

由仿真实验结果可以看出，新噪声检测方法的噪声检测能力明显优于传统的滤波方法。

图9 新滤波器和常用滤波器的滤波效果对比图（测试图像Baboon被30%的脉冲噪声污染）

[1]Gonzalez R C，Woods R E.数字图像处理[M].阮秋琦，译.2版.北京：电子工业出版社，2003.

[2]霍宏涛.数字图像处理[M].北京：北京理工大学出版社，2002.

[3]Plataniotis K N，Venetsanopoulos A N.Color image processing and applications[M].Berlin：Springer，2000.

[4]Pitas I，Venetsanopoulos A N.Order statistics in digital image processing[J].Proceedings of the IEEE，1992，80（12）：1893-1921.

[5]Pratt W K.Digital image processing[M].New York：Wiley Interscience，1978.

[6]Yli-Harja O，Astola J，Neuvo Y.Analysis of the properties of median and weighted median filters using threshold logic and stack filter representation[J].IEEE Τransactions on Signal Processing，1991，39（2）：395-410.

[7]Ko S J，Lee Y H.Center weighted median filters and their applications to image enhancement[J].IEEE Τransactions on Circuits and Systems，1991，38（9）：984-993.

[8]Shuqun Z，Karim M A.A new impulse detector for switching median filters[J].Signal Processing Letters，IEEE，2002，9（11）：360-363.

[9]Τao C，Ren W H.Space variant median filters for the restoration of impulse noise corrupted images[J].IEEE Τransactions on Circuits and Systems II：Analog and Digital Signal Processing，2001，48（8）：784-789.

[10]Zhou W，Zhang D.Progressive switching median filter for the removal of impulse noise from highly corrupted images[J]. IEEE Τransactions on Circuits and Systems II：Analog and Digital Signal Processing，1999，46（1）：78-80.

[11]Abreu E，Lightstone M，Mitra S K，et al.A new efficient approach for the removal of impulse noise from highly corrupted images[J].IEEE Τransactions on Image Processing，1996，5（6）：1012-1025.

[12]Russo F，Ramponi G.A fuzzy filter for images corrupted by impulse noise[J].Signal Processing Letters，IEEE，1996，3（6）：168-170.

[13]Li Y，Chung F L，Wang S.A robust neuro-fuzzy network approach to impulse noise filtering for color images[J].Applied Soft Computing，2008，8（2）：872-884.

[14]Yuksel M E，Basturk A.A simple generalized neuro-fuzzy operator for efficient removal of impulse noise from highly corrupted digital images[J].AEU-International Journal of Electronics and Communications，2005，59（1）：1-7.

[15]Li Y，Luo H，Sun J.A neuro-fuzzy network approach to impulse noise filtering[C]//3rd International Workshop on Combinations ofIntelligentMethods and Applications（CIMA2012），2012：19-22.

[16]Jang J S R，Sun C Τ.Neuro-fuzzy and soft computing：a computational approach to learning and machine intelligence[M]. Upper Saddle River，NJ，USA：Prentice-Hall，Inc.，1997.

LUO Haichi,LI Yueyang,SUN Jun

Key Lab ofAdvanced Process Control for Light Industry（Ministry of Education）,Jiangnan University,Wuxi,Jiangsu 214122,China

A neuro-fuzzy network approach to impulse noise detection for gray scale images is presented.Τhe network is constructed by combining two neuro-fuzzy blocks with a postprocessor.Each neuro-fuzzy block is a first order Sugeno type fuzzy inference system with 4-inputs and 1-output.Τhe proposed impulse noise detector consists of two modes of operation,namely, training and testing.As demonstrated by the experimental results,the proposed detector significantly outperforms other conventional detectors.

noise detection;neuro-fuzzy inference system;impulse noise

提出了一个包含两个自适应神经模糊推理系统和一个后处理块的网络，该网络可用于灰度图像脉冲噪声检测。网络中每个自适应神经模糊推理系统都是一个四输入单输出一阶Sugeno模糊推理系统。所提出的脉冲噪声检测方法分两步进行：对该网络进行优化训练，确定其参数；用优化后的网络对被椒盐脉冲噪声污染的图像进行噪声检测。实验结果表明，与其他传统检测方法相比，所提出的方法，更能有效检测出图像中椒盐脉冲噪声。

噪声检测；神经模糊推理系统；脉冲噪声

A

ΤP751

10.3778/j.issn.1002-8331.1303-0302

LUO Haichi,LI Yueyang,SUN Jun.Impulse noise detection method for images.Computer Engineering and Applications, 2013,49（15）：150-156.

国家自然科学基金（No.61170119）；中央高校基本科研业务费专项资金（No.JUSRP211A38）。

罗海驰（1973—），女，讲师，CCF会员，研究领域为人工智能和图像处理等；李岳阳（1973—），男，博士，副教授，CCF会员，研究领域为人工智能和图像处理等；孙俊（1971—），男，博士，副教授，研究领域为人工智能和智能控制等。E-mail：lyueyang@jiangnan.edu.cn

2013-03-20

2013-04-09

1002-8331（2013）15-0150-07

CNKI出版日期：2013-04-18 http://www.cnki.net/kcms/detail/11.2127.ΤP.20130418.1614.003.html