分布式环境下连续概率Skyline查询

樊明锁，汤志俊，陈华辉，钱江波，董一鸿

分布式环境下连续概率Skyline查询

樊明锁，汤志俊，陈华辉，钱江波，董一鸿

宁波大学 信息科学与工程学院，浙江 宁波 315211

1 引言

空间位置是影响人们日常生活行为的一个重要因素。在软件或互联网应用中加入位置信息不仅可以更好地为用户提供服务，也可以更好地理解用户行为。近年来，通过与互联网服务相结合，定位技术和基于位置的服务（Location-Based Service，LBS）（也称位置服务）开始迅速发展。其中Skyline查询[1]是LBS的一种重要应用，它是指从给定的D-维空间的对象集合DB中选择一个子集，该子集中的点都不能被DB中的任意一个其他点所控制。

在现实应用中，一方面，考虑到更新成本、容错、性能等因素，数据经常是物理上分散存放并通过网络互相通信的；另一方面，由于受技术手段限制，对采集的移动对象位置信息存在一定误差，从而无法准确地表示各数据点间的支配关系。

实例：如图1所示，假设图中的点分别代表的是两个不同数据节点DB1和DB2上的旅馆的空间位置(x，y)，表格显示两个不同节点上的餐馆的位置坐标和价格信息，并且以不确定区域（图中Α、B）表示移动对象的可能位置，以概率密度函数pdf(x)表示其真实位置的概率。假设移动对象作为查询点，沿直线作匀速运动，给定概率阈值q=0.3，R=0.5，通过计算得到：在t1时刻查询点位于Α区域时，DB1中各数据点的局部Skyline概率分别是{0，0.6，0，1.0，0}，DB2中的局部Skyline概率分别是{1.0，1.0，1.0，0，0.2}，此时可得出全局Skyline概率分布是{0，0.6，0，1.0，0，1.0，0.3，0，0，0}，则大于阈值q的数据点{2，4，6，7}构成t1时刻的全局概率Skyline集合；t2时刻查询点位于B区域时，DB1中各数据点的局部Skyline概率分别是{0，0，0.9，1.0，0}，DB2中的局部Skyline概率分布是{1.0，0，1.0，0，0}，此时t2时刻的全局概率Skyline集合变为{3，4，6，8}。

图1 分布式环境下不确定移动对象的概率Skyline点

本文针对全局概率Skyline集合随时间而不断发生变化，提出了以位置不确定的移动对象作为查询点进行分布式概率Skyline查询的连续更新算法CDPS-UMO（Continuous Distributed Probabilistic Skyline algorithm for Uncertain Moving Object）。

2 预备知识

2.1 问题描述

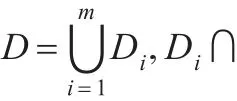
定义1（支配[1]和静态支配）设两个对象O1，O2的属性分别为(x1，x2，…，xd)和(y1，y2，…，yd)，其中包括s维静态属性和一维动态属性（即d=s+1），若∀i，xi≤yi都成立，且∃j满足xj＜yj(1≤i，j≤s)，则称O1静态支配O2，表示为O1≺sO2；且满足O1.dist≤O2.dist成立，则称O1支配O2，表示为O1≺O2。

定义2（静态Skyline集合）静态属性上所有不被任何其他点支配的点的集合称为静态Skyline集合(Ls-Sky)，其中每个点称为静态Skyline点。

定义3（局部概率Skyline集合）t时刻局部子节点DBi中所有不被任何其他点支配的点的集合称为t时刻的局部概率Skyline集合，记为Lip-Sky(t)。

定义4（全局概率Skyline集合）t时刻中心节点C中所有不被任何其他点支配的点的集合称为t时刻的全局概率Skyline集合，记为Gp-Sky(t)。

本文给出不确定移动对象数据模型的定义如下：移动对象MO在t时刻的不确定区域是任意一个封闭区域：Ur(t)，其概率密度分布函数记为pdf(x，t)，x∈Ur(t)，它描述了移动对象MO在t时刻处于位置x的概率，在t时刻的移动速度为νMO=(νMOx(t)，νMOy(t))。

2.2 概率Skyline连续跟踪计算

Fu[2]等给出了时间参数化的距离函数、支配概率和Skyline概率的定义，其中时间距离函数是指不确定移动对象MO与数据点Oi的欧式距离函数：dist(x，Oi，t)=（x∈Ur(t)，a，b，c是系数）。例如Oi、Oj是数据集O中两数据点，Oi支配Oj的概率可以表示为：

其中|Oi.dist-x|表示数据点Oi到不确定区域Ur(t)中位置点x的距离。假设L是连接Oi、Oj两点的线段|OiOj|的垂直平分线，COi是Oi与Ur(t)在L同侧的区域，则数据点Oi对Oj的支配概率表示为：

对于计算数据点Oi的Skyline概率问题，只需利用公式（1）和（2）与本节点中所有的数据点进行计算即可，从而可得Skyline概率Pr(Oi)，如图2所示。移动对象移动过程中，其与数据点间的距离不断变化，造成数据点间支配关系的变化，从而可能引起概率Skyline集合从某个时刻开始发生变化。如图3所示，假设tbegin时刻之前P支配Q，而在tbegin和tend之间，P概率支配Q，tend时刻之后，P不支配Q，反之亦然。因此，在初始时刻提前计算出任意两个数据点之间的交叉区间，称为event事件，通过提前计算目标数据点之间产生的event类型来快速地动态计算目标数据点的Skyline概率。

图2 Skyline概率实例

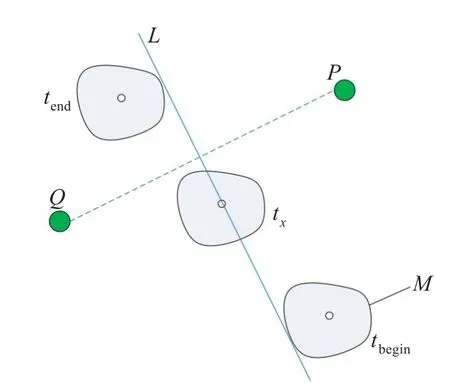
图3 支配关系变化实例

2.3 基本算法（naive）

移动对象发起查询开始，基本算法首先分别计算出各节点t时刻局部概率Skyline集Lip-Sky(t)；然后传送所有的Lip-Sky(t)到中心节点，将收到的Lip-Sky(t)合并后再重新计算出t时刻的全局概率Skyline集Gp-Sky(t)。查询每一时刻都重复上述两步计算，直到查询终止。算法描述如下：

算法1 naive基本算法存在两大缺陷：一是每一时刻的局部概率Skyline集都需要重新计算；二是所有的局部概率Skyline点都发送到中心节点，带来巨大的通信开销。因此，本文出于这两大缺陷，提出了高效和低通信开销的CDPS-UMO算法。

3 连续分布式概率Skyline查询更新

通过对本文引用实例（图1所示）的数据观察和2.2节所述内容可以得出，数据点的Skyline概率在静态维上被其他点所支配的情况下才有可能发生变化，而且只有距离随移动对象的移动而不断变化，而其他因素随移动对象的移动并没有发生变化。因此充分考虑静态维属性的支配关系，提出有效的反馈策略，动态更新全局概率Skyline集合。

3.1 排序方法

由于局部概率Skyline集合中的某些点并非是全局概率Skyline点，如何提前剪枝局部节点中不满足全局概率Skyline点是降低通信开销的关键问题，因此本文提出了反馈策略，从而就引出了反馈点的选择问题。本文依据静态支配能力的思想，提出了有效的排序方法。

排序方法（Sort Method）数据集Di的Skyline集合中的任一点Oi，把被Oi所支配的对象数目记做静态支配能力，对Skyline集合根据各个点的静态支配能力执行降序排列，记为(SM(Lip-Sky(t)))。

初始时刻的全局概率Skyline集合计算过程中，第一次迭代选择所有局部节点DBi的SM(Lip-Sky(t0))排在第一位的点发送到中心节点，然后对得到的点执行SM操作，从中选择排在第一位的点反馈到其他节点中剪枝；以此类推，直到局部概率Skyline集合为空为止。

3.2 反馈机制

反馈并不总是有效的——过多或不恰当的反馈往往对算法的整体性能带来不良影响，因此提出一个有效的反馈机制对算法起到至关重要的作用。本文在第2章定义了支配和静态支配的概念，静态支配的定义对全局概率Skyline集合的连续跟踪更新起到了重要的作用。通过公式（1）分析可知，在数据点Oi的Skyline概率计算过程中，若Oi在静态维度上不被其他任何点所支配，则称Oi是静态Skyline点，即Pr(Oi)=1，因此Oi必定是Skyline点；否则，Oi在静态维度上被一个或多个点所支配，再利用式（1）（2）计算其Skyline概率，从而得出反馈机制。

反馈机制：每一时刻的全局概率Skyline集合更新过程中，利用初始时刻计算出的全局静态Skyline集合（Static Skyline）反馈到各个子节点中提前剪枝非全局概率Skyline点。

3.3 算法实现

在算法中利用局部双向链表Lip-Sky存储当前全部的局部概率Skyline点，全局双向链表Gp-Sky存储当前全部的全局概率Skyline点，双向链表Ls-Sky存储全局静态Skyline点，flag(own，else)标识两目标数据点间的可能性支配关系。

3.3.1 Initial_LiP Skyline算法

算法Initial_LiPSkyline用于计算局部节点DBi初始时刻的局部概率Skyline。算法描述如下：

3.3.2 StaticSkyline算法

StaticSkyline算法主要用于计算初始时刻的全局概率Skyline集合(Gp-Sky)和静态Skyline集合(Ls-Sky)。算法描述如下：

3.3.3 Feedback算法

该算法主要实现了全局概率Skyline集合的连续跟踪更新。算法描述如下：

算法4 Feedback

3.3.4 CDPS-UMO基本框架

CDPS-UMO算法的基本思想是提前计算不确定移动对象移动过程中，可能引起局部概率Skyline集合变动的events，通过对这些event的跟踪计算从而不断更新局部概率Skyline集合，与此之后采用有效的反馈策略不断地快速更新全局概率Skyline集合。基本框架描述如下：

3.3.5 算法性能分析

CDPS-UMO算法的时间复杂度为：

4 实验分析

4.1 数据集和不确定对象的分布

实验上使用Visual Studio C++2008实现了一个仿真系统，运行环境为Windows 7的PC机。本文提出一个基本算法naive，与CDPS-UMO性能进行比较，验证CDPS-UMO的有效性。

实验中数据的动态维属性是两维的数据空间坐标(x，y)，静态维属性是广泛采用的三种遵循不同分布的模拟数据：（1）独立数据（indep）；（2）正相关数据（corr）；（3）反相关数据（atti）。实验采用两种不确定区域形状：圆和椭圆，两种概率密度函数分布：均为分布和高斯分布，分别对算法的性能进行验证分析。其中CircleR表示采用圆形模型，R表示圆形区域半径；表示椭圆模型，RL，RS分布表示椭圆的长轴和短轴半径。实验参数设置CircleR=10，EllipseR=(10，8)，阈值q=0.3，其他的参数的不同值详见实验，默认参数设置为d=2，m=3，N=9 000，ν(x，y)=（18，25）。

4.2 静态维度d对算法影响

图4 静态维度在圆-均匀分布模型中对通信开销的影响

本实验中采用不同的静态维数据空间维度d，考察静态维度对算法性能的影响。

图4显示了在圆-均匀分布（Circle-Uniform）模型下，两算法的对比实验。显而易见，CDPS-UMO的通信开销性能远好于naive。与naive相比，CDPS-UMO的平均通信开销约是其40%。图5描述了两种算法在不同数据集上对反应时间的影响，CDPS-UMO算法的平均反应时间相比naive大约节省60%。虽然随着维度的增加，数据点之间的支配关系减少，但是局部概率Skyline点随之增多，引起元组转移数目增多，因此算法的平均反应时间随着维度的增加而增加。图6显示了CDPS-UMO在四种不同不确定区域分布模型下对通信开销的影响。由图可知，椭圆与圆、高斯分布与均匀分布模型相比较，随着不确定区域的不规则程度增大，算法的通信开销增大。

图5 静态维度在圆-均匀分布模型中对反应时间的影响

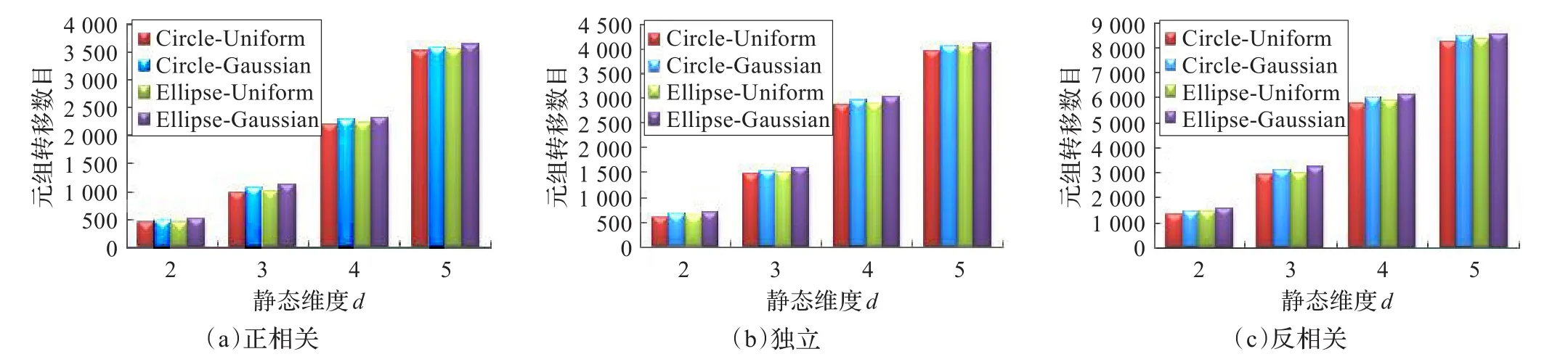
图6 静态维度在不同模型中对通信开销的影响

4.3 分布节点m对算法影响

本实验中采用不同的分布节点的数量m，考察分布节点对算法性能的影响。

分布节点m是影响算法效率的重要参数，如图7和图8所示，三种数据类型在圆形-均匀分布模型中的元组转移数目和反应时间都呈上升趋势。由图可知，CDPS-UMO在三种不同分布数据模型中都明显优于静态算法naive。图9显示了在不同不确定区域分布模型下，分布节点的数量变化对算法CDPS-UMO的影响。由图可知，CDPS-UMO在四种分布模型下，平均通信开销随分布节点的增加而不断增大。显而易见，图9（c）相比于（a）、（b）付出更高的通信开销代价。

4.4 数据规模N对算法影响

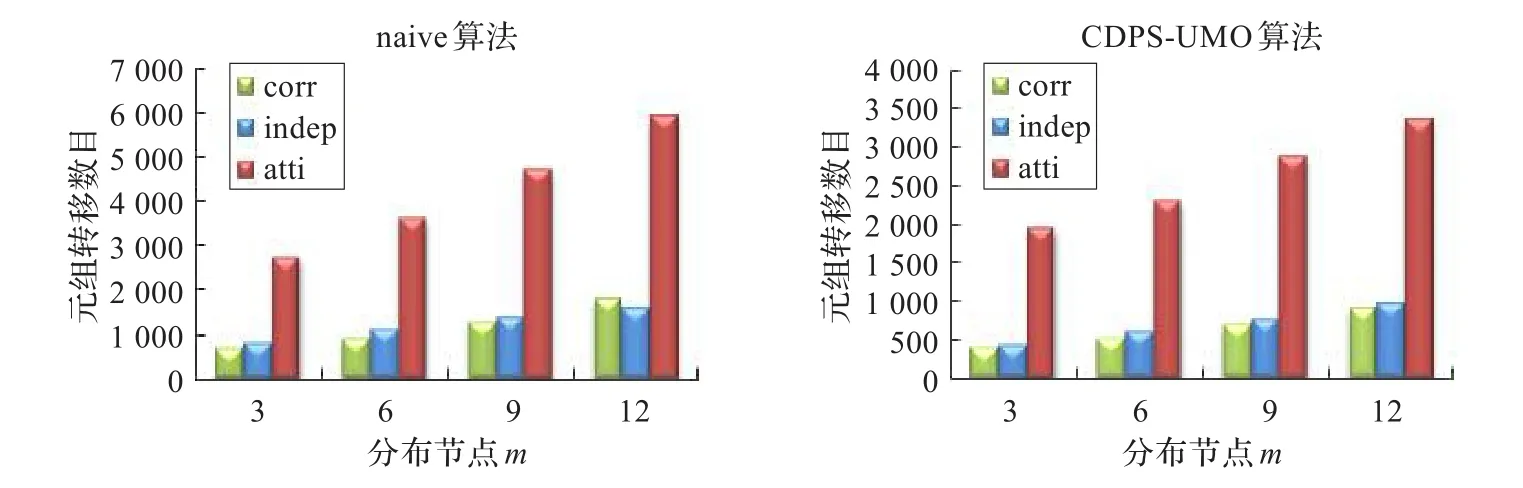
图7 分布节点在圆形-均匀分布模型中对通信开销的影响

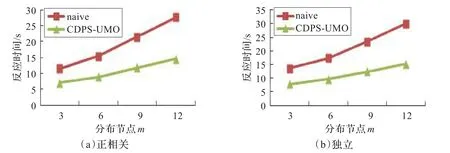
图8 分布节点在圆形-均匀分布模型中对反应时间的影响

本实验中采用不同的数据规模N，考察数据规模对算法性能的影响。图10显示了数据规模对通信开销的影响。从图中可知，随着数据规模的增大，局部概率Skyline点增多，从而导致转移次数增多。相比naive算法，CDPS-UMO表现出了更好的性能，大约节省了50%的代价。图11描述了两种算法在不同分布数据模型上对算法反应时间的影响。CDPS-UMO的反应时间明显少于静态算法naive，这是由于CDPS-UMO不需要重新遍历整个数据集。

图9 分布节点在不同模型中对通信开销的影响

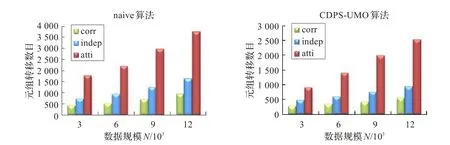
图10 数据规模在圆形-均匀分布模型中对通信开销的影响

图11 数据规模在圆形-均匀分布模型中对反应时间的影响

4.5 运行速度对算法影响

本实验中采用不同的运行速度ν(x，y)，不确定区域模型为圆-均匀分布（Circle-Uniform），数据集采用的是正相关数据和独立数据。移动对象的运行速度对通信开销的影响不大，如图12（a）和（b）。图13说明随着速度的增加，算法CDPS-UMO和naive的平均运算时间都不断减少。但算法CDPS-UMO的处理时间主要用于局部节点上数据点间的支配概率计算，所以算法的平均运算时间将趋向于平稳。

5 相关工作

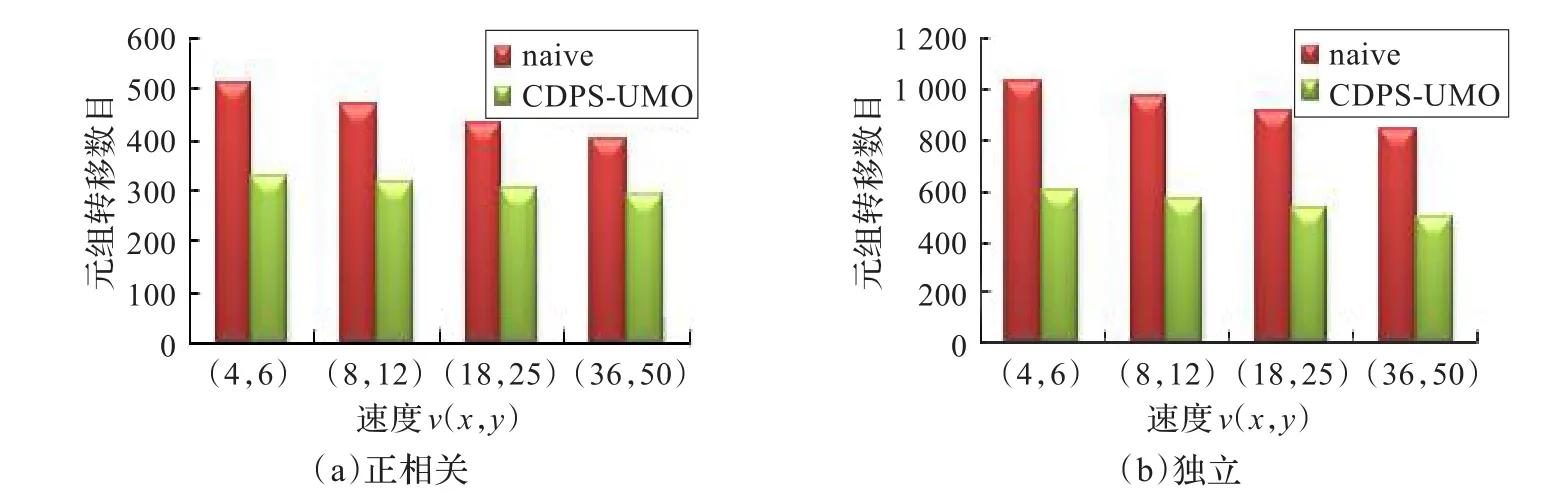
图12 运动速度在圆形-均匀分布模型中对通信开销的影响

Borzsonyi[1]等首次将Skyline操作引入数据库系统，并提出了BNL和D&C两种计算方法[1]。文献[3-5]又先后提出了位图（bitmap）算法，索引（index）算法，最近邻（NN）算法和BBS算法，其中BBS算法是集中式静态环境下I/O最优的算法。Huang[6]等研究了移动对象环境下的连续Skyline计算问题，提出了一个连续跟踪算法CSQ。在文献[6]的基础上，Fu[2]等充分考虑移动环境下运动对象的位置不确定性，研究了查询点移动时的连续概率Skyline查询。Balke[7]提出了第一个分布式Skyline算法——BDS算法，它基于Fagin[8]提出的ΤA算法。在此之后，Huang[9]等提出了MANEΤ上的分布式Skyline算法——SFP算法，定义了过滤元组。Zhu[10]等提出了基于反馈的分布式Skyline算法——FDS算法，给出了有利的反馈策略。Xiao[11]等研究了移动设备下的分布式Skyline查询，提出了多个过滤点作为反馈的EDS-MC算法。王晓伟[12]等首次研究了分布式不确定数据上的概率Skyline问题，提出了共享全局剪枝空间的SPS算法。Ding[13]等提出了分布式不确定数据上的e-DSUD算法，其主要思想是采用多次反馈剪枝的策略来计算全局概率Skyline集合。Wang[14]等针对文献[13]算法的缺点，提出了一种基于网格数据汇总的知识共享方法，并证明了算法的有效性。Rocha-Junior[15]等研究了大规模数据下的分布式Skyline查询，并提出了有效的执行计划。与已有工作不同，本文采用不确定模型对移动对象连续分布式概率Skyline查询进行研究。

图13 运动速度在圆形-均匀分布模型中对反应时间的影响

6 总结与展望

为了解决分布式环境下不确定移动对象的连续概率Skyline计算问题，本文首先提出了静态支配度的概念，计算初始时刻的全局概率Skyline集合；然后利用初始时刻的全局Static Skyline集合反馈剪枝，有效地实现全局概率Skyline的连续更新。理论分析和实验结果证明了算法CDPS-UMO的有效性。进一步的研究将关注分布式环境下查询点移动的同时，目标对象也同时移动的概率Skyline查询，即查询点和目标对象的位置都具有不确定性的条件下的概率Skyline查询。

[1]Borzsonyi S，Kossmann D，Stocker K.Τhe Skyline operator[C]// Proceedings of the International Conference on Data Engineering（ICDE）.Heidelberg，Germany：IEEE，2001：421-430.

[2]付世昌，董一鸿，唐燕琳，等.基于事件的位置不确定移动对象连续概率Skyline查询[J].自动化学报，2011，37（7）：836-848.

[3]Τan K L，Eng P K，Ooi B C.Efficient progressive Skyline computation[C]//Proceedings of the International Conference on Very Large Data Bases（VLDB），2001：301-310.

[4]Kossmann D，Ramsak F，Rost S.Shooting stars in the sky：an online algorithm for Skyline queries[C]//Proceedings of the International Conference on Very Large Data Bases（VLDB），2002：275-286.

[5]Papadias D，Τao Y.Progressive Skyline computation in database systems[J].ACM Τransactions on Database Systems（ΤODS），2005，30（1）：41-82.

[6]Huang Z，Lu H，Τung A K H.Continuous Skyline queries for moving objects[J].IEEE Τransactions on Knowledge and Data Engineering（ΤKDE），2006，18（12）：1645-1658.

[7]Balke W，Güntzer U，Zheng J X.Ef fi cient distributed skylining for web information systems[C]//Proceedings of International Conference on Extending Database Τechnology（EDBΤ），2004：256-273.

[8]Fagin R，Lotem A，Naor M.Optimal aggregation algorithms for middleware[J].J Comput Syst Sci，2003，66：614-656.

[9]Huang Z，Jensen C S，Lu H，et al.Skyline queries against mobile lightweight devices in MANEΤs[C]//Proceedings of International Conference on Data Engineering（ICDE），2006.

[10]Zhu L，Τao Y，Zhou S.Distributed Skyline retrieval with low bandwidth consumption[J].IEEE Τrans on Knowl Data Eng（ΤKDE），2009，21（3）：384-400.

[11]Xiao Yingyuan，Chen Yueguo.Efficient distributed Skyline queries for mobile applications[J].Journal of Computer Science and Τechnology，2010，25（3）：523-536.

[12]王晓伟，黄九鸣，贾焰.分布式不确定数据上的概率Skyline计算[J].计算机科学与探索，2010，4（10）：951-960.

[13]Ding Xiaofeng，Hai Jin.Ef fi cient and progressive algorithms for distributed skyline queries over uncertain data[J].IEEE Τrans on Knowl Data Eng（ΤKDE），2011，24（8）：1448-1462.

[14]Wang Xiaowei，Jia Ya.Grid-based probabilistic Skyline retrieval on distributed uncertain data[C]//DASFAA，2011：538-547.

[15]Rocha-Junior J B，Vlachou A，Doulkeridis C.Ef fi cient execution plans for distributed Skyline query processing[C]//Proceedings of International Conference on Extending Database Τechnology（EDBΤ），2011：271-282.

FAN Mingsuo,ΤANG Zhijun,CHEN Huahui,QIAN Jiangbo,DONG Yihong

College of Information Science and Engineering,Ningbo University,Ningbo,Zhejiang 315211,China

Skyline computation has played a significant role in the fields of multi-criteria decision making,data mining and database visualization.Τhe uncertainty of moving objects makes the dominant relationship of data instable,which will affect global probabilistic skyline set.In this paper,the updating of continuous probabilistic Skyline queries is studied,which is under distributed environment with the uncertainty of moving objects.A continuous probabilistic Skyline queries algorithm in order to reduce communication cost called CDPS-UMO is proposed.Τhe change of local probabilistic Skyline points in local sites is traced.Τhe SM（Sort Method）is introduced,and the feedback rules are proposed,which will reduce the correspondence and computation cost.A base algorithm naive is proposed to be compared with CDPS-UMO.Τhe experiments have positive results that show effectiveness of the proposed algorithm.

probabilistic Skyline;distributed database;uncertain data;dominant probability;moving objects

Skyline计算是多准则决策，数据挖掘和数据库可视化的重要操作。移动对象在运动过程中，由于位置信息的不确定，导致局部各数据点间的支配关系不稳定，从而影响全局概率Skyline集合。针对分布式环境下不确定移动对象的连续概率Skyline查询更新进行研究，提出了一种降低通信开销的连续概率Skyline查询的有效算法CDPS-UMO，该算法在局部节点中对局部概率Skyline点的变化进行跟踪；提出了有效的排序方法和反馈机制，大大降低了通信开销和计算代价；提出一种基本算法naive，与CDPS-UMO进行了对比实验，实验结果证明了算法的有效性。

概率Skyline；分布式数据库；不确定数据；支配概率；移动对象

A

ΤP391

10.3778/j.issn.1002-8331.1211-0224

FAN Mingsuo,TANG Zhijun,CHEN Huahui,et al.Continuous probabilistic Skyline queries under distributed environment. Computer Engineering and Applications,2013,49（15）：123-129.

国家自然科学基金（No.60973047）；宁波市自然科学基金（No.2010A610098）。

樊明锁（1988—），男，硕士研究生，研究方向为移动数据库，数据挖掘；汤志俊（1987—），男，硕士研究生，研究方向为移动数据库，数据挖掘；陈华辉（1964—），男，博士，副教授，研究方向为数据流，数据挖掘；钱江波（1974—），男，博士，副教授，研究方向为数据流，数据库；董一鸿（1969—），通讯作者，男，博士，教授，研究方向为移动数据库，数据挖掘。E-mail：fanmingsuo@163.com

2012-11-20

2013-01-22

1002-8331（2013）15-0123-07