混沌理论和LSSVM相结合的网络流量预测

张文金，许爱军

广州铁路职业技术学院 教育技术中心，广州 510430

混沌理论和LSSVM相结合的网络流量预测

张文金，许爱军

广州铁路职业技术学院 教育技术中心，广州 510430

网络流量是衡量网络运行负荷和状态的重要参数，通过对网络流量进行监测，可以及时了解网络系统运行状况，因此网络流量预测成为当前一个重要研究课题[1]。

目前网络流量预测方法主要有两类：一类是以时间序列法为代表的传统预测方法[2]；另一类是以神经网络为代表的人工智能预测方法[3]。传统时间序列模型只能处理短相关网络流，然而随着网络测量技术的发展，网络研究人员发现高速网络的业务具有长相关性（相似性），这是传统方法不能处理的，因此时间序列预测方法应用受限[4]。神经网络采用经验风险最小化准则，要求训练样本大，易产生过拟合（即泛化能力不强），导致预测精度下降，且神经网络的结构复杂，隐含层节点数等难以恰当选择，随着输入维数的增加，神经元个数急剧增加往往导致“维数灾”难题，这些都大大限制了神经网络应用[5]。支持向量机（Support Vector Machine，SVM）是一种基于结构风险最小化原则的人工智能学习算法，较好地解决了小样本、非线性、高维数和局部极小点等实际问题，广泛应用于网络流量的预测领域[6-7]。但SVM预测性能不仅与自身参数相关，还与网络流量的训练样本相关，当前主要采用人为确定训练样本的输入和输出矩阵，采用均方根误差对模型的逼近能力和预测效果进行评价，该方法的不足之处是训练样本选取缺乏理论指导，一旦选定就只能通过预测值与真实值之间的误差来反复修正模型，直到模型达到满意的预测精度，导致训练时间长，容易产生过拟合现象[8]。大量的实验证明，网络流量存在非平稳性、时变性、混沌性等特性，需要采用非线性混沌理论对网络流量预测进行建模[9]。

在混沌理论的相空间重构基础上，本文将最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）作为预测模型拟合网络流量相空间中相点的演化趋势，建立一种基于混沌理论和LSSVM相结合的网络流量预测模型。首先通过混沌理论的相空间重构将一维的网络流量时间序列转化成矩阵形式，然后通过LSSVM对构造时间序列进行训练，从而避免了LSSVM在训练过程的数据选取的盲目性，最后采用具体网络流量数据进行仿真实验，仿真结果表明该方法能明显提高网络流量的预测精度，获得了满意的预测效果。

1 相空间重构和最小二乘支持向量机

1.1 基于混沌理论相空间重构

相空间重构（Phase Space Reconstruction，PSR）基本思想为：系统中任一分量的演化均由与之相互作用着的其他分量所决定，因此在进行相空间重构时，只需考察一个分量，并将它在某些固定的时间延迟点上的测量作为新维处理，它们确定了某个多维状态空间中的一点，不断重复这一过程并测量相对于不同时间的各延迟量，就可以产生出许多这样的点，将吸引子的许多性质保存下来，就可以通过采用系统的一个分量重构出原动力系统模型，初步确定系统的真实相空间的维数[9-10]。

假设观测到的混沌时间序列为：{x(t)};t=1，2，…，n，其中n表示样本个数，根据Τakens定理，通过选定合适的延迟时间（τ）和嵌入维（m）就可以将混沌时间序列时间重构为：

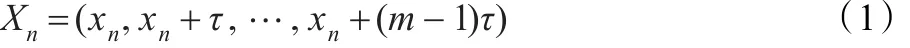
从式（1）可知，相空间重构结果的好坏由m和τ决定。实验研究表明[11-12]，如果τ选取不适合，导致信息冗余或丢失，而m太小，不足以展示复杂行为的细致结构；太大却会使计算工作大大复杂化，所以τ与m的正确选取对混沌时间序列分析有着重要的意义。

当前，针对τ和m的选取有两种思想，一种是两者分开、独立选择，别一种应该联合选择。根据Τakens定理，对于无限长的、无噪声的时间序列，τ可以任意选择，即与m无关，但实际时间序列不可避免地带有噪音且不能保证序列长度足够，因此，现在多数研究者认为τ和m是相互关联的，应该同时进行[11]。由于C-C方法在确定时间延迟过程中同时得到合适的嵌入维数，且该方法操作容易、计算量小、对小数据组可靠且具有较强的抗噪声能力，因此本文采用C-C进行相空间重构，具体计算过程见文献[12]。

1.2 最小二乘支持向量机

Suykens等在标准支持向量机的基础上提出了最小二乘支持向量机（LSSVM），其将标准支持向量机型中的损失函数设定成误差平方和，把不等式约束改成等式约束，减少待定参数，又将求解二次规划的问题转化成线性KKΤ（Karush Kuhn Kucker）方程组的求解，降低了求解的复杂性[13-14]。

对于样本集{(xi， }yi)，i=1，2，…，n，xi和yi分别表示样本输入和输出，通过非线性映射函数φ(·)将样本映射到高维特征空间，从而获得最优线性回归函数：

式中，w为特征空间的权值向量，b为偏置量。

根据结构风险最小化原则，式（2）问题求解的LSSVM回归模型为：

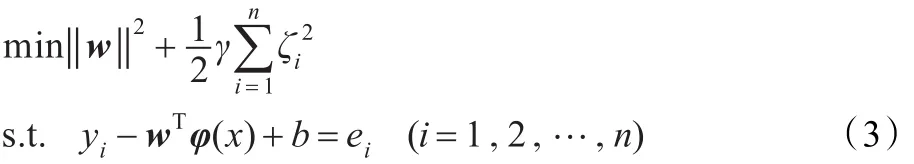
式中，γ为惩罚参数，平衡训练误差和模型复杂度；ei为实际值与预测值间的误差。

通过引入拉格朗日乘子将上述约束优化问题转变为无约束对偶空间优化问题，即

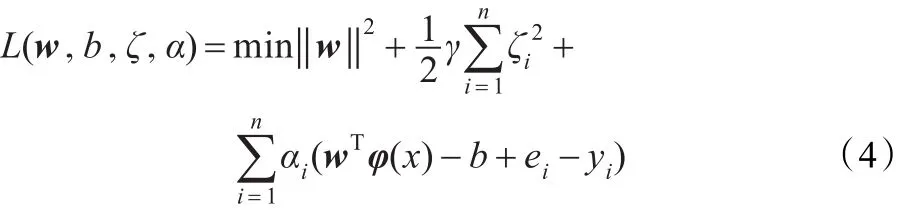
式中，αi为拉格朗日乘子，γ表示核函数参数。

对于非线性预测问题，通过引入核函数进行求解，根据Mercer条件，核函数定义如下：

本文选择径向基核函数作为LSSVM核函数，径向基核函数定义为：

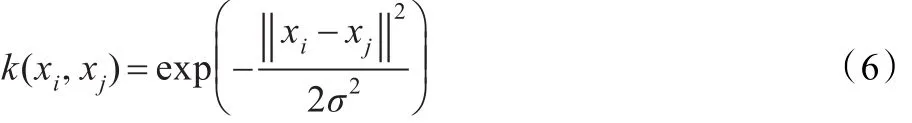
最后LSSVM回归模型为：

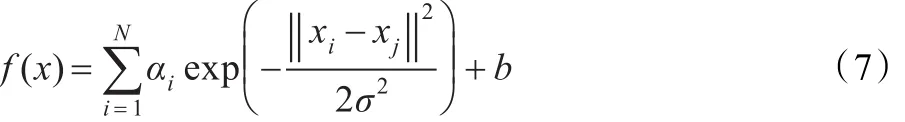
式中，σ表示径向基核数宽度。

从上述LSSVM建模过程可知，基于径向基核函数的LSSVM预测性能主要取决于γ和σ，当前参数选择方法主要有梯度下降算法、网络搜索算法、粒子群优化算法和遗传算法等，梯度下降算法对初始值敏感，网络搜索算法，计算量大，搜索速度慢；遗传算法和粒子群算法，极易陷入局部最优，为此本文采用混沌粒子群算法对LSSVM的参数γ和σ进行优化，具体优化过程如图1所示。

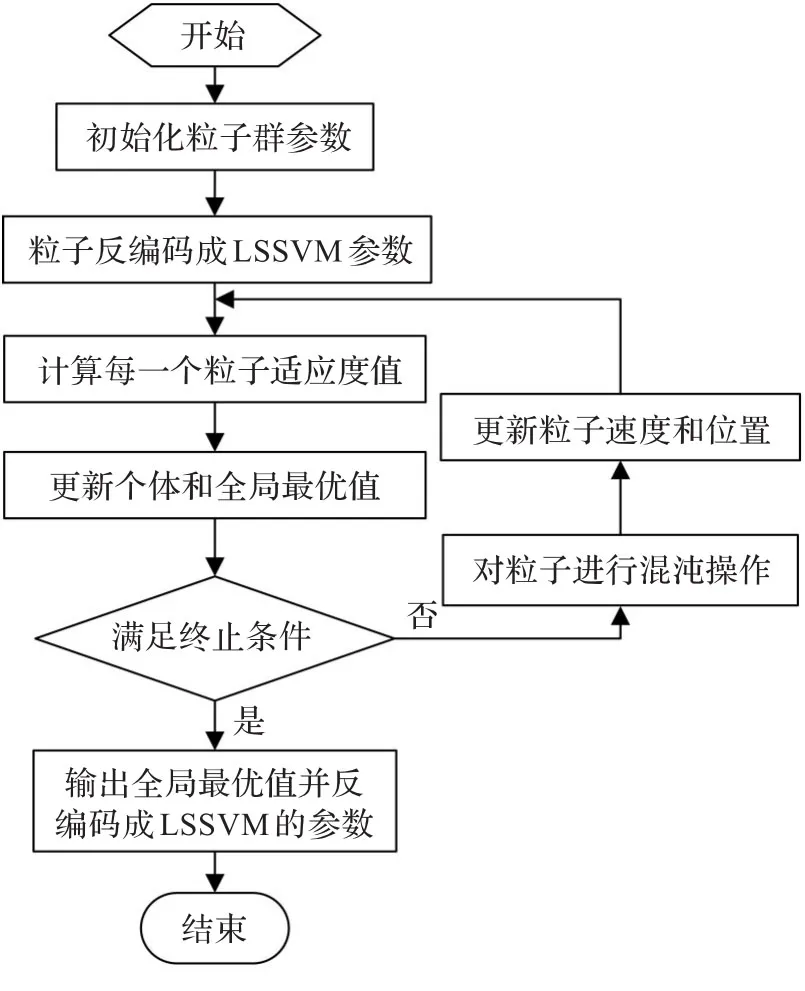
图1 基于混沌粒子群的LSSVM参数优化流程

2 混沌理论和LSSVM结合的网络流量预测模型

2.1 训练预测前的数据预处理

网络流量受到多种因素影响，具有非线性和随机性，数据之间相差比较大，LSSVM对0到1之间数据最为敏感，为此，将数据输入到LSSVM进行训练之前，对网络流量数据进行归一化处理，具体为：

最后对网络流量预测结果进行反归一化处理，恢复真实预测值。

式中，x表示网络流量原始数据，xmax和xmin表示网络流量最大值和最小值。

2.2 预测模型输入输出结构

混沌相空间中任一相点xi演变到下一相点xi+1可以用函数关系表示为：

由于xi+1的前m-1个分量都是已知的历史数据，为简单起见只要构造一个映射F作为预测器，使得︵=f(xi)即可。但是，由于F是吸引域内的未知映射且系统具有强非线性，因此只能从观测数据得到系统动力学行为，因此采用LSSVM拟合非线性映射函数F，其输入节点的数目取相空间的饱和嵌入维数m，输出节点为1个。

2.3 训练样本集构成方法

为减少不相关相点对预测的不良影响，本文的训练样本集按预测相点的最近邻点集原理生成，它能增强预测模型对系统混沌动力学的联想和泛化推理能力[15]。实验中使用预测中心点的k个近邻作为样本进行模型训练，其中近邻相点的求取按照欧氏距离标准，即

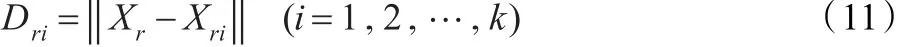
式中，Xr表示预测中心相点；Xri表示Xr的第i个近邻相点。

“都过去了，不会计较你的。若找不到工作，回来跟我干，不会亏待你。”“包子西施”没有作声，像见不得人似的，捂着脸跑了。

2.4 预测步骤

基于混沌理论和LSSVM相结合的网络流量具体预测步骤如下：

（1）根据上述的方法对网络流量原始数据进行预处理。

（2）相空间重构。采用C-C方法选取最佳延迟时间和嵌入维数，继而建立网络流量时间序列的多维相空间。

（3）按照上述的方法构造模型的输入、输出变量，并采用K近邻算法选择样本，形成训练样本集。

（4）模型训练。采用混沌粒子群算法对LSSVM模型参数进行优化，在样本数据集上进行训练。

（5）预测。将预测中心点数据代入上一步训练得到的模型中，即可获得对未来网络流量的预测值。

3 仿真实验

3.1 数据来源

实验数据来源于网络流量文库：http：//newsfeed.ntcu. net/～news/2011/，收集了主节点路由器Incoming articles从2011年8月1日到2012年2月20日的每小时网络访问流量，得到4 400个数据，这些数据组成了一个一维网络流量时间序列{x(t)，t=1，2，…，4 400}，为了全面测试本文网络流量预测模型的有效性，并对不同训练样本和测试样本比较对模型预测性能的影响，将训练样本数∶测试样本数=100∶1；50∶1；20∶1；10∶1；5∶1；2∶1，训练样本集通过相空间重构和LSSVM建立网络流量预测模型；测试样本集对建立的网络流量预测模型的泛化推广能力进行预测检验，网络流量时间序列数据如图2所示。

图2 网络流量原始数据

在网络流量的预测研究中，预测算法和样本集选择方法均影响预测精度，为检验本文提出的网络流量预测方法的有效性，构造了5个预测模型进行比较。

（1）模型1：采用加权一阶局域法（Adding Weight One rank Local region method，AWOL）对网络流量混沌时间序列进行预测。

（2）模型2：采用混沌理论与BP神经网络相结合的预测方法（PHR-BPNN），首先采用混沌理论的相空间重构对网络流量进行重构，然后使用BP神经网络对相点演变规律进行建模，从而得到网络流量预测结果，但该模型仅直接选择预测中心点的前k个相点作为训练样本。

（3）模型3：采用LSSVM作为预测模型，其他与模型2相同。

（4）模型4：采用BP神经网络作为预测模型，但此时训练样本集由预测中心相点的k个最近邻构成，其他与模型2一致。

（5）模型5：与模型3一样，也是采用LSSVM作为预测器，但样本选择与模型3不同，而是采取与模型4一样的方法，各模型的预测方法及样本选择见表1。

表1 五种模型的预测方法和样本选择

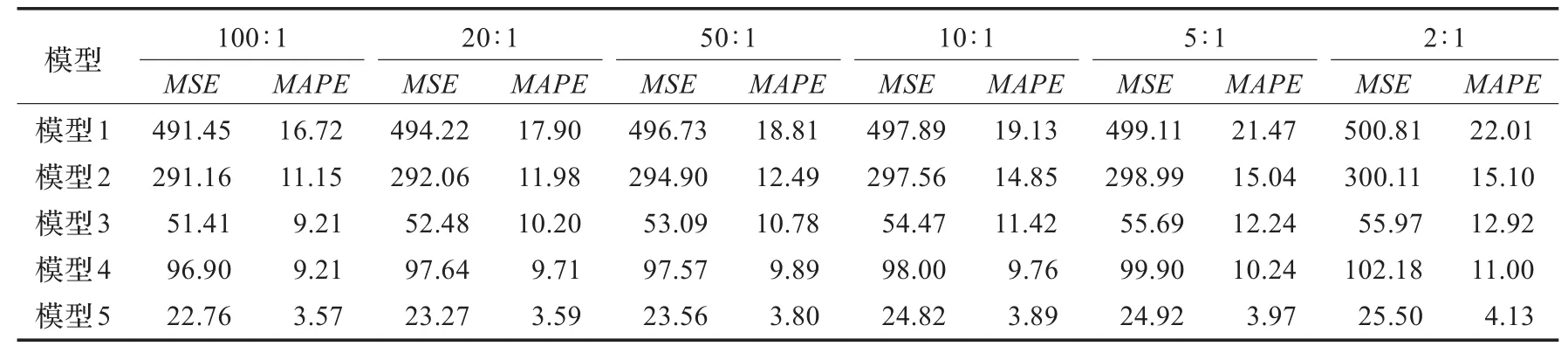
表2 五种模型对不同训练样本数和测试样本数的预测误差结果比较

为了评价模型性能，采用均方误差（Mean Squared Error，MSE）和平均相对百分比误差（Mean Absolute Percent Error，MPAE）作为模型性能评价指标，它们定义如下：

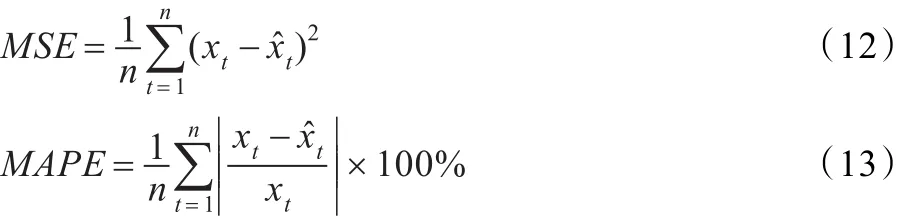
式中，xt表示网络流量实际观测值，xˆt表示预测值，n表示所预测的网络流量样本数。

3.3 模型的实现

首先对网络流量历史数据进行归一化处理，然后采用C-C方法确定最优延迟时间τ=1和嵌入维m=5，然后采用最近邻法选择训练样本集，最后采用LSSVM进行训练建模，并采用粒子群算法优化LSSVM的参数，最后对测试集进一步预测，得到的结果如表2所示。

3.4 结果分析

（1）从表2的对比结果可知，主要是因为加权一阶局域法采用线性方法拟合混沌的网络流量时间序列相点的演化规律，虽然计算简单，运行速度快，但网络流量时间序列本质上是非线性、时变性的，其相空间发展规律不能只使用线性方法进行拟合，而其他模型采用的是非线性方法，符合相空间的本质特征，因此预测效果更好，但是加权一阶局域法的预测速度要快于其他非线性预测模型，时间复杂度最低。

（2）模型3比模型2，模型5比模型4的效果要好，主要是因为模型2和模型4使用BP神经网络进行建模，而BP神经网络是基于经验风险最小化原则的非线性学习算法，容易出现过拟合，降低了预测模型的泛化能力，因此预测精度较低，预测误差比较大，预测性能较差，而模型3和模型5使用LSSVM进行建模，LSSVM采用结构风险最小化原则，可以取得更好的推广能力以提高预测精度。基于LSSVM的模型训练速度要明显慢于基于BP神经网络的速度，训练时间和空间复杂度较高，然而模型一旦建立，预测速度和BP神经网络差不多，即预测时间和空间复杂度没有什么大的区别。

（3）模型4比模型2，模型5比模型3的预测精度更高，主要是因为模型4和模型5采用最近邻样本训练集，避免了不相关点的不良影响，因此取得了更好的预测效果，尤其是模型5预测性能最好，大幅提高了网络流量的预测精度。对比结果表明，本文提出的混沌理论和最小二乘支持向量机结合的网络流量预测模型是有效、可行的，为具有混沌特性的网络流量时间序列预测问题提供了一种新的解决思路。

（4）从表2可知，当训练样本和测试样本数不同时，其预测结果差异很大，当训练样本越大时，预测精度越高，预测误差相对较小，说明训练样本数目越大，提供最优K邻点信息就越丰富，更加能够准确描述网络流量变化趋势，预测结果更加可靠，泛化推广能力越强。

4 结论

针对网络流量非线性、混沌等特点，提出了基于混沌理论和LSSVM相结合的网络流量预测方法，并采用实际网络流量数据进行了仿真测试。测试结果研究表明：

（1）针对网络流量非线性、非平稳的特点，通过引入混沌理论，对网络流量时间序列进行相空间重构，将其整理为5维状态空间向量序列，最大可能地提取和恢复网络流量的演化信息。

（2）LSSVM采用结构风险最小化原则，解决了在神经网络方法中易陷入局部最小值、精度与泛化不可调和的矛盾，可以减少过拟合风险，使用该方法进行预测比BP神经网络和加权一阶局域法有更好的效果。

（3）采用预测相点的最近邻点构成模型训练样本集可以有效提高预测精度。

（4）基于混沌理论和LSSVM的网络流量预测方法可以大幅提高网络流量预测精度，具有广泛应用前景。

[1]程光，龚俭.大规模网络流量宏观行为周期性分析研究[J].小型微型计算机系统，2003，24（6）：992-994.

[2]高波，张钦宇，梁永生.基于EMD及ARMA的自相似网络流量预测[J].通信学报，2011（4）.

[3]曹建华，刘渊，戴悦.一种基于灰色神经网络的网络流量预测模型[J].计算机工程与应用，2008，44（5）：155-157.

[4]Jin Yi，Zhou Gan.Τheoretical mean-variance relationship of IP network traffic based on ON/OFF model[J].Sci China Ser F-Inf Sci，2009，52（4）：645-655.

[5]饶云华，曹阳，杨艳.自相似网络通信量的多尺度预测研究[J].计算机工程与应用，2005，41（28）：26-28.

[6]王俊松，高志伟.基于RBF神经网络的网络流量建模及预测[J].计算机工程与应用，2008，44（13）：6-7.

[7]Chen Z，Delis A，Wei P.A pragmatic methodology for testing intrusion prevention systems[J].Computer Journal，2009，52：429-460.

[8]孙知信，张玉峰.基于多维支持向量机的P2P网络流量识别模型[J].吉林大学学报：工学版，2010，40（5）：1298-1303.

[9]孙韩林，金跃辉，崔毅东，等.粗粒度网络流量的灰色模型预测[J].北京邮电大学学报，2010，33（1）：7-11.

[10]谢高岗，闵应骅，张大方，等.一个基于实际测试的网络流量模型[J].计算机工程与科学，2001，23（5）：51-54.

[11]Icol D M，Yan G.High-performance simulation of low-resolution network flows[J].Simulation，2006，82：21-42.

[12]Kim H S，Eykholt R，Salas J D.Nonlinear dynamics，delaytimes，and embedding windows[J].Physica D，1999，127：48-60.

[13]Zhong Weimin，Pi Daoying，Sun Youxian.Support vector machine based nonlinear model multi-step-ahead optimizing predictive control[J].Journal of Central South University of Τechnology，2005，12（5）：591-595.

[14]Pan Jinshui，Hong Meizhu，Zhou Qifeng，et al.Integrated application of uniform design and least-squares support vector machines to transfection optimization[J].BMC Biotechnology，2009，9（1）：52-57.

[15]孙雅明，张智晟.相空间重构和混沌神经网络融合的短期负荷预测研究[J].中国电机工程学报，2004，24（1）：44-48.

ZHANG Wenjin,XU Aijun

Education Τechnology Center,Guangzhou Institute of Railway Τechnology,Guangzhou 510430,China

In order to improve the prediction accuracy of network traffic,this paper proposes a network traffic forecasting method based on chaotic theory and Least Squares Support Vector Machine.Phase space reconstruction is used to reconstruct the network traffic time series and restore the network flow evolution path,and then the network traffic time series are modeled and trained by Least Squares Support Vector Machines which has good nonlinear forecasting ability,and the parameters of Least Squares Support Vector Machine are optimized by chaotic particle swarm algorithm to obtain the optimal network traffic forecasting model.Τhe forecasting method is tested by the network traffic time series data.Τhe results show that the method can well depict the network flow change trend and improves the forecasting accuracy of network traffic whose forecasting performance is superior to the traditional forecasting method.

chaotic theory;Least Squares Support Vector Machine（LSSVM）;network traffic;forecasting model

为提高网络流量的预测精度，提出一种基于混沌理论和最小二乘支持向量机相结合的网络流量预测方法。采用相空间重构对网络流量时间序列进行重构，恢复网络流量的演化轨迹，采用非线性预测能力强的最小二乘支持向量机对网络流量时间序列进行训练建模，采用混沌粒子群算法对最小二乘支持向量机参数进行优化，从而获得最优网络流量预测模型。用实际网络流量数据对该算法有效性进行验证，结果表明该方法能够很好刻画网络流量的变化趋势，提高了网络流量的预测精度，预测性能优于传统的预测方法。

混沌理论；最小二乘支持向量机；网络流量；预测模型

A

ΤP181

10.3778/j.issn.1002-8331.1201-0014

ZHANG Wenjin,XU Aijun.Network traffic forecasting based on chaotic theory and Least Squares Support Vector Machine.Computer Engineering and Applications,2013,49（15）：101-104.

张文金（1972—），讲师/工程师，研究方向：计算机网络、智能计算；许爱军（1978—），男，副教授，研究方向：计算机网络应用、数据挖掘。E-mail：zhangwenjin_2009@126.com

2012-01-04

2012-03-13

1002-8331（2013）15-0101-04

CNKI出版日期：2012-06-18 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120618.1131.001.html