基于椭圆曲线零知识的RFID双向身份认证

王笑梅，张秋剑

上海师范大学 信息与机电工程学院，上海 200234

基于椭圆曲线零知识的RFID双向身份认证

王笑梅，张秋剑

上海师范大学 信息与机电工程学院，上海 200234

针对RFID系统中标签与读写器的攻击，从攻击方式来看，主要有两种形式：一是直接攻击，利用电子通信对RFID系统的不同物理位置实施攻击。如拒绝服务攻击（DoS），攻击者可以通过一些射频信号装置短时间内向读写器端发送大量数据信号，导致RFID系统被大量的信号所淹没，使系统丧失处理正常数据的能力，陷入停滞状态[1]。另一种是身份欺骗攻击，电子标签是存储一定数据的信息源，与社会工程学相关的安全威胁会被黑客或者攻击者利用，成为新型的信息化犯罪。从攻击实施的位置上看，可以通过造标签，欺骗读写器，从而将非法数据信息送入系统；也可以通过伪造读写器，在用户不被觉察的情况下读取用户的标签信息，窃取用户隐私；还可以通过射频设备在空中截获标签与读写器之间的通信，从而利用这些设备伪造读写器或者电子标签，展开数据攻击、病毒攻击、ONS攻击等多种具体的入侵方法。本文设计的认证方案主要用于对抗第二种形式的攻击，即身份欺骗攻击，其主要形式有[1]：

（1）嗅探：攻击者可以窃听标签与读写器之间的通信，获取其中有用的信息和数据。这种窃取信息的行为可能不被RFID系统和用户所觉察。

（2）标签追踪：电子标签中常存储机要的或者个人隐私的信息，攻击者可以利用RFID便携设备，在用户不知情的条件下，查询用户的电子标签，从而非法获取用户数据，并可与个人身份或携带标签的物体位置相关联。

（3）重播攻击：攻击者可以使用RFID中继设备截获RFID信号，将其中的数据保存下来，并不断重复地发送给读写器。由于这些数据是真实有效的，所以系统就会以正常接收的方式处理这些数据。

（4）篡改信息：攻击者通过获取到的标签数据，利用空白或可擦写的标签制造“真实的”RFID标签，将一些非法信息写入标签内；或者直接修改某个非法获得的标签上信息，然后用篡改后的标签访问读写器，从而攻击RFID系统。

1 相关协议分析

RFID系统中，电子标签具有一定的数据存储和处理能力，可以进行数据加密、数字签名、身份认证等应用。其自身存在存储容量和计算速度限制的特点，且被动标签电源供给有限。随着RFID系统应用越来越广泛，很多电子标签中存储信息的敏感度以及安全性要求较高，所以，在设计安全协议时要做到低成本、低功耗、轻量级，在选择加密体制时应根据上述特点选择较为适合的加密算法。

随着RFID技术的发展，国内外学者已提出了许多安全协议，包括基于对称加密体制的认证协议[2-6]。主要有哈希函数或AES算法的协议，例如文献[2]提出的基于哈希函数的认证协议，在每次通信时阅读器都生成一个随机数r，与标签ID的更新相结合，可以防止重放攻击和位置检测，但一个会话如果被非法终止，容易导致标签的位置检测攻击与ID更新非同步攻击，且不能有效防止假冒攻击。这些基于对称加密体制的协议较简单，能满足RFID标签有限存储空间和计算能力的特性，以确保RFID标签的低成本，但现在很多RFID应用需要能确保更高的安全等级。近年来，RFID的运算能力越来越强，公钥计算的复杂性已不再成为瓶颈。基于公钥密码体制的安全协议在RFID技术的研究和应用中越来越广泛。然而一些知名的公钥加密算法密钥长度太大，运算代价太高，因而部分研究者将注意力转向椭圆曲线加密技术（Elliptic Curves Cryptosystems，ECC）。

ECC是利用有限域上的椭圆曲线有限群代替基于离散对数问题密码体制中的有限循环群后得到的一类密码体制。与其他公钥算法相比，ECC有非常大的优越性[7]：抗攻击性强，相同的密钥长度，其抗攻击性要强很多倍；存储空间占用小，其密钥长度和系统参数比RSA、DSA要小得多；带宽要求低，尤其应用于短消息加解密时；计算量小，处理速度快，总的速度比RSA要快得多，如在一定的相同计算资源条件下，160 bit的ECC算法的签名时间为3.0 ms，密钥对生成时间为3.8 ms，而1 024 bit的RSA算法却分别高达228.4 ms和4 708.3 ms，且随着密钥长度的增加，ECC存储空间较小的优势会愈加明显。因此，ECC特别适用于在计算能力和存储空间上都有局限性的RFID系统。

基于ECC的认证协议主要有文献[8-12]。文献[8]中介绍了基于有限域GF(2n)上的椭圆曲线的硬件实现，为了达到面积小和速度快的目标，设计中采用Montgomery阶梯算法来进行椭圆曲线上点的计算，以节省存储空间；同时由于采用了射影坐标，使得整个过程只需要在读写器上进行一次模逆计算，从而大大提高了速度，但其不具有向前安全性。文献[9]利用修正的椭圆曲线数字签名算法实现读写器和标签之间的签名和验证，提供一个双向身份验证协议。文献[10]提出的是基于ECC的ASPECΤ协议，该协议具有一定高效性，但也不具备向前安全性。文献[11]提出的是基于ECC的ASK协议，该协议存在已知密钥攻击缺陷，甚至不能完成相互认证，用户身份的保密性也存在问题。文献[12]介绍了一个近似椭圆曲线运算器，并提出了基于Okamoto的标签认证协议并进行性能分析。

本文在椭圆曲线加密体制的基础上，引入零知识身份证明思想，提出了一种基于椭圆曲线零知识的双向认证协议，具有更高的安全性和效率，能够较好地防御各种身份欺骗攻击，保障通信的安全与隐秘。

2 基本原理

2.1 椭圆曲线加密体制的基本原理

椭圆曲线密码体制是在各种涉及有限域乘法群的公钥密码体制中，用有限域上的椭圆曲线构成的群来类比有限域上的乘法群，从而获得类似的公钥密码体制。这类体制的安全性是基于椭圆曲线离散对数问题（ECDLP）求解的困难性。从而引出椭圆曲线密码技术的核心，由有限域上椭圆曲线的点所构成的Abel群的离散对数问题。

2.2 零知识协议的基本原理

零知识证明是指证明者（prover）在不泄露任何信息的情况下向验证者（verifier）证明自己知道秘密。假设证明者P拥有秘密S，并需要向验证者V证明。V首先向P发送若干问题中的一个，问题只能够P回答，而且问题只是与S相关，在一定程度上并不泄露任何关于S的信息；P收到后，向V发送这个问题的答案；然后V继续选取问题向P发送；以上过程重复n次，全部成功即可证明P拥有S。在这个过程中，为了做到不泄露任何与秘密相关的信息，V与P之间安全连续的信息交换主要依靠选取随机数值[13]。

在V与P通过通信信道连续的信息交换过程中，如果攻击者采用偷听的方式，那么他一次获得的信息只可能是某一次的问题，或者答案。因为认证过程是随机的，所以获得的信息不能帮助他来完成对RFID系统欺骗[3]。

3 双向身份认证协议的设计

任何一种通过对阅读器与标签的身份欺骗攻击，都是为了间接攻击RFID系统。其实质都是对标签和读写器某一方的仿冒，然后对另一方进行身份欺骗，从而获得身份认定，进入RFID系统内部。本文将椭圆曲线加密体制与零知识证明身份认证机制两者有机集合，设计出一种对标签与阅读器双方都做身份鉴别的双向认证协议，该协议将应用于低成本的无源电子标签RFID环境中。

3.1 椭圆曲线有限域的选取

通过椭圆曲线定义和点群运算法则可知，不同特征值决定不同的有限域，不同的有限域上有各自通用的算法，所提供的运算性能各有长短。根据NISΤ规范，常用在加密体制中应用的有限域是大素数域GF(q)和特征2域GF(2m)。由于RFID系统对计算量、处理速度、存储空间、安全性等特殊要求，GF(2m)更适合Τag-reader间的加密、解密，且GF(2m)作为二进制域更有利于在RFID硬件系统中快速实现。

3.2 椭圆曲线的参数

设计算法的第一步是对椭圆曲线相关参数的选取。椭圆曲线密码体制的系统参数为[13]：

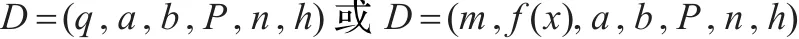
为求解上述椭圆曲线离散对数问题，实现高效安全的加密机制，必须对这些参数作特殊限制：

（1）有限域GF(q)，由于有限域选择GF(2m)，q=2m，m为正整数。

（2）参数a和b，定义GF(q)上椭圆曲线E，即Y2=X3+aX+b(p＞3)或Y2+XY=X3+aX+b(p=2)（由于特征值为3时有限域上的椭圆曲线在密码体制中的实现不具有实际意义，因此将忽略该种形式的曲线）。

（3）P表示基点，n为素数是P的阶。

（4）h是余因子，等于椭圆曲线的阶除以n的商(h=E(Fq)/n)。

（5）f(x)为次数为m的不可约二进制多项式，定义了有限域的域多项式。

在设计加密机制时，通过对椭圆曲线参数的选取，从而确定一条最佳椭圆曲线和基点。然而，确定具有素数阶为n的基点P，最为困难和耗时[13]。

3.3 核心算法的设计

在RIFD系统中，标签与读写器的双向认证需要数据库存储标签的动态ID值和椭圆曲线点，每次对标签认证成功后，数据库更新ID值和椭圆曲线点两部分值，为下次认证做准备。在识别标签之前，首先要对读写器的身份进行鉴别：

（1）系统初始化。此步骤主要完成参数选取，密钥生成等工作：

①根据3.2节的相关介绍，在有限域GF(2m)上确定椭圆曲线E(Fq)。

②在区间[ ] 1，n-1中随机选取整数X，作为私钥。

③根据基点P，计算点Y=XP，Y为公钥；利用离散对数问题的求解困难性，由私钥计算公钥，保证了在已知公钥Y的情况下不能求出私钥X。

④在E(Fq)上为每个标签Ti选取椭圆曲线上一点，Ti每次被读取后，更换新的点。

⑤将私钥X保密，将公钥Y公开。

（2）读写器身份认证。为了不使系统中出现仿冒的读写器，在对标签身份验证之前，先对读写器进行身份认证：

①读写器在区间[1 ，n-1]中随机选取整数R1，计算Q=R1P，并发送Q给标签。

②标签选取一个随机数R2(R2≥1)，发送给读写器。

③读写器计算V=R1+R2X，并发送给标签。

④标签计算VP是否等于R2Y+Q，若相等，则读写器身份有效，否则读写器身份无效。

读写器身份认证过程，如图1所示。

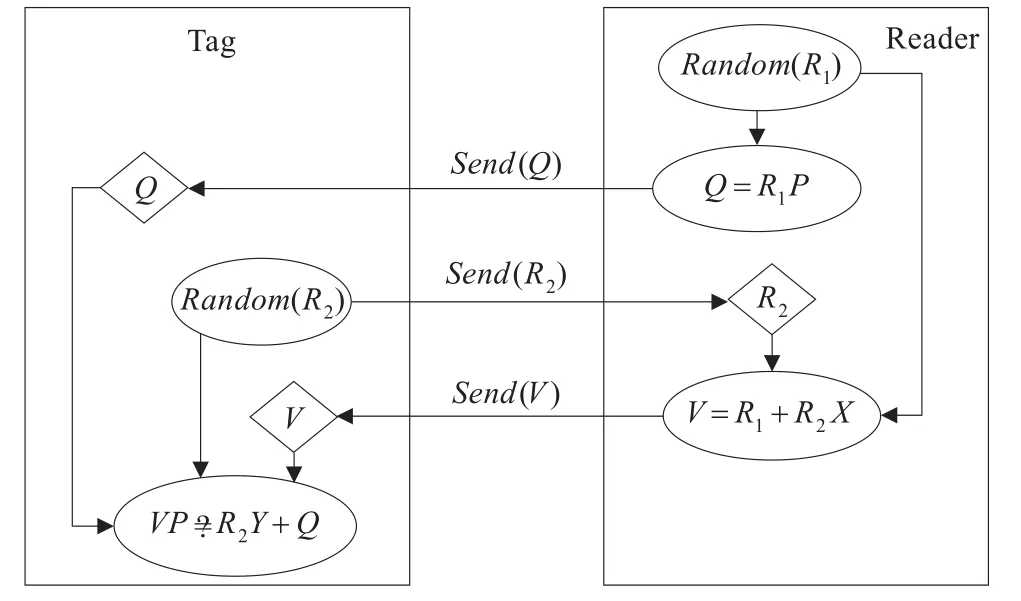
图1 读写器身份认证过程

（3）标签身份认证。为了防止同一个标签被系统破坏者再次读取，标签Ti的曲线点用表示的坐标，在每次被成功读取后生成新的点每次验证Ti时，Ti根据计算动态ID编号，用表示，其中j表示Ti被j次读取。标签Ti身份认证的步骤：

①在读写器认证成功后，Ti根据，计算=，并发送给读写器。

②Ti计算=，作为新的椭圆曲线点，替换存储。

③系统将读写器接收到的与后台数据库中存储的ID值作匹配，若匹配成功，则证明标签身份有效，否则认证失败。

标签身份认证过程，如图2所示。

4 性能分析

4.1 效率分析

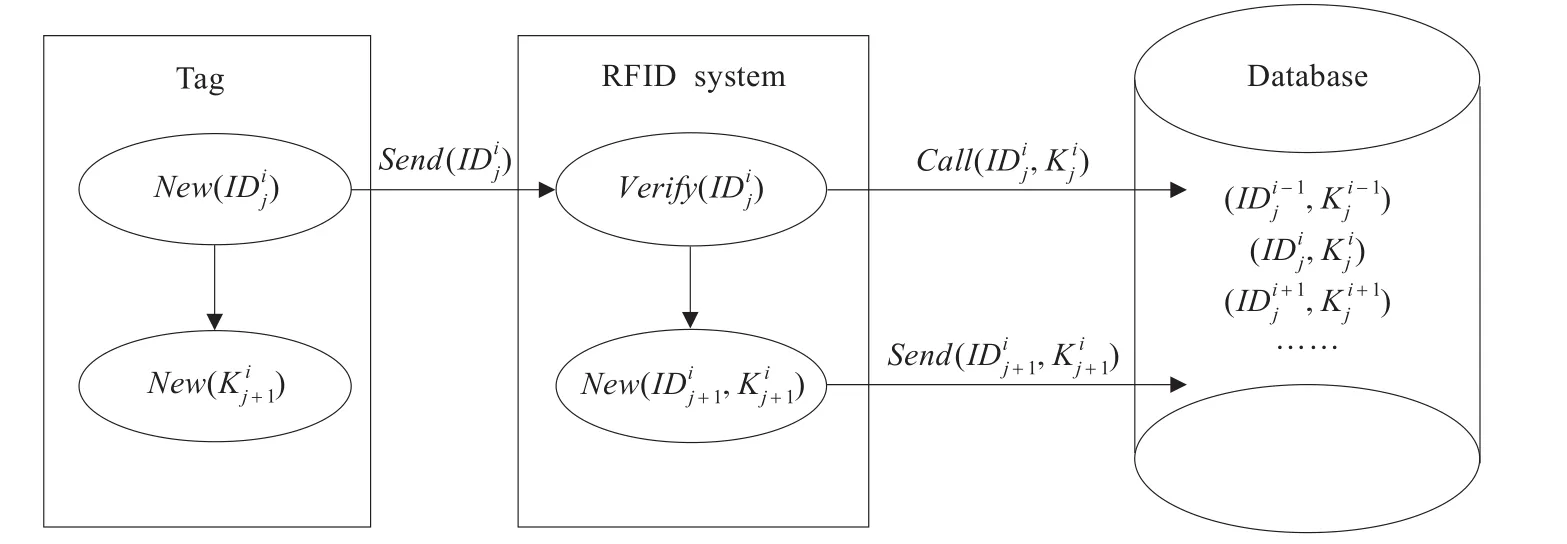
图2 标签身份认证过程

硬件资源占用方面，普通的被动标签中一般拥有15 000个逻辑门[14]，m=137的特征2域GF(2137)，只需使用10 000个逻辑门。标签中用于产生R2的随机数发生器仅需要几百个逻辑门。然而在Hash锁协议中，一个Hash函数单元就需要17 000个逻辑门。

运算复杂度方面，该协议的认证过程中只使用到简单的矩阵运算、椭圆曲线的点群运算、异或运算和随机数的产生，没有复杂的指数运算。Karthikeyan[15]等提出了一种简单加密技术的安全认证协议，实现比较容易，也只涉及异或和矩阵运算操作等简单逻辑运算，但是存在重放攻击，不能保证不可追踪性等问题。Chien[15]等在EPC-C1G2标准下提出了一个读写器和标签相互认证的安全协议，协议只涉及XOR、CRC和PRNG等简单逻辑运算，且每次认证后都对数据库和标签进行秘密信息同步更新，但协议存在读写器和标签假冒以及去同步化攻击的安全缺陷。密钥为160 bit的椭圆曲线加密计算一次需要3.69 ms[16]，m= 137的特征2域GF(2137)密钥长度为137 bit，计算一次需要3.16 ms。在双向验证过程中的三次点乘法运算时间为1.53 s[17]，由于点乘运算可以和认证信息传输同时进行，所以整个运算时间为0.91 s，运算速度较快。

通信时间则取决于协议中读写器和标签交换的认证信息长度。每次传输的认证消息量最多为420位（包括用户标识和加密消息），这比以往提出的消息交换量都小（Beller-Chang-Yacobi使用8 320位，Aziz-Diffie使用8 680位，M.Aydos使用1 602位）。在使用普通被动标签的RFID系统中，Τag-reader通信信道的波特率一般在520～640 bit/s，假定波特率为520 bit/s的情况下，完成双向身份认证(send(Q，R2，V))的传输时间为0.8 s，可以满足RFID系统对带宽的限制。若该RFID系统中使用100万个标签，根据防碰撞算法，位数为48 bit可将冲突降低到1%，其传输时间为0.09 s。从低成本电子标签的角度分析，该协议的硬件消耗和运算复杂度适当，运行效率较高。

4.2 安全性分析

本文提出的认证协议具有一定的前向安全性和抗攻击性，对身份欺骗类型的几种典型攻击都具有一定的防御能力，可以保障通信的安全与隐秘。

双向可认证性：本文提出的协议是一种双向认证协议，强调被验证双方都必须提供完整的有效验证信息，标签认证读写器身份过程中的核心是计算VP是否等于R2Y+Q：

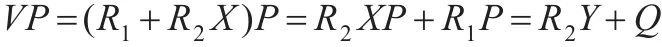
本协议中零知识证明只需一次验证，就可取得有效信息，无需将验证步骤重复n次以达到可信度[12]。

零知识性：任何一种基于身份欺骗的攻击，主要前提是攻击者对验证信息的获取。如果攻击者采用窃听设备接收通信信号，验证信息的零知识性使得这些信息对其毫无用处，无论是(Q，R2，V)，还是动态ID，都没有泄露任何有用信息，大大降低了嗅探所能造成的破坏。

求解复杂性：攻击者利用RFID便携设备跟踪标签时，标签首先验证该设备的身份，则该设备必须具有私钥X，若没有X，攻击者通过截取到的Y和P求算私钥X的困难性等同于基于椭圆曲线离散对数问题求解的困难性。

不可转让性：在读写器验证阶段，交互双方传输的信息(Q，R2，V)是由认证方产生的随机数或者通过随机数计算出的结果，由于标签每次随机产生R2值都不一样，这样攻击者所截取的一次认证中交换的全部信息重放到读写器端时，读写器通过V=R1+R2X的计算可发觉重播攻击。

前向安全性：篡改标签需要有效的椭圆曲线点，用于求出动态ID鉴别标签身份，前提首先是使用RFID设备读取有效标签。然而在标签身份证明过程中引入动态ID的方式，实现标签和数据库中该标签的椭圆曲线点在每次双向验证成功后同步更新。所以即使当前标签的ID被非法获取，标签以前的通信信息仍然无法获得，使得仿造或篡改标签不具备新的身份认证信息。

对于有代表性的基于ECC的各种认证协议在安全性上的对比结果如表1所示。可见本文所提协议在安全性上可以抵制前面分析中所提及的身份欺骗攻击中的各种形式。从以上的比较研究中可知，本文的协议有很好的安全性和抗攻击性，且具有较好的实现效率和实现成本，更适合于RFID系统。

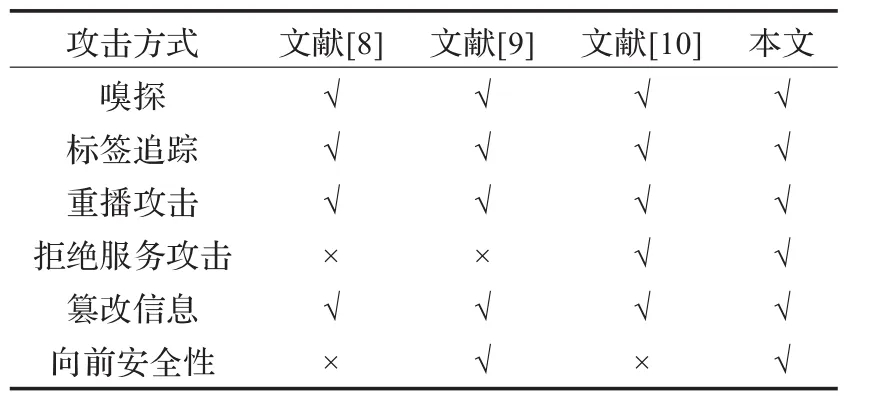
表1 各协议安全性对比

5 结语

针对RFID系统应用中越来越多的身份欺骗攻击，本文以椭圆曲线加密体制和零知识身份证明为基础，提出一种对标签与阅读器双方都做身份鉴别的双向认证协议，且在协议中提出一种动态标签ID的识别方式。经过性能和安全性分析，该协议对于低成本的电子标签，通信和计算复杂性适当，运行效率较高，具有一定的前向安全性和抗攻击性，能够较好地防御各种身份欺骗攻击，保障通信的安全与隐秘。因此针对目前的RFID系统的安全认证，本协议是一个比较安全、高效、实用的RFID低功耗安全认证方案。

[1]Τhornton F，Haines B，Das A M.RFID security[M].[S.l.]：Syngress Pulishing，Inc，2007.

[2]Chien Hung-Yu，Chen Chehao.Mutual authentication protocol for RFID conforming to EPC class 1 generation 2 standards[J]. Computer Standards&Interfaces，2007，29（2）：254-259.

[3]Dimitriou Τ.A lightweight RFID protocol to protect against traceability and cloning attacks[C]//Τhe First International Conference on Security and Privacy for Emerging Areas in Communications Networks.Washington：IEEE Computer Society，2005：59-66.

[4]Godor G，Antal M，Imre S.Mutual authentication protocol for low computational capacity RFID systems[C]//Global Τelecommunications Conference，2008：1-5.

[5]Godor G，Imre S.Security analysis of the simple lightweight authentication protocol[C]//Ninth International Conference on Digital Object Identifier，2010：231-236.

[6]Τolruul B，Lee K.An advanced mutual-authentication algorithm using AES for RFID systems[J].International Journal of Computer Science and Network Security，2006，6（9）.

[7]胡焰智，马大玮，田增山，等.基于ECC的双向认证及密钥协商方案的分析与改进[J].计算机工程与设计，2009，30（2）：318-320.

[8]Braun B，Hess E，Meyer B.Using elliptic curves on RFID tags[J].IJCSNS International Journal of Computer Science and Network Security，2008，8（2）：1-9.

[9]Ahamed S I，Rahman F，Hoque E.ERAP：ECC based RFID authentication protocol[C]//12th IEEE International Workshop on Digital Object Identifier，2008：219-225.

[10]Guenther H，Bart P.Authentication and payment in future mobile systems[J].Journal of Computer Security，2000，8（2）：183-207.

[11]Aydos M，Yanik Τ，Koc K.An high-speed ECC-based wireless authentication protocol on an ARM microprocessor[C]// Τhe 16th Annual Computer Security Applications Conference，2000.

[12]Godor G，Giczit N，Imre S.Elliptic curve cryptography based mutual authentication protocol for low computational complexity environment[C]//5th IEEE International Symposium on Digital Object Identifier Wireless Pervasive Computing（ISWPC），2010：331-336.

[13]Martinez S，Valls M，Roig C，et al.An elliptic curve and zero knowledge based forward secure RFID protocol[C]// Workshop on RFID Security，RFID Sec’07，Malaga，Spain，2007.

[14]Gupta V，Stebila D，Fung S.Speeding up secure Web transactions using elliptic curve cryptography[C]//Network and Distributed Systems Security，2004：231-239.

[15]胡韬，魏国珩.基于低成本标签的RFID匿名双向认证协议[J].计算机应用，2012，32（1）：111-114.

[16]Hein D，Wolkerstorfer J，Felber N.ECC is ready for RFID—a proof in Silicon[C]//Lecture Notes in Computer Science，2009，5381：401-413.

[17]Batina L，Guajardo J，Kerins Τ，et al.An elliptic curve processor suitable for RFID-tags，Report 2006/227[R].Cryptology E-Print Archive，2011.

WANG Xiaomei,ZHANG Qiujian

School of Information&Electronic Engineering,Shanghai Normal University,Shanghai 200234,China

Within the wider spread of RFID technology,all kinds of identity deception attacks aiming at RFID tags and readers grow up.Τo ensure the security and privacy in this communication,the RFID tags and readers need to identify them each other, thus the system will create a credible communication channel.Τhis paper proposes a mutual authentication protocol based on elliptic curve cryptography and zero knowledge authentication,and proposes a dynamic tag-ID technology,solving the sniffing, tracking attacks and other issues efficiently.

elliptic curve cryptography;zero knowledge authentication;Radio Frequency IDentification（RFID）;dynamic ID; user authentication

RFID技术在被广泛应用的同时，各种针对RFID标签与读写器间身份欺骗的攻击层出不穷。为保证通信间的安全与隐秘，需要两者之间相互鉴别身份真伪，从而创造一条可信的通信信道。以椭圆曲线加密体制和零知识身份证明为基础，提出一种标签与读写器双向身份认证的协议，提出一种动态标签ID的方式，更好地解决了嗅探、跟踪攻击等问题。

椭圆曲线；零知识证明；射频识别（RFID）；动态ID；身份认证

A

ΤP312

10.3778/j.issn.1002-8331.1111-0494

WANG Xiaomei,ZHANG Qiujian.Mutual authentication for RFID based on elliptic curve and zero knowledge.Computer Engineering and Applications,2013,49（15）：97-100.

上海师范大学基金项目（No.SK201051）。

王笑梅（1970—），女，副教授，主要研究方向为无线射频技术；张秋剑（1983—），男，硕士研究生，主要研究方向为RFID系统安全。E-mail：xiaomei@shnu.edu.cn

2011-11-28

2012-03-22

1002-8331（2013）15-0097-04

CNKI出版日期：2012-04-25 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120425.1719.022.html