基于Julia分形集的模运算图像加密算法研究

孙媛媛，陈丽娜，朱书敬

大连理工大学 计算机学院，辽宁 大连 116024

基于Julia分形集的模运算图像加密算法研究

孙媛媛，陈丽娜，朱书敬

大连理工大学 计算机学院，辽宁 大连 116024

SUN Yuanyuan,CHEN Lina,ZHU Shujing.Research on modulo image encryption algorithm utilizing Julia sets.Computer Engineering and Applications,2013,49（15）：75-79.

1 引言

图像加密是图像安全保护的直接有效的技术手段。传统的数据加密算法多数针对文本数据或二进制数据，通常具有较高的计算复杂度。由于图像数据具有编码结构特殊、数据量大、实时性要求高等特点，传统的数据加密算法直接用于图像数据加密，很难满足实时性要求，而且会改变数据格式等，这就要求对图像数据要采用特殊的加密算法。因此在多媒体技术应用日益广泛的今天，研究图像加密具有重要的理论和现实意义。

目前对图像加密的方法主要有图像置乱、结合其他数据处理技术加密和利用密钥加密几种。在图像置乱算法中，有根据某种变换规则进行置乱的算法，如邵利平等基于高维矩阵变换构造了雪崩图像置乱变换[1]；还有根据图像本身特点进行置乱的算法，如江南等对图像采用先分块置乱再根据DCΤ变换进行二次置乱的方法[2]。在结合其他数据处理技术方面，Zeng等人将加密算法融入到压缩过程中[3]。采用密钥加密的算法中，有很多关于混沌密码学的研究，如陈关荣等人基于三维混沌映射产生密钥，对图像进行异或运算进行加密[4]。

另外，近年来人们在分形理论结合加密算法方面做了很多工作，如刘文涛等利用分形图的不规则性，将明文放入分形图中并通过控制子图的旋转得到密文[5]。还有直接用分形集作密钥的算法，如Rozouvan用Mandelbrot集作为密钥加密图像[6]。

本文采用的方法即是利用分形集为密钥，对分形图像进行密钥转换，将原文与密钥进行模运算之后，在图像上进行扩散的加密算法。本文采用的Julia分形集是分形中的经典集合，可以由几个参数迭代产生，这使得密钥更易于存储传输。同时，Julia集具有无限性以及混沌特性，迭代参数的微小变动都将导致密钥的变化，使得算法能够有效抵御密钥攻击。另外，扩散算法使得明文中任意一个像素值的改变都能导致整个图像像素值的改变，对选择明文攻击具有较强的抵御性。本文采用的加密算法直接将模运算应用于图像加密，实现起来简单有效。

2 加密算法描述

2.1 以Julia集为密钥的加密过程

Julia集是分形中的经典集合，国内外学者对其拓扑结构特性进行了深入分析[7-9]。本文以映射f(z)=zw+c(c=p+qi，w，p，q∈R)构造复平面广义Julia集。研究表明，Julia集J(f)是多项式f的斥性周期点的闭包。Julia集有很多性质，其中重要的一点是f在Julia集上是混沌的，也就是f在Julia集上对初始条件有敏感的依赖关系[10]。作为分形集，Julia集边界有无限迭代自相似性和精细的嵌套拓扑结构，因此均是在边界选取Julia图像进行放大，以构造密钥，然后进行密钥转化。由于Julia集图像是由复平面上的点映射到图像上，因此选取Julia集边界时，先选择图像上复杂的边界区域，然后转为复平面的区域，最后将选取的部分复平面区域重新映射到图像上。Julia集加密的密钥分别由复平面上的区域范围Xmax，Xmin，Ymax，Ymin（Xmax，和Xmin为X轴上的最大值和最小值，Ymax和Ymin是Y轴上的最大值和最小值，Xmax，Xmin，Ymax，Ymin均为实数），以及Julia集参数w，p，q等共七个密钥。

本文采用的加密算法是基于模运算的对称密钥加密算法。为方便起见，定义R，G，B为矩阵，代表原图像的每一层。此外，矩阵Rkey，Gkey，Bkey代表密钥的每一层，均为m×n维。转化后的密钥矩阵为R′，G′，B′，转化过程如公式（1）所示：

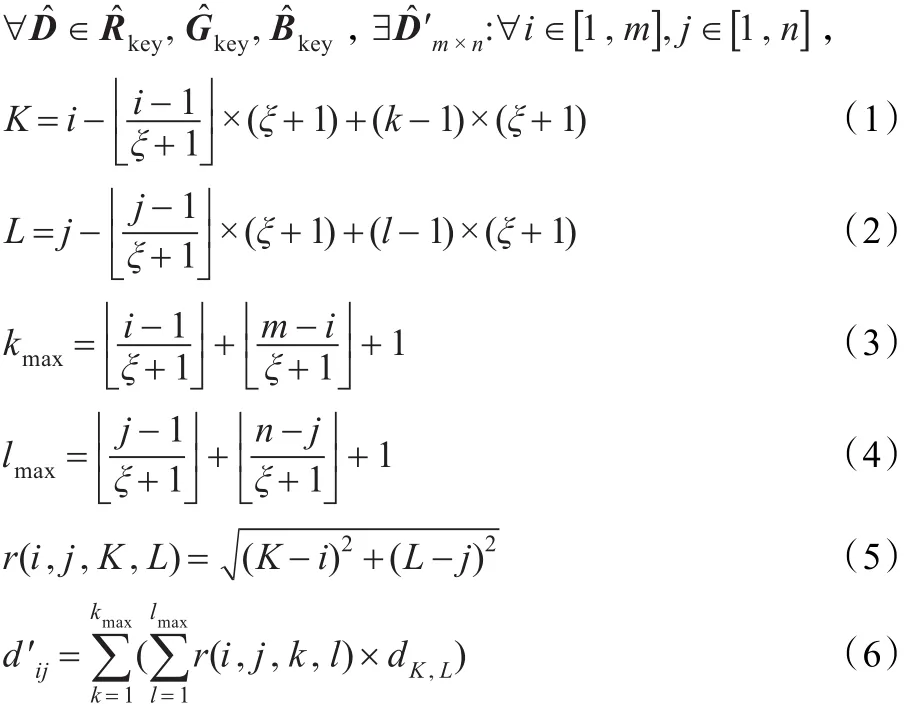
其中，(i，j)为当前像素点坐标，(K，L)为经过式（1）～（4）计算的坐标，k，l，kmax，lmax，为求坐标K，L所用中间变量。坐标(K，L)与坐标(i，j)的像素点间的横向或纵向距离为ξ的整数倍，ξ表示两个像素点之间相隔数，取值范围为[0，max(m，n)-2]。式（5）中r(i，j，k，l)为坐标(K，L)与坐标(i，j)的像素点间的距离，式（6）中d′ij为坐标(i，j)处像素点经过密钥转换后得到的密钥值，dK，L为坐标(K，L)处的像素值。参数ξ的引入主要是对Julia集密钥起到一定程度的置乱作用，使得加密后的图像有更强的置乱效果。同时使得转化后密钥的每个像素点的值与整个图像内所有与该点相距ξ个像素点的值都有关，这使得原始Julia集密钥任意点像素值的变化将导致转化后的密钥的巨大变化，因此大大增强密钥的健壮性。得到密钥后，加密过程如公式（7）所示。

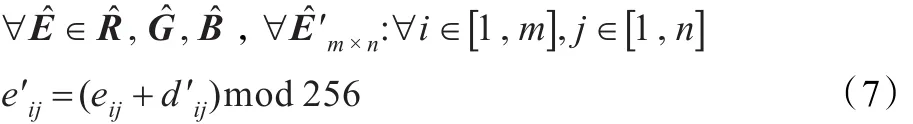
其中，eij为待加密图像(i，j)处像素值，e′ij为加密之后对应坐标(i，j)处像素值，d′ij为Julia集(i，j)处转化之后的密钥值。

解密时先对密钥进行转化，再利用公式（8）进行解密。

由于模运算的特点，解密图像和原始图像完全一样。

2.2 扩散算法

扩散算法最初由Shannon提出，Shannon最初把扩散过程用于通信中，通过求几个数的平均值来得到密钥值[11]。扩散也是图像加密中一种重要的方法。本文提出的扩散算法是以单个像素值为单位，在图像的三个图层之间，先对R图层扩散，然后再对G图层扩散，最后扩散的是B图层。为了保证扩散过程能影响到图像的每一个像素值，本文所采用的扩散算法是先在每一行上对三个图层按顺序进行扩散，然后在每一列上进行相似的操作。这样每一轮扩散之后图像就有很好的扩散效果。

本文采用的扩散公式如公式（9）所示：

其中qi、qi-1是密文的当前像素值和当前像素的前一个像素值。对应的，pi、pi+1是明文的当前像素值和当前像素的前一个像素值。对于24位位图的每个通道是8位，则l取值为256。由于图形扩散是顺序进行的，所以每一次扩散结束后的值可以作为下一次扩散的初始值，即q0=。其中扩散的第一个密文像素值q0和明文的最后一个像素值，为扩散阶段的密钥。

2.3 算法加密过程描述

本文的算法加密过程大概分为以下几个步骤：

（1）产生Julia集图像，选取局部边界并放大为256×256图片；

（2）对Julia集图像进行密钥转化；

（3）对明文进行第一次加密，得到密文；

（4）根据扩散密钥pi+1，qi-1进行扩散；

（5）若需要进行多次迭代，可以重复步骤（4）；

（6）得到最终密文图像。

加密流程框图如图1所示。

图1 加密流程框图

2.4 算法解密过程

由于本文提出的算法是对称算法，所以算法解密过程按加密过程逆序进行即可，注意迭代也是逆序的。在解密过程中，要确保每一次解密密钥都与对应的加密密钥一样。

3 实验结果与算法分析

3.1 实验结果

现以一幅256×256的Lena标准彩色图进行加密为例。该算法采用的标准彩色图像为24位彩图，即每24位二进制值表示一个彩色图像像素值，每个像素值由RGB 3个通道组成，内存中24位二进制代表的颜色通道顺序为BGR，即每8位表示一个颜色通道。由f(z)=zw+c产生Julia集，其中w=15，c=p+q×i，p=0.5，q=-0.7，为Mandelbrot集的第二周期点。横向扩散密钥为R层中q0=10，B层pi+1= 142。纵向扩散密钥为R层q0=100，B层pi+1=222。为了保证密钥的健壮性，对图像进行了两轮加密，第二轮加密的横向扩散密钥为R层中q0=11，B层pi+1=210。纵向扩散密钥为R层q0=200，B层pi+1=20。原图加密并进行两次扩散后得到的密文分别如图2和图3所示。

图2 Lena图

图3 加密后图像

3.2 密钥分析

本文提出的算法密钥空间由Julia集密钥（包括构成Julia集图形的参数，密钥转化时图像像素值间隔ξ，选取图像的范围，扩大倍数等都可以作为密钥），扩散密钥共同组成。密钥空间为Julia集密钥，ξ与扩散密钥的乘积。Julia集密钥为(Xmax，Xmin，Ymax，Ymin，w，p，q)，扩散密钥为(pi+1，qi-1)。那么密钥空间S=ξ×(Xmax×Xmin×Ymax×Ymin×w×p×q)×(pi+1×qi-1)。该算法中，Xmax，Xmin，Ymax，Ymin，w，p，q均为double型，计算机内存中double型为8个字节即64位，故每一个密钥所需空间为264。ξ取值范围为0～255，即28。扩散密钥范围为0～255，则空间为28。可以得到密钥空间为S=2(64×7+8)×(28×2)k=2456×(216)k，其中，k(k=1，2，…)为迭代次数。在Rozouvan提出的算法中，Julia集参数和ξ共同构成了密钥，同理密钥空间为2200。可见本文的密钥空间比较大，能更好地抵御密钥攻击。图4所示为Julia集图像，图5所示为取一块区域放大10 000倍后图像。

图4 Julia集图像

3.3 密钥敏感性分析

图5 局部放大的Julia集图像

在本文的加密过程中，一共涉及到两个过程的密钥，分别是Julia集密钥和扩散密钥。Julia集密钥分别是Julia局部扩大的边界密钥，参数w，p和q值。在解密过程中，任意改变一个密钥值，则Julia集图像转化之后的密钥均不能正确解密。

以文中的w值为例，改变w=15的值为w= 15.000 000 000 1，在解密时候，用改变的w值产生的密钥去解密原w值加密的密文。如下各图所示，图6为未改变w值加密得到的密文，图7为改变w值后得到的密文，比较图6和图7的像素值可知，两个图片的R、G、B层分别有99.609%、99.615%、99.627%的像素值不同。图8为正确密钥解密得到的图像，图9为改变w值后解密得到的图像。由图9可知，Julia集密钥对极微小的改变都有很高的敏感性。

图6 未改变m值的加密密文

图7 错误密钥得到密文

图8 正确密钥解密得到图像

图9 错误密钥解密得到图像

本文密钥采用Julia集映射生成，表1为测试Julia集参数的敏感性结果。

表1 Julia集参数敏感性

本文在相同的软件平台下实现了Rozouvan算法。Rozouvan算法所用分形集映射为Zn+1=+b×z0(z0为复

平面上的点，b=rp+rq×i,rp,rq∈R)。表2为测试Rozouvan算法的密钥敏感性结果。

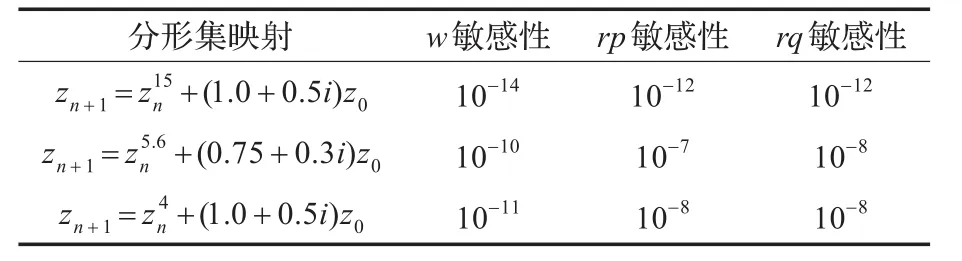
表2 Rozouvan算法密钥敏感性

表1和表2的实验结果表明，本文采用Julia集映射生成的密钥图像具有较高的敏感性。

扩散过程的密钥主要为横向迭代和纵向迭代时的R层qi-1和B层pi+1，共四个密钥值。仅改变其中一个密钥值，得到的加密图像就和原密钥加密图像有很大的不同。例如改变第一轮迭代时横向扩散R层密钥qi-1值为11，得到的加密图像三个图层（测试时候顺序依次为R、G、B）与原来密钥得到的加密图像的三个图层分别有99.21%，99.21%，99.22%的像素值不同。

较之于Rozouvan算法，本文采用了Julia集为映射生成密钥，敏感性较好。增加的扩散密钥，进一步提高了密钥敏感性。

3.4 明文敏感性分析

本文加密算法能够很好地抵抗选择明文攻击，扩散算法使得明文的任何一个像素值的改变，都能影响到密文的像素值。Lena彩色图坐标（100，105）处的像素值为（186，139，124），改变R图层的灰度值186为185，加密之后通过比较计算得到两个加密图像R层图像有99.63%的像素值不同，G层图像为99.63%，B层图像为99.59%。由此可见，原图像任意一个图层像素值的改变，就会影响到其余图层，进而密文图像不能正确解密。

在Rozouvan实验中，同样改变原图同一个像素值，得到的密文中只有R层一个像素值不同，其余都相同。这说明了本文中的扩散方法能够很好地抵御对明文的攻击。

3.5 直方图分析

本文对图像直方图的分析采用MAΤLAB 7.0平台，实验证明采用本文算法加密之后的密文图像每一个图层的灰度分布比较均匀。实验分析仍然采用前面的参数。明文图像和密文图像三个图层的直方图分别如图10、图11所示，其中横坐标代表灰度级，纵坐标代表该灰度级在图像中出现的频率。通过实验得知，密文图像的灰度值分布比较均匀，说明该算法的扩散过程比较有效，并且在很大程度上改变了原图的统计特性。

对直方图的分析仍然采用的是上面一组密钥值，明文图像采用Lena真彩图，与得到的密文图像的RGB三个图层的比较如下图所示。图10为加密原图以及原图三个图层的直方图。图11为加密之后密文图像已经对应的单个图层的直方图。

由实验结果得知，加密之后图像每个图层的灰度值趋于均衡，说明图像灰度扩散效果比较好。

3.6 相邻像素相关性分析

图10 原图直方图

图11 加密图直方图

相邻像素相关性系数可以验证一个算法对图像的置乱程度。相关系数越小，说明图像像素间的相关性越好；反之相关系数越大，那么相关性也就越差。计算表达式为：

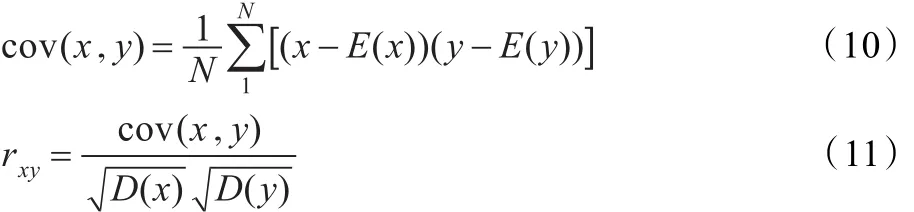
其中N表示选取的像素值个数，x和y分别表示相邻像素的像素值。rxy为相邻像素的相关系数。本文在水平、竖直和对角方向分别随机选取了1 000对相邻像素进行分析，如表3所示。通过实验可以验证原图像经过加密之后得到的密文，其相邻像素的相关系数很小，说明达到了很好的置乱效果。

4 结论

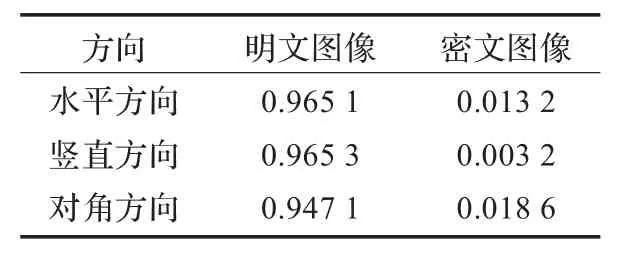
表3 相邻像素相关系数

Rozouvan提出的以Mandelbrot分形集为密钥的密钥转换方法，无法有效抵御选择明文攻击，本文在Rozouvan的图像加密算法基础上，采用对初始值更为敏感的Julia分形集为密钥，并且在算法中添加了扩散方法，得到以下结论：

（1）丰富的Julia集密钥可由较少参数产生，大大减少了密钥存储空间。

（2）Julia集特有的边界混沌特性，使得密钥对参数的轻微变化非常敏感，从而大大提高了加密算法的安全性。

（3）本文在Rozouvan基础上提出的改进算法，添加了扩散方法，有很好的置乱效果，该算法具有更大的密钥空间，明文和密钥敏感性更好，尤其增强了对选择明文攻击的抵御性。

综上所述，该算法密钥存储空间小，计算简单，加密速度快，对原图像无损坏，下一步工作可就密钥转换作进一步改进。

[1]邵利平，覃征，衡星辰，等.基于高维矩阵变换的雪崩图像置乱变换[J].中国图象图形学报，2008，13（8）：1429-1436.

[2]江南，张帆，刘文予.适合于网络传输的二次置乱图像加密算法[J].中国图象图形学报，2009，14（5）：897-904.

[3]Zeng W，Lei S.Efficient frequency domain selective scrambling of digital video[J].IEEE Τransactions on Multimedia，2003，5（1）：118-129.

[4]Chen G R，Mao Y B，Chui C K.A symmetric image encryption scheme based on 3D chaotic cat maps[J].Chaos，Solitons and Fractals，2004，21（3）：749-761.

[5]刘文涛，孙文生.分形理论在密码算法中的应用[J].中国电子科学研究院学报，2008，3（6）：580-585.

[6]Rozouvan V.Modulo image encryption with fractal keys[J]. Optics and Lasers in Engineering，2009，47（1）：1-6.

[7]范延军，孙燮华，邓林涛.高阶Garotid-Kundalini函数Julia分形集的特性[J].计算机工程与应用，2006，42（1）：86-88.

[8]Wang X Y，Sun Y Y.Τhe general quaternionic M-J sets on the mappingz←zα+c(α∈N)[J].Computers and Mathematics with Applications，2007，53（11）：1718-1732.

[9]Blokh C，Curry L，Oversteegen A.Locally connected models for Julia sets[J].Advances in Mathematics，2011，226（22）：1621-1661.

[10]法尔科内.分形几何——数学基础及其应用[M].曾文曲，译.2版.北京：人民邮电出版社，2007：194-200.

[11]Shannon C E.Communication theory of secrecy systems[J]. Bell System Τechnical Journal，1949，28.

SUN Yuanyuan,CHEN Lina,ZHU Shujing

College of Computer Science and Τechnology,Dalian University of Τechnology,Dalian,Liaoning 116024,China

As an important field in information security,image encryption algorithm has been a research focus.A novel image encryption algorithm combining with features of the classic fractal Julia sets is proposed.Τhis algorithm utilizes Julia set to generate the random key and modulo operation method is used for image encryption,and then diffusion process is used twice to generate the encrypted image.Since Julia sets can be generated with only a few parameters,it can reduce the storage space greatly. In addition,Julia sets have infinite structures and chaotic properties.Even the slight disturbance of the parameters can change the key dramatically,which will lead to the wrong decryption of the image.Τhe experimental results show that the algorithm has lager key space and more sensitivity for the key compared to the algorithm proposed by Rozouvan utilizing the Mandelbrot sets as the key.In particular,it can resist chosen-plaintext attack more efficiently.

Julia sets;modulo operation;diffusion;image encryption

作为信息安全的重要领域，图像加密算法一直是人们研究的热点。针对经典分形集合Julia集的特点，提出一种图像加密算法。将Julia集作为一种随机元素生成密钥，采用模运算方法对图像进行加密，对生成的密文进行两次扩散，得到最终密文。由于Julia集密钥仅需几个参数就可以表示，大大减小了存储空间。并且Julia集的无限性以及混沌特性使得任意参数的极其微小的变动都将导致密钥剧烈变化，无法正常解密。该算法较Rozouvan提出的以Mandelbrot分形集为密钥的转换方法，密钥空间更大，密钥敏感性显著提高，尤其能够有效抵御选择明文攻击。

Julia集；模运算；扩散；图像加密

A

ΤP751

10.3778/j.issn.1002-8331.1203-0071

国家自然科学基金（No.61103147，No.61075018）；中央高校基本科研业务费专项资金（No.DUΤ12JB06）。

孙媛媛（1979—），女，博士，副教授，主要研究领域为分形理论及应用，复杂网络理论；陈丽娜（1985—），女，硕士研究生。E-mail：syuan@dlut.edu.cn

2012-03-05

2012-06-20

1002-8331（2013）15-0075-05