利用Excel实现明渠特征水深计算

丁丽泽,欧阳明,章晴雯

(1.嘉兴职业技术学院,浙江嘉兴 314036;2.浙江工业大学建筑工程学院,浙江杭州 310014)

利用Excel实现明渠特征水深计算

丁丽泽1,欧阳明2,章晴雯1

(1.嘉兴职业技术学院,浙江嘉兴 314036;2.浙江工业大学建筑工程学院,浙江杭州 310014)

针对正常水深、临界水深、收缩水深和共轭水深这四种明渠特征水深,通过Excel软件的填充柄、单变量求解功能、循环引用迭代计算和规划求解功能四种方法进行求解计算。通过实例计算以及与文献计算结果对比分析,表明Excel求解与一般的人工手算或计算机编程计算相比,能更快速、准确、方便地求得各种断面形式的水深,计算过程方便易懂、计算结果精确可靠,为教学和设计等提供了很好的方法和思路。

明渠;特征水深;Excel;高次方程

在明渠水力学中,正常水深、临界水深、收缩水深和共轭水深被称为渠道的特征水深,在近些年来已有许多学者进行了研究并提出了诸多的计算方法。芦琴[1]比较系统地介绍了多种断面明渠特征水深的直接计算方法,给出了较为常见的明渠特征水深直接计算公式的比较和误差分析与评价;而李蕊[2]系统地分析了梯形明渠特征水深的直接计算方法并在此基础上进行了一定的改进从而提出了四套相应水深的计算公式。正如文献[1]和[2]中提到的,明渠特征水深的求解实质上是求解含多个未知参数的单变量或多变量的超越方程或高次方程;而这些方程在理论上多是没有解析解的,因此在实际的应用中常采用试算法、迭代法、图解法和近似解法等。随着研究的不断深入,迭代算法和直接计算公式成了研究的主流方向[1-11],特别是直接计算公式的推求在近些年来已成为研究热点[6-11]。在目前的文献报道中,特征水深计算算法的实现除了常规的迭代求解和最小二乘法计算外,还包括牛顿算法[11]、遗传算法[12]、模式搜索算法[13]、粒子群算法[14-15]、蚁群算法[16]、群竞争算法[17]等。然而这些方法的实现通常均需借助计算机实现,除了直接应用编程软件进行程序编写实现[18],近年来更倾向于利用数值计算软件来求解,特别是MATLAB的使用[19-20]。然而无论是进行编程还是利用MATLAB实现,对于一般的工作人员和使用者而言均不易掌握,需要进行比较专业性的学习,且在实际的运用中往往需要进行一定的调试,特别是利用编程实现则更需要书写繁复的程序代码和集成开发,这就更增加了推广应用的难度。在日常生活和工作中,Excel软件作为最常用的基本办公应用软件之一,其在数值计算上也具备很好的功能,用Excel求解明渠特征水深在理论上是可行的,而且这样也可以避免必须安装相关的专业软件。

1 四种常见水深的基本计算公式

1.1 正常水深的计算

正常水深即为明渠恒定均匀流水深[2],通过联立恒定流的连续方程和谢才公式可以得到明渠均匀流的流量公式,再将曼宁公式代入可以很方便地得到明渠均匀流的基本方程:

式中:n为渠道粗糙系数;Q为流量;i为渠道比降;A为渠道过水断面面积;χ为湿周。

由于过水断面面积A和湿周χ在进行计算时均包含正常水深h0,而不同形式的过水断面具体计算公式有所不同。若将相应的面积和湿周这些水力要素代入可以得到包含正常水深h0的隐式方程计算式,该方程是一个高次方程,不能直接求得正常水深h0的解析解。

1.2 临界水深的计算

与正常水深有所不同的是临界水深、收缩水深和共轭水深都属于明渠恒定非均匀流水深[2],而临界水深相应于断面单位能量最小值的水深,以hk表示[21]。通过计算断面比能Es并对水深求导使其等于零可以求得临界水深满足:

式中:α为动能修正系数,通常取作1.0;Q为明渠流量;g为重力加速度,通常取为9.81 m/s2;AK为相应于临界水深时的过水面积;BK为相应于临界水深时的水面宽度。

同求解式(1)一样,式(2)含有AK和BK,这都与临界水深hk有关,将具体断面的水力要素代入也会得到一个高次方程,该方程除了某些简单的断面形式(如矩形断面),一般也没有解析解。

1.3 收缩水深的计算

一般地,收缩水深在工程中最常见于泄水建筑物下游收缩断面,该处流速最大,水深最小,以hc0表示,收缩水深hc0要小于临界水深hk[21],因此水流流态为急流。利用能量守恒原理,分别取上游断面和收缩断面列出能量方程式,可以得到:

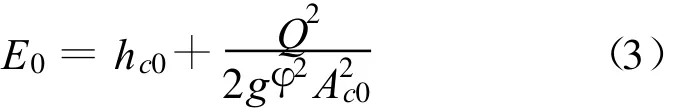
式中:E0为上游断面总水头;hc0为收缩水深;Q为过水流量;g为重力加速度,通常取为9.81 m/s2;φ为流速系数;Ac0为收缩断面面积。

显然由于某个具体的断面形式的断面面积Ac0包含有收缩水深hc0,具体的水力要素代入能得到高次方程需要求解,这在理论上同样不存在解析解。

1.4 共轭水深的计算

当明渠中水流由急流状态过渡为缓流状态,产生水面突然跃起的局部水力现象,也即在较短的渠段中水深从小于临界水深急剧地跃升至大于临界水深[21],这便是水跃,而共轭水深就发生在水跃过程中。由于水跃的上部会有表面旋滚的现象,故将表面旋滚起点的过水断面称作跃前断面,而表面旋滚末端的过水断面称作跃后断面,两个断面的水深分别叫作跃前水深(或第一共轭水深)和跃后水深(或第二共轭水深),我们将这两个水深统称为共轭水深。根据水跃前后断面的动量方程和连续性方程可以整理得棱柱体水平明渠的水跃方程:

式中:Q为流量;g为重力加速度,通常取为9.81 m/s2;A1和A2分别表示跃前和跃后过水断面的面积;hc1和hc2分别表示跃前和跃后过水断面形心点的水深。

只要将水力要素代入,当渠道断面形状、尺寸和过水流量一定,则水跃方程(4)两端仅为水深的函数,将之称为水跃函数:

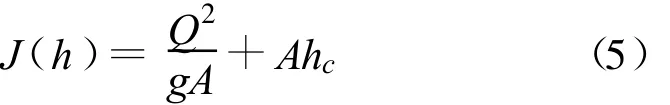
式中:A是跃前或者跃后过水断面面积;hc是跃前或者跃后过水断面形心点的水深,其它符号含义同前述。

对于共轭水深,它不同于其它3种水深,因为它共包含两个水深,它们具有相同的水跃函数值,因此将其称作共轭水深,一般是由已知的一个共轭水深h1(或h2)计算另一个未知的共轭水深h2(或h1)。除了某些简单的断面形式(如矩形断面),一般共轭水深的计算并不存在解析解。

2 水深计算的Excel求解方法

由于明渠特征水深的求解实质上是求解含多个未知参数的单变量或多变量的超越方程或高次方程,因此结合Excel本身具有的数值计算功能,在明渠特征水深的Excel求解实现上一般可以用填充柄、单变量求解功能、循环引用迭代计算和规划求解功能等来完成。

2.1 巧用拖动填充柄自动计算

拖动填充柄在Excel是非常常见的操作,一般而言,在这过程中往往需要先定义相对引用和绝对引用,这是由于在拖动填充的过程中,相对引用的单元格会随行与列变化而变化,而绝对引用就不会变化了[22],某些常数参量(如重力加速度g和计算时明确数值的流量Q等)就必须用绝对引用,否则就会发生错误,绝对引用需要在确定的行号或者列号前加“＄”符号以示区别。利用拖动填充柄进行计算的本质就是试算,通过改变需要求解的特征水深的数值得到一系列的结果再与需要求得的结果进行比较,然后缩小搜索范围直到求解出足够精度的解答。由于事先不确定待求特征水深准确的范围,只能根据经验和基本的水力学知识进行预判,这在一定程度上会增加计算量,但从另一方面来看,这种方法可以直接应用特征水深的基本方程以及公式,往往比较直观和明确,很早以前利用Excel求解非线性方程往往应用该方法。

2.2 单变量求解功能

明渠特征水深一般就只有一个,或者说未知水深只有一个,因此利用单变量求解是可行的。“单变量求解”,顾名思义,即单个变量的求解计算,可以在Excel的“工具”下拉菜单中找到,如图1所示,它适用已知公式结果但不知结果所需的输入值的情况,单变量求解是Excel通过不断改变单元格中数值直到从属于该单元格的公式返回预期结果[23]。

图1 单变量求解输入框

由于单变量求解功能的简便性,单变量求解功能在水力计算中也应用得越来越广泛,文献[24]就利用Excel的单变量求解功能进行明渠均匀流水力计算作了初步的探讨,其中就有涉及求解正常水深的环节,文献[25]也谈及利用Excel的单变量求解功能求解梯形断面渠道正常水深,但利用该功能求解其它特征水深还未有多见。虽然单变量求解方便,但它是用牛顿法以一定步长启动迭代计算,有时甚至修改迭代几千次或多次修改估计根仍然不能得到有意义的根[23]。

2.3 规划求解功能

规划求解功能与单变量求解功能相比较,其功能更为强大。当然同单变量求解一样,操作的单元格需要与工作表的公式相关联。“规划求解”可以在Excel的“工具”下拉菜单中找到,如果没有找到该选项可以在“工具”下拉菜单中“加载宏”先进行安装,再打开规划求解功能框,如图2所示。

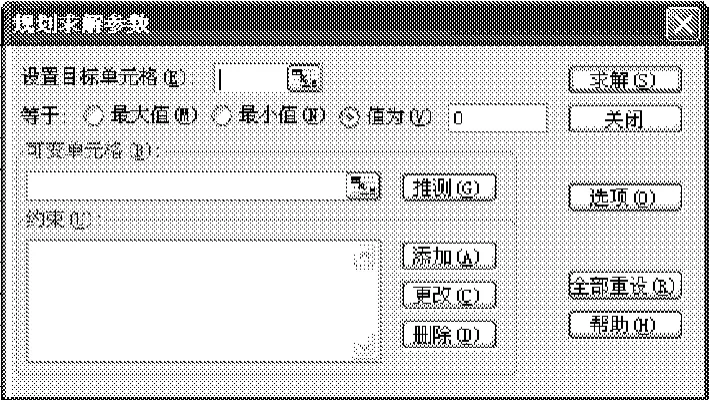
图2 规划求解输入框

一般地,单变量求解能够完成的利用规划求解功能均能实现,而且它也适用于需要同时改变多个单元格中的数值和同时满足某些指定约束条件以获得目标单元格中的指定值的情况[23]。同单变量求解的缺陷有所类似,在求解结果时若单个未知量有多个根,在利用规划求解功能计算时只能得到一个解答,这个解答与初始值有关,但是比单变量求解好在其能够在约束中限定约束条件以更好地得到需要的结果,这样可以避免初始值选取时可能造成的差错。文献[26]简要介绍了利用Excel规划求解工具求解水跃中的共轭水深和圆形断面渠道临界水深等水力计算问题,指出规划求解工具求解的优越性。

2.4 循环引用迭代计算

除了上述利用填充柄以及单变量求解和规划求解工具,利用Excel本身可以完成自动循环引用迭代,这样可以避免利用上述3种求解方法在计算新的案例需要重新计算的麻烦,只要更改实际中的相关量值,计算结果可以相应直接求得。当然,隐式计算式一般难以实现上述的直接计算,需要先通过等式变换成显式迭代公式,然后利用Excel重复计算功能计算所得。可以在“工具”下拉菜单中选择“选项”,在“重新计算”中选择“自动重算”,选择“迭代计算”,其中可以设置“最多迭代次数”及“最大误差”,如图3所示。

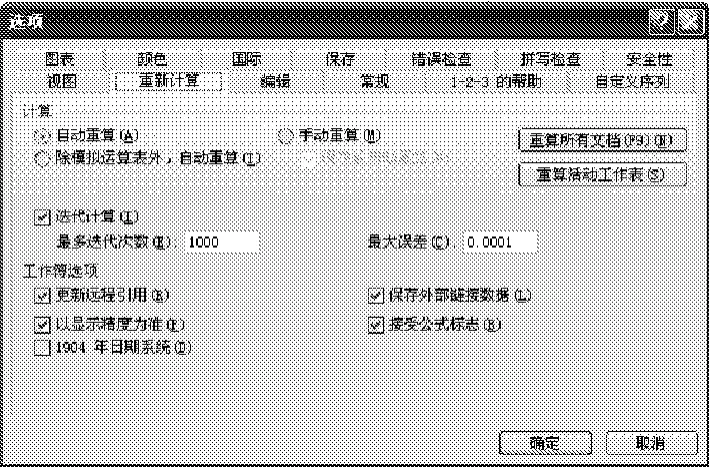
图3 重新计算设置框

Excel中的循环引用只是把被循环引用单元格的初始值作为0处理,因此Excel中的循环引用只能直接处理初始近似为0的迭代计算[27],特别是在共轭水深的计算中往往会受到限制,当然在单变量求解和规划求解也会遇到,只是它们可以利用初始值及约束得到解决。在应用循环引用迭代时需要引用本身的单元格,这样定义的迭代计算与理论上的迭代计算是完全符合的。当然,除了简单迭代法外,还可以使用加速迭代方法[23],常用的有Newton-Raphson法、Aitken法、连续代换法、Wegstein法等。

3 实例分析

3.1 循环引用迭代计算正常水深

有一梯形渠道,已知流量Q=3 m3/s,底坡i=0.0049,粗糙系数n=0.0225,边坡系数m=1.0,渠底宽度b=1 m,求正常水深h0[10]。

根据题意可以利用循环引用迭代进行计算,先将梯形断面正常水深等式变换成显式的迭代计算公式,可参照相关的经典水力学教材[21],由梯形断面水力要素和式(1)得简单迭代式:

先在Excel工作表中设置计算精度,可以在如图3 中进行选择 。在A1、A2、A3、A4、A5、A6、A7、A8、A9分别输入相关的说明和注释以方便阅读,在B3、B4、B5、B6、B7 分别输入已知参数,如图 4 所示。现在需要计算正常水深h0,在B9中输入“=(B3*B5/SQRT(B4))^(3/5)*(B7+2*B9*SQRT(1+B6^2))^(2/5)/(B7+B6*B9)”,由于B9单元格中的计算公式引用了自身单元格,所以可以进行迭代计算,实现自动运算从而求得所需要的结果,最后通过该方法计算所得的正常水深h0=0.8613 m,如下图4,与文献[10]计算结果相一致,完全符合精确解答,如果需要调整计算结果的显示精度,只需在单元格格式的“数字”中设置数值的小数位数。

图4 梯形渠道正常水深循环引用迭代计算

该方法的优点是更改相关的计算参数,结果可以自动计算所得,不需要再进行重复的操作,如果更改过水流量为5 m3/s,10 m3/s,15 m3/s,20 m3/s,可以很方便地直接得到相应的正常水深为1.1117 m,1.5495 m,1.8688 m,2.1285 m,其它的参数变化也能够方便地获得。

3.2 单变量求解临界水深

某工程引水隧洞的设计直径分别为15 m和3 m,对应的设计过水流量分别为500 m3/s和8 m3/s,试计算洞内的临界水深值[8]。

与循环引用迭代计算正常水深一样,先输入相关的说明和已知参数,如图5所示。

图5 圆形断面临界水深单变量求解

3.3 规划求解收缩水深

已知坝(闸)前断面总水头E0=12 m,通过流量Q=200 m3/s,圆形断面直径d=15 m,流速系数 φ=0.95,求坝(闸)后断面收缩水深[9]。

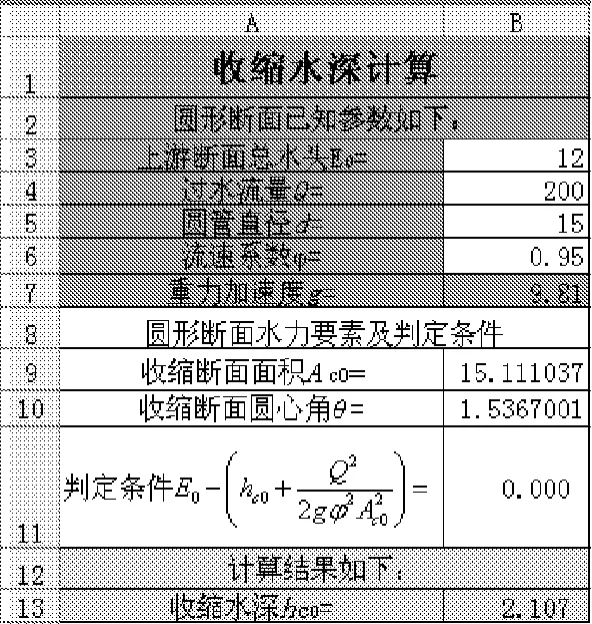
图6 圆形断面收缩水深规划求解

3.4 拖动填充柄计算共轭水深

已知梯形渠道底宽b=2 m,边坡系数m=1.5,流量Q=10 m3/s,第一共轭水深h1=0.25 m,求第二共轭水深h2[7]。

利用拖动填充柄是最先被采用的方法,相应的参数和说明见图7,由于hc1和hc2表示跃前和跃后过水断面形心点的水深,并不等于第一共轭水深h1和第二共轭水深h2,因此先将其进行水深间的转换,可以得到梯形渠道的水跃函数[7]:

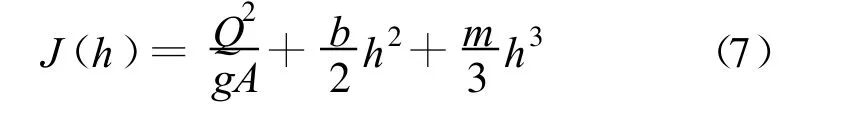
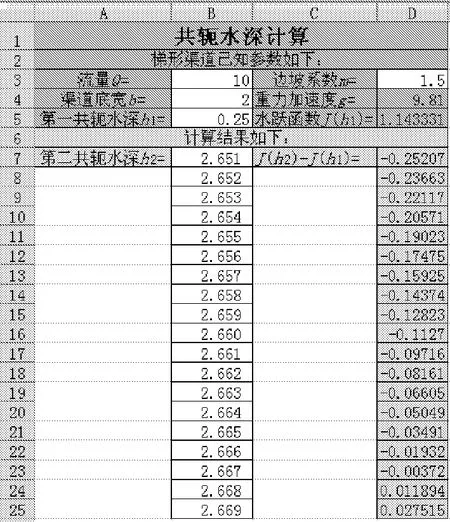
图7 梯形渠道共轭水深拖动填充柄计算

在D5中输入“=＄B＄3^2/＄D＄4*(1/(＄B＄4+＄D＄3*B5)*B5)+＄B＄4/2*B5^2+＄D＄3/3*B5^3”,在共轭水深求解中以J(h2)-J(h1)作为判定条件,因此在D7中输入“=＄B＄3^2/＄D＄4*(1/((＄B＄4+＄D＄3*B7)*B7)-1/((＄B＄4+＄D＄3*＄B＄5)*＄B＄5))+＄B＄4/2*(B7^2-＄B＄5^2)+＄D＄3/3*(B7^3-＄B＄5^3)”,利用填充柄拖动单元格B7和D7往下拉,可以利用判定条件判定解答的范围,然后逐步缩减直至最后得到相应精度的解,可以得到第二共轭水深为2.667 m,与文献[7]一致。当然这种方法如果逐步缩减范围工作量比较大,可以小精度拖动,只是所需单元格数比较多。总体上来说,这种方法比较容易理解,其实质就是人工的试算法,但由于手动操作比较多,本文并不推荐该方法,共轭水深也完全也可以利用其它的方法进行计算,结果依然一致。

4 结 论

从上述的4个算例中可以看出本文介绍的4种Excel计算方法完全可以很好地应用在明渠特征水深的求解中,其精度完全符合工程需求,比起利用编程语言编写求解程序和利用数值计算软件求解计算来说更为方便和简单。除了上述的求解方法,Excel还可以实现图解法等进行计算,这在水力学计算中也可以得到很好的应用。Excel求解明渠特征水深能简化求解计算的过程,减少了工作量,对水力相关参数的修改便捷,大大降低了设计人员的劳动强度,提高计算速度和工作效率。

[1]芦 琴.明渠特征水深直接计算方法的研究[D].杨凌:西北农林科技大学,2005.

[2]李 蕊.梯形明渠特征水深直接计算方法研究[D].杨凌:西北农林科技大学,2008.

[3]葛节忠,王成现.几个常用断面明渠均匀流水深和临界水深的迭代算法[J].华北水利水电学院学报,2006,27(4):33-36.

[4]张宽地,吕宏兴,赵延风.明流条件下圆形隧洞正常水深与临界水深的直接计算[J].农业工程学报,2009,25(3):1-5.

[5]吕宏兴,把多铎,宋松柏.无压流圆形断面水力计算的迭代法[J].长江科学院院报,2003,20(5):15-17.

[6]刘计良,王正中,苏德慧,等.典型断面渠道临界水深计算[J].排灌机械工程学报,2012,30(2):181-187.

[7]赵延风,王正中,芦 琴,等.梯形明渠水跃共轭水深的直接计算方法[J].山东大学学报(工学版),2009,39(2):131-136,150.

[8]刘 刚,滕 凯.圆形断面临界水深简化近似计算方法[J].水利与建筑工程学报,2011,9(6):81-83.

[9]赵延风,王正中,孟秦倩.无压流圆形断面收缩水深的近似计算公式[J].三峡大学学报(自然科学版),2009,31(1):6-8.

[10]赵延风,祝晗英,王正中,等.梯形明渠正常水深的直接计算方法[J].西北农林科技大学学报(自然科学版),2009,37(4):220-224.

[11]许延生,于锋学,陈 瑛.基于牛顿法的梯形明渠临界水深直接算法[J].水动力学研究与进展(A辑),2003,18(4):455-458.

[12]金菊良,丁 晶,杨晓华,等.计算溢流坝下游收缩断面水深的方法[J].水利水电技术,2001,32(3):19-21.

[13]张宽地,吕宏兴,王正中,等.用模式搜索算法求解梯形明渠正常水深[J].长江科学院院报,2009,26(9):25-28,34.

[14]张宽地,王光谦,吕宏兴,等.基于改进粒子群算法求解马蹄形断面正常水深[J].排灌机械工程学报,2011,29(1):54-60.

[15]陈应华,袁晓辉,袁艳斌.粒子群优化在临界水深计算中的应用[J].水电能源科学,2006,24(1):55-57.

[16]李荣东,杨 娜.蚁群算法在泄水建筑物下游收缩断面水深计算中的应用[J].黑龙江水利科技,2008,36(2):47-48.

[17]蔡德所,陶俊波,邱 飞,等.临界水深非线性优化计算的新算法[J].广西大学学报(自然科学版),2007,32(3):238-242.

[18]宁少宇,门宝辉,付 强.计算机算法在求解复杂水力学公式中的应用[J].水利科技与经济,2001,7(4):148-149.

[19]赵延风,王正中,许景辉,等.Matlab语言在梯形明渠水力计算中的应用[J].节水灌溉,2008,(4):38-40,47.

[20]杨茂松,汪 清,马子普.基于MATLAB的常见断面收缩水深的计算方法[J].黑龙江水利科技,2012,(1):54-56.

[21]吴持恭.水力学(第四版)[M].北京:高等教育出版社,2007.

[22]田 静.Excel软件在高职渠道水力参数教学中的应用[J].黄河水利职业技术学院学报,2011,23(2):65-68.

[23]郑立辉,范国枝,韦一良,等.用 Excel求解迭代问题[J].计算机与应用化学,2008,25(11):1429-1431.

[24]雷丰泽,史香玲.用Microsoft Excel单变量求解进行明渠均匀流水力计算初探[J].水利科技与经济,2011,17(11):100-101.

[25]杨 艳.Excel在《水力学》教学过程中的应用[J].长江工程职业技术学院院报,2011,28(3):69-71.

[26]徐文秀.Excel规划求解工具在水力计算中的应用[J].南昌工程学院学报,2008,27(1):30-32,53.

[27]杨明波,卢建立,杨 敏.利用Excel的循环引用自动完成迭代计算[J].计算机应用与软件,2008,25(12):103-105.

Realization for Calculation on Characteristical Depth of Open Channel by Excel

DING Li-ze1,OUYANG Ming2,ZHANG Qing-wen1
(1.Jiaxing Vocational and Technical College,Jiaxing,Zhejiang314036,China;2.College of Architectural Engineering,Zhejiang Polytechnical University,Hangzhou,Zhejiang310014,China)

The four kinds of characteristical depths of open channel,i.e.,normal water depth,critical water depth,contracted water depth and conjugate water depth,can be calculated by the four methods with Microsoft Excel such as filling handle,single goal seeking function,and iteration solving by circulating citation and programming solving function.Through the application examples and comparing with the reference results,it is shown that the depths in various kinds of sections can be obtained by Excel more quickly,precisely and conveniently compared with the general methods,such as manual calculation or computer programming.The process of calculation is simple and can be understood easily,the result of calculation is exact and reliable,and the good methods and new ways of thinking can be provided for teaching and design.

open channel;characteristical depth;Excel;high-exponent formula

TV133

A

1672—1144(2013)02—0176—06

2012-09-11

2012-10-27

丁丽泽(1987—),女,浙江嘉兴人,硕士,主要从事建筑设计及岩土工程的教学和研究。